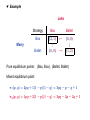
Download Example John Strategy Box Ballet Box (2, 1) ← (0, 0) Marry

☛ Example
John
Strategy
Box
Box
(2, 1)
↑
(0, 0)
Marry
Ballet
Ballet
←
→
(0, 0)
↓
(1, 2)
Pure equilibrium points: (Box, Box), (Ballet, Ballet)
Mixed equilibrium point:
π1 (p, q) = 2pq + 1(1 − p)(1 − q) = 3pq − p − q + 1
π2 (p, q) = 1pq + 2(1 − p)(1 − q) = 3pq − 2p − 2q + 1
1
π1 (p, q) = p(3q − 1) − q + 1,
π2 (p, q) = q(3p − 2) − 2p + 1
Reaction curves:
R1 (q) =







0
h0, 1i
1
. . . q ∈ h0, 31 )
... q =
... q ∈
1
3
( 13 , 1i
R2 (p) =







0
. . . p ∈ h0, 23 )
h0, 1i
... p =
1
... p ∈
2
3
( 23 , 1i
2
Strategy
Box
Box
(2, 1)
Ballet
(0, 0)
Ballet
(0, 0)
(1, 2)
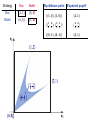
Equilibrium point
Expected payoff
((1, 0), (1, 0))
( 13 , 23 ), ( 23 , 13 )
(2, 1)
2 2
,
3 3
((0, 1), (0, 1))
(2, 1)
3
BIMATRIX GAME
Player 2
Player 1



A=

Strategy
t1
t2
...
tn
s1
(a11 , b11 )
(a12 , b12 )
...
(a1n , b1n )
s2
..
.
(a21 , b21 )
(a22 , b22 )
...
(a2n , b2n )
..............................................
sm
(am1 , bm1 )
a11 a12 . . . a1n
a21 a22 . . . a2n
......................
am1 am2 . . . amn



,

(am2 , bm2 )



B=

...
(amn , bmn )
b11 b12 . . . b1n
b21 b22 . . . b2n
.....................
bm1 bm2 . . . bmn





4
TWO-PLAYER COOPERATIVE GAMES
Definition. Let G be a two-player bimatrix game with m × n
payoff matrices A, B. A joint strategy is an m × n probability matrix P = (pij ). Thus
pij ≥ 0
for
1 ≤ i ≤ m, 1 ≤ j ≤ n,
m X
n
X
pij = 1.
i=1 j=1
Thus, a joint strategy assigns a probability to each pair of pure
strategies. The expected payoff to the row player due to the joint
strategy P is
u(P ) =
m X
n
X
i=1 j=1
pij aij ,
v(P ) =
m X
n
X
pij bij
i=1 j=1
5
☛ Example
In the Battle of the buddies game: a joint strategy is e.g. a matrix


P =
1
2
1
8
1
8
1
4

Expected payoff of Marry:
u(P ) =
1
2
·2+
1
8
·0+
1
8
·0+
1
4
·1=
5
4
Expected payoff of John:
v(P ) =
1
2
·1+
1
8
·0+
1
8
·0+
1
4
·2=1
In a cooperative game the players are allowed to make an agreement about which joint strategy to choose.
6
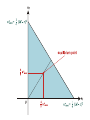
Definition. Cooperative payoff region is the set
K = {(u(P ), v(P )) : P is a joint strategy}.
(1)
K is convex, closed and bounded set, which contains the corresponding non-cooperative payoff region Π = {(u(p, q), v(p, q))}.
7
CONVEX SETS
Definition. A set M ⊂ Rn is called convex if, for every
x, y ∈ M and every real number t, 0 ≤ t ≤ 1, it is:
tx + (1 − t)y ∈ M
8
In other words, the set M is convex, if every line segment whose
end-points are in M lies entirely in M.
Definition. Let F = {x1 , x2 , . . . , xk } be a finite subset of
Rn . A convex combination of the set F is defined as a
vector
w=
k
X
ti xi ,
where t1 ≥ 0, . . . , tk ≥ 0,
t1 +· · · tk = 1.
i=1
By induction, if a given set M is convex, then each convex combination of its points lies again in M.
Definition. Let A be a subset of Rn . Convex hull of the set
A is defined as the set of all convex combinations of finite
subsets of the set A. For the convex hull we will use the
symbol conv(A).
9
Prove that the convex hull is a convex set and every convex set
containing A contains conv(A), too.
Theorem. Let G be a two-player game given by an m×n bimatrix
C. Cooperative payoff region is the convex hull of the set of points
in R2 whose coordinates are the elements of the bimatrix C.
Proof. If P is a joint strategy, then the corresponding payoff pairs
are
m X
n
X
(u(P ), v(P )) =
pij cij .
i=1 j=1
All these points form a convex hull of the set
{cij , 1 ≤ i ≤ m, 1 ≤ j ≤ n}.
Conversely, any point of the convex hull of this set is a payoff pair.
10
Definition. The set S ⊂ R2 is called symmetric if, for every
u, v ∈ R it is:
(v, u) ∈ S ⇐⇒ (u, v) ∈ S.
Definition. Consider a set A ⊂ R2 . The symmetric convex
hull of A is defined to be the convex hull of the set
A ∪ {(v, u) : (u, v) ∈ A}.
It is denoted sconv(A).
Assertion. Let A ⊂ R2 and k is such a number that for every
point (u, v) ∈ A we have: u + v ≤ k. Then the same inequality
holds for every point of the symmetric convex hull sconv(A).
11
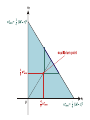
BARGAINING PROBLEM
Definition. Bargaining problem is an ordered pair (P, u),
where P is a cooperative payoff region, u0 = (u0 , v0 ),
where u0 , v0 are the payoffs in the case of a disagreement
(”threats”).
12
Definition. The payoff pair (û, v̂) ∈ P is called Pareto
optimal or non-dominated if there does not exist any other
payoff pair (u, v) ∈ P for which
u ≥ û
and
v ≥ v̂,
withal at least one inequality is strict.
13
Definition. The bargaining set for two-player cooperative
game is the set of all Pareto optimal payoff pairs (u, v) ∈ P
such that
u ≥ v1 ,
v ≥ v2 ,
where v1 , v2 are the maximin values, i.e.
v1 = max min u(p, q),
p
q
v2 = max min v(p, q)
q
p
14
Antoine Augustin Cournot (1801 – 1877)
1838 Recherches sur les principes mathématiques de la théorie des richesses
15
16
17
18
JOHN FORBES NASH (*1928)
1950 The bargaining problem, Econometrica 18
1953 Two-person cooperative games, Econometrica 21
19
Nash bargaining axioms
Consider a bargaining problem (P, (u0 , v0 )), denote its
solution Ψ(P, (u0 , v0 )) = (u∗ , v ∗ ).
20
Axiom 1 (Individual rationality)
u∗ ≥ u0 , v ∗ ≥ v0
21
Axiom 2 (Pareto Optimality)
The pair (u∗ , v ∗ ) is Pareto optimal.
22
Axiom 3 (Feasibility)
(u∗ , v ∗ ) ∈ P.
23
Axiom 4 (Independence of Irrelevant Alternatives)
If P0 is a payoff region contained in P and both pairs
(u0 , v0 ), (u∗ , v ∗ ) ∈ P0 , then
Ψ(P0 , (u0 , v0 )) = (u∗ , v ∗ ).
24
Axiom 5
(Independence under Linear Transformations)
Suppose P0 is obtained from P by the linear transformation
u0 = au + b,
v 0 = cv + d,
where
a, c > 0,
then
Ψ(P0 , (au0 + b, cv0 + d)) = (au∗ + b, cv ∗ + d).
Axiom 6 (Symmetry)
Suppose that P is symmetric [(u, v) ∈ P ⇔ (v, u) ∈ P]
and (u0 , v0 ) ∈ P, then u∗ = v ∗ .
25
Theorem. There exists a unique arbitration procedure Ψ
satisfying Nash’s axioms.
Proof.
• Construction of Ψ
Case (i) There exists (u, v) ∈ P such that u > u0 and v > v0 .
Let K be the set of all such points (u, v). Define
g(u, v) = (u − u0 )(v − v0 ),
for
(u, v) ∈ K.
It can be proved that there exists a unique point (u∗ , v ∗ ) in which
the function g(u, v) attains its maximum value. Define
Ψ(P, (u0 , v0 )) = (u∗ , v ∗ ).
Define
Ψ(P, (u0 , v0 )) = (u∗ , v ∗ ).
26
Case (ii) No (u, v) ∈ P exists such that u > u0 and v > v0 .
Consider the following three subcases:
Case (iia) There exists (u0 , v) ∈ P such that v > v0 .
27
The largest v with this property for which it is (u0 , v) ∈ P
denote v ∗ .
Define
Ψ(P, (u0 , v0 )) = (u0 , v ∗ ).
Case (iib) There exists (u, v0 ) ∈ P such that u > u0 .
The largest u with this property for which it is (u, v0 ) ∈ P
denote u∗ .
Define
Ψ(P, (u0 , v0 )) = (u∗ , v0 ).
Case (iic) Neither (iia) nor (iib) is true.
Define
Ψ(P, (u0 , v0 )) = (u0 , v0 ).
28
Cases (iia) and (iib) can not both be true: suppose that they are
and define
1
1
(u0 , v 0 ) = (u0 , v) + (u, v0 ).
2
2
0
0
Then (u , v ) is in P (from convexity) and satisfies the condition
of Case (i) – since Case (i) does not hold, this is a contradiction.
• Verifying Nash Axioms
Axioms 1 and 3 apparently hold in all cases.
29
Axiom 2 (Pareto Optimality): By contradiction: suppose that
(u, v) ∈ P exists that dominates the point (u∗ , v ∗ ) and is different
from it.
In Case (i) it would be
(u − u0 ) ≥ (u∗ − u0 ),
(v − v0 ) ≥ (v ∗ − v0 )
and at least one of these inequalities would be strict (since (u, v) 6=
(u∗ , v ∗ )). Thus,
g(u, v) > g(u∗ , v ∗ ),
which is a contradiction to the construction of (u∗ , v ∗ ).
In Case (iia) it must be u∗ = u0 = u because (iib) does not hold.
It is therefore v > v ∗ , which contradicts to the definition of v ∗ .
In Case (iib) we can proceed similarly.
In Case (iic) we have (u∗ , v ∗ ) = (u0 , v0 ); if it would be u > u0 ,
then Case (iib) would hold, for v > v0 it would be the Case (iia),
which is again a contradiction.
30
Axiom 4 (Independence of Irrelevant Alternatives):
If P0 is a payoff region contained in P and both pairs
(u0 , v0 ), (u∗ , v ∗ ) ∈ P0 , then
Ψ(P0 , (u0 , v0 )) = (u∗ , v ∗ ).
In case (i) the maximum value of the function g subject to the
constrained K ∩ P0 , is less of equal to its maximum value on the
set K. Since (u∗ , v ∗ ) ∈ P0 , these maximas are equal. Thus,
Ψ(P0 , (u0 , v0 )) = Ψ(P, (u0 , v0 )).
Similarly for other cases.
31
Axiom 5 (Independence under Linear Transformations):
Suppose P0 is obtained from P by the linear transformation
u0 = au + b,
v 0 = cv + d,
where
a, c > 0,
then
Ψ(P0 , (au0 + b, cv0 + d)) = (au∗ + b, cv ∗ + d).
In case (i), the same case holds also for a payoff region P0 with
the status quo point (au0 + b, cv0 + d). Thus,
(u0 − (au0 + b))(v 0 − (cv0 + d)) = ac(u − u0 )(v − v0 ).
Since a, c > 0, the function on the left side attains its maximum
at (au∗ + b, cv ∗ + d). In case (i) the axiom (5) therefore holds.
The process in other cases is similar.
32
Axiom 6 (Symmetry):
If u∗ 6= v ∗ than from the symmetry (v ∗ , u∗ ) ∈ P; in case (i) it
would be
g(v ∗ , u∗ ) = g(u∗ , v ∗ ).
But the function g attains its maximum at a unique point, what is
a contradiction. Due to symmetry, cases (iia) and (iib) can not
occur.
• Uniqueness.
The proof is done by a contradiction resulting from the assumption
that there exists another arbitration procedure Ψ satisfying Nash
axioms. Since these procedures are different, there exists a payoff
region P and „status quo“ point (u0 , v0 ) ∈ P, for which
(u, v) = Ψ(P, (u0 , v0 )) 6= Ψ(P, (u0 , v0 )) = (u∗ , v ∗ ).
33
Assertion. Let P be a payoff region and (u0 , v0 ) ∈ P. Assume
that there exists a point (u, v) ∈ P with
u > u0 ,
v > v0 ;
Denote with K the set of all points (u, v) with the mentioned
property. Define on K a function
g(u, v) = (u − u0 )(v − v0 ).
Then g attains its maximum on K at one and only one point.
34
Ehud Kalai, Meir Smorodinsky
Other Solutions to Nash’s Bargaining Problem, 1975
(Econometrica 43, 513–518)
Solution arising from the most optimistic expectations:
35
Instead of the condition 4 (independence of irrelevant alternatives):
Individual monotonicity: If P ⊆ P0 and for j 6= i it is
aj (P0 ) = aj (P), then Ki (P, d) ≤ Ki (P0 , d).
36
Theorem. Kalai-Smorodinsky’s solution is the only solution satisfying the conditions of pareto optimality, symmetry, independence
of linear transformations and individual monotonicity (n = 2).
37
Egalitarian solution – Ehud Kalai, 1977
Strong monotonicity: If P ⊆ P0 , then Ki (P, d) ≤
Ki (P0 , d) for all i.
Theorem. Egalitarian solution is the only solution satisfying wak
Pareto-optimality, symmetry, and strong monotonicity.
38
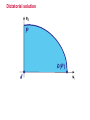
Dictatorial solution
39
☛ Example. Consider a cooperative game with a bimatrix
(2, −1) (−2, 1) (1, 1)
.
(−1, 2) (0, 2) (1, −2)
(2)
Maximin values: v1 = − 25 , v2 = 1.
40
Set (u0 , v0 ) = (− 25 , 1). Arbitration point must be found among
the points of the payoff function that dominate the point (− 25 , 1)
but that are not dominated by any other points – i.e. in this case
on the line-segment with end-points (0, 2) and (1, 1) which represents the bargaining set. According to the construction of the
arbitration point we search the maximum of the function
2
g(u, v) = (u − u0 )(v − v0 ) = u +
(v − 1)
5
in the line segment given by an equality v = −u + 2. Thus, the
only problem is to find the extreme of the function of one unknown.
3
2
2
g(u, −u + 2) = u +
(−u + 1) = −u2 + u + .
5
5
5
With help of a simple calculus we obtain
u=
3
10
,
v=
17
10
.
41
☛ Example. Consider a cooperative game with a bimatrix
(5, 1) (7, 4) (1, 10)
.
(1, 1) (9, −2) (5, 1)
(3)
Maximin values are v1 = 3, v2 = 1. Bargaining set consists of
two line segments; apply the process from the previous example
for both segments. For one line segment, maximum lies out of it
and for the second one we obtain an arbitration point
u=
13
2
,
v=
9
2
.
42