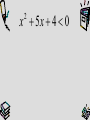* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download terms - Catawba County Schools
List of important publications in mathematics wikipedia , lookup
Proofs of Fermat's little theorem wikipedia , lookup
Mathematics of radio engineering wikipedia , lookup
Recurrence relation wikipedia , lookup
Horner's method wikipedia , lookup
Factorization of polynomials over finite fields wikipedia , lookup
Elementary mathematics wikipedia , lookup
Vincent's theorem wikipedia , lookup
Chapter 6 Polynomials and Polynomial Functions In this chapter, you will … Learn to write and graph polynomial functions and to solve polynomial equations. Learn to use important theorems about the number of solutions to polynomial equations. Learn to solve problems involving permutations, combinations and binomial probability. 6-1 Polynomial Functions What you’ll learn … To classify polynomials To model data with polynomial functions 2.04 Create and use best-fit mathematical models of linear, exponential, and quadratic functions to solve problems involving sets of data. a. Interpret the constants, coefficients, and bases in the context of the data. b. Check the model for goodness-of-fit and use the model, where appropriate, to draw conclusions or make predictions. 2.06 Use cubic equations to model and solve problems. a. Solve using tables and graphs. b. Interpret constants and coefficients in the context of the problem. A monomial is an expression that is a real number, a variable or a product of real numbers and variables. 13, 3x, -57, x², 4y², -2xy, or 520x²y² A binomial is the sum of two monomials. It has two unlike terms. 3x + 1, x² - 4x, 2x + y, or y - y² A trinomial is the sum of three monomials. It has three unlike terms. x2 + 2x + 1, 3x² - 4x + 10, 2x + 3y + 2 A polynomial is the sum of one or more terms. x2 + 2x, 3x3 + x² + 5x + 6, 4x - 6y + 8 • The exponent of the variable in a term determines the degree of that term. • The terms in the polynomial are in descending order by degree. • This order demonstrates the standard form of a polynomial. 3 Leading Coefficient Cubic Term 2 Quadratic Term Linear Term Constant Term Degree Name Using Degree Polynomial Example Number of Terms Name Using Number of Terms 0 Constant 6 1 monomial 1 Linear x+3 2 binomial 2 Quadratic 3x2 1 monomial 3 Cubic 2x3 -5x2 -2x 3 trinomial 4 Quartic x4 + 3x2 2 binomial 5 Quintic -2x5+3x2-x+4 4 polynomial Example 1 Classifying Polynomials Write each in standard form and classify it by degree and number of terms. -7x + 5x4 x2 – 4x + 3x3 +2x 4x – 6x + 5 Linear Model Quadratic Model Cubic Model Example 2 Comparing Models Using a graphing calculator, determine whether a linear model, a quadratic model, or a cubic model best fits the values in the table. x 0 5 10 15 20 y 10.1 2.8 8.1 16.0 17.8 Example p.303 #17 The data at the right indicate that the life expectancy for residents of the US has been increasing. a. Find a quadratic model for the data set. b. Find a cubic model for the data set. c. Graph each model. Compare the quadratic and cubic models to determine which one is a better fit. Year of Birth Males Females 1970 67.1 74.7 1980 70.0 77.4 1990 71.8 78.8 2000 73.2 80.2 2010 74.5 81.3 Example p.303 #23 Find a cubic model for each function. Then use your model to estimate the value of y when x=17. X 0 2 4 6 8 10 12 14 16 18 20 Y 4.1 6 15.7 21.1 23.6 23.1 24.7 24.9 23.9 25.2 29.5 Example p.304 #31 h=10 The diagram shows a cologne bottle that consists of a cylindrical base and a hemispherical top. a. Write an expression for the cylinder’s volume. b. Write an expression for the volume of the hemispherical top. r c. Write a polynomial to represent the total volume 6-2 Polynomials and Linear Factors What you’ll learn … To analyze the factored form of a polynomial To write a polynomial function from its zeros 1.03 Operate with algebraic expressions (polynomial, rational, complex fractions) to solve problems. Example 1 Writing a Polynomial in Standard Form Write the expression (x+1)(x+2)(x+3) as a polynomial in standard form. Write the expression (x+1)(x+1)(x+2) as a polynomial in standard form. Example 2 Writing a Polynomial in Factored Form Write 2x3 +10x2 + 12x in factored form. Write 3x3 - 3x2 - 36x in factored form. Example 3 Real World Connection Several popular models of a. carry-on luggage have a length 10 in. greater than their depth. To comply with airline regulations, b. the sum of the length, width and depth may not c. exceed 40 in. Assume that the sum of the length, width and depth is 40 in. Graph the function relating volume V to depth x. Describe a realistic domain. What is the maximum possible volume of a piece of luggage? What are the corresponding dimensions of the luggage? The maximum value in Example 3 is the greatest value of the points in a region of the graph. It is called a relative maximum. Similarly, a relative minimum is the least y-value among nearby points on a graph. Relative maximum Value of y x intercepts Relative minimum Value of y Example 4 Finding Zeros of a Polynomial Function Find the zeros of y= (x-2)(x+1)(x+3). Then graph the function. Find the zeros of y= (x-7)(x-5)(x-3). Then graph the function. You can reverse the process and write linear factors when you know the zeros. The relationship between the linear factors of a polynomial and the zeros of a polynomial is described by the Factor Theorem. Factor Theorem The expression x-a is a linear factor of a polynomial if and only if the value a is a zero of the related polynomial function. Example 5 Writing a Polynomial Function From Its Zeros Write a polynomial function in standard form with zeros at -2, 3, and 3. Write a polynomial function in standard form with zeros at -4, -2, and 1. While the polynomial function in Example 5 has three zeros, it has only two distinct zeros: -2 and 3. If a linear factor of a polynomial is repeated, then the zero is repeated. A repeated zero is called a multiple zero. A multiple zero has a multiplicity equal to the number of times the zero occurs. In example 5 the zero 3 has a multiplicity of 2. Example 6 Finding the Multiplicity of a Zero Find any multiple zeros of f(x)=x4 +6x3+8x2 and state the multiplicity. Find any multiple zeros of f(x)=x3 - 4x2+4x and state the multiplicity. Equivalent Statements about Polynomials 1. -4 is a solution of x2 +3x -4 =0. 2. -4 is an x-intercept of the graph of y= x2 +3x -4. 3. -4 is a zero of y= x2 +3x -4. 4. x+4 is a factor of x2 +3x -4. 6-3 Dividing Polynomials What you’ll learn … To divide polynomials using long division To divide polynomials using synthetic division 1.03 Operate with algebraic expressions (polynomial, rational, complex fractions) to solve problems. You can use polynomial division to help find all the zeros of a polynomial function. Division of polynomials is similar to numerical long division. 8 56 217 65465 x 2 2x Example 1a Polynomial Long Division Divide x2 +3x – 12 by x - 3 Example 1b Polynomial Long Division Divide x2 -3x + 1 by x - 4 Example 2 Checking Factors Determine whether x+4 is a factor of each polynomial x2 + 6x + 8 x3 + 3x2 -6x - 7 To check (divisor) (quotient) + r = dividend To divide by a linear factor, you can use a simplified process that is known as synthetic division. In synthetic division, you omit all variables and exponents. By reversing the sign in the divisor, you can add throughout the process instead of subtracting. Example 3a Using Synthetic Division Use synthetic division to divide 3x3 – 4x2 +2x – 1 by x +1 Example 3b Using Synthetic Division Use synthetic division to divide x3 + 4x2 + x – 6 by x +1 Example 4 Real World Connection The volume in cubic feet of a sarcophagus (excluding the cover) can be expressed as the product of its three dimensions: V(x) = x3 – 13x + 12. The length is x + 4. a. Find linear expressions with integer coefficients for the other dimensions. Assume that the width is greater than the height. Check for Understanding Use synthetic division to divide x3 - 2x2 - 5x + 6 by x + 2 Remainder Theorem If a polynomial P(x) of degree n>1 is divided by (x-a). Where a is a constant, then the remainder is P(a). Example 5a Evaluating a Polynomial by Synthetic Division Use synthetic division to find P(-4) for P(x) = x4 - 5x2 + 4x + 12 Example 5b Evaluating a Polynomial by Synthetic Division Use synthetic division to find P(-1) for P(x) = 2x4 + 6x3 – x2 - 60 6-4 Solving Polynomial Equations What you’ll learn … To solve polynomials equations by graphing To solve polynomials equations by factoring 1.03 Operate with algebraic expressions (polynomial, rational, complex fractions) to solve problems. Example 1 Solving by Graphing Steps Graph y1= x3 + 3x2 Graph y2= x + 3 Use the intersection feature to find the x Solve x3 - 19x = -2x2 + 20 values at the points of intersection. Solve x3 + 3x2 = x + 3 Example 3 Real World Connection The dimensions in inches of a portable kennel can be expressed as width x, length x+7 and height x-1. The volume is 5.9 ft3. Find the portable kennel’s dimensions. Sometimes you can solve polynomial equations by factoring the polynomial and using the factor Theorem. Recall that a quadratic expression that is the difference of squares has a special factoring pattern. Similarly, a cubic expression may be the sum of cubes or the difference of cubes. Sum and Differences of Cubes a3 + b3 = (a + b)(a2 – ab + b2) a3 - b3 = (a - b)(a2 + ab + b2) Example 3 Factoring a Sum of Cubes Factor 8x3 + 1 Factor 64x3 + 27 Example 3 Factoring a Difference of Cubes Factor 8x3 - 27 Factor 125x3 - 64 Example 4 Solving a Polynomial Equation Factor x3 + 8 = 0 Factor 27x3 + 1 Example 5 Factoring by Using a Quadratic Form Factor x4 - 2x2 – 8 = 0 Factor x4 + 7x2 + 6 = 0 6-5 Theorems About Roots of Polynomial Equations What you’ll learn … To solve equations using the Rational Root Theorem To use the Irrational Root Theorem and the Imaginary Root Theorem 1.02 Define and compute with complex numbers. 1.03 Operate with algebraic expressions (polynomial, rational, complex fractions) to solve problems. Consider the equivalent equations…. x3 – 5x2 -2x +24 = 0 and (x+2)(x-3)(x-4) =0 -2, 3 and 4 are the roots of the equation. • The product of -2,3 and 4 is 24. • Notice that all the roots are factors of the constant term 24. • In general, if the coefficients in a polynomial equation are integers, then any integer root of the equation is a factor of the constant term. Both the constant and the leading coefficient of a polynomial can play a key role in identifying the rational roots of the related polynomial equation. The role is expressed in the Rational Root Theorem. p If q is in simplest form and is a rational root of the polynomial equation with integer coefficients, then p must be a factor of the constant term and q must be a factor of the leading coefficient. Example 1a Finding Rational Roots x3 - 4x2 - 2x + 8 = 0 1. 2. Steps List the possible rational roots of the leading coefficient and the constant. Test each possible root. Example 1b Finding Rational Roots 2x3 - x2 +2x - 1 = 0 1. 2. Steps List the possible rational roots of the leading coefficient and the constant. Test each possible root. Example 1c Finding Rational Roots x3 - 2x2 - 5x + 10 = 0 1. 2. Steps List the possible rational roots of the leading coefficient and the constant. Test each possible root. Example 1d Finding Rational Roots 3x3 + x2 -x+1=0 1. 2. Steps List the possible rational roots of the leading coefficient and the constant. Test each possible root. In Chapter 5 you learned to find irrational solutions to quadratic equations. For example, by the Quadratic Formula, the solutions of x2 – 4x -1 =0 are 2+√5 and 2 - √5. Number pairs of the form a+√b and a-√b are called conjugates. You can often use conjugates to find the irrational roots of a polynomial equation. Irrational Root Theorem Let a and b be rational numbers and let √b be an irrational number. If a+ √b is a root of a polynomial equation with rational coefficients, then the conjugate a- √b also is a root. Example 3 Finding Irrational Roots A polynomial equation with integer coefficients has the following roots. Find two additional roots.. 1 + √3 and -√11 2 - √7 and √5 Number pairs of the form a+bi and a-bi are complex conjugates. You can use complex conjugates to find an equation’s imaginary roots. Imaginary Root Theorem If the imaginary number a+bi is a root of a polynomial equation with real coefficients then the conjugate a-bi also is a root. Example 4 Finding Imaginary Roots A polynomial equation with integer coefficients has the following roots. Find two additional roots.. 3i and -2 + i 3 - i and 2i Example 5a Writing a Polynomial Equation from its Roots Find a third degree polynomial equation with rational coefficients that has roots -1 and 2-i. 1. 2. 3. Steps Find the other root using the Imaginary Root Theorem. Write the factored form of the polynomial using the Factor Theorem. Multiply the factors. Example 5b Writing a Polynomial Equation from its Roots Find a third degree polynomial equation with rational coefficients that has roots 3 and 1+i. 1. 2. 3. Steps Find the other root using the Imaginary Root Theorem. Write the factored form of the polynomial using the Factor Theorem. Multiply the factors. Example 5c Writing a Polynomial Equation from its Roots Find a fourth degree polynomial equation with rational coefficients that has roots i and 2i. 1. 2. 3. Steps Find the other root using the Imaginary Root Theorem. Write the factored form of the polynomial using the Factor Theorem. Multiply the factors. 6-6 The Fundamental Theorem of Algebra What you’ll learn … To use the Fundamental Theorem of Algebra in solving polynomial equations with complex roots 1.02 Define and compute with complex numbers. 1.03 Operate with algebraic expressions (polynomial, rational, complex fractions) to solve problems. You have solved polynomial equations and found that their roots are included in the set of complex numbers. That is, the roots have been integers, rational numbers, irrational numbers and imaginary numbers. But can all polynomial equations be solved using complex numbers? In 1799, the German mathematician Carl Friedrich Gauss proved that the answer to this question is yes. The roots of every polynomial equation, even those with imaginary coefficients, are complex numbers. Carl Friedrich Gauss The answer is so important that his theorem is called the Fundamental Theorem of Algebra. Fundamental Theorem of Algebra If P(x) is a polynomial of degree n>1 with complex coefficients, then P(x) = 0 has at least one complex root. Corollary Including imaginary roots and multiple roots, an nth degree polynomial equation has exactly n roots; the related polynomial function has exactly n zeros. Example 1a Using the Fundamental Theorem of Algebra Find the number of complex roots, the possible number of real roots and possible number of rational roots. x4 - 3x3 + x2 – x +3 = 0 Example 1b Using the Fundamental Theorem of Algebra Find the number of complex roots, the possible number of real roots and possible number of rational roots. x3 - 2x2 + 4x -8 = 0 Example 1c Using the Fundamental Theorem of Algebra Find the number of complex roots, the possible number of real roots and possible number of rational roots. x5 + 3x4 - x - 3 = 0 6-8 The Binomial Theorem What you’ll learn … To use Pascal’s Triangle To use the Binomial Theorem 1.03 Operate with algebraic expressions (polynomial, rational, complex fractions) to solve problems. You have learned to multiply binomials using the FOIL method and the Distributive Property. If you are raising a single binomial to a power, you have another option for finding the product. Consider the expansion of several binomials. To expand a binomial being raised to a power, first multiply; then write the result as a polynomial in standard form. Pascal’s Triangle (a + b)2 = (a + b) (a + b) a2 + 2ab + b2 The coefficients of the product are 1,2 1. (a + b)3 = (a + b) (a + b) (a + b) a3 + 3a2b + 3ab2 + b3 The coefficients of the product are 1,3,3,1. Pascal’s Triangle Example 1a Using Pascal’s Triangle Expand (a+b)8 Example 1b Using Pascal’s Triangle Expand (x - 2)4 Example 1c Using Pascal’s Triangle Expand (m + 3)5 Example 1d Using Pascal’s Triangle Expand (3 – 2x)6 Quadratic Inequalities Quadratics Before we get started let’s review. A quadratic equation is an equation that can 2 be written in the form ax bx c 0 , where a, b and c are real numbers and a cannot equal zero. In this lesson we are going to discuss quadratic inequalities. Quadratic Inequalities What do they look like? Here are some examples: x 2 3x 7 0 3x 4 x 4 0 2 x 16 2 Quadratic Inequalities When solving inequalities we are trying to find all possible values of the variable which will make the inequality true. Consider the inequality x2 x 6 0 We are trying to find all the values of x for which the quadratic is greater than zero or positive. Solving a quadratic inequality We can find the values where the quadratic equals zero 2 x x6 0 by solving the equation, x 3x 2 0 x 3 0 or x 2 0 x 3 or x 2 Solving a quadratic inequality 2 x x6 0 For the quadratic inequality, we found zeros 3 and –2 by solving the equation x 2 x 6 0. Put these values on a number line and we can see three intervals that we will test in the inequality. We will test one value from each interval. -2 3 Solving a quadratic inequality Interval ,2 Test Point Evaluate in the inequality True/False x2 x 6 0 x 3 32 3 6 9 3 6 6 0 True x2 x 6 0 2, 3 3, x0 02 0 6 0 0 6 6 0 False x2 x 6 0 x4 42 4 6 16 4 6 6 0 True Example 2: 2 2 x 3x 1 0 Solve 2 2 x 3x 1 0 First find the zeros by solving the equation, 2 x 2 3x 1 0 2x 1x 1 0 2 x 1 0 or x 1 0 1 x or x 1 2 Example 2: Now consider the intervals around the zeros and test a value from each interval in the inequality. The intervals can be seen by putting the zeros on a number line. 1/2 1 Example 2: Interval Test Point Evaluate in Inequality True/False 2 x 2 3x 1 0 1 , 2 x0 20 30 1 0 0 1 1 0 2 False 2 x 2 3x 1 0 1 ,1 2 9 9 1 3 3 2 3 1 1 0 8 4 8 4 4 2 3 x 4 True 2 x 2 3x 1 0 1, x2 22 32 1 8 6 1 3 0 2 False Summary In general, when solving quadratic inequalities 1. Find the zeros by solving the equation you get when you replace the inequality symbol with an equals. 2. Find the intervals around the zeros using a number line and test a value from each interval in the number line. 3. The solution is the interval or intervals which make the inequality true. x 5 x 24 0 2 12 x x 0 2 16 x 1 0 2 x 5x 4 0 2 In this chapter, you should have … Learned to write and graph polynomial functions and to solve polynomial equations. Learned to use important theorems about the number of solutions to polynomial equations. Learned to solve problems involving permutations, combinations and binomial probability.