Download Document

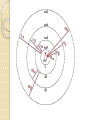
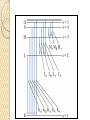
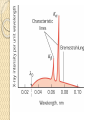
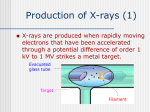
UNIT-IV
X-RAYS
X-RAYS
•
X-rays are
electromagnetic waves
•
Their interaction with
matter is governed
by quantum theory.
•
The energy of x-ray
photons is E = hv.
•
Wavelengths of x-rays
is 0.001 to 10 nm
Discovery of X-Rays

Wilhelm Roentgen (1895)
image from Cathode Ray Tube Site
image from Wolfram Research
High Energy Photons and Matter

Production
◦ Bremsstrahlung Radiation (Continuum)
◦ Atomic and Nuclear Processes (Radioactive Decay)

Fluorescence
–

Characteristic Lines (Inner Shell)
Scatter
–
–
–
Photoelectric Effect (<50 keV)
Compton Scattering (50 keV to 1 MeV)
Pair Production (> 5 MeV)
pair production from the wikipedia commons
Production of X-rays

X-rays are produced when rapidly moving
electrons that have been accelerated through a
potential difference of order 1 kV to 1 MV strikes
a metal target.
Production of X-rays
Electrons from a hot element are accelerated
onto a target anode.
 When the electrons are suddenly decelerated
on impact, some of the kinetic energy is
converted into EM energy, as X-rays.
 Less than 1 % of the energy supplied is
converted into X-radiation during this process.
The rest is converted into the internal energy
of the target.

Intensity of X-Rays
To increase the intensity of x-rays, we need:

to increase the tube current (more
electrons)

to increase tube voltage (increasing the
energy of each x-ray photon).

Under certain tube voltage, the current of
filament control the intensity of x-rays. They
are proportional to each other.
The hardness of x-rays
•
The hardness of x-ray is defined as its
penetrating ability.
•
It depends on the wavelength of the x-rays
not on the number of x-ray photons.
•
The hardness of x-rays is proportional to
the energy of x-ray photons.
•
Energy of x-ray photons is proportional to
the voltage applied to the x-ray tube.
Therefore, the hardness of x-rays is usually
expressed by tube voltage in kV.
Properties of X-rays







X-rays travel in straight lines.
X-rays cannot be deflected by electric field or
magnetic field.
X-rays have a high penetrating power.
Photographic film is blackened by X-rays.
Fluorescent materials glow when X-rays are
directed at them.
Photoelectric emission can be produced by X-rays.
Ionization of a gas results when an X-ray beam is
passed through it.
Uses of X-rays

In medicine
To diagnose illness and for
treatment.


In industry
To locate cracks in metals.
X-ray crystallography
To explore the structure of
materials.
X-RAY SPECTRA

X-rays are emitted from the anode
surface
as
a
consequence
of
bombardment by the electron stream.
Two distinct processes are involved in xray emission:
(1)
Some of the electrons are stopped by
the target
(2)
Others transfer their energy in whole or
in part to the atoms of the target to
excite the atoms.

The latter is the characteristic of the
target, while
the
former
emits
continuous spectrum.
X-ray Spectra
X-ray Spectra

The graph shows the following features
◦ A continuous background of X-radiation in
which the intensity varies smoothly with
wavelength. The background intensity reaches a
maximum value as the wavelength increases,
then the intensity falls at greater wavelengths.
◦ Minimum wavelength which depends on the
tube voltage. The higher the voltage the smaller
the value of the minimum wavelength.
◦ Sharp peaks of intensity occur at wavelengths
unaffected by change of tube voltage.
Continuous X-ray spectrum
The x-rays from its tube usually contains
different wavelengths and the plot of its
intensity versus wavelength for spectrum of
radiation emitted by an x-ray tube is called
x-ray spectrum.
Minimum wavelength in the X-ray Spectra
When an electron hits the target its entire kinetic
energy is converted into a photon.
 The work done on each electron when it is
accelerated onto the anode is eV.
 Hence hf = eV and the maximum frequency

f max
eV

h
Therefore,
min
hc

eV
Characteristic X-ray Spectra
Different target materials give different wavelengths
for the peaks in the X-ray spectra.
 The peaks are due to electrons knock out innershell electrons from target atoms.
 When these inner-shell vacancies are refilled by
free electrons, X-ray photons are emitted.
 The peaks for any target element define its
characteristic X-ray spectrum.

Characteristic X-Ray Spectra
Bohr “shell” hypothesis.
 An electron shell based on the radius rn can
be associated with each of the principle
quantum numbers n.
 Electrons with lower values of n are more
tightly bound to the nucleus than those with
higher values.
 The radii of the orbits increase as n2
 An energy is associated with each value of n

Characteristic X-Ray Spectra
When we add electrons to a fully ionized
many-electron atom, the inner shells (low
values of n) fill up before the outer shells.
 Historically n = 1 is K the shell, n = 2 is
the L shell, n = 3 is the M shell, and so on.

The Characteristic X-Ray Process
Let a high-energy electron in an x-ray tube
collides with an electron in the K shell
(Electrons in the K shell are called K electrons.)
in the target atom.
 If enough energy is transferred to the K
electron to dislodge it from the atom, a vacancy
is left in the K shell.
 The atom is stable in its lowest energy state, or
ground state), so an electron from one of the
higher shells will change its state and fill the
inner shell vacancy at a lower energy.

The Characteristic X-Ray Process
A photon is emitted when the electron
changes state.
 When this occurs in a heavy atom, the
photon that is emitted is in the x-ray
portion of the spectrum.
 E (x-ray) = Eu - El

Moseley’s Law
Moseley’s Law




When the square root of the frequencies of the
characterstic x-rays from the elements is plotted
against the atomic number, a straight line is
obtained.
Moseley measured and plotted the x-ray frequencies
for about 40 of the elements of the periodic table.
He showed that the K-alpha x-rays followed a
straight line when the atomic number Z versus the
square root of frequency was plotted.
With the insights gained from the Bohr model, we
can write his empirical relationship as follows:
nK = ¾ cR (Z - 1)2
Significance of Moseley’s work



Moseley found a systematic shift towards shorter wavelengths as
one passed from one element to others of higher atomic weight,
but there were some irregularities. To get over the difficulty posed
by the irregularities, he assigned a number to each element,
specifying its position in the periodic table. Then he could assign a
relation between the frequency of X-ray lines and the atomic
number - a relation known as Moseley's law.
When the elements were arranged according to the atomic
numbers assigned by Moseley, some inconsistencies apparent in
the Mendeleev table were removed. Thus Moseley was the first to
arrange the elements in order of atomic number, rather than
atomic weight, so he can be considered to be responsible for the
present-day arrangement of the elements.
Moseley’s measurements also proved that the nucleus held an
integral number of elemental charges, thus placing the nuclear
model of the atom on a firm foundation.
X-ray Diffraction

If an incident X-ray beam encounters a crystal lattice,
general scattering occurs. Most scattering is
destructively interfered and is lost (destructive
interference).

Diffraction occurs when scattering in a certain
direction from one atomic plane is in phase with
scattered rays from other atomic planes. Under this
condition the reflections combine to form enhanced
wave fronts that mutually reinforce each other
(constructive interference). The relation by which
diffraction occurs is known as the Bragg law. Each
crystalline material has a characteristic atomic
structure and it will diffract X-rays in a unique
characteristic pattern.

Bragg’s Law:
2dsin = n
where  = X-ray wavelength,  = X-ray incident
angle, d = lattice spacing of atomic planes
(assuming a crystal)
The attenuation of x-rays
When x-rays go through matter, various
interactions will be happened in the
process. X-rays are absorbed by matter.
 x
Units of x, cm, , cm-1
0
Where I0 is the intensity of x-rays and I
is the intensity of x-rays after penetrating
through the x thickness of matter.
I I e
• The intensity decrease follows the
exponential rule.  is the linear attenuation
coefficient.

For a specific matter, the attenuation is
proportional to the density of the matter.
Because of this, the mass attenuation
coefficient, m,
m



•
It can be used to compare the absorbing
abilities among different materials.
•
If we introduce the mass thickness xm = 
x, the attenuation equation could be
written as
I  I 0e
  m xm
Units: xm (g·cm-2) , m (cm2 ·g-1)
Relation of attenuation coefficient
to the wavelength and atomic
number

For different atoms and different
wavelength of x-rays, the mass
attenuation coefficient is approximately
satisfied with the following relation:

 m  KZ 
K is generally a constant
 is about 3 ~ 4.
3