* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Document
Survey
Document related concepts
Transcript
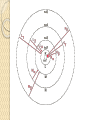
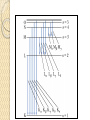
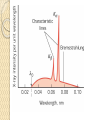
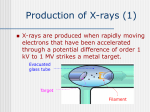
UNIT-IV X-RAYS X-RAYS • X-rays are electromagnetic waves • Their interaction with matter is governed by quantum theory. • The energy of x-ray photons is E = hv. • Wavelengths of x-rays is 0.001 to 10 nm Discovery of X-Rays Wilhelm Roentgen (1895) image from Cathode Ray Tube Site image from Wolfram Research High Energy Photons and Matter Production ◦ Bremsstrahlung Radiation (Continuum) ◦ Atomic and Nuclear Processes (Radioactive Decay) Fluorescence – Characteristic Lines (Inner Shell) Scatter – – – Photoelectric Effect (<50 keV) Compton Scattering (50 keV to 1 MeV) Pair Production (> 5 MeV) pair production from the wikipedia commons Production of X-rays X-rays are produced when rapidly moving electrons that have been accelerated through a potential difference of order 1 kV to 1 MV strikes a metal target. Production of X-rays Electrons from a hot element are accelerated onto a target anode. When the electrons are suddenly decelerated on impact, some of the kinetic energy is converted into EM energy, as X-rays. Less than 1 % of the energy supplied is converted into X-radiation during this process. The rest is converted into the internal energy of the target. Intensity of X-Rays To increase the intensity of x-rays, we need: to increase the tube current (more electrons) to increase tube voltage (increasing the energy of each x-ray photon). Under certain tube voltage, the current of filament control the intensity of x-rays. They are proportional to each other. The hardness of x-rays • The hardness of x-ray is defined as its penetrating ability. • It depends on the wavelength of the x-rays not on the number of x-ray photons. • The hardness of x-rays is proportional to the energy of x-ray photons. • Energy of x-ray photons is proportional to the voltage applied to the x-ray tube. Therefore, the hardness of x-rays is usually expressed by tube voltage in kV. Properties of X-rays X-rays travel in straight lines. X-rays cannot be deflected by electric field or magnetic field. X-rays have a high penetrating power. Photographic film is blackened by X-rays. Fluorescent materials glow when X-rays are directed at them. Photoelectric emission can be produced by X-rays. Ionization of a gas results when an X-ray beam is passed through it. Uses of X-rays In medicine To diagnose illness and for treatment. In industry To locate cracks in metals. X-ray crystallography To explore the structure of materials. X-RAY SPECTRA X-rays are emitted from the anode surface as a consequence of bombardment by the electron stream. Two distinct processes are involved in xray emission: (1) Some of the electrons are stopped by the target (2) Others transfer their energy in whole or in part to the atoms of the target to excite the atoms. The latter is the characteristic of the target, while the former emits continuous spectrum. X-ray Spectra X-ray Spectra The graph shows the following features ◦ A continuous background of X-radiation in which the intensity varies smoothly with wavelength. The background intensity reaches a maximum value as the wavelength increases, then the intensity falls at greater wavelengths. ◦ Minimum wavelength which depends on the tube voltage. The higher the voltage the smaller the value of the minimum wavelength. ◦ Sharp peaks of intensity occur at wavelengths unaffected by change of tube voltage. Continuous X-ray spectrum The x-rays from its tube usually contains different wavelengths and the plot of its intensity versus wavelength for spectrum of radiation emitted by an x-ray tube is called x-ray spectrum. Minimum wavelength in the X-ray Spectra When an electron hits the target its entire kinetic energy is converted into a photon. The work done on each electron when it is accelerated onto the anode is eV. Hence hf = eV and the maximum frequency f max eV h Therefore, min hc eV Characteristic X-ray Spectra Different target materials give different wavelengths for the peaks in the X-ray spectra. The peaks are due to electrons knock out innershell electrons from target atoms. When these inner-shell vacancies are refilled by free electrons, X-ray photons are emitted. The peaks for any target element define its characteristic X-ray spectrum. Characteristic X-Ray Spectra Bohr “shell” hypothesis. An electron shell based on the radius rn can be associated with each of the principle quantum numbers n. Electrons with lower values of n are more tightly bound to the nucleus than those with higher values. The radii of the orbits increase as n2 An energy is associated with each value of n Characteristic X-Ray Spectra When we add electrons to a fully ionized many-electron atom, the inner shells (low values of n) fill up before the outer shells. Historically n = 1 is K the shell, n = 2 is the L shell, n = 3 is the M shell, and so on. The Characteristic X-Ray Process Let a high-energy electron in an x-ray tube collides with an electron in the K shell (Electrons in the K shell are called K electrons.) in the target atom. If enough energy is transferred to the K electron to dislodge it from the atom, a vacancy is left in the K shell. The atom is stable in its lowest energy state, or ground state), so an electron from one of the higher shells will change its state and fill the inner shell vacancy at a lower energy. The Characteristic X-Ray Process A photon is emitted when the electron changes state. When this occurs in a heavy atom, the photon that is emitted is in the x-ray portion of the spectrum. E (x-ray) = Eu - El Moseley’s Law Moseley’s Law When the square root of the frequencies of the characterstic x-rays from the elements is plotted against the atomic number, a straight line is obtained. Moseley measured and plotted the x-ray frequencies for about 40 of the elements of the periodic table. He showed that the K-alpha x-rays followed a straight line when the atomic number Z versus the square root of frequency was plotted. With the insights gained from the Bohr model, we can write his empirical relationship as follows: nK = ¾ cR (Z - 1)2 Significance of Moseley’s work Moseley found a systematic shift towards shorter wavelengths as one passed from one element to others of higher atomic weight, but there were some irregularities. To get over the difficulty posed by the irregularities, he assigned a number to each element, specifying its position in the periodic table. Then he could assign a relation between the frequency of X-ray lines and the atomic number - a relation known as Moseley's law. When the elements were arranged according to the atomic numbers assigned by Moseley, some inconsistencies apparent in the Mendeleev table were removed. Thus Moseley was the first to arrange the elements in order of atomic number, rather than atomic weight, so he can be considered to be responsible for the present-day arrangement of the elements. Moseley’s measurements also proved that the nucleus held an integral number of elemental charges, thus placing the nuclear model of the atom on a firm foundation. X-ray Diffraction If an incident X-ray beam encounters a crystal lattice, general scattering occurs. Most scattering is destructively interfered and is lost (destructive interference). Diffraction occurs when scattering in a certain direction from one atomic plane is in phase with scattered rays from other atomic planes. Under this condition the reflections combine to form enhanced wave fronts that mutually reinforce each other (constructive interference). The relation by which diffraction occurs is known as the Bragg law. Each crystalline material has a characteristic atomic structure and it will diffract X-rays in a unique characteristic pattern. Bragg’s Law: 2dsin = n where = X-ray wavelength, = X-ray incident angle, d = lattice spacing of atomic planes (assuming a crystal) The attenuation of x-rays When x-rays go through matter, various interactions will be happened in the process. X-rays are absorbed by matter. x Units of x, cm, , cm-1 0 Where I0 is the intensity of x-rays and I is the intensity of x-rays after penetrating through the x thickness of matter. I I e • The intensity decrease follows the exponential rule. is the linear attenuation coefficient. For a specific matter, the attenuation is proportional to the density of the matter. Because of this, the mass attenuation coefficient, m, m • It can be used to compare the absorbing abilities among different materials. • If we introduce the mass thickness xm = x, the attenuation equation could be written as I I 0e m xm Units: xm (g·cm-2) , m (cm2 ·g-1) Relation of attenuation coefficient to the wavelength and atomic number For different atoms and different wavelength of x-rays, the mass attenuation coefficient is approximately satisfied with the following relation: m KZ K is generally a constant is about 3 ~ 4. 3