Download Lesson plan - Data Nuggets

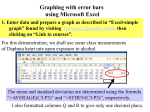
Stats workshop I
Learning objectives:
 explain when and why statistics are necessary
 identify the information gained from the mean, standard error (SE), and
standard error of the mean (SEM)
 understand the idea of random sampling, and that increasing sampling size
increases accuracy of your estimates
 understand confidence intervals are a measure of the accuracy of the mean
Start with brainstorming what statistics is on the whiteboard. Wikipedia: “Statistics
is the study of the collection, organization, analysis, and interpretation of data.” I
think that’s pretty good.
Example of human height (collect heights of all the students the night before – or
maybe on their pretest on arrival?). If we wanted to describe how tall people in this
class are, what could we do? (Hopefully they will hit on mean and a description of
the distribution – histogram, maybe even something like standard deviation). Put
up a slide with a histogram of their heights- you’re going to add an element at a time
to this figure as you go. Tell them you’re going to present three simple equations
that each build on the one before. First: the mean – add all the numbers together,
and divide by the number of observations.
This number gives us a measure of the middle of the distribution, but it doesn’t
describe the shape of the distribution very well (show examples of how you could
get the same mean with very different distributions). Ask what they might use to
describe this dimension of variation. Then introduce standard deviation. Breaking
it down: take the difference between the mean you just calculated and each value,
square it, add them all up, divide by (the number of observations – 1), take the
square root.
Up until now, we’ve been talking about the most basic, general statistics. But for the
next few days, we’ll be working with biological datasets. This means trying to
answer a question about a group of organisms where it’s not possible to measure
every single one. For example, what if instead of asking about height of people in
this room, we wanted to know about height of all junior and senior high school
students in Michigan. But we can’t afford to measure every single one of them. How
would you answer this question? (Guide a discussion about sampling – why is
random sampling important? Are the students in this room a good random
sample?) In the end, let’s make the assumption that this room IS a good random
sample. Now instead of KNOWING the mean of the population we’re interested in,
we’ve got an ESTIMATE of the mean. How do we decide how accurate that is? Using
the standard error of the mean (divide the standard deviation by the square root of
the number of observations):
So let’s talk a little more about the three statistics we’ve covered and sample size.
As you increase sample size, does it change the mean? (No) standard deviation?
(No) standard error of the mean? (Yes). Show how this happens in the equation.
Final point of the day: show the mean height as a bar graph with error bars. 2*SE =
95% confidence interval. So we have a single number that is our estimate of the
mean, but because it’s based on a SAMPLE, not measuring every member of the
population, we need an estimate of the accuracy of that mean. Using the SE, we can
put these bars on the graph to say, “we’re 95% confident that the real mean is in this
range.” This becomes really important if we try to answer a question comparing
two groups, for example, are juniors and seniors from Ohio shorter than those from
Michigan? (Show example bar graphs with same means and two different sets of
error bars.) We’ll talk more about this tomorrow.
For now, exploring these stats for ourselves with a new question: what’s proportion
of blue M&Ms in a package versus red M&Ms? (ANSWER: according to M&M
website, should be 24% blue, 13% red)
Split students into 10 groups (with 3 students per group). 5 groups are counting
red M&Ms, 5 groups are counting blue M&Ms. Each group gets 6 bags. Have every
group calculated the percent of blue or red M&Ms in each bag. Have them calculate
mean, standard deviation, and standard error for the number of blue or red M&Ms,
then graph their results as a bar graph (with an additional bar representing SE).
Have them plot the data from another group with a different color, looking to see if
the SEs overlap. Then enter all data into excel, plot all data, and compare red and
blue. Class excel sheet should show much smaller SEs than group plots, hopefully
with no overlap.