* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Chapter 15 - SFA Physics and Astronomy
Traditional sub-Saharan African harmony wikipedia , lookup
Circle of fifths wikipedia , lookup
Strähle construction wikipedia , lookup
Consonance and dissonance wikipedia , lookup
Mode (music) wikipedia , lookup
Interval (music) wikipedia , lookup
Microtonal music wikipedia , lookup
Equal temperament wikipedia , lookup
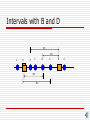
Chapter 15 Successive Tones: Reverberations, Melodic Relationships, and Musical Scales Audibility of Decaying Sounds in a Room The first of the tone we hear is the directly propagated wave. Because of the precedence effect, the direct wave will combine with the most direct reflections (within 30 to 50 milliseconds) and be perceived as one. Picture of a Clearly Heard Tone Decay – similar to the attack Attack – heard as one because of Precedence Effect Reverberation Time The time required for the sound to decay to 1/1000th of the initial SPL Audibility Time Use a stopwatch to measure how long the sound is audible after the source is cut off Agrees well with reverberation time It is constant, independent of frequency, and unaffected by background noise Why does Audibility Time Work? Threshold of hearing temporarily shifted to 60 dB below a loud tone? 60 dB is 1000 times in SPL which then matches the definition of Reverberation Time Measurements show that this happens, but only for a few tenths of a second Not long enough to make audibility time work Why does Audibility Time Work? The ear is responding to the rate of change of loudness? Look at example on next slide Advantages of Audibility Time Only simple equipment required Many sound level meters can only measure a decay of 40-50 dB, not the 60 dB required by the definition Instruments assume uniform decay of the sound, which may not be the case Device to Study Successive Tones Tone Generator 1 1 2 Tone Generator 2 Switch Amplifier Speaker Notes on Tone Switcher Tone generators produce fundamental plus a few harmonics to simulate real instruments Switching cannot be heard Reverberation time at least ⅓ sec. Experiment Start with TG1 on C4 Switch to TG2 and adjust At certain frequencies the decaying TG1 will form beats with the partials or heterodyne components of TG2 The beats will be most audible when the amplitudes are equal. Using Reverberation These experiments show that we can use reverberation as an aid in performing It is easier to perform in a live room (shower) Noise can mask the decaying partials and make pitch recognition more difficult Conclusions We can set intervals easily for successive tones (even in dead rooms) so long as the tones are sounded close in time. Setting intervals for pure sinusoids (no partials) is difficult if the loudness is small enough to avoid exciting room modes. At high loudness levels there are enough harmonics generated in the room and ear to permit good interval setting. Intervals set at low loudness with large gaps between the tones tend to be too wide in frequency. The Beat-Free Chromatic (or Just) Scale We will use the Tone Switcher to help find intervals that produce beat-free relationships to the fundamental. The fact that the frequency generators contain harmonics makes this possible Notice that the octave is a doubling of the frequency and the next octave would be four times the frequency of the fundamental First Important Relationship Three times the fundamental less an octave 3f/2 or an interval of 3/2 or a fifth Fundamental will have harmonics that contain the fifth Five such relationships can be found in the first octave Just Intervals (with respect to C4) Chromatic Scales Listed Interval Interval Computed Cent Frequency Name Ratio Frequency Difference (equal-tempered) (beat-free) C 261.63 E 329.63 3rd 5/4 327.04 14 F 349.23 4th 4/3 348.84 2 G 392.00 5th 3/2 392.45 -2 A 440.00 Major 6th 5/3 436.05 16 C 523.25 octave 2/1 523.26 0 Relationships Among Five Principles Note Frequency (equal-tempered) Interval Ratio Interval Name Resulting Frequency Note F 349.23 3/2 5th 523.85 C E 329.63 4/3 4th 439.51 A G 392.00 4/3 4th 522.67 C F 349.23 5/4 3rd 436.54 A E 329.63 6/5 Minor 3rd 395.52 G A 440.00 6/5 Minor 3rd 528.00 C Finding the Missing Steps Notice the B and D are not harmonically related to C Finding B A fifth (3/2) above E gives 490.56 Hz A third (5/4) above G gives 490.00 Hz Difference is 2 cents – sensibly equal The Trouble with D A Fourth (4/3) below G gives 294.34 Hz A Fifth (3/2) below A gives 290.70 Hz Difference is 22 cents or 1¼% Sounded together these “D’s” give clear beats Intervals with B and D 5th 3rd C D E F G 4th 5th A B C Filling in the Scale 3rd C E D F 3rd G A B C 4th 3rd 3rd Minor 6 Notice that C#, Eb, and Bb come into the scheme, but Ab/G# is another problem. Putting numbers to the Ab/G# Problem From at Interval Ratio Giving E 327.04 Third 5/4 408.80 C 523.26 Third 5/4 418.61 The Problem with F# C D E F 3rd G A B min3 3rd Other discrepancies exist but these highlight the problem. C Saving the Day As the speed increases discrepancies in pitch are more difficult to detect. The sound level is greater at the player’s ear than the audience. He can make small adjustments. He is always better tuned than the audience demands. Working Toward Equal Temperament The chromatic (Just) scale uses intervals which are whole number ratios of the frequency. Scales have unequal intervals E 327.04 F 348.84 1.0666 16/15 B 490.5 1.0667 16/15 C 523.26 but C# 279.07 D1 290.7 1.0417 F 348.84 F#1 363.38 1.0417 Making the Interval Equal An octave represents a doubling of the frequency and we recognize 12 intervals in the octave. Make the interval 12 2 1.059463 Using equal intervals makes the cents division more meaningful The following table uses Breaking Up One Interval Interval in Cents Frequency Ratio Frequency Note 0 1.00000 261.63 C4 10 1.00579 263.15 20 1.01162 264.67 30 1.01748 266.20 40 1.02337 267.75 50 1.02930 269.30 60 1.03526 270.86 70 1.04126 272.43 80 1.04729 274.00 90 1.05336 275.59 100 1.05946 277.19 D4 Comparison Frequency Ratio Musical Interval Cents (Just) Cents (EqualTempered) 1/1 Unison 000 000 2/1 Octave 1200 1200 3/2 Fifth 702 700 4/3 Fourth 498 500 5/3 Major sixth 884 900 5/4 Major third 386 400 6/5 Minor third 316 300 8/5 Minor sixth 814 800 Pitch Discrepancy Groups When pitch discrepancies exist in a scale, the cent difference from the equal-tempered interval cluster into three groups Low Group Middle Group High Group 12 cents low Equal-tempered frequency 12 cents high Each group has a range of about 7 cents If a player is asked to sharp/flat a tone, (s)he invariably goes up/down about 10 cents, moving from one group to another. Complete Scale Comparison Interval Ratio to Tonic Just Scale Ratio to Tonic Equal Temperament Unison 1.0000 1.0000 Minor Second 25/24 = 1.0417 1.05946 Major Second 9/8 = 1.1250 1.12246 Minor Third 6/5 = 1.2000 1.18921 Major Third 5/4 = 1.2500 1.25992 Fourth 4/3 = 1.3333 1.33483 Diminished Fifth 45/32 = 1.4063 1.41421 Fifth 3/2 = 1.5000 1.49831 Minor Sixth 8/5 = 1.6000 1.58740 Major Sixth 5/3 = 1.6667 1.68179 Minor Seventh 9/5 = 1.8000 1.78180 Major Seventh 15/8 = 1.8750 1.88775 Octave 2.0000 2.0000 Indian Music Comparisons Indian music uses a generalize seven note scale like the do re mi of Western music. Indian sa re ga ma pa dha ni sa Western do re mi fa sol la ti do Letter C D E F G A B C The Reference Raga The rag is the most important concept of Indian music. The Hindi/Urdu word "rag" is derived from the Sanskrit "raga" which means "color, or passion". It is linked to the Sanskrit word "ranj" which means "to color". The Alap An Indian piece will usually open with an alap, notes going up and down the scale to establish position and relationship. They will play around a tone, the tone evasion becoming very elaborate. It becomes a game between the player and the listeners. Jazz has similar variations. Indian Modes Play Bilawal Play Kafi Pitch Variations In Western music we have similar pitch wanderings (vibrato, for example) that the Indian musician would find strange. We almost always make abrupt transitions from one note to the next without the slides of Indian music.