* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Distribution of the Sample Means
Survey
Document related concepts
Transcript
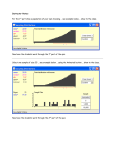
Distribution of the Sample Means Topics: • • • • • Essentials Distributions Sampling Error Distribution of the Sample Means Properties of the Distribution: • 1) Mean • 2) Std. Dev. • 3) Central Limit Theorem A large sample in statistics Example: Calculating and Additional Topic x x • • • x x Essentials: Distribution of Sample Means (A distribution unlike others) Be able to explain what the Distribution of Sample Means represents. Know the three characteristics of this distribution. Be able to use a set of data demonstrate the calculation of the mean and standard deviation of this distribution. What is a statistically large sample? Some Common Distribution Shapes Distribution of the Sample Means Sampling Error: – the difference between the sample measure and the population measure due to the fact that a sample is not a perfect representation of the population. – the error resulting from using a sample to estimate a population characteristic. Distribution of the Sample Means Distribution of the Sample Means – is a distribution obtained by using the means computed from random samples of a specific size taken from a population. Distribution of the Sample Mean, x – the distribution of all possible sample means for a variable x, and for a given sample size. Properties of the Distribution of Sample Means 1. 2. The mean of the sample means will be the same as the population mean. The standard deviation of the sample means will be smaller than the standard deviation of the population, and it will be equal to the population standard deviation divided by the square root of the sample size. A Third Property of the Distribution of Sample Means A third property of the distribution of the sample means concerns the shape of the distribution, and is explained by the Central Limit Theorem. The Central Limit Theorem As the sample size n increases, the shape of the distribution of the sample means taken from a population with mean and standard deviation will approach a normal distribution. This distribution will have mean and standard deviation n Two Important Things to Remember When Using The Central Limit Theorem 1. 2. When the original variable is normally distributed, the distribution of the sample means will be normally distributed, for any sample size n. When the distribution of the original variable departs from normality, a sample size of 30 or more is needed to use the normal distribution to approximate the distribution of the sample means. The larger the sample, the better the approximation will be. An Example Suppose I give an 8-point quiz to a small class of four students. The results of the quiz were 2, 6, 4, and 8. We will assume that the four students constitute the population. The Mean and Standard Deviation of the Population (the four scores) The mean of the population is: 2648 5 4 The standard deviation of the population is: (2 5)2 (6 5)2 (4 5)2 (8 5)2 2.236 4 Distribution of Quiz Scores Frequency 1.0 0.5 0.0 2 4 6 Score 8 All Possible Samples of Size 2 Taken With Replacement SAMPLE MEAN 2,2 2,4 2,6 2,8 4,2 4,4 4,6 4,8 2 3 4 5 3 4 5 6 SAMPLE 6,2 6,4 6,6 6,8 8,2 8,4 8,6 8,8 MEAN 4 5 6 7 5 6 7 8 Frequency Distribution of the Sample Means MEAN 2 3 4 5 6 7 8 f 1 2 3 4 3 2 1 Distribution of the Sample Means 4 Frequency 3 2 1 0 2 3 4 5 6 Sample Mean 7 8 The Mean of the Sample Means Denoted x In our example: 23 453 45 6 45 6 7 5 6 7 8 x 5 16 So, x , which in this case = 5 The Standard Deviation of the Sample Means Denoted x In our example: (2 5)2 (3 5)2 (4 5)2 (5 5)2 ... (8 5)2 x 1.581 16 Which is the same as the population standard deviation divided by 2 2.236 1.581 2 Additional Topic: Demonstration showing increasing sample size yielding better estimations of the population value. Heights of Five Starting Players on a Men’s Basketball Team (inches) Possible Samples of Size n = 2 From a Population of Size N = 5 Possible Samples of Size n = 4 From a Population of Size N = 5 Dot plots of the Sampling Distributions for Various Sample Sizes (N = 5)
























![z[i]=mean(sample(c(0:9),10,replace=T))](http://s1.studyres.com/store/data/008530004_1-3344053a8298b21c308045f6d361efc1-150x150.png)