Download Rotational spectroscopy

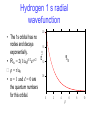
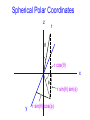
Spectroscopy
Lecture 3
Hydrogen Atom
Rotational Spectroscopy
NC State University
Experimental observation of
hydrogen atom
• Hydrogen atom emission is “quantized”. It
occurs at discrete wavelengths (and therefore
at discrete energies).
• The Balmer series results from four visible
lines at 410 nm, 434 nm, 496 nm and 656 nm.
• The relationship between these lines was
shown to follow the Rydberg relation.
The Solar Spectrum
• There are gaps in the solar emission
called Frauenhofer lines.
• The gaps arise from specific atoms in
the sun that absorb radiation.
Atomic spectra
• Atomic spectra consist of series of narrow lines.
• Empirically it has been shown that the
wavenumber of the spectral lines can be fit by
where R is the Rydberg constant, and n1 and n2 are
integers. Note that n2 > n1.
Schrödinger equation for hydrogen:
The kinetic energy operator
The Schrö dinger equation in three dimensions is:
2
2
h
–
  + V = E
2
The operator del-squared is:
2
2
2



 = 2+ 2+ 2
x
y
z
2
The procedure uses a spherical polar coordinate system.
Instead of x, y and z the coordiantes are q, f and r.
The Bohr radius
The quantity a0 = 4pe0h2/me2 is known as the Bohr
radius. The Bohr radius is a0 = 0.529 Å . Since it
emerges from the calculation of the wave functions and
energies of the hydrogen atom it is a fundamental unit.
In so-called atomic units the unit of length is the Bohr
radius. So 1 Å is approximately 2 Bohr radii.
You should do a dimensional (unit) analysis and verify
that a0 has units of length!
Energy levels of hydrogen atom
• The energy levels of the hydrogen atom are
specified by the principal quantum number n:
• All states with the same quantum number n
have the same energy.
• All states of negative energy are bound states,
states of positive energy are unbound and are
part of the continuum.
The Rydberg Constant
• The energy levels calculated using the
Schrö dinger equation permit calculation of the
Rydberg constant.
• One major issue is units. Spectroscopists often
use units of wavenumber or cm-1. At first this
~
seems odd, but hn = hc/l = hcn where n is ~the
value of the transition in wavenumbers.
in cm-1
The simple form
• Using the Rydberg constant the energy of the
hydrogen atom can be written as:
~
R
E= – 2
n
~
where R = 109,636 cm-1
Shells and subshells
• All of the orbitals of a given value of n for a shell.
• n = 1, 2, 3, 4 .. correspond to shells K, L, M, N…
• Orbitals with the same value of n and different
values of l form subshells.
• l = 0, 1, 2, ... correspond to subshells s, p, d …
• Using the quantum numbers that emerge from
solution of the Schrö dinger equation the
subshells can be described as orbitals.
Spherical harmonics
These are the spherical harmonics
, which
are solutions of the angular Schrodinger equation.
Hydrogen 1 s radial
wavefunction
• n = 1 and l = 0 are
the quantum numbers
for this orbital.
1.5
R1,0
• The 1s orbital has no
nodes and decays
exponentially.
• R1s = 2(1/a0)3/2e-r/2
 r = r/a0
2.0
Y1s
1.0
0.5
0
2
4
r
6
8
10
The Radial Distribution in
Hydrogen 2s and 2p orbitals
Rn,
0.6
Y2s
Y2p
0.4
0.2
0.0
0
2
4
r
6
8
10
The Dipole Moment Expansion
The permanent dipole moment of a molecule
oscillates about an equilibrium value as the
molecule vibrates. Thus, the dipole moment
depends on the nuclear coordinate Q.

 Q = 0 +
Q + ...
Q
where  is the dipole operator.
Rotational Transitions
Rotational transitions arise from the rotation
of the permanent dipole moment that can
interact with an electromagnetic field in the
microwave region of the spectrum.

 Q = 0 +
Q + ...
Q
Spherical Polar Coordinates
z
r
q
r cos(q)
x
f
r sin(q) sin(f)
y
r sin(q) cos(f)
Rotation in two dimensions
Our first approach is classical.
The angular momentum is Jz = pr.
Jz
r
m
p
Using the deBroglie relation p = h/l we also
have a condition for quantization of angular
motion Jz = hr/l.
Classical Rotation
In a circular trajectory Jz = pr and E = Jz2/2I.
I is the moment of inertia.
Diatomic I = r2
Mass in a circle I = mr2.
r
m
r
m1
m2
m 1m 2
Reduced mass  = m + m
1
2
The 2-D rotational hamiltonian
• The wavelength must be a whole number
fraction of the circumference for the ends to
match after each circuit.
• The condition 2pr = Ml combined with the
deBroglie relation leads to a quantized
expression,Jz = Mh where M is a quantum
number for rotation in two dimensions.
• The hamiltonian is:
Energy level spacing
Energy levels
Energy Differences
of DJ = ± 1
Quantization of rotational motion:
solution of the f equation
The corresponding wavefunctions are:
with the constraint that:
Since the energy is constrained to values Jz2/2I we
find that
The wavefunctions of a rigid rotor are
called spherical harmonics
The solutions to the q and f equation (angular part)
are the spherical harmonics Y(q,f )= Q(q)F(f)
Separation of variables using the functions Q(q)
and F(f) allows solution of the rotational wave
equation.
2
h

Y
1
1  sinq Y
–
+
q
2I sin2q  2 sinq q
2
= EY
We can obtain a q and f equation from the above
equation.
Rotational Wavefunctions
J=0
J=1
J=2
These are the spherical harmonics YJM, which
are solutions of the angular Schrodinger equation.
The form of the spherical harmonics
Including normalization the spherical harmonics are
Y00 = 1
4p
0
3 cosq
Y1 = 4p
±1
Y1
=
Y20 =
±1
2
Y =
3 sinqe ±if 2
Y2 =
8p
5 3cos2q – 1
16p
15 sinqcosqe ±if
8p
15 sin2qe ±2if
32p
The form commonly used to represent p and d
orbitals are linear combinations of these functions
Euler relation
Linear combinations are formed using the Euler relation
e
±if
= cosq ±isinq
if
–if
e
–
e
sinq 
2i
if
–if
cosq  e + e
2
Projection along the z-axis is usually taken using
z = rcosq. Projection in the x,y plane is taken using
x = rsinqcosf and y = rsinqsinf
Solutions to the 3-D rotational
hamiltonian
• There are two quantum numbers
J is the total angular momentum quantum number
M is the z-component of the angular momentum
• The spherical harmonics called YJM are functions whose
probability |YJM|2 has the well known shape of the s, p and
d orbitals etc.
J = 0 is s , M = 0
J = 1 is p , M = -1, 0 , 1
J = 2 is d , M = -2 , -1, 0 , 1, 2
J = 3 is f , M = -3 , -2 , -1, 0 , 1, 2, 3
etc.
The degeneracy of the solutions
• The solutions form a set of 2J + 1 functions at each
energy (the energies are
• A set of levels that are equal in energy is called a
degenerate set.
J=3
J=2
J=1
J=0
Orthogonality of wavefunctions
• The rotational wavefunctions can be represented as the
product of sines and cosines.
• Ignoring normalization we have:
• s 1
• p cosq, sinqcosf, sinqsinf
• d 1/2(3cos2q - 1), cos2qcos2f , cos2qsin2f ,
cosqsinqcosf , cosqsinqsinf
• The differential angular element is sinqdqdf/4p over
• the limits q = 0 to p and f = 0 to 2p.
• The angular wavefunctions are orthogonal.
Orthogonality of wavefunctions
• For the theta (q) integrals we can use the substitution
• x = cosq and dx = sinqdq
• For example, for s and p-type rotational wave functions,
for the theta integral we have
• Using these substitutions we can turn all of these integrals
into polynomials.
The moment of inertia
The kinetic energy of a rotating body is 1/2Iw2.
The moment of inertia is given by:

I=
 mr
i=1
2
i i
The rigid rotor approximation assumes that
molecules do not distort under rotation. The types
or rotor are (with moments Ia , Ib , Ic)
- Spherical: Three equal moments (CH4, SF6)
(Note: No dipole moment)
- Symmetric: Two equal moments (NH3, CH3CN)
- Linear: One moment (CO2, HCl, HCN)
(Note: Dipole moment depends on asymmetry)
- Asymmetric: Three unequal moments (H2O)
Polyatomic Molecules
• There are 3N total degrees of freedom in a
molecule that contains N atoms.
• There are three translational degrees of freedom.
These correspond to motion of the center of mass
of the molecule.
• In a linear molecule there are two rotational
degrees of freedom. In a non-linear molecule there
are 3 rotational degrees of freedom.
• The remaining degrees of freedom are vibrational.
Spectroscopy of atomic hydrogen
• Spectra reported in wavenumbers (cm-1)
• Rydberg fit all of the series of hydrogen spectra
with a single equation,
n=R 1 – 1
n
n
• Absorption or emission of a photon of frequency
n occurs in resonance with an energy change,
DE = hn (Bohr frequency condition).
• Solutions of Schrö dinger equation result in
further selection rules.
2
1
2
2
Spectroscopic transitions
• A transition requires a transfer from one state
with its quantum numbers (n1, l1, m1) to another
state (n2, l2, m2).
• Not all transitions are possible: there are
selection rules, Dl =  1, m = 0,  1
• These rules demand conservation of angular
momentum. Since a photon carries an intrinsic
angular momentum of 1.
The interaction of electromagnetic
radiation with a transition moment
The electromagnetic wave has an angular
momentum of 1. Therefore, an atom or
molecule must have a change of 1 in its
orbital angular momentum to conserve this
quantity. This can be seen for hydrogen atom:
Electric vector
of radiation
l=0
l=1
A propagating wave of electromagnetic radiation
of wavelength l has an oscillating electric dipole, E
(magnetic dipole not shown)
l
E
The oscillating electric dipole, E, can induce an oscillating dipole
in a molecule as the radiation
passes through the sample
l
E
The oscillating electric dipole, E, can induce an oscillating dipole
in a molecule as the radiation passes through the sample
l
n=1
∆E = hc/l
n=0
The type of induced oscillating dipole depends on l.
If l corresponds to an electronic energy gap, then radiation will be
absorbed, and a molecular electronic transition will result
The oscillating electric dipole, E, can induce an oscillating dipole
in a molecule as the radiation passes through the sample
l
LUMO
∆E = hc/l
HOMO
If l corresponds to a electronic energy gap, then radiation will be
absorbed, and an electron will be promoted to an unfilled MO
The oscillating electric dipole, E, can induce an oscillating dipole
in a molecule as the radiation passes through the sample
l
R
v=1
O
R
∆E = hc/l
R
v=0
O
R
The type of induced oscillating dipole depends on l.
If l corresponds to a vibrational energy gap, then radiation will
be absorbed, and a molecular vibrational transition will result
Rotational spectroscopy
Rotational Transitions
• Electromagnetic radiation can interact with a molecule to
change the rotational state.
• Typical rotational transitions occur in the microwave
region of the electromagnetic spectrum.
• There is a selection rule that states that the quantum
number can change only by + or - 1 for an allowed
rotational transition (DJ = 1).
J=2
J=1
J=0
Rotational Transitions
• Treat the electromagnetic wave as having a polarization
along x, y, or z.
• The transition integral is not zero in this case since the zpolarized transition is matched to the pz rotational orbital.
The total wave function in
calculation of transition moment
The total wave function can be factored into
an electronic, a vibrational and a rotational
wave function.
 =  el vYJM
M rot =
=
=
 *vYJM
 *el  eld el  vYJMd nuc
 *vYJM 0 vYJMd nuc
 *v vdQ YJM 0YJMsinqdqdf
The rotational transition moment
The transition moment is a dipolar term that
connects two states. Here we are considering
rotational states that have quantum numbers
J, M in the initial state and J’,M’ in the final
State
Mrot = 0 YJMYJMsinqdqdf
The electronic integral gives 0, the permanent
dipole moment. The vibrational wave functions
are normalized and the integral is 1.
Interaction with radiation
For example, if an oscillating electromagnetic
field enters as E0cos(wt)cos(q) such that
hw is equal to a rotational energy level
difference, the interaction of the electric field
with the transition moment is
2p
MrotM=rotE=0  0
p
cos q YJMsin q dqdf
*
J+1,M
Y
0
0
Interaction with radiation
The choice of cos(q) means that we consider
z-polarized microwave light. In general
we could consider x- or y-polarized as well.
x sin(q)cos(f)
 0 =  X i +  Y j +  Zk
y sin(q)sin(f)
 0 =  0 sinqcosfi + sinqsinf j +cosqk
z cos(q)
Pure rotational spectra
• A pure rotational spectrum is obtained by
microwave absorption.
• The range in wavenumbers is from 0-200 cm-1.
• Rotational selection rules dictate that the
change in quantum number must be
DJ = ± 1
• A molecule must possess a ground state dipole
moment in order to have a pure rotational
spectrum.
Energy level spacing
Energy levels
Energy Differences
of DJ = ± 1
The rotational constant
The spacing of rotational levels in spectra is given
by DE = EJ+1- EJ according to the selection rule
The line spacing is proportional to the rotational
constant B
In units of wavenumbers (cm-1) this is:
A pure rotational spectrum
~
2B
A pure rotational spectrum is observed in the
microwave range of electromagnetic spectrum.
Key Points
• The vibrational energy levels are given by:
The energy levels have a degeneracy of 2J + 1
• The wave functions are the spherical harmonics.
Transition energies are given by:
• B is the rotational constant
• Rotational spectra consist of a series lines
separated by 2B.