* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Describing a sample
Survey
Document related concepts
Transcript
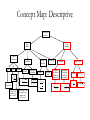
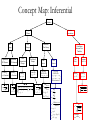
EDUC 200C week10 December 7, 2012 Two main ideas… • Describing a sample – Individual variables (mean and spread of data) – Relationships between two variables (correlation) • Making inferences about the population from the sample – One sample (t-test) – Two samples (t-test) – Two or more samples (ANOVA) DESCRIBING A SAMPLE Describing a sample • Individual variables – Central tendency • Mean, median, mode – Variability • Spread of observations around the mean • Variance • Standard deviation Describing a sample • Relative position – z scores – Data transformation to give data a mean on 0 and a standard deviation of 1 Describing a sample • The relationship between two ore more variables – Measure of the strength of relationship – Pearson correlation (between two continuous variables) • Z-score difference formula • Z-score product formula • Raw score formula – Spearman rank-order correlation coefficient (two rank order variables) Describing a sample • Regression – Predict Y from X: – – – Error (or residual): – Standard error: – r-squared: INFERENCE The Normal Distribution Inference • Type I and Type II error H0 True H0 False Reject H0 Type I error α Correct! Power: 1-β Retain H0 Correct! Confidence: 1-α Type II error β Inference • Power reflects our ability to correctly reject the null hypothesis when it is false • Must have a specific alternative hypothesis in mind – Alternatively, we can specify a target power level and, with a particular sample size determine how big of an effect we will be able to detect • We have higher power with larger samples and when testing for large effect sizes • There is a tradeoff between α and power Inference • One Sample – H0: μ=some number – Population standard deviation (σ) known • Standard error: • • Compare to normal distribution • Confidence interval: – Population standard deviation not known • Standard error: • • Compare to t distribution • Confidence interval: Inference • Two samples – Independent samples • H0: μ1= μ2 • Pooled variance: • Standard error: • • Confidence interval: Inference • Matched pairs – – H0: μD=0 – Standard error: – – Compare to t distribution Inference • More than two samples – – Compare to F distribution – One-way ANOVA • H0: μ1= μ2 =…= μk – Two-way ANOVA (factorial design) • H0: μa1= μa2 =…= μaj μb1= μb2 =…= μbl μaxb1= μaxb2 =…= μaxbk – Degrees of freedom will vary with number of groups and levels within factors Concept Map: Descriptive Descriptive Statistics One Variable Central Tendency Mode X X N The most frequent Xi The value of the middle case (if N is odd) Relative Standing Variability Median Mean Two Variables s2 Variance (X X ) Standard Deviation 2 N 1 The average of the values of the two middle cases (if N is even) s (X X ) N 1 Percentile Rank Z score 2 z X X X z s Frequency Correlation Pearson Correlation Coefficient (interval/ratio) or r Z X ZY N 1 Regression Spearman Correlation Coefficient (Ordinal) rs 1 6 D2 N ( N 2 1) Slope Intercept sY sX a Y bX br Concept Map: Inferential Inferential Statistics Compare Means One Group Two Groups Population SD Known Population SD Unknown Two Independent Groups z-test H0: µ = Constant t-test H0: µ = Constant t-test H0: µ1 = µ 2 z X / N t Examine Associations X s/ N df N 1 t More than Two Group Two Paired Groups One-way ANOVA H0: µ1 = µ 2 = µ p = µ t-test H0: µD = 0 X1 X 2 ( N1 1) s12 ( N 2 1) s22 1 1 * N1 N 2 2 N1 N 2 df N1 N 2 2 One Factor t D sD / N df N 1 F MS Between MSW ithin df B g 1 dfW N g Correlation between Two Variables Two Factors Two-way ANOVA H0: A: µ1 = µ2 = …= µq B: µ1 = µ2 = …= µr AB: Interaction = 0 Test One r Compare Two r’s t-test H0: ρ=0 z-test H0: ρ1 = ρ2 zobs FA MS A MSW FB MS B MSW FAB MS AB Interaction MSW ithin df A p 1 df B q 1 df AB ( p 1)( q 1) dfW N pq t obs robs 2 1 robs N 2 Or compare rcritical with robs z r1 z r2 1 1 N1 3 N 2 3 Final Exam will be posted tomorrow on Coursework…due December 14. (I’ll send out an email to let you know it’s there.) Thanks for a great quarter!!