Download Chapter 13: universal gravitation

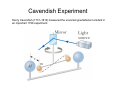
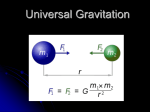
Chapter 13: universal gravitation
Newton’s law of universal gravitation
Newton’s law of universal gravitation: every particle in the Universe attracts
every other particle with a force that is directly proportional to the product of
their masses and inversely proportional to the square of the distance between
them.
where G ≈ 6.674×10-11 N m2 kg-2.
Note that the masses are assumed to be point masses with no significant size
relative to the distance the two points. The force of gravity is always an
attractive force, where the gravitational force vectors of two particles are always
pointed towards each other.
For a spherically symmetric mass distribution, the force on a particle outside the
distribution is the same as that for a point charge.
Cavendish Experiment
Henry Cavendish (1731–1810) measured the universal gravitational constant in
an important 1798 experiment.
Gravitational acceleration near the
Earth’s surface
The gravitational acceleration at the surface of the Earth is
where
and
The gravitational acceleration at some height h is then
.
Gravitational acceleration near the
Earth’s surface (cont.)
For h < RE we can do a geometric expansion of the denominator about h/RE,
which gives
When h << RE, then
Work due to universal gravitation
From earlier we learned the relationship between the work due to a force and
the distance
If we are concerned with being outside a spherical mass, and we are interested
in great distances such that the force is not approximated as a constant, and
displacements along the radial direction,
Work due to universal gravitation (cont.)
We know that the work due to gravity is related to the potential energy,
. Setting
, we find
In general for a small object and a mass of any distribution, the gravitational
potential energy from Newton’s universal law of gravity is given by
where
is the mass of the small test object.
Example with potential energy
Potential energy of a point mass along the principal axis of the center of a ring of
uniform mass density and radius R
Example #2 with potential energy
Potential of a point mass in a semicircle of uniform mass density
Satellites in orbit
- Remember that centripetal acceleration is
- The magnitude of the force is
which gives
- Newtons law of gravity is
- Determine the sum of the forces,
- The only acceleration is
, so
A
- We know the circumference of a circle and that
velocity, therefore
is a constant
B
- Find the radius of orbit by plugging in B into A and solving for
radius of the orbit,
.
gives the
Work and circular orbits
How much work is done on a
satellite to have it orbit 1 period?
NO WORK DONE!!!
and therefore
Thus,
Kepler's laws of planetary motion
Kepler's first law: planets are orbiting the sun in a path described as an ellipse,
where the sun is at one focus of the ellipse.
Kepler's second law: The radius vector sweeps equal areas in equal times for
a planet in motion around the sun.
Kepler's third law: The period of a planet's orbit squared is proportional to its
average distance from the sun cubed.
The circular orbit solution for the period can be extended to an elliptical orbit by
replacing the “r” by the semi-major axis “a”
Gauss's law for the gravitational field
Gauss's law for gravitation in integral form is
The left-hand-side of the equation is the flux,
flux through an arbitrary surface is defined as
, through a closed surface. The
In differential form, Gauss’s law for gravitation becomes