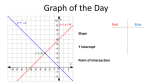
* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download 3/28 Intro. to Trig. notes File
Metric tensor wikipedia , lookup
Riemannian connection on a surface wikipedia , lookup
Perceived visual angle wikipedia , lookup
List of works designed with the golden ratio wikipedia , lookup
Euclidean geometry wikipedia , lookup
Golden ratio wikipedia , lookup
Rational trigonometry wikipedia , lookup
Integer triangle wikipedia , lookup
Pythagorean theorem wikipedia , lookup
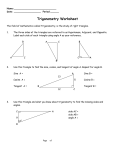
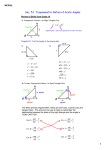
Introduction to Trigonometry Unit IIC Day 3 Do Now Geometry Review: The Angle-Angle Similarity Theorem states that if two triangles have two pairs of congruent angles, then the triangles are similar. Are the following triangles similar? If so, how would you prove it? Trigonometry Trigonometry is the study of ratios of sides in right triangles. We refer to sides in relation to a given angle as opposite the angle, adjacent to the angle, or as the hypotenuse. Ex. 1: Identifying Side Lengths a) If you are “standing” at vertex D, which side is the hypotenuse? Which is the opposite side? Which is the adjacent side? b) If you are “standing” at vertex E, which side is the hypotenuse? Which is the opposite side? Which is the adjacent side? Note on Sides We never “stand” at the right angle. The hypotenuse is the hypotenuse; it is never considered adjacent even though it might appear to be. Ex. 2: Ratios “Standing” at vertex G, what is the ratio of the opposite side to the adjacent side? What does this ratio represent? Ex. 2A: Ratios “Standing” at vertex B, what is the ratio of the opposite side to the adjacent side? What does this ratio represent? Ex. 3: Comparing Ratios a) Standing at angle A, what is the ratio of the opposite side to the adjacent side? b) Standing at angle D, what is the ratio of the opposite side to the adjacent side? c) Standing at angle G, what is the ratio of the opposite side to the adjacent side? What can we conclude about the ratio of the opposite to the adjacent anytime we are standing at the 45 angle of any right triangle? The Tangent Function The tangent of an angle in a right triangle is the ratio of the opposite side length to the adjacent side length. We can think of tangent as a function that takes an angle measure as its input and gives the ratio opposite/adjacent as its output. Angle (º) Opp./Adj. 15º 30º 45º 60º Ex. 4: Finding Tangent a) Find the tangent of R. a) Find the tangent of S. Six Trigonometric Ratios There are six trig. ratios: sine, cosine, tangent cosecant, secant, and cotangent Ex. 5 Find the six trigonometric ratios for R in the triangle above.