* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download File - Ms. Brown`s class
Steinitz's theorem wikipedia , lookup
Golden ratio wikipedia , lookup
Technical drawing wikipedia , lookup
Approximations of π wikipedia , lookup
Tessellation wikipedia , lookup
Regular polytope wikipedia , lookup
Perceived visual angle wikipedia , lookup
Multilateration wikipedia , lookup
Shapley–Folkman lemma wikipedia , lookup
Rational trigonometry wikipedia , lookup
Euler angles wikipedia , lookup
Complex polytope wikipedia , lookup
List of regular polytopes and compounds wikipedia , lookup
Trigonometric functions wikipedia , lookup
History of trigonometry wikipedia , lookup
Pythagorean theorem wikipedia , lookup
Euclidean geometry wikipedia , lookup
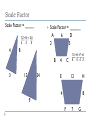
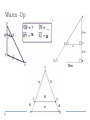
Warm Up Solve each proportion. 1. 3 = 15 x 20 3. x 35 2. 3 4 24 y 4 7 5 ACTIVITY 30min ` Materials Need glue & scissors Dissections of Squares Critical Thinking Cut out each figure (one at a time) and rearrange pieces to form a square. Glue pieces in the square provided. Polygons and Similarities 6.1 and Chapter 7 6.1 Properties and Attributes of Polygons To identify and name polygons To find the sum of the measures of interior and exterior angles of convex polygons and measures of interior and exterior angles of regular polygons To solve problems involving angle measures of polygons Define Polygons A closed figure Formed by segments Polygons vs. Not Polygons Regular Polygon Convex polygon where all sides and angles are congruent. Types of Polygons A Convex polygon is a polygon such that no lines containing a side of the polygon contains a point in the interior of the polygon ~Angles face out A Concave polygon is a polygon for which there is a line containing a side of the polygon and a point in the interior of the polygon. ~ Angles cave in Convex or Concave Possible Diagonals/Triangles: Find the sum of degrees Determine how many triangles a shape have by drawing diagonals. Each triangle is 180 degrees. Thm 6-1-1: Polygon Angle Sum Theorem Formula: S = 180 (n – 2) S= sum of the measures of interior angles N = number of sides Sum S = 180(n -2) S = 180(3-2) S = 180(1) S = 180 An interior angle I = S/n I = 180/3 I = 60 Thm6-1-2: Polygon Exterior Angle Sum Theorem The sum of the measures of the exterior angles is 360° To find one exterior angle use formula Formula: E = 360/ n E= measure of exterior angles N = number of sides E = 360/n E = 360/3 E = 120 Warm-Up: Polygons Number of sides: 6 Name Polygon: Hexagon Number of Triangles: (n- 2) = 4 Is polygon convex or concave. Find sum of the measures of interior angles: S = 180(n-2) 180(4)= 720 Find the measure of an interior angle I = Sum 720 = 120 n 6 Find measure of an exterior angle: E = 360 n 360 = 60 6 Twitter #polygonsproperties P. 397 Think and Discuss #1 Draw a concave pentagon and convex pentagon. Explain the difference between the two figures. Textbook p. 395 Convex Polygons Number of Sides Number of triangles Sum of Angles Measures S = 180(n – 2) Measure of an Exterior Angle Ext = 360/n Triangle Quadrilateral Pentagon Hexagon Heptagon Octagon Nonagon Decagon Hendecagon Dodecagon n - gon n (n – 2) S = 180( n – 2) Ext = 360 / n Practice Geo: Textbook page 398 # 1- 15 Warm-Up: Polygons Number of sides: 7 Name Polygon: Heptagon Number of Triangles: (n- 2) = 5 Is polygon convex or concave. Find sum of the measures of interior angles: S = 180(n-2) 180(5)= 900 Find the measure of an interior angle I = Sum 900 = 128.57 n 7 Find measure of an exterior angle: E = 360 n 360 = 51.43 7 Warm Up: Part 2 Solve each proportion. 1. x = 11 2. 13 = 26 5 35 49 7x 3. x-2 = 3 x 8 Cross Multiply Cross Multiply Cross Multiply - 35(x) = 11(5) - 13(7x) = 49(26) - 8(x-2) = 3(x) - 35x = 55 91x = 1274 - 8x -16 = 3x - 35x = 55 35 35 - x = 1.57 - 91x = 1274 91 91 - x = 14 - 8x -8x -16 = 3x – 8x - -16 = -5x - -16 = -5x -5 -5 - x = 3.2 Practice Geo: Textbook page 398 # 1- 15 Chapter 7: Connecting Proportion and Similarity Recognize and use ratios and proportions Identify similar figures and use the proportions of similar figures to solve problems Use proportional parts of triangles to solve problems Exploring Similar Polygons Book Definition: Two polygons are similar if and only if their corresponding angles are congruent and the measures of their corresponding sides are proportional. Symbol: In simpler terms: Two polygons with the same shape but are different sizes. Are two congruent figures similar? Think about it…. Discuss… Yes, congruent figures have congruent angles and sides are proportional at 1:1 ratio Scale Factor and Dilation Dilation is a transformation that reduces or enlarges figures On a camera: zoom-in/ zoom-out Scale Factor = ______ A 5 D 2.5 4 B 3 C 10 =8 =6 = 5 5 4 3 2.5 E 10 H 5 dfgff 8 F 6 G Scale Factor Scale Factor = _____ 12 =9 = 24 4 3 8 4 Scale Factor = ______ A 6 D 2 5 8 B 3 12 24 4 C 12 =8 =7 =4 6 5 4 2 E 12 H 4 dfgff 8 9 F 7 G Similar Triangles: Property 1 Side-Side-Side Similarity __________________________: the three sides if _____________________ of one triangle are proportional the three corresponding sides ____________ to __________________________ of similar another triangle, then the triangles are ____________. Ex. Similar Triangles: Property 2 Angle - Angle Similarity _________________________: two angles of ___________ one triangle If the measures of ___________ congruent to 2 angles of the other are __________________________________ similar then the triangles are __________. Ex. Similar Triangles: Property 3 Side-Angle-Side Similarity ________________________: two sides of a triangle are ___________ proportional if the measures of __________ two sides of another triangle and the to the measures of _________ included angles are _________, congruent then the triangles are _________ similar ___________. Ex. Similarity Ratio: Triangle Proportionality Theorem VW = VX WY XZ Similarity Ratio: AE = AD = ED AC AB CB Similarity Ratio: EC = ED = CD EA EB AB X Solve for x and y. 49 29 x 20 y+3 21 Warm- up: 1. Draw a convex heptagon. 2. Draw a concave nonagon 3. Sketch a regular hexagon. Sum of interior angles: S = 180(6-2) = 720 I = 720/6 = 120 An Interior angle: An Exterior angle: E = 360/6 = 60 Check Practice: Similar Figures Notes: Sides are proportional & angles are congruent. P. 520 # 5, 6, 12, 13, 16, 17, 19 Quiz Time 10 mins Absolutely NO TALKING during quiz. Take your time Good LUCK! Practice Find a partner. Complete “How Can You Tell Which End of a Worm Is His Head?” (must complete in pairs). Each partner complete a side For each answer, write in letter of question. EACH SIDE IS DIFFERENT! Each partner must show work to receive FULL CREDIT. Use notebook paper Chapter 7: Practice Warm-Up 1. Use the Interior Angle Theorem to find measure of each angle. C B 3x-12 4x-14 A 7x +5 2. Are two congruent figures similar? Explain. 3. Quadrilaterals ABCD and AEFG are similar. AE=22, AB=5x + 4, EF=8 and BC=2x-2. Solve for x. A E B 5x -15 D 5x E G D F C Warm -Up 16 22 11 m 3 8 4 x 4 Warm up 1. Similar? Yes or No a. 4 6 b. 7 6 8 2. What is the difference between concave and convex polygons? 3. regular heptagon, find each. A. Sum of I = B. I= C. E= D. Sum of E= 1.8 1.4 1.3 15 20 5 12.5 Constructions Materials: paper, ruler and protractor Construct each (use polygon chart) Regular Pentagon ~ sides 3 inches Regular Octagon ~ sides 2 inches Your Choice ~ Regular Polygon ~ make sides a reasonable measure To start… find the measure of one interior angle. Draw one measured side with ruler. Next use protractor to measure angle Then draw 2nd side Repeat steps. Practice: Constructions Construct each (use polygon chart) Materials: paper, ruler and protractor Include the sum of interior angles and the measure of one interior angle Regular Pentagon ~ sides 3 inches Regular Octagon ~ sides 2 inches Your Choice ~ Regular Polygon (4+ sides) ~ make sides a reasonable measure Bonus: Your Choice ~ Regular Polygon (4+ sides) ~ make sides a reasonable measure To start… Draw one measured side with ruler. Next find the measure of one interior angle and use protractor to measure interior angle Then draw 2nd side Repeat steps. Warm up 1. Similar? Yes or No a. 4 6 b. 7 6 8 2. What is the difference between concave and convex polygons? 3. regular heptagon, find each. A. Sum of I = B. I= C. E= D. Sum of E= 1.8 1.4 1.3 15 20 5 12.5 Bonus 1. Draw if needed. Joyce sighted to the top of a tree along a stake that she knew to be 3 feet high. If she is standing 2 feet from the stake and 18 feet from the tree, how high is the tree? 2. Find x. 2x+32 8x+5 10x+2 12x+3 4x+12 4x+2 3. The lengths of the sides of a triangle are 3, 4, and 6. If the length of the shortest side of a similar triangle is 5, find the lengths of its other two sides.