Download CARNOT CYCLE i) substance starts at with temperature T2

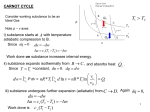
CARNOT CYCLE
Consider working substance to be an
Ideal Gas
Note p – v axes
i) substance starts at with temperature T2,
adiabatic compression to B.
Since
Work done on substance increases internal energy.
ii) substance expands isothermally from
Since
=constant,
and absorbs heat
.
P dv =
iii) substance undergoes further expansion (adiabatic) from
Work done is
Again
1
iv) substance returns to original point
by undergoing an isothermal compression
from D A , and the heat exhausted is equal to Q2.
Since du=0 for this isothermal process, dq = dw:
or
Since the working substance returns to its original state, the work done by the
substance is equal to the net heat absorbed, Q1-Q2
Work done = Q1-Q2
(area inside the “rectangle”)
This can be readily verified by summing the individual work terms.
This can be easily verified by adding up the individual terms.
Efficiency of the carnot cycle is
Q: How can
efficiency be
increased?
2
Only by transferring heat from a warm body to a cold body can heat be converted to work in a cyclic process.
For a CARNOT CYCLE
Proof: It can be shown that
= constant for adiabatic process
Adiabatic legs
For A
B
For C
D
Isothermal legs
For B
C
For D
A
Combining 4 equations
We already know that
3
maximum (Carnot) efficiency of a power cycle
Therefore
So
η = 1−
Q2
T
T
= 1− 2 = 1− cold
Q1
T1
Twarm
•  The maximum efficiency of an energy cycle is given by the Carnot efficiency, which
can be expressed as:
η€
= 1−
Tc
Th
If we consider the temperature difference between the equator and the poles:
Tpole
€ (Tc)
Tequator (Th)
We note that Th varies little throughout
the year (estimate as ~301 K), compared
with Tc
Winter hemisphere: estimate Tc ~ 263 K
η = 1−
Tc
263
= 1−
≈ 13%
Th
301
Summer hemisphere: estimate Tc ~ 283 K
€
η = 1−
Tc
283
= 1−
≈ 6%
Th
301
--> More of the absorbed energy is converted into “work” in the winter hemisphere
4
The hurricane as an energy cycle
Consider a hurricane as a Carnot cycle:
http://apollo.lsc.vsc.edu/classes/met130/notes/chapter15/vertical_circ.html
3
Toutflow
4
2
1
Tsea surface
Analyze each leg of the cycle:
1: absorption of energy from ocean, ~isothermal expansion
2: convection in the eyewall, ~adiabatic expansion
3: upper level outflow, ~ isothermal compression (reject heat via radiation)
4: sinking branch, ~adiabatic compression
If we estimate SST~300 K, and outflow T~200 K,
η = 1−
Tc
200
= 1−
≈ 30%
Th
300
U Hawaii class notes: Latent heat released when water vapor condenses in clouds is the key. Hurricanes are giant engines that
convert heat into wind energy. Consider a rain rate of 2 inches per day over an area of 300 mi radius: Over a 7 day lifecycle, the
energy released is equal to 50,000 1 MT nuclear explosions, equivalent to the total explosive yield of the nuclear arsenals of the
US and USSR at the height of the Cold War! www.soest.hawaii.edu/MET/Faculty/businger/.../18cHurricanes1.pdf
€
Our next state function: ENTROPY (consequence of Second Law)
There exists a function called entropy S, of the extensive variables of a system, defined for
all equilibrium states, such that the values assumed by the extensive variables are those
that maximize S (at equilibrium)
From the viewpoint of classical thermodynamics, entropy is defined as
where in this case heat is added to a substance undergoing a reversible transformation.
Clausius (1822-1888) stated that the cyclic integral of δQ/T is always less than or equal to zero:
∫
δQ
≤0
T
The cyclic integrals of work and of heat are not zero (engines).
Entropy is a STATE VARIABLE. (We can make up an internally reversible path from A to B to
compute change in entropy€
from the integral of δQ/T.)
Since dq= Tds, the First Law can be written as,
Tds = du + pdv
€
Even though we imagined a reversible
process to substitute for dq, this equation
applies to both reversible and irreversible
transitions because they are state variables
Generalized Statement of the Second Law
•  We need to generalize the definition of entropy since real systems are typically spontaneous
and irreversible, moving from a state of non-equilibrium to a state of equilibrium.
•  Second law can be formulated as 4 postulates:
1.  There exists a STATE VARIABLE for any substance called the ENTROPY.
2.  Entropy (S) may change by one of two ways; the substance may contact a thermal reservoir (heat
source), or S may change due to “internal” changes in the substance.
dse (externally-forced changes in S)
dsi (internally-forced changes in S)
Examples: dse Heat flow into a substance causing molecules to rearrange
dsi Mixing a gas, forcing molecules to change position.
Total entropy change ds = dse + dsi
3.  Changes in S due to external influences are given by
where dq = heat imported or exported, while substance is in
contact with a thermal reservoir at temperature
• 
4.  For reversible transformations,
For irreversible transformations,
So reversible and irreversible processes are distinguished by entropy changes. For reversible
processes, there are no entropy changes associated with internal processes, or they have ceased as the
system undergoes only reversible changes, say via contact with a heat reservoir.
Now consider the system + its surroundings ( = “universe”)
• 
In a reversible process any heat flow between the system and surroundings
must occur with no finite temperature difference between the system and
surroundings.  Otherwise the process would be irreversible
UNIVERSE
Since
• 
• 
Therefore
for reversible process.
As expected and can be shown via a similar argument,
Irreversible process
In general
Statement of 2nd Law!
Calculations of Entropy Changes
• 
For reversible processes,
• 
For irreversible processes,
• 
However since S is a state function,
depends only upon endpoints.
Hence
can be found by devising a series of reversible transformations
that are equivalent to the irreversible transformations.
is not necessarily equal to
1. Reversible adiabatic process
Hence
, hence
2. Reversible phase change at constant T, p
since
constant
where m=mass, L= latent heat
3. Reversible, isothermal process
4. Reversible change of state for an Ideal Gas
From First Law:
then
Heating term
Volume term
5. Constant-pressure heating (irreversible)
For constant pressure:
Hence
for
6. Similarly, for constant-volume heating (irreversible)
dq rev = cv dT + pdv
pdv → 0
T2
ΔS = ∫ cv ln dT
T1
⎛ T2 ⎞
ΔS = cv ln⎜ ⎟
⎝ T1 ⎠
More entropy calculations at end of notes
“Thermodynamic Potentials”
• 
The internal energy, when expressed as a function of S and V, is one of the
so-called “thermodynamic potentials”. The differential of a thermodynamic
potential gives the first and second laws of thermodynamics combined:
du = dq − dw
du = Tds − Pdv
• 
• 
• 
• 
S and V are the “native variables” for U (although we can express U as a
function of any two variables)
Remember €
enthalpy is:
H = U + PV
dh = Tds + vdP
So S and P are the “native variables” for H.
We define two more thermodynamic potentials that have “native variables” ,
respectively, of T and V and T and P.
€
 Very useful for equilibrium calcs!
Helmholtz & Gibbs Functions
• 
Consider the following system/reservoir arrangement,
Q
system
• 
-Q
Total work done by the system, whether it be in a reversible or irreversible
process is,
First Law
• 
reservoir
Q is positive if it flows into the
system
(1)
w is positive if done by the
system
dq=du+dw
From principle of entropy,
w=Q-(u2-u1)
(2)
A general expression
that entropy must stay
constant or increase
• 
For the reservoir,
heat flow out of reservoir
• 
Therefore we have
• 
• 
Note T= constant; reservoir has infinite heat capacity.
From (3) we have the following inequality,
• 
From First Law or Eq (1) above (substitute for Q)
(3)
Reversible process
Irreversible process
• 
For the irreversible case the work done is less than
since some of the
heat added to the system can go into changing the ‘internal’ entropy of the system.
(4)
• 
The difference in this energy between 2 equilibrium states at the same
temperature is
(5)
• 
Hence change in F sets an upper limit to the work that can be done in
any process between 2 equilibrium states at constant T.
• 
F is often referred to as the ‘free energy’ since ∆F represents the maximum
amount of work that can be done in a transformation at constant
temperature.
•  Returning to the equation
(6)
•  This equation is general and can be applied to any system, change
of state, phase, or even a chemical reaction.
•  In general, work in processes we are considering consist of pdV
work and other possible forms of work, e.g. work required to form a
curve interface between 2 phases, frictional dissipation, etc.
•  Let
represent pdV type work and
work, so we now have
represent other forms of
(7)
•  If we consider a constant volume process,
•  Hence at constant T and V, Helmholtz energy sets an upper limit
to the non- pdV work that can be done in such a transition.
• 
For a reversible constant volume process
• 
Now consider a situation where no pdV and no
work is done, then
•  Hence for a process at constant volume, for which
(and
T=constant), F can only decrease or remain constant. A transition
will not occur if
.
Wikipedia definition:
du = Tds − Pdv
The Helmholtz free energy is a thermodynamic
potential which measures the “useful” work
dh = Tds + vdP
obtainable from a closed thermodynamic system at a
f = u −Ts (by definition)
constant temperature and volume. For such a
system, the negative of the difference in the
df = du −Tds − sdT
Helmholtz energy is equal to the maximum amount
of work extractable from a thermodynamic process in
= −sdT − Pdv
which temperature and volume are held constant.
Under these conditions (constant T and v), it is
Constant v constraint is not
minimized at equilibrium.
(8)
always helpful for us …
€
• 
Next, consider a process that occurs at constant pressure. In this case the
pdV work is
• 
Then returning to the equation:
• 
We have:
(8)
Now define the Gibbs Free Energy as,
(dG = -SdT + VdP)
Then for a transition between 2 states at the same T ,p:
and substituting into (8) we have
∆G represents the total non- pdV work for a constant T,P process. This
is of fundamental importance for cloud physics.
quick look ahead to one application we’ll be discussing:
• 
• 
• 
During nucleation, some energy is released when molecules move from the
vapor to the “liquid” phase
is the work (energy required) necessary to form the surface of the small
liquid (or ice) embryo from the vapor phase:
If
So G can only decrease in a transition occurring at constant T, P.
• 
If the hypothetical nucleus is too small (known as an unstable nucleus or "embryo"),
the energy that would be released by forming its volume is not enough to create its
surface
Thermodynamic Potential
• 
• 
• 
Given
Consider a closed system which is one where no mass is allowed to cross
the boundaries of the system.
Taking total differentials,
(1)
(2)
• 
Using First Law in the form:
• 
We can substitute for (1) and (2) the dU term
• 
Consider the following series of equations,
• 
It is useful to identify the coefficients of the equations on the left hand side
with partial derivatives of the variables on the right hand side.
• 
For:
• 
Therefore we have
• 
Since
• 
Therefore
• 
Since
• 
And
• 
Since
• 
And
• 
Since P, V, T and S can be expressed as partial derivatives of U, F, G and
H, the latter variables are referred to as Thermodynamic Potentials.
Maxwell Relations
•  The “Gibbs relations” are the following equations that we have already seen:
du = Tds − Pdv
dh = Tds + vdP
da = −sdT − Pdv
dg = −sdT + vdP
•  We recognize that they are exact differentials and have the form
€
dz = Mdx + Ndy
⎛ ∂M ⎞ ⎛ ∂N ⎞
⎜
⎟ = ⎜ ⎟
⎝ ∂y ⎠ x ⎝ ∂x ⎠ y
•  We can deduce the “Maxwell Relations”:
⎛ ∂€T ⎞
⎛ ∂P ⎞
⎜ ⎟ = −⎜ ⎟
⎝ ∂v ⎠ s
⎝ ∂s ⎠ v
⎛ ∂T ⎞ ⎛ ∂v ⎞
⎜ ⎟ = ⎜ ⎟
⎝ ∂P ⎠ s ⎝ ∂s ⎠ P
⎛ ∂s ⎞ ⎛ ∂P ⎞
⎜ ⎟ = ⎜ ⎟
⎝ ∂v ⎠T ⎝ ∂T ⎠ v
⎛ ∂s ⎞
⎛ ∂v ⎞
⎜ ⎟ = −⎜ ⎟
⎝ ∂P ⎠T
⎝ ∂T ⎠ P
Can get
unmeasurables in
terms of measurables
Stable and Unstable Equilibrium
• 
• 
Stable Equilibrium: a state in which all irreversible processes have ceased,
and the system is in a state of maximum entropy. Reversible
transformations are possible (for which
).
For state equilibrium,
MAX
ENTROPY
• 
• 
a) 
This equilibrium condition is for an isolated system (no heat transfer, no
mass transfer)
A typical system we will deal with is NOT in thermal isolation, but rather in
contact with a heat reservoir (e.g., as approximated by the atmosphere).
For a transition at constant volume, in thermal contact with a reservoir at
temperature T, the stable state is defined by,
Helmholtz free energy is a minimum
b)
For a transition at constant pressure and temperature, (in contact with a
thermal reservoir), stable state is,
Gibbs free energy is a minimum
Applying equilibrium criteria
•  We can now add moisture to the air parcel we’ve computed changes
for
–  We could have added water to the “dry air mixture” and computed a
new average molecular weight, etc., BUT we know that simple
approach, assuming water stays as a vapor during the adiabatic ascent,
is only valid over small regions
–  That is, we’ll need to consider phase changes for the water
•  First, we’ll figure out where vapor, liquid and ice are in equilibrium,
and the energy changes associated with the transitions
–  Can calculate changes such as heat released so we can treat the
energy changes in our parcel
–  Can also figure out if the change is favored (e.g., if the transition is
allowed to occur thermodynamically, given specified conditions)
LATENT HEATS:
During a phase change, the pressure is constant and equal to the saturation pressure
(which is a function of T only). Adding heat to a substance at constant pressure and
resulting in a change in physical state, i.e. change in phase, is
described by,
Starting with First Law in the
dq = dh = Ldm
form dq = dh when dp = 0
where L is the latent heat (J kg-1) for the particular transition and m is mass
transferred between phases. The heat absorbed goes into changing the
molecular configuration/structure. For water substance:
€
Heat of fusion
L is an energy change to
go from one phase to
another
Heat of condensation
Heat of sublimation
SOLID
Lf
LIQUID
Lc
VAPOR
26
LS
Thermodynamics of Moist Air
• 
Phase transitions: what are the equilibrium conditions for a mixed-phase
system, e.g. a mixture of water and water vapor?
• 
Consider a system consisting of liquid water and H2O(v) undergoing a
change in state,
vapor
vapor
liquid
liquid
″ denotes liquid phase
″′ denotes vapor phase
• 
Define
• 
Hence
• 
Since both states are stable equilibrium states, G1=G2,
and therefore
n1ʹ′ʹ′gʹ′ʹ′ + n1ʹ′ʹ′gʹ′ ʹ′ʹ′ʹ′ = n ʹ′2ʹ′gʹ′ʹ′ + n ʹ′2ʹ′ʹ′gʹ′ʹ′ʹ′
But since the system is closed
( n1ʹ′ʹ′ − n ʹ′2ʹ′) gʹ′ʹ′ = ( n ʹ′2ʹ′ʹ′ − n1ʹ′ʹ′ʹ′) gʹ′ʹ′ʹ′
Therefore
• 
• 
n1ʹ′ʹ′ + n1ʹ′ʹ′ʹ′= n ʹ′2ʹ′ + n ʹ′2ʹ′ʹ′
n ʹ′2ʹ′ = n1ʹ′ʹ′ + n1ʹ′ʹ′ʹ′− n ʹ′2ʹ′ʹ′
• 
• 
• 
At equilibrium, the specific Gibbs free energy is the same for both phases
At the triple point,
Lets look at g between 2 phases in more detail:
vapor
c
g
liquid
b,e
f
d
a
T
• 
From earlier discussions,
• 
Where s′″ is the specific entropy of the vapor phase. Hence the slope of
gives the specific entropy.
Likewise
for the liquid phase
• 
• 
Note the slopes are <0, since larger values of g correspond to lower T’s. The
difference between entropies is
• 
Since
vapor
liquid
vs. T
Clausius-Clapeyron Equation
• 
This equation is very important since it describes the variation in pressure
with temperature, for a system consisting of two phases in
equilibrium. For the case of a liquid/vapor or vapor/solid system, this
“pressure” is the saturation vapor pressure.
vaporʹ′ʹ′ʹ′
liquid ʹ′ʹ′
• 
For a system in equilibrium,
• 
€
Suppose the system undergoes a small change to a new pressure and
temperature, p+dp, T+dT such that the new state is also a stable state.
Each phase changes by
amounts.
Then for each phase:
• 
Since the new state is also an equilibrium state,
• 
• 
Or,
s, v are specific
quantities!
CLAUSIUS-CLAPEYRON
EQUATION
• 
Since
=latent heat for vapor-liquid interface
For vapor-liquid system
• 
• 
• 
For vapor-liquid system
For vapor-ice system
Geometrical Interpretation
SOLID
LIQUID
S-L
L-V
P
Triple point
Critical point
S-V
VAPOR
T
gives the slope of the
equilibrium line between
the 2 phases involved.
(on P-V-T diagram.)
• 
Looking again at the Clausius-Clapeyron Equation we have three interfaces,
vaporliquid
solidvapor
liquidsolid
• 
1. 
Since
always, the slope of the equilibrium line between the 2
phases involved is determined by the difference in specific volumes.
vaporliquid
vaporsolid
] ALWAYS
For all materials!
2.
For substance that expands upon freezing (like water). Hence
P
L
S
Triple
V
T
substance contracts upon freezing.
MOST SUBSTANCES!
• 
Integrate the Clausius-Clapeyron Eqn/ to get es as a function of T. For a
vapor/liquid system,
• 
Assume
GAS LAW
• 
Therefore
after integration
More entropy calculations
35
Rapid expansion
7. Irreversible change of state of an Ideal Gas
Let n moles of an ideal gas of
irreversibly change state to
This irreversible process can be broken into 2 reversible processes:
1.) A slow expansion to
at constant
-put gas in a frictionless piston-cylinder, place in constant temperature
bath; slowly move piston out
2.) Hold gas at
, heat gas to temperature
and pressure
Hence
Constant-volume heating
Isothermal expansion
8. Irreversible phase change
Let 10g of supercooled water at -10°C change to ice at -10°C. Consider
constant pressure.
This process is IRREVERSIBLE e.g. if the ice is slowly heated, it will not
become water at -10°C.
Water at -10°C
IRREVERSIBLE
Ice at -10°C
1
Water at 0°C
3
2
Ice at 0°C
Find equivalent reversible path and compute entropy change
1.) Isobaric heating of water
2.) Phase change
3.) Isobaric cooling of ice
More entropy calculations
• 
Calculate the change in entropy when 5g of water at 0°C are raised to
100°C and converted into vapor (steam) at that temperature.
1. Raise temperature of H2O(l) from 0°C to 100°C
Let
Specific heat of water
2. Convert to vapor (steam) at 100°C
• 
Find
for the melting of 5g of ice at 0°C at 1 atm.
This process is reversible since both ice and liquid states are possible at
0°C. (Equilibrium states!)
• 
For freezing of liquid water,
and
Why the specific signs for melting vs. freezing?
• 
Let n moles of a perfect gas undergo an adiabatic free expansion into a
vacuum (this is Joule’s experiment).
–  Express ∆S in terms of the initial and final temperature and volume.
–  Calculate ∆S if
• 
The initial state is
and the final state is
Although the process is adiabatic, (dq=0), entropy change is non-zero
because this process is irreversible. Entropy of course changes (and
increases) since the molecules changed their configuration expanding into
the vacuum.
Hence
With
This is the so-called Entropy of Mixing.