Download FUNDAMENTAL THEORY OF LOAD COMPENSATION

Chapter 3
FUNDAMENTAL THEORY OF LOAD
COMPENSATION
(Lectures 19-28)
3.1
Introduction
In general, the loads which have poor power factor, unbalance, harmonics, and dc components
require compensation. These loads are arc and induction furnaces, sugar plants, steel rolling mills
(adjustable speed drives), power electronics based loads, large motors with frequent start and stop
etc. All these loads can be classified into three basic categories.
1. Unbalanced ac load
2. Unbalanced ac + non linear load
3. Unbalanced ac + nonlinear ac + dc component of load.
The dc component is generally caused by the usage of half-wave rectifiers. These loads, particularly nonlinear loads generate harmonics as well as fundamental frequency voltage variations.
For example arc furnaces generate significant amount of harmonics at the load bus.
Other serious loads which degrade power quality are adjustable speed drives which include power
electronic circuitry, all power electronics based converters such as thyristor controlled drives, rectifiers, cyclo converters etc.. In general, following aspects are important, while we do provide the
load compensation in order to improve the power quality [1].
1. Types of load (unbalance , harmonics and dc component)
2. Real and Reactive power requirements
3. Rate of change of real and reactive power etc.
In this unit, we however, discuss fundamental load compensation techniques for unbalanced linear
loads such as combination of resistance, inductance and capacitance and their combinations. The
objective here will be to maintain currents balanced and unity factor with their voltages.
69
3.2
Fundamental Theory of Load Compensation
We shall find some fundamental relation ship between supply system the load and the compensator.
We shall start with the principle of power factor correction, which in its simplest form, and can be
studied without reference to supply system [2]–[5].
The supply system, the load and the compensator can be modeled in various ways. The supply
system can be modeled as a Thevenin’s equivalent circuit with an open circuit voltage and a series impedance, (its current or power and reactive power) requirements. The compensator can be
modeled as variable impedance or as a variable source (or sink) of reactive current. The choice of
model varied according to the requirements. The modeling and analysis done here is on the basis
of steady state and phasor quantities are used to note the various parameters in system.
3.2.1
Power Factor and its Correction
Consider a single phase system shown in 3.1(a) shown below. The load admittance is represented
Is
V
l
IX
IR
V
Il
Il
Fig. 3.1 (a) Single line diagram of electrical system (b) Phasor diagram
by Yl = Gl + jBl supplied from a load bus at voltage V = V ∠0. The load current is I l is given as,
I l = V (Gl + jBl ) = V Gl + jV Bl
= IR + jIX
(3.1)
According to the above equation, the load current has a two components, i.e. the resistive or in
phase component and reactive component or phase quadrature component and are represented by
IR and IX respectively. The current, IX will lag 90o for inductive load and it will lead 90o for
capacitive load with respect to the reference voltage phasor. This is shown in 3.1(b). The load
apparent power can be expressed in terms of bus voltage V and load current Il as given below.
Sl =
=
=
=
=
=
V (Il )∗
V (IR + j IX )∗
V (IR − j IX )
V (Il cos φl − j Il sin φl )
V Il cos φl − j V Il sin φl
Sl cos φl − j Sl sin φl
70
(3.2)
From (3.1), I l = V (Gl + jBl ) = V Gl + jV Bl , equation (3.2) can also be written as following.
Sl =
=
=
=
=
V (Il )∗
V (V Gl + jV Bl )∗
V (V Gl − jV Bl )
V 2 Gl − j V 2 Bl
Pl + jQl
(3.3)
From equation (3.3), load active (Pl ) and reactive power (Ql ) are given as,
Pl = V 2 Gl
Ql = −V 2 Bl
(3.4)
Now suppose a compensator is connected across the load such that the compensator current, Iγ is
equal to −IX , thus,
I γ = V Yγ = V (Gγ + jBγ ) = −IX
= −j V Bl
(3.5)
The above condition implies that Gγ = 0 and Bγ = −Bl . The source current Is , can therefore
given by,
I s = I l + Iγ = IR
(3.6)
Therefore due to compensator action, the source supplies only in phase component of the load
current. The source power factor is unity. This reduces the rating of the power conductor and
losses due to the feeder impedance. The rating of the compensator is given by the following
expression.
S γ = Pγ + j Qγ = V (I γ )∗
= V (−j V Bl )∗
= jV 2 Bl
(3.7)
Using (3.4), the above equation indicates the Pγ = 0 and Qγ = − Ql . This is an interesting
inference that the compensator generates the reactive power which is equal and opposite to the
load reactive and it has no effect on active power of the load. This is shown in Fig. 3.2. Using
(3.2) and (3.7), the compensator rating can further be expressed as,
Qγ = −Ql = −Sl sin φl = −Sl
p
1 − cos2 φl VArs
(3.8)
From (3.8),
|Qγ | = Sl
p
1 − cos2 φl
(3.9)
If |Qγ | < |Ql | or |Bγ | < |Bl |, then load is partially compensated. The compensator of fixed
admittance is incapable of following variations in the reactive power requirement of the load. In
71
I  I X
Is
V
Is  IR
l
IX
I
Il
Il
Fig. 3.2 (a) Single line diagram of compensated system (b) Phasor diagram
practical however a compensator such as a bank of capacitors can be divided into parallel sections,
each of switched separately, so that discrete changes in the reactive power compensation can be
made according to the load. Some sophisticated compensators can be used to provide smooth and
dynamic control of reactive power.
Here voltage of supply is being assumed to be constant. In general if supply voltage varies, the
Qγ will not vary separately with the load and compensator error will be there. In the following
discussion, voltage variations are examined and some additional features of the ideal compensator
will be studied.
3.2.2
Voltage Regulation
Voltage regulation can be defined as the proportional change in voltage magnitude at the load bus
due to change in load current (say from no load to full load). The voltage drop is caused due to
feeder impedance carrying the load current as illustrated in Fig. 3.3(a). If the supply voltage is
represented by Thevenin’s equivalent, then the voltage regulation (VR) is given by,
E − V E − |V |
VR =
(3.10)
=
V |V |
for V being a reference phasor.
In absence of compensator, the source and load currents are same and the voltage drop due to the
feeder is given by,
∆V = E − V = Zs Il
(3.11)
The feeder impedance, Zs = Rs + jXs . The relationship between the load powers and its voltage
and current is expressed below.
S l = V (I l )∗ = Pl + jQl
(3.12)
Since V = V , the load current is expressed as following.
Il =
Pl − jQl
V
72
(3.13)
Substituting, Il from above equation into (3.11), we get
Pl − jQl
∆V = E − V = (Rs + jXs )
V
Rs Pl + Xs Ql
Xs Pl − Rs Ql
=
+j
V
V
= ∆VR + j∆VX
(3.14)
Thus, the voltage drop across the feeder has two components, one in phase (∆VR ) and another is
in phase quadrature (∆VX ). This is illustrated in Fig. 3.3(b).
Feeder
E
Z s  Rs  jX s
E
Is
l
Load
V
Il
j VX

VR
V
R Il
Yl  Gl  jBl
jX l I l
Il
Sl  Pl  jQl
Fig. 3.3 (a) Single phase system with feeder impedance (b) Phasor diagram
From the above it is evident that load bus voltage (V ) is dependent on the value of the feeder
impedance, magnitude and phase angle of the load current. In other words, voltage change (∆V )
depends upon the real and reactive power flow of the load and the value of the feeder impedance.
Now let us add compensator
in
parallel
with the load as shown in Fig. 3.4(a). The question is:
whether it is possible to make E = V , in order to achieve zero voltage regulation irrespective of
change in the load. The answer is yes, if the compensator consisting of purely reactive components,
has enough capacity to supply to required amount of the reactive power. This situation is shown
using phasor diagram in Fig. 3.4(b).
The net reactive at the load bus is now Qs = Qγ + Ql . The compensator
reactive power (Qγ ) has
to be adjusted in such a way as to rotate the phasor ∆V until E = V .
From (3.14) and Fig. 3.3(b),
Rs Pl + Xs Qs
Xs Pl − Rs Qs
E∠δ = V +
+j
V
V
(3.15)
The above equation implies that,
2 2
Rs Pl + Xs Qs
Xs Pl − Rs Qs
2
E =
V +
+
V
V
(3.16)
73
Feeder
E
Z s  Rs  jX s
I
Il
I
V
Load
Q
Comp.
Is
E
Is
l
Yl  Gl  jBl
Sl  Pl  jQl
V

V
jX s I s
Rs Is
Il
Fig. 3.4 (a) Voltage with compensator (b) Phasor diagram
The above equation can be simplified to,
E 2 V 2 = (V 2 + Rs Pl )2 + Xs2 Q2s + 2(V 2 + RsPl ) Xs Qs
(
((
+Xs2 Pl2 + Rs2 Q2s − (
2X
P(
(s(
l Rs Qs
(3.17)
Above equation, rearranged in the powers of Qs , is written as following.
(Rs2 + Xs2 ) Q2s + 2V 2 Xs Qs + (V 2 + Rs Pl )2 + (Xs Pl )2 − E 2 V 2 = 0
(3.18)
Thus the above equation is quadratic in Qs and can be represented using coefficients of Qs as given
below.
a Q2s + b Qs + c = 0
(3.19)
Where a = Rs2 + Xs2 , b = 2V 2 Xs and c = (V 2 + Rs Pl )2 + Xs2 Pl2 − E 2 V 2 .
Thus the solution of above equation is as following.
p
−b ± (b2 − 4ac)
Qs =
(3.20)
2a
In the actual compensator, this value would be determined automatically by control loop. The
equation also indicates that, we can find the value of Qs by subjecting a condition such as E = V
irrespective of the requirement of the load powers (Pl , Ql ). This leads to the following conclusion
that a purely reactive compensator can eliminate supply voltage variation caused by changes in
both the real and reactive power of the load, provided that there is sufficient range and rate of Qs
both in lagging and leading pf. This compensator therefore acts as an ideal voltage regulator. It
is mentioned here that we are regulating magnitude of voltage and not its phase angle. In fact its
phase angle is continuously varying depending upon the load current.
It is instructive to consider this principle from different point of view. We have seen that compensator can be made to supply all load reactive power and it acts as power factor correction device.
If the compensator is designed to compensate power factor, then Qs = Ql + Qγ = 0. This implies that Qγ = −Ql . Substituting Qs = 0 for Ql in (3.14) to achieve this condition, we get the
74
following.
∆V
=
(Rs + jXs )
Pl
V
(3.21)
From above equation, it is observed that ∆V is independent of Ql . Thus we conclude that a purely
reactive compensator cannot maintain both constant voltage and unity power factor simultaneously.
Of course the exception to this rule is a trivial case when Pl = 0.
3.2.3
An Approximation Expression for the Voltage Regulation
Consider a supply system with short circuit capacity (Ssc ) at the load bus. This short circuit capacity can be expressed in terms of short circuit active and reactive powers as given below.
∗
E
E2
∗
S sc = Psc + jQsc = E I sc = E
= ∗
(3.22)
Zsc
Zsc
Where Zsc = Rs + jXs and I sc is the short circuit current. From the above equation
|Zsc | =
Therefore, Rs =
Xs =
tan φsc =
E2
Ssc
E2
cos φsc
Ssc
E2
sin φsc
Ssc
Xs
Rs
Substituting above values of Rs and Xs , (3.14) can be written in the following form.
∆V
Pl cos φsc + Ql sin φsc
Pl sin φsc − Ql cos φsc E 2
=
+j
V
V2
V2
Ssc
∆V
∆VR
∆VX
=
+j
V
V
V
Using an approximation that E ≈ V , the above equation reduces to the following.
∆V
Pl cos φsc + Ql sin φsc
Pl sin φsc − Ql cos φsc
=
+j
V
Ssc
Ssc
The above implies that,
∆VR
Pl cos φsc + Ql sin φsc
≈
V
Ssc
∆VX
Pl sin φsc − Ql cos φsc
≈
V
Ssc
75
(3.23)
(3.24)
(3.25)
Often (∆VX /V ) is ignored on the ground that the phase quadrature component contributes negligible to the magnitude of overall phasor. It mainly contributes to the phase angle. Therefore the
equation (3.25) is simplified to the following.
∆VR
Pl cos φsc + Ql sin φsc
∆V
=
=
V
V
Ssc
(3.26)
Implying that the major change in voltage regulation occurs due to in phase component, ∆VR .
Although approximate, the above expression is quite useful in terms of short circuit level (Ssc ),
(Xs /Rs , active and reactive power of the load.
On the basis of incremental changes in active and reactive powers of the load, i.e., ∆Pl and ∆Ql
respectively, the above equation can further be written as,
∆V
∆VR
∆Pl cos φsc + ∆Ql sin φsc
=
=
.
V
V
Ssc
(3.27)
Further, feeder reactance (Xs ) is far greater than feeder resistance (Rs ), i.e., Xs >> Rs . This
implies that, φsc → 90o , sin φsc → 1 and cos φsc → 0. Using this approximation the voltage
regulation is given as following.
∆V
∆VR
∆Ql
∆Ql
≈
≈
sin φsc ≈
.
V
V
Ssc
Ssc
(3.28)
That is, per unit voltage change is equal to the ratio of the reactive power swing to the short circuit
level of the supply system. Representing ∆V approximately by E − V and assuming linear change
in reactive power with the voltage, the equation (3.28) can be writtwn as,
E−V
Ql
.
≈
V
Ssc
(3.29)
The above leads to the following expression,
V '
E
Ql
' E(1 −
)
Ql
Ssc
(1 + Ssc )
(3.30)
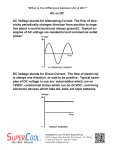
with the assumption that, Ql /Ssc << 1. Although above relationship is obtained with approximations, however it is very useful in visualizing the action of compensator on the voltage. The
above equation is graphically represented as Fig. 3.5. The nature of voltage variation is drooping
with increase in inductive reactive power of the load. This is shown by negative slope −E/Ssc as
indicated in the figure.
The above characteristics also explain that when load is capacitive, Ql is negative. This makes
V > E. This is similar to Ferranti effect due to lightly loaded electric lines.
Example 3.1 Consider a supply at 10 kV line to neutral voltage with short circuit level of 250
MVA and Xs /Rs ratio of 5, supplying a star connected load inductive load whose mean power is
25 MW and whose reactive power varies from 0 to 50 MVAr, all quantities per phase.
76
V
E

E
S sc
0
Ql
Fig. 3.5 Voltage variation with reactive power of the load
(a) Find the load bus voltage (V ) and the voltage drop (∆V ) in the supply feeder. Thus determine
load current (I l ), power factor and system voltage (E ).
(b) It is required to maintain the load bus voltage to be same as supply bus voltage i.e. V =10 kV.
Calculate reactive power supplies by the compensator.
(c) What should be the load bus voltage and compensator current if it is required to maintain the
unity power factor at the supply?
Solution: The feeder resistance and reactance are computed as following.
Zs = Es2 /Ssc = (10 kV)2 /250 = 0.4 Ω/phase
It is given that, Xs /Rs = tan φsc = 5, therefore φsc = tan−1 5 = 78.69o . From this,
Rs = Zs cos φsc = 0.4 cos(78.69o ) = 0.0784 Ω
Xs = Zs sin φsc = 0.4 sin(78.69o ) = 0.3922 Ω
(a) Without compensation Qs = Ql , Qγ = 0
To know ∆V , first the voltage at the load bus has to be computed. This is done by rearranging
(3.18) in powers of voltage V . This is given below.
(Rs2 + Xs2 ) Q2l + 2 V 2 Xs Ql + (V 2 + Rs Pl )2 + Xs2 Pl2 − E 2 V 2 = 0
(R2 + X 2 ) Q2 + 2 V 2 X Q + V 4 + R2 P 2 + 2 V 2 R P + X 2 P 2 − E 2 V 2 = 0
| s {z s }l | {z s }l |{z} | s{z l} | {z s }l | s{z l} | {z }
III
II
I
III
II
III
II
Combining the I, II and III terms in the above equation, we get the following.
V 4 + 2(Rs Pl + Xs Ql ) − E 2 V 2 + (Rs2 + Xs2 )(Q2l + Pl2 ) = 0
Now substituting values of Rs , Xs , Pl , Ql and E in above equation, we get,
V 4 + 2 [0.0784 × 25 + 0.3922 × 50] − 102 V 2 + (0.07842 + 0.39222 )(252 + 502 ) = 0
77
(3.31)
After simplifying the above, we have the following equation.
V 4 − 56.86V 2 + 500 = 0
Therefore
V
2
and V
√
56.86 − 4 × 500
=
2
= 45.985, 10.875
= ±6.78 kV, ±3.297 kV
56.86 ±
Since rms value cannot be negative and maximum rms value must be a feasible solution, therefore
V = 6.78 kV.
Now we can compute ∆V using (3.14), as it is given below.
∆V
R s Pl + X s Q l
Xs Pl − Rs Ql
+j
V
V
0.3922 25 − 0.0784 50
0.0784 25 + 0.392 50
+j
=
6.78
6.78
= 3.1814 + j0.8677 kV = 3.2976∠15.25o kV
=
Now the line current can be found out as following.
Pl − Ql
25 − j50
=
V
6.782
= 3.86 − j7.3746 kA
= 8.242∠ − 63.44o kA
Il =
The power factor of load is cos (tan−1 (Ql /Pl )) = 0.4472 lagging. The phasor diagram for this
case is similar to what is shown in Fig. 3.3(b).
(b) Compensator as a voltage regulator
Now it is required to maintain V = E = 10.0 kV at the load bus. For this let their be reactive power Qγ supplied by the compensator at the load bus. Therefore the net reactive power at the
load bus is equal to Qs , which is given below.
Qs = Ql + Qγ
Thus from (3.18), we get,
(Rs2 + Xs2 )Q2s + 2V 2 Xs Qs + (V 2 + Rs Pl )2 + Xs2 Pl2 − E 2 V 2 = 0
(0.7842 + 0.39222 )2 Q2s + 2 × 102 × 0.3922 × Qs + (102 + 0.784 × 25)2 + 0.39222 × 252 − 104 = 0
From the above we have,
0.16 Q2s + 78.44 Qs + 491.98 = 0.
78
Solving the above equation we get,
√
78.442 − 4 × 0.16 × 491.98
2 × 0.16
= −6.35 or − 484 MVAr.
Qs =
−78.44 ±
The feasible solution is Qs = −6.35 MVAr because it requires less rating of the compensator.
Therefore the reactive power of the compensator (Qγ ) is,
Qγ = Qs − Ql = −6.35 − 50 = −56.35 MVAr.
With Qs = −6.35 MVAr, the ∆V is computed by replacing Qs for Ql in (3.14) as given below.
∆V
Xs Pl − Rs Qs
Rs Pl + Xs Qs
+j
V
V
0.0784 × 25 + 0.39225 × −6.35
0.39225 × 25 − 0.0784 × (−6.35)
=
+j
10
10
1.96 − 2.4
9.805 + 0.4978
=
+j
10
10
= −0.0532 + j1.030 kV = 1.03137∠92.95o kV
=
Now, we can find supply voltage E as given below.
E = ∆V + V
= 10 − 0.0532 + j1.030
= 9.9468 + j1.030 = 10∠5.91o kV
The supply current is,
Pl − jQs
25 − j(−6.35)
=
V
10
= 2.5 + j0.635 kA = 2.579∠14.25o kA.
Is =
This indicates that power factor is not unity for perfect voltage regulation i.e., E = V . For this
case the compensator current is given below.
−jQγ
−j(−56.35)
=
V
10
= j5.635 kA
Iγ =
Iγ
The load current is computed as below.
Pl − jQl
25 − j50
=
V
10
= 2.5 − j5.0 = IlR + jIlX = 5.59∠63.44o kA
Il =
The phasor diagram is similar to the one shown in Fig. 3.4(b). The phasor diagram shown has
interesting features. The voltage at the load bus is maintained to 1.0 pu. It is observed that the
reactive power of the compensator Qγ is not equal to load reactive power (Ql ). It exceeds by 6.35
79
MVAr. As a result of this compensation, the voltage regulation is perfect, however power factor is
not unity. The phase angle between V and I s is cos−1 0.969 = 14.25o as computed above. Therefore the angle between E and I s is (14.25o − 5.91o = 8.34o ). Thus, source power factor (φs ) is
cos(8.340 ) = 0.9956 leading.
(c) Compensation for unity power factor
To achieve unity power factor at the load bus, the condition Qγ = −Ql must be satisfied, which
further implies that the net reactive power at the load bus is zero. Therefore substituting Ql = 0 in
(3.31), we get the following.
V 4 + 2(Rs Pl − E 2 ) V 2 + (Rs2 + Xs2 )(Pl2 + Q2l ) = 0
V 4 + (2 × 0.0784 × 25 − 102 )V 2 + (0.07842 + 0.39222 ) 252 = 0
From the above,
V 4 + 96.08V 2 + 99.79 = 0
The solution of the above equation is,
96.08 ± 93.97
= 95.02, 1.052
2
= ±9.747 kV, ±1.0256 kV.
V2 =
V
Since rms value cannot be negative and maximum rms value must be a feasible solution, therefore
V = 9.747 kV. Thus it is seen that for obtaining unity power factor at the load bus does not ensure
desired voltage regulation. Now the other quantities are computed as given below.
Il =
Pl − jQ
25 − j50
=
= 2.5648 − j5.129 = 5.7345∠−63.43o kA
V
9.747
Since Qγ = −Ql , this implies that Iγ = −jQγ /V = jQl /V = j5.129 kA. The voltage drop across
the feeder is given as following.
∆V
Rs Pl + Xs Ql
Xs Pl − Rs Ql
+j
V
V
(0.784 × 25 + j0.3922 × 25)
=
9.747
= 0.201 + j1.005 = 1.0249∠5.01o kV
=
The phasor diagram for the above case is shown in Fig. 3.6.
The percentage voltage change = (10 − 9.748)/10 × 100 = 2.5. Thus we see that power factor
improves voltage regulation enormously compared with uncompensated case. In many cases, degree of improvement is adequate and the compensator can be designed to provide reactive power
requirement of load rather than as a ideal voltage regulator.
80
I   j 5.13 kA
E 10 kV
5.77
VX
V = 9.75 kV VR
I lR = 2.56 kA
I lX   j 5.13 kA
Is
I l  5.73  63.43 kA
Fig. 3.6 Phasor diagram for system with compensator in voltage regulation mode
3.3
Some Practical Aspects of Compensator used as Voltage Regulator
In this section, some practical aspects of the compensator in voltage regulation mode will be discussed. The important parameters of the compensator which play significant role in obtaining
desired voltage regulation are: Knee point (V k ), maximum or rated reactive power Qγmax and the
compensator gain Kγ .
The compensator gain Kγ is defined as the rate of change of compensator reactive power Qγ
with change in the voltage (V ), as given below.
Kγ =
dQr
dV
(3.32)
For linear relationship between Qγ and V with incremental change, the above equation be written
as the following.
∆Qγ = ∆V Kγ
(3.33)
Assuming compensator characteristics to be linear with Qγ ≤ Qγmax limit, the voltage can be
represented as,
Qγ
V = Vk +
(3.34)
Kγ
This is re-written as,
Qγ = Kγ (V − Vk )
81
(3.35)
Flat V-Q characteristics imply that Kγ → ∞. That means the compensator which can absorb or
generate exactly right amount of reactive power to maintain supply voltage constant as the load
varies without any constraint. We shall now see the regulating properties of the compensator,
when compensator has finite gain Kr operating on supply system with a finite short circuit level,
Ssc . The further which are made in the following study are: high Xs /Rs ratio and negligible load
power fluctuations. The net reactive power at the load bus is sum of the load and the compensator
reactive power as given below.
Ql + Qγ = Qs
(3.36)
Using earlier voltage and reactive power relationship from equation (3.30), it can be written as the
following.
V ' E(1 −
Qs
)
Ssc
(3.37)
The compensator voltage represented by (3.34) and system voltage represented by (3.37) are shown
in Fig. 3.7(a) and (b) respectively.
V
V  Vk 
Q
K
Vk
E
 Q 
V  E 1- s 
 S SC 
Q
Qs
(a)
(b)
Fig. 3.7 (a) Voltage characterstics of compensator (b) System voltage characteristics
Differentiating V with respect to Qs , we get, intrinsic sensitivity of the supply voltage with
variation in Qs as given below.
dV
E
=−
(3.38)
dQs
Ssc
It is seen from the above equation that high value of short circuit level Ssc reduces the voltage
sensitivity, making voltage variation flat irrespective of Ql . With compensator replacing Qs =
Qγ + Ql in (3.37), we have the following.
Ql + Qγ
V 'E 1−
Ssc
82
(3.39)
Substituting Qγ from (3.35), we get the following equation.
Ql /Ssc
1 + Kγ Vk /Ssc
−
V 'E
1 + E Kγ /Ssc 1 + E Kγ /Ssc
(3.40)
Although approximate, above equation gives the effects of all the major parameters such as load
reactive power, the compensator characteristics Vγ and Kγ and the system characteristics E and
Ssc . As we discussed, V-Q characteristics is flat for high or infinite value Kγ . However the higher
value of the gain Kγ means large rating and quick rate of change of the reactive power with variation in the system voltage. This makes cost of the compensator high.
The compensator has two effects as seen from (3.40), i.e., it alters the no load supply voltage
(E) and it modifies the sensitivity of supply point voltage to the variation in the load reactive power.
Differentiating (3.40) with respect to Ql , we get,
dV
E/Ssc
=−
dQl
1 + Kr E/Ssc
(3.41)
which is voltage sensitivity of supply point voltage to the load reactive power. It can be seen that
the voltage sensitivity is reduced as compared to the voltage sensitivity without compensator as
indicated in (3.38).
It is useful to express the slope (−E/Ssc ) by a term in a form similar to Kγ = dQγ /dV , as given
below.
Ssc
E
E
= −
Ssc
Ks = −
Thus,
1
Ks
Substituting V from (3.39) into (3.35), the following is obtained.
Ql + Qγ
Qγ = Kγ E 1 −
− Vk
Ssc
Collecting the coefficients of Qγ from both sides of the above equation, we get
Kγ
Ql
Qγ =
E 1−
− Vk
1 + Kγ (E/Ssc )
Ssc
(3.42)
(3.43)
(3.44)
Setting knee voltage Vk of the compensator equal to system voltage E i.e., Vk = E, the above
equation is simplified to,
Kγ (E/Ssc )
Ql
1 + Kγ (E/Ssc )
Kγ /Ks
= −
Ql .
1 + Kγ /Ks
Qγ = −
83
(3.45)
From the above equation it is observed that, when compensator gain Kγ → ∞, Qγ → −Ql . This
indicates perfect compensation of the load reactive power in order to regulate the load bus voltage.
Example 3.2 Consider a three-phase system with line-line voltage 11 kV and short circuit capacity
of 480 MVA. With compensator gain of 100 pu determine voltage sensitivity with and without
compensator. For each case, if a load reactive power changes by 10 MVArs, find out the change in
load bus voltage assuming linear relationship between V-Q characteristics. Also find relationship
between compensator and load reactive powers.
Solution: The voltage sensitivity can be computed using the following equation.
dV
E/Ssc
=−
dQl
1 + Kγ E/Ssc
√
Without compensator Kγ = 0, E = (11/ 3) = 6.35 kV and Ssc = 480/3 = 160 MVA.
Substituting these values in the above equation, the voltage sensitivity is given below.
dV
6.35/160
=−
= −0.039
dQl
1 + 0 × 6.35/160
The change in voltage due to variation of reactive power by 10 MVArs, ∆V = −0.039 × 10 =
−0.39 kV.
With compensator, Kγ = 100
dV
6.35/160
=−
= −0.0078
dQl
1 + 100 × 6.35/160
The change in voltage due to variation of reactive power by 10 MVArs, ∆V = −0.0078 × 10 =
−0.078 kV.
Thus it is seen that, with finite compensator gain their is quite reduction in the voltage sensitivity,
which means that the load bus is fairly constant for considerable change in the load reactive power.
The compensator reactive power Qγ and load reactive power Ql are related by equation (3.45) and
is given below.
Kγ (E/Ssc )
100 × (6.35/160)
Ql = −
Ql
1 + Kγ (E/Ssc )
1 + 100 × (6.35/160)
= −0.79 Ql
Qγ = −
It can be observed that when compensator gain, (Qγ ) is quite large, then compensator reactive
power Qγ is equal and opposite to that of load reactive power i.e., Qγ = −Ql . It is further observed
that due to finite compensator gain i.e., Kγ = 100, reactive power is partially compensated The
compensator reactive power varies from 0 to 7.9 MVAr for 0 to 10 MVAr change in the load
reactive power.
3.4
Phase Balancing and Power Factor Correction of Unbalanced Loads
So far we have discussed voltage regulation and power factor correction for single phase systems.
In this section we will focus on balancing of three-phase unbalanced loads. In considering unbalanced loads, both load and compensator are modeled in terms of their admittances and impedances.
84
3.4.1
Three-phase Unbalanced Loads
Consider a three-phase three-wire system suppling unbalanced load as shown in Fig. 3.8.
V
V
an
bn
Ia
I1
Ib
N
V
cn
Za
Zb
n
I2
Ic
Zc
Fig. 3.8 Three-phase unbalanced load
Applying Kirchoff’s voltage law for the two loops shown in the figure, we have the following
equations.
−V an + Za I 1 + Zb (I 1 − I 2 ) + V bn = 0
−V bn + Zb I 2 + Zb (I 2 − I 1 ) + V cn = 0
(3.46)
Rearranging above, we get the following.
V an − V bn = (Za + Zb ) I 1 − Zb I 2
V bn − V cn = (Zb + Zc ) I 2 − Zb I 1
The above can be represented in matrix form as given below.
V an − V bn
I1
(Za + Zb )
−Zb
=
−Zb
(Zb + Zc )
V bn − V cn
I2
Therefore the currents are given as below.
−1 I1
(Za + Zb )
−Zb
V an − V bn
=
−Zb
(Zb + Zc )
I2
V bn − V cn
1
(Zb + Zc )
Zb
V an − V bn
=
Zb
(Za + Zb )
V bn − V cn
∆Z
1
I1
(Zb + Zc )
Zb
V an − V bn
Therefore,
=
.
Zb
(Za + Zb )
I2
V bn − V cn
∆Z
(3.47)
(3.48)
(3.49)
Where, ∆Z = (Zb + Zc )(Za + Zb ) − Zb2 = Za Zb + Zb Zc + Zc Za . The current I 1 is given below.
1 I1 =
(Zb + Zc )(V an − V bn ) + Zb (V bn − V cn )
∆Z
1 =
(Zb + Zc )V an − Zc V bn − Zb V cn
(3.50)
∆Z
85
Similarly,
1
∆Z
1
=
∆Z
I2 =
Zb (V an − V bn ) + (Za + Zb )(V bn − V cn )
Zb V an + Za V bn − (Za + Zb )V cn
(3.51)
Now,
1 (Zb + Zc )V an − Zc V bn − Zb V cn
∆Z
I2 − I1
1 Zb V an + Za V bn − (Za + Zb )V cn − (Zb + Zc )V an + Zc V bn + Zb V cn
∆
Z
(Zc + Za )V bn − Za V cn − Zc Van
∆Z
(Zc + Za )V bn − Zc V an − Za V cn
(3.52)
∆Z
Ia = I1 =
Ib =
=
=
=
and
(Za + Zb )V cn − Zb V an − Za V bn
∆Z
Alternatively phase currents can be expressed as following.
I c = −I 2 = −I b − I a =
V an − V N n
Za
V bn − V N n
=
Zb
V cn − V N n
=
Zc
(3.53)
Ia =
Ib
Ic
(3.54)
Applying Kirchoff’s current law at node N , we get I a + I b + I c = 0. Therefore from the above
equation,
V an − V N n V bn − V N n V cn − V N n
+
+
= 0.
Za
Zb
Zc
(3.55)
Which implies that,
V an V bn V cn
1
1
1
Za Zb + Zb Zc + Zc Za
+
+
=
+
+
V Nn =
V Nn
(3.56)
Za
Zb
Zc
Za Zb Zc
Za Zb Zc
From the above equation the voltage between the load and system neutral can be found. It is given
below.
Za Zb Zc V an V bn V cn
V Nn =
+
+
∆Z
Za
Zb
Zc
1
V an V bn V cn
= 1
+
+
(3.57)
Za
Zb
Zc
+ Z1b + Z1c
Za
86
Some interesting points are observed from the above formulation.
1. If both source voltage and load
impedances are balanced i.e., Za = Zb = Zc = Z, then
1
V N n = 3 V an + V bn + V cn = 0. Thus their will not be any voltage between two neutrals.
2. If supply voltage are balanced and load impedances are unbalanced, then V N n 6=0 and is
given by the above equation.
3. If supply voltages are not balanced but load impedances are identical, then V N n =
This equivalent to zero sequence voltage V 0 .
1
3
V an + V bn + V cn .
It is interesting to note that if the two neutrals are connected together i.e., V N n = 0, then each
phase become independent through neutral. Such configuration is called three-phase four-wire
system. In general, three-phase four-wire system has following properties.
)
V Nn = 0
(3.58)
I a + I b + I c = I N n 6= 0
The current I N n is equivalent to zero sequence current (I 0 ) and it will flow in the neutral wire.
For three-phase three-wire system, the zero sequence current is always zero and therefore following
properties are satisfied.
)
V N n 6= 0
(3.59)
Ia + Ib + Ic = 0
Thus, it is interesting to observe that three-phase three-wire and three-phase four-wire system have
dual properties in regard to neutral voltage and current.
3.4.2
Representation of Three-phase Delta Connected Unbalanced Load
A three-phase delta connected unbalanced and its equivalent star connected load are shown in Fig.
3.9(a) and (b) respectively. The three-phase load is represented by line-line admittances as given
below.
c
c
Ic
Ic
Yl
Z lc
ca
l
bc
Y
Z lb
Ib
Ib
a
b
Yl
Ia
n
a
b
ab
Z la
Ia
(a)
(b)
Fig. 3.9 (a) An unbalanced delta connected load (b) Its equivalent star connected load
87

ab
Ylab = Gab
+
jB
l
l 

bc
Ylbc = Gbc
l + jBl 
ca 
Ylca = Gca
l + jBl
(3.60)
The delta connected load can be equivalently converted to star connected load using following
expressions.

Zlab Zlca


= ab

Zl + Zlbc + Zlca 




bc ab
Zl Zl
b
Zl = ab
Zl + Zlbc + Zlca 



ca bc

Z
Z

l
l
c


Zl = ab
bc
ca
Zl + Zl + Zl
Zla
(3.61)
Where Zlab = 1/Ylab , Zlbc = 1/Ylbc and Zlca = 1/Ylca . The above equation can also be written in
admittance form

Ylab Ylbc + Ylbc Ylca + Ylca Ylab 

Yl =


Ylbc



ab bc
bc ca
ca ab 
Y
Y
+
Y
Y
+
Y
Y
l
l
l
l
Yl b = l l

Ylca


ab bc
bc ca
ca ab 

Y
Y
+
Y
Y
+
Y
Y
l
l
l
l 


Yl c = l l
Ylab
a
(3.62)
Example 3.3 Consider three-phase system supply a delta connected unbalanced load with Zal =
Ra = 10 Ω, Zbl = Rb = 15 Ω and Zcl = Rc = 30 Ω as shown in Fig. 3.8. Determine the voltage
between neutrals and find the phase currents. Assume a balance supply voltage with rms value of
230 V. Find out the vector and arithmetic power factor. Comment upon the results.
88
Solution: The voltage between neutrals V N n is given as following.
VN n =
=
=
=
=
=
VN n =
V an V bn V cn
Ra Rb Rc
+
+
Ra Rb + Rb Rc + Rc Ra Ra
Rb
Rc
o
10 × 15 × 30
V ∠0
V ∠−120o V ∠120o
+
+
10 × 15 + 15 × 30 + 30 × 10
10
15
30
o
o
o
4500 3V ∠0 + 2V ∠−120 + V ∠120
900
30
"
√ !
√ !#
3
3
4500 1
1
1
V 3+2 − −j
+ − +j
900 30
2
2
2
2
"
√
√ #
V
1
3
3
3 − 1 − − j2 ×
+j
6
2
2
2
"
√ #
V 3
3
1
1
−j
=V
− j √ = V [0.25 − j0.1443]
6 2
2
4
4 3
V
√ ∠−30o = 66.39∠−30o Volts
2 3
Knowing this voltage, we can find phase currents as following.
Ia =
=
=
=
√
V an − V N n
V ∠0o − V /(2 3)∠−30o
=
Ra
10
V [1 − 0.25 + j0.1443]
10
230 × [0.075 + j0.01443]
17.56∠10.89o Amps
Similarly,
Ib
√
V bn − V N n
V ∠ − 120o − V /(2 3)∠−30o
=
=
Rb
15
= 230 × [−0.05 − j0.04811]
= 15.94∠−136.1o Amps
and
Ic
√
V ∠120o − V /(2 3)∠−30o
V cn − V N n
=
=
Zc
30
= 230 × [−0.025 + j0.03367]
= 9.64 ∠126.58o Amps
89
It can been seen that I a + I b + I c = 0. The phase powers are computed as below.
S a = V a (I a )∗ = Pa + jQa = 230 × 17.56∠ − 10.81o = 3976.12 − j757.48 VA
S b = V b (I b )∗ = Pb + jQb = 230 × 15.94∠(−120o + 136.1o = 3522.4 + j1016.69 VA
S c = V c (I c )∗ = Pc + jQc = 230 × 9.64∠(120o − 126.58o ) = 2202.59 − j254.06 VA
From the
apparent power S V = S a + S b + S c = 9692.11 + j0 VA. Therefore,
above the total
SV = S a + S b + S c = 9692.11 VA.
The total arithmetic apparent power SA = S a + S b + S c == 9922.2 VA. Therefore, the
arithmetic and vector apparent power factors are given by,
P
9692.11
=
= 0.9768
SA
9922.2
P
9622.11
= 1.00.
=
=
SV
9622.11
p fA =
p fV
It is interesting to note that although the load in each phase is resistive but each phase has some
reactive power. This is due to unbalance of the load currents. This apparently increases the rating
of power conductors for given amount of power transfer. It is also to be noted that the net reactive
power Q = Qa + Qb + Qc = 0 leading to the unity vector apparent power factor . However the
arithmetic apparent power factor is less than unity showing the effect of the unbalance loads on the
power factor.
3.4.3
An Alternate Approach to Determine Phase Currents and Powers
In this section, an alternate approach will be discussed to solve phase currents and powers directly
without computing the neutral voltage for the system shown in Fig.3.9(a). First we express threephase voltage in the following form.
V a = V ∠0o
V b = V ∠ − 120o = α2 V
V c = V ∠1200 = αV
(3.63)
Where, in above equation, α is known as complex operator and value of α and α2 are given below.
√
α = ej2π/3 = 1∠120o = −1/2 + j 3/2
√
α2 = ej4π/3 = 1∠240 = 1∠ − 120 = −1/2 − j 3/2
(3.64)
Also note the following property,
1 + α + α2 = 0.
Using the above, the line to line voltages can be expressed as following.
90
(3.65)
V ab = V a − V b = (1 − α2 )V
V bc = V b − V c = (α2 − α)V
V ca = V c − V a = (α − 1)V
(3.66)
Therefore, currents in line ab, bc and ca are given as,
ab
2
I abl = Y ab
l V ab = Yl (1 − α )V
I bcl = Ylbc V bc = Ylbc (α2 − α)V
I cal = Ylca V ca = Ylca (α − 1)V
(3.67)
Hence line currents are given as,
I al = I abl − I cal = [Ylab (1 − α2 ) − Ylca (α − 1)]V
I bl = I bcl − I abl = [Ylbc (α2 − α) − Ylab (1 − α2 )]V
I cl = I cal − I bcl = [Ylca (α − 1) − Ylbc (α2 − α)]V
(3.68)
Example 3.4 Compute line currents by using above expressions directly for the problem in Example 3.3.
Solution: To compute line currents directly from the above expressions, we need to compute Ylab .
These are given below
1
Zlc
=
Zlab
Zla Zlb + Zlb Zlc + Zlc Zla
Zla
1
=
=
Zlbc
Zla Zlb + Zlb Zlc + Zlc Zla
1
Zlb
=
=
Zlca
Zla Zlb + Zlb Zlc + Zlc Zla
Ylab =
Ylbc
Ylca
(3.69)
Substituting, Zal = Ra = 10 Ω, Zbl = Rb = 15 Ω and Zcl = Rc = 30 Ω into above equation, we get
the following.
1
Ω
30
1
Ylbc = Gbc = Ω
90
1
Ylca = Gca = Ω
60
Ylab = Gab =
Substituting above values of the admittances in (3.68) , line currents are computed as below.
91
"
Ia =
1
30
(
)#
√ )
√
1
3
1
1
3
1 − (− − j
) −
(− + j
)−1
V
2
2
60
2
2
(
= V (0.075 + j0.0144)
= 0.07637 V ∠10.89o
= 17.56∠10.89o Amps, for V=230 V
Similarly for Phase-b current,
" (
(
√
√ )
√ )#
1
1
3
1
3
1
1
3
Ib =
(− − j
) − (− + j
) −
1 − (− − j
)
V
90
2
2
2
2
30
2
2
= V (−0.05 − j0.0481)
= 0.06933 V ∠ − 136.1o
= 15.94∠ − 136.91o Amps, for V=230 V
Similarly for Phase-c current,
"
Ic =
1
60
)
(
√
√
√ )#
1
3
1
1
3
1
3
(− + j
) − 1) −
(− − j
) − (− + j
)
V
2
2
90
2
2
2
2
(
= V (−0.025 + j0.0336)
= 0.04194 V ∠126.58o
= 9.64∠126.58o Amps, for V=230 V
Thus it is found that the above values are similar to what have been found in previous Example
3.3. The other quantities such as powers and power factors are same.
3.4.4
An Example of Balancing an Unbalanced Delta Connected Load
An unbalanced delta connected load is shown in Fig. 3.10(a). As can be seen from the figure that
between phase-a and b there is admittance Ylab = Gab
l and other two branches are open. This is
an example of extreme unbalanced load. Obviously for this load, line currents will be extremely
unbalanced. Now we aim to make these line currents to be balanced and in phase with their phase
voltages. So, let us assume that we add admittances Yγab , Yγbc and Yγca between phases ab, bc and
ca respectively as shown in Fig. 3.10(b) and (c). Let values of compensator susceptances are given
by,
Yγab = 0
√
Yγbc = jGab
l / 3
√
Yγca = −jGab
l / 3
92
3
/
j
G ab
l
j
G ab
l /
3
Y
/
Yl bc
0
3
Y bc
ab
jG l
/
0
0
Yl bc
0

ab
jGl
ca
Yl
ca
Yl

ca
Y
Ic
ca
Ic
Y
Ic
c
c
bc
c
3
Ib
b
Ia
Yl  G
ab
ab
l
a
Ib
a
b
Yl ab  Glab
Yab  0
Ia
(a)
Ib
b
Y ab  Glab
Ia
(b)
(c)
Fig. 3.10 (a) An unbalanced three-phase load (b) With compensator (c) Compensated system
Thus total admittances between lines are given by,
ab
Y ab = Ylab + Yγab = Gab
l + 0 = Gl
√
√
ab
Y bc = Ylbc + Yγbc = 0 + jGab
l / 3 = jGl / 3
√
√
ab
Y ca = Ylca + Yγca = 0 − jGab
l / 3 = −jGl / 3.
Therefore the impedances between load lines are given by,
1
1
=
Y ab
Gab
l
√
−j 3
1
=
=
Y bc
Gab
√l
1
j 3
=
= ab
ca
Y
Gl
Z ab =
Z bc
Z ca
√
√
ab
ab
ab
Note that Z ab + Z bc + Z ca = 1/Gab
l − j 3/Gl + j 3/Gl = 1/Gl .
The impedances, Za , Zb and Zc of equivalent star connected load are given as follows.
Z ab × Z ca
Z ab + Z bc√+ Z ca
1
j 3
1
= ( ab × ab )/( ab )
Gl
Gl
Gl
√
j 3
=
Gab
l
Za =
93
a
Z bc × Z ab
ca
Z ab + Z bc +
√Z
−j 3
1
1
)/( ab )
= ( ab ×
ab
Gl
Gl
Gl
√
−j 3
=
Gab
l
Zb =
Z ca × Z bc
Z ab √
+ Z bc +√Z ca
1
−j 3 j 3
= ( ab × ab )/( ab )
Gl
Gl
Gl
3
=
Gab
l
Zc =
The above impedances seen from the load side are shown in Fig. 3.11(a) below. Using (3.57),
c
Ic
Ic
3
Z  ab
Gl
Load
Zlb   j
c
1
Glab
c
l
3
Glab
Ib
b
Zla  j
1
Glab
Source
n
3
Glab
Ib
a
b
Ia
N
1
Glab
a
Ia
Fig. 3.11 Compensated system (a) Load side (b) Source side
the voltage between load and system neutral of delta equivalent star load as shown in Fig. 3.11, is
computed as below.
1
V an V bn V cn
VN n = 1
+
+
Za
Zb
Zc
+ Z1b + Z1c
Za
1
V ∠0o
V ∠ − 120o V ∠120o
√
√
+
+
=
1
3
√ 1
3/Gab
+ (−j √3/G
j 3/Gab
−j 3/Gab
ab ) + Gab
l
l
l
(j 3/Gab
)
l
l
l
ab
ab
3V
Gl
G
=
− j √l
ab
3
Gl
3
√ !
1
3
−j
= 2V
2
2
= 2 V ∠ − 60o
94
Using above value of neutral voltage the line currents are computed as following.
Ia =
=
V an − V N n
Za
[V ∠0o − 2 V ∠ − 60o ]
√
j Gab3
l
=
Ib =
=
Gab
l
Gab
l
V =
Va
V bn − V N n
Zb
[V ∠ − 120o − 2 V ∠ − 60o ]
√
−j Gab3
l
=
=
Ic =
=
Gab
l
Gab
l
o
V ∠240
Vb
V cn − V N n
Zc
[V ∠120o − 2 V ∠ − 60o ]
3
Gab
l
o
= Gab
l V ∠120
= Gab
l Vc
From the above example, it is seen that the currents in each phase are balanced and in phase with
their respective voltages. This is equivalently shown in Fig. 3.11(b). It is to be mentioned here that
the two neutrals in Fig. 3.11 are not same. In Fig. 3.11(b), the neutral N is same as the system
neutral as shown in Fig. 3.8, whereas in Fig. 3.11(a),
V N n = 2 V ∠−60o .√However the reader
√
ca
may be curious to know why Yγab = 0, Yγbc = jGab
= −jGab
l / 3 and γ
l / 3 have been chosen
as compensator admittance values. The answer of the question can be found by going following
sections.
3.5
A Generalized Approach for Load Compensation using Symmetrical
Components
In the previous section, we have expressed line currents I a , I b and I c , in terms load admittances
and the voltage V for a delta connected unbalanced load as shown in Fig 3.12(a). For the sake of
completeness, theses are reproduced below.
95
I al = I abl − I cal = [Ylab (1 − α2 ) − Ylca (α − 1)]V
I bl = I bcl − I abl = [Ylbc (α2 − α) − Ylab (1 − α2 )]V
I cl = I cal − I bcl = [Ylca (α − 1) − Ylbc (α2 − α)]V
c
c
Ic
I cl
Yl
Y
Yl ab
b
ca
ca 
l
Ybc bc
Yl
ca
l
bc
I bl
I al
(3.70)
Ib
a
b
Ia
(a)
Y
Y
Yl ab
a
Yab
(b)
Fig. 3.12 (a) An unbalanced delta connested load (b) Compensated system
Since loads currents are unbalanced, these will have positive and negative currents. The zero
sequence current will be zero as it is three-phase and three-wire system. These symmetrical components of the load currents are expressed as following.
 
 

I 0l
I al
1 1 1
I 1l  = √1 1 a a2   I bl 
(3.71)
2
3
1
a
a
I 2l
I cl
√
In equation (3.71), a factor of 1/ 3 is considered to have unitary symmetrical transformation.
From the above equation, zero sequence current is given below.
√
I 0l = I al + I al + I al / 3
The positive sequence current is as follows.
1 I 1l = √ I al + αI bl + α2 I cl
3
1
= √ [ Ylab (1 − α2 ) − Ylca (α − 1) + α Ylbc (α2 − α) − Ylab (1 − α2 )
3
+α2 Ylca (α − 1) − Ylbc (α − α2 ) ] V
1
= √ [ Ylab − α2 Ylab + Ylca − αYlca + α3 Ylbc − α2 Ylbc − αYlab − α3 Ylab + α3 Ylca − α2 Ylca
3
−α4 Ylbc + α3 Ylbc ] V
√
= Ylab + Ylbc + Ylca V 3
96
Similarly negative sequence component of the current is,
1 I 2l = √
I al + α2 I bl + αI cl
3
1
= √ [Ylab (1 − α2 ) − Ylca (α − 1) + α2 Ylbc (α2 − α) − Ylab (1 − α2 )
3
+α Ylca (α − 1) − Ylbc (α2 − α) ]V̄
1
= √ [ Ylab − α2 Ylab − αYlca + Ylca + α4 Ylbc − α3 Ylbc − α2 Ylab
3
+α4 Ylab + α2 Ylca − αYlca − α3 Ylbc + α2 Ylbc ] V
1
= √ [ −3α2 Ylab − 3Ylbc − 3αYlca ] V
3
√
= −[α2 Ylab + Ylbc + αYlca ] 3V
From the above, it can be written that,
I 0l = 0
√
I 1l = Ylab + Ylbc + Ylca 3V
I 2l = − α2 Ylab + Ylbc + αYl
√
ca
(3.72)
3V
When compensator is used, three delta branches Yγab , Yγbc and Yγca are added as shown in Fig.
3.12(b). Using above analysis, the sequence components of the compensator currents can be given
as below.
I 0γ = 0
√
3V
√
= − α2 Yγab + Yγbc + αYγca
3V
I 1γ =
I 2γ
Yγab + Yγbc + Yγca
(3.73)
bc
ca
Since, compensator currents are purely reactive, i.e., Gab
γ = Gγ = Gγ = 0,
ab
ab
Yγab = Gab
γ + jBγ = jBγ
bc
bc
Yγbc = Gbc
γ + jBγ = jBγ
ca
ca
Yγca = Gca
γ + jBγ = jBγ .
(3.74)
Using above, the compensated sequence currents can be written as,
I 0γ = 0
I 1γ = j Bγab + Bγbc + Bγca
I 2γ
√
3V
√
= −j(α2 Bγab + Bγbc + αBγca ) 3 V
(3.75)
Knowing nature of compensator and load currents, we can set compensation objectives as following.
1. All negative sequence component of the load current must be supplied from the compensator
negative current, i.e.,
I 2l = −I 2γ
97
(3.76)
The above further implies that,
Re I 2l + j Im I 2l = −Re I 2γ − j Im I 2γ
(3.77)
2. The total positive sequence current, which is source current should have desired power factor
from the source, i.e.,
Im (I 1l + I 1γ )
= tan φ = β
Re (I 1l + I 1γ )
(3.78)
Where, φ is the desired phase angle between the line currents and the supply voltages. The above
equation thus implies that,
Im (I 1l + I 1γ ) = β Re (I 1l + I 1γ )
(3.79)
Since Re (I 1γ ) = 0, the above equation is rewritten as following.
Im (I 1l ) − β Re (I 1l ) = −Im (I 1γ )
(3.80)
The equation (3.77) gives two conditions and equation (3.79) gives one condition. There are
three unknown variables, i.e., Bγab , Bγbc and Bγca and three conditions. Therefore the unknown
variables can be solved. This is described in the following section. Using (3.75), the current I 2γ is
expressed as following.
√
I 2γ = −j[α2 Bγab + Bγbc + αBγca ] 3 V
"
#
√ !
√ !
√
1
1
3
3
= −j
− −j
Bγab + Bγbc + − + j
Bγca
3V
2
2
2
2
"
!
√
√
#
√
3 ab
3 ca
1 ab
1
=
−
Bγ +
Bγ − j − Bγ + Bγbc − Bγca
3V
2
2
2
2
= Re I 2γ − j Im I 2γ
Thus the above equation implies that
!
√
√
1
3 ab
3 ca
1
Bγ −
Bγ = − √ Re I 2γ = √ Re I 2l
2
2
3V
3V
(3.81)
(3.82)
and,
1
1
− Bγab + Bγbc − Bγca
2
2
1
1
= − √ Im I 2γ = √ Im I 2l
3V
3V
(3.83)
Or
1
−Bγab + 2 Bγbc − Bγca = √ 2 Im I 2l
3V
98
(3.84)
From (3.75), Im (I 1γ ) can be written as,
Im (I 1γ ) = Bγab + Bγbc + Bγca
√
3 V.
(3.85)
Substituting Im (I 1γ ) from above equation into (3.85), we get the following.
1
1 Im (I 1l ) − β Re (I 1l )
−(Bγab + Bγbc + Bγca ) = − √ Im (I 1γ ) = √
3V
3V
(3.86)
Subtracting (3.86) from (??), the following is obtained,
Bγbc =
−1
√ [Im (I 1l ) − 2 Im (I 2l ) − β Re (I 1l )].
3 3V̄
(3.87)
Now, from (3.82) we have
1
1
1
− Bγab − Bγca = √ Im (I 2l ) − Bγbc
2
2
3V
−1 1
= √ Im (I 2l ) − √
Im (I 1l ) − β Re (I 1l ) − 2 Im (I 2l )
3V
3 3V
1 = √
(3.88)
Im (I 2l ) + Im (I 1l ) − β Re (I 1l )
3 3V
Reconsidering (3.88) and (3.83), we have
1
− Bγab −
2
1 ab
B −
2 γ
1 ca
1 √
Bγ =
Im (I 1l ) + Im (I 2l ) − β Re (I 1l )
2
3 3V
√
1 ca
1
√ [ 3Re (I 2l )]
Bγ =
2
3 3V
Adding above equations, we get
Bγca =
√
−1
√ [Im (I 1l ) + Im (I 2l ) + 3 Re (I 2l ) − β Re (I 1l )].
3 3V
(3.89)
Therefore,
2 √
Bγab = Bγca + √ [ 3 Re (I 2l )]
3 3V
√
√
−1
√ [Im (I 1l ) + Im (I 2l ) + 3 Re (I 2l ) − β Re (I 1l ) − 2 3 Re (I 2l )]
=
3 3V
√
−1
= √ [Im (I 1l ) + Im (I 2l ) − 3 Re (I 2l ) − β Re (I 1l )]
(3.90)
3 3V
Similarly, Bγbc can be written as in the following.
1 Bγbc = − √
Im(I 1l ) − 2Im(I 2l ) − β Re(I 1l )
3 3V
(3.91)
(3.92)
99
From the above, the compensator susceptances in terms of real and imaginary parts of the load
current can be written as following.
√
−1
√ [Im (I 1l ) + Im (I 2l ) − 3 Re (I 2l ) − β Re (I 1l )]
3 3V
1
= − √ [Im(I 1l ) − 2Im(I 2l ) − β Re(I 1l )]
3 3V
√
−1
= √ [Im (I 1l ) + Im (I 2l ) + 3 Re (I 2l ) − β Re (I 1l )]
3 3V
Bγab =
Bγbc
Bγca
(3.93)
In the above equation, the susceptances of the compensator are expressed in terms of real and
imaginary parts of symmetrical components of load currents. It is however advantageous to express
these susceptances in terms of instantaneous values of voltages and currents from implementation
point of view. The first step to achieve this is to express these susceptances in terms of load
currents, i.e., I al , I bl and I cl , which is described below. Using equation (3.71), the sequence
components of the load currents are expressed as,
1 I¯0l = √ I¯al + I¯bl + I¯cl
3
1
I¯1l = √ I¯al + αI¯bl + α2 I¯cl
3
1
I¯2l = √ I¯al + α2 I¯1l + αI¯cl .
3
(3.94)
Substituting these values of sequence components of load currents, in (3.93), we can obtain compensator susceptances in terms of real and inaginary components of the load currents. Let us start
from the Bγbc , as obtained following.
1 Bγbc = − √
Im(I 1l ) − 2Im(I 2l ) − β Re(I 1l )
3 3V
1
I al + αI bl + α2 I cl
I al + α2 I bl + αI cl
I al + αI bl + α2 I cl
√
√
√
=− √
Im
− 2 Im
− β Re
3 3V
3
3
3
1 =−
Im (−I al + (2 + 3α)I bl + (2 + 3α2 )I cl − β Re (I al + αI bl + α2 I cl )
9V
1 Im −I al + 2I bl + 2I cl + 3αI bl + 3α2 I cl − β Re (I al + αI bl + α2 I cl )
=−
9V
By adding and subracting I bl and I cl in the above equation we get,
Bγbc = −
1 Im (−I al − I bl − I cl ) + 3I bl + 3I cl + 3α I bl + α2 I cl − β Re(I al + αI bl + α2 I cl )
9V
We know that I al +I bl +I cl =0, therefore I al + I bl = −I cl .
Bγbc
1
=−
3V
2
−Im I al + Im αI bl + Im α I cl
100
β
2
− Re I al + αI bl + α I cl
(3.95)
3
Similarly, it can be proved that,
Bγca
1
=−
3V
β
2
2
Im I al − Im αI bl + Im α I cl − Re I al + αI bl + α I cl
3
Bγab
1
=−
3V
2
Im I al + Im αI bl − Im α I cl
β
− Re I al + αI bl + α2 I cl
3
(3.96)
(3.97)
The above expressions for Bγca and Bγab are proved below. For convenience, the last term associated
with β is not considered. For the sake simplicity in equations (3.96) and (3.97) are proved to those
given in equations (3.93).
−1 Im I al − Im αI bl + Im α2 I cl
3V " (
)#
2
I 0l + I 1l + I 2l
I 0l + α2 I 1l + αI 2l
I
+
αI
+
α
I
1
0l
1l
2l
√
√
√
=−
Im
−α
+ α2
3V
3
3
3
Bγca =
Since I 0l =0
1
Bγca = − √
3 3V
1
=− √
3 3V
1
=− √
3 3V
1
=− √
3 3V
Im I 1l − 2α2 I 2l
"
√ ! #
3
1
Im I 1l − 2 − − j
I 2l
2
2
i
h
√
Im I 1l + I 2l + j 3I 2l
h
√
i
Im I 1l + Im I 2l + 3Re I 2l
Note that Im(jI 2l ) = Re(I 2l ). Adding β term, we get the following.
i
√
1 h
Bγca = − √
Im(I 1l ) + Im(I 2l ) + 3Re I 2l − βRe(I 1l )
3 3V
Similarly,
1 Im I al + Im αI bl − Im α2 I cl
3V " (
)#
2
I 0l + I 1l + I 2l
I 0l + α2 I 1l + αI 2l
1
2 I 0l + αI 1l + α I 2l
√
√
√
=−
Im
+α
−α
3V
3
3
3
Bγab = −
101
1
Bγab = − √ Im I 1l − 2αI 2l
3 3V
"
√ ! #
3
1
1
= − √ Im I 1l − 2 − + j
I 2l
2
2
3 3V
i
h
√
1
√
=−
Im I 1l + I 2l − j 3I 2l
3 3V
√
i
1 h
=− √
Im I 1l + Im I 2l − 3Re I 2l
3 3V
Thus, Compensator susceptances are expressed as following.
1
β
2
2
Im(I al ) + Im(αI bl ) − Im(α I cl ) − Re(I al + αI bl + α I cl )
=−
3V
3
1
β
bc
2
2
Bγ = −
−Im(I al ) + Im(αI bl ) + Im(α I cl ) − Re(I al + αI bl + α I cl )
(3.98)
3V
3
1
β
Bγca = −
Im(I al ) − Im(αI bl ) + Im(α2 I cl ) − Re(I al + αI bl + α2 I cl )
3V
3
An unity power factor is desired from the source. For this cos φl = 1, implying tan φl = 0 hence
β = 0. Thus we have,
1 Bγab = −
Im I al + Im αI bl − Im α2 I cl
3V
1 −Im I al + Im αI bl + Im α2 I cl
(3.99)
Bγbc = −
3V
1 Bγca = −
Im I al − Im αI bl + Im α2 I cl
3V
The above equations are easy to realize in order to find compensator susceptances. As mentioned
above, sampling and averaging techniques will be used to convert above equation into their time
equivalents. These are described below.
Bγab
3.5.1
Sampling Method
Each current phasor in above equation can be expressed as,
I al = Re(I al ) + jIm(I al )
= Ial,R + jIal,X
An instantaneous phase current is written as follows.
√
ial (t) = 2 Im (I al ejωt )
√
= 2 Im (Ial,R + jIal,X ) ejωt
√
= 2 Im [(Ial,R + jIal,X )(cos ωt + j sin ωt)]
√
= 2 Im [(Ial,R cos ωt − Ial,X sin ωt) + j(Ial,R sin ωt + Ial,X cos ωt)]
√
= 2 [(Ial,R sin ωt + Ial,X cos ωt)]
102
(3.100)
(3.101)
ial (t)
Im (I al ) = I al,X = √
2
at sin ωt = 0, cos ωt = 1
(3.102)
From equation (3.63), the phase voltages can be expressed as below.
√
va (t) = 2 V sin ωt
√
vb (t) = 2 V sin(ωt − 120o )
√
vc (t) = 2 V sin(ωt + 120o )
(3.103)
From above voltage expressions, it is to be noted that, sin ωt = 0, cos ωt = 1 implies that the
phase-a voltage, va (t) is going through a positive zero crossing, hence, va (t) = 0 and dtd va (t) = 0.
Therefore, equation (3.102), can be expressed as following.
ial (t)
I a,l = √ when, va (t) = 0, dva /dt > 0
2
(3.104)
I b,l = Ibl,R + jIbl,X
(3.105)
Similarly,
Therefore,
α (I b,l ) = α(Ibl,R + jIbl,X )
√ !
1
3
= − +j
(Ibl,R + jIbl,X )
2
2
!
!
√
√
1
3
3
1
= − Ibl,R −
Ibl,X + j
Ibl,R − Ibl,X
2
2
2
2
(3.106)
From the above,
√
Im {α (Ibl )} =
3
1
Ibl,R − Ibl,X
2
2
103
(3.107)
Similar to equation, (3.101), we can express phase-b current in terms Im (α I bl ), as given below.
√
ibl (t) = 2 Im (I bl ejωt )
√
= 2 Im (α I bl ejwt α−1 )
√
0
= 2 Im (αI bl ej(wt−120 ) )
"
#
√ !
√
1
3
0
(I bl,R + jI bl,X ) ej(wt−120 )
= 2 Im
− +j
2
2
!
!
√
√
√
1
3
3
1
= 2 Im [ − Ibl,R −
Ibl,X + j
Ibl,R − Ibl,X
2
2
2
2
(cos(wt − 1200 ) + j sin(wt − 1200 )) ]
(3.108)
"
#
√
√
√
1
3
3
1
= 2 (− I bl,R −
I bl,X ) sin(wt − 1200 ) + (
I bl,R − I bl,X ) cos(wt − 1200 )
2
2
2
2
From the above equation, we get the following.
ibl (t)
Im (αI bl ) = √
2
when, vb (t) = 0, dvb /dt > 0
(3.109)
when, vc (t) = 0, dvc /dt > 0
(3.110)
Similarly for phase-c, it can proved that,
icl (t)
Im (α2 I cl ) = √
2
Substituting Im (I al ) , Im (αI bl ) and Im (α2 I cl ) from (3.104), (3.109) and (3.110) respectively, in
(3.99), we get the following.
1
Brab = − √
3 2V
1
Brbc = − √
3 2V
1
Brca = − √
3 2V
h
ia |(va =0, dva >0) + ib |(v
dt
h
dvb
b =0, dt >0)
− ic |(vc =0, dvc >0)
i
dt
−ia |(va =0, dva >0) + ib |(v
+ ic |(vc =0, dvc >0)
dt
dt
h
i
ia |(va =0, dva >0) − ib |(v =0, dvb >0) + ic |(vc =0, dvc >0)
dvb
b =0, dt >0)
b
dt
dt
i
(3.111)
dt
Thus the desired compensating susceptances are expressed in terms of the three line currents sampled at instants defined by positive-going zero crossings of the line-neutral voltages va , vb , vc . An
artificial neutral at ground potential may be created measuring voltages va , vb and vc to implement
above algorithm.
3.5.2
Averaging Method
In this method, we express the compensator susceptances in terms of real and reactive power terms
and finally expressed them in time domain through averaging process. The method is described
104
below.
From equation (3.99), susceptance, Bγab , can be re-written as following.
1 Im I al + Im αI bl − Im α2 I cl
3V
1 = − 2 V Im I al + V Im αI bl − V Im α2 I cl
3V
1 = − 2 Im V I al + Im V αI bl − Im V α2 I cl
3V
Bγab = −
(3.112)
Note the following property of phasors and applying it for the simplification of the above expression.
∗
Im V I = −Im V I
∗
(3.113)
Using above equation (3.112) can be written as,
1
3V 2
1
=
3V 2
1
=
3V 2
Bγab =
Im (V I al )∗ + Im (αV a I bl )∗ − Im (α2 V I cl )∗
i
h
∗ ∗
∗ ∗ ∗
2 ∗ ∗ ∗
Im (V a I al ) + Im (α V a I bl ) − Im ((α ) V a I cl )
h
i
∗ ∗
∗ ∗
∗ ∗
Im (V a I al ) + Im (α2 V a I bl ) − Im (αV a I cl )
∗
∗
∗
Since V a = V ∠0o is a reference phasor, therefore V a = V a = V , α2 V a = V b and α V a = V c .
Using this, the above equation can be written as following.
1
=
3V 2
1
Similarly, Bγbc =
3V 2
1
Bγca =
3V 2
Bγab
h
i
∗
∗
∗
Im (V a I al ) + Im (V b I bl ) − Im (V c I cl )
h
i
∗
∗
∗
−Im (V a I al ) + Im (V b I bl ) + Im (V c I cl )
h
i
∗
∗
∗
Im (V a I al ) − Im (V b I bl ) + Im (V c I cl )
(3.114)
It can be further proved that,
Z
1 T
Im (V
=
va (t)∠(−π/2) ial (t) dt
T 0
Z
1 T
∗
Im (V b I b ) =
vb (t)∠(−π/2) ibl (t) dt
T 0
Z
1 T
∗
Im (V c I c ) =
vc (t)∠(−π/2) icl (t) dt
T 0
∗
a I a)
105
(3.115)
In (3.115), the term va (t)∠(−π/2) denotes the voltage va (t) shifted by −π/2 radian in time domain. For balanced voltages, the following relationship between phase and line voltages are true.
√
va (t)∠(−π/2) = vbc (t)/ 3
√
(3.116)
vb (t)∠(−π/2) = vca (t)/ 3
√
vc (t)∠(−π/2) = vca (t)/ 3
From (3.115) and (3.116), the following can be written.
Z T
1
∗
Im (V a I a ) = √
vbc (t) ial (t) dt
3T 0
Z T
1
∗
Im (V b I b ) = √
vca (t) ibl (t) dt
3T 0
Z T
1
∗
Im (V c I c ) = √
vab (t) icl (t) dt
3T 0
∗
∗
(3.117)
∗
Substituting above values of Im (V a I a ), Im (V b I b ) and Im (V c I c ) into (3.114), we get the following.
Bγab
Bγbc
Bγca
Z
1 T
1
√
(vbc ial + vca ibl − vab icl ) dt
=
(3 3V 2 ) T 0
Z
1
1 T
√
=
(−vbc ial + vca ibl + vab icl ) dt
(3 3V 2 ) T 0
Z
1 T
1
√
(vbc ial − vca ibl + vab icl ) dt
=
(3 3V 2 ) T 0
(3.118)
The above equations can directly be used to know the the compensator susceptances by performing
the
R T averaging
R t1 +T on line the product of the line to line voltages and phase load currents. The term
= t1
can be implemented using moving average of one cycle. This improves transient
0
response by computing average value at each instant. But in this case the controller response
which changes the susceptance value, should match to that of the above computing algorithm.
3.6
Compensator Admittance Represented as Positive and Negative Sequence
Admittance Network
Recalling the following relations from equation (3.93) for unity power factor operation i.e. β = 0,
we get the following.
√
−1
Bγab = √ [Im (I 1l ) + Im (I 2l ) − 3 Re (I 2l )]
3 3V
−1
Bγbc = √ [Im (I 1l ) − β Re (I 1l ) − 2Im (I 2l )]
(3.119)
3 3V
√
−1
Bγca = √ [Im (I 1l ) + Im (I 2l ) + 3 Re (I 2l )]
3 3V
106
From these equations, it is evident the the first terms form the positive sequence suceptance as they
involve I 1l terms. Similarly, the second and third terms in above equation form negative sequence
susceptance of the compensator, as these involve I 2l terms. Thus, we can write,
ab
ab
Bγab = Bγ1
+ Bγ2
ab
ab
+ Bγ2
Bγab = Bγ1
Bγab
ab
Bγ1
=
+
(3.120)
ab
Bγ2
Therefore,
1 ab
bc
ca
Bγ1
= Bγ1
= Bγ1
=− √
Im(I¯1l )
3 3V
(3.121)
And,
ab
Bγ2
bc
Bγ2
ca
Bγ2
√
1 = − √
Im(I 2l ) − 3Re(I 2l )
3 3V
1
= − √
−2 Im(I 2l )
3 3V
√
1 = − √
Im(I 2l ) + 3Re(I 2l )
3 3V
(3.122)
Earlier in equation, (3.123), it was established that,
I 0l = 0
√
I 1l = Ylab + Ylbc + Ylca 3V
I 2l = − α2 Ylab + Ylbc + αYlca
√
3V
Noting that,
ab
Ylab = Gab
l + jBl
bc
Ylbc = Gbc
l + jBl
ca
Ylca = Gca
l + jBl
Therefore,
√
Im (I 1l ) = Im ((Ylab + Ylbc + Ylca ) 3V )
√
= (Blab + Blbc + Blca ) 3V
(3.123)
Thus equation (3.121) is re-written as following.
ab
bc
ca
Bγ1
= Bγ1
= Bγ1
=−
1
Blab + Blab + Blca
3
107
(3.124)
ca
bc
ab
using equations (3.122) as following. Knowing that,
and Bγ2
, Bγ2
Now we shall compute Bγ2
√
I¯2l = − α2 Ylab + Ylbc + αYlca
3V
#
"
√ !
√ !
√
3
−1
j
−1 j 3
ab
bc
bc
ca
ca
−
Gab
+
jB
+
G
+
jB
+
+
(G
+
jB
)
3V
=−
l
l
l
l
l
l
2
2
2
2
"
!#
√
√
√
√
√
Gab
3 ab
Gca
3 ca
3 ab Blab
3 ca Blca
l
l
bc
bc
=− −
+
Bl + Gl −
−
Bl − j
Gl +
− Bl −
Gl +
3V
2
2
2
2
2
2
2
2
!#
"
√
√
√
√
ca
ab
ca
√
3
G
3
3
B
3
B
Gab
l
l
l
l
−
Blab − Gbc
+
Blca + j
Gab
− Blbc −
Gca
3V
=
l +
l +
l +
2
2
2
2
2
2
2
2
(3.125)
The above implies that,
Im (I 2l ) =
√
− 3 Re(I 2l ) =
!
√
√
ca
√
3 ab Blab
3
B
l
Gl +
− Blbc −
Gca
3V
l +
2
2
2
2
!
√
√
3 ab 3 ab √ bc
3 ca 3 ca √
G + Bl + 3Gl −
G − Bl
−
3V
2 l
2
2 l
2
ab
Thus, Bγ2
can be given as,
√
√ ca i √
1 h ab
ab
2Bl − Blbc − Blca + 3 Gbc
Bγ2
=− √
−
3 Gl
3V
l
3 3V
√
i
1h
ca
= − 2Blab − Blbc − Blca + 3 Gbc
−
G
l
l
3
1
1
bc
= √ Gca
Blbc + Blca − 2Blab
+
l − Gl
3
3
(3.126)
Similarly,
i
√
1 h
ca
Im(I¯2l ) + 3 Re(I¯2l )
Bγ2
=− √
3 3V "
#
√
√
√
√
ab
ca
√
1
3 ab Bl
3 ca Bl
3 ab 3 ab
3 ca 3 ca √
=− √
Gl +
− Blbc −
Gl +
+
Gl − Bl − 3Gbc
G + Bl
3V
l +
2
2
2
2
2
2
2 l
2
3 3V
i
1 h√ ab √ bc
=−
3Gl − 3Gl − Blab − Blbc + 2Blca
3
1
1
ab
(3.127)
= √ Gbc
+
Blab + Blbc − 2Blca
l − Gl
3
3
bc
And, Bγ2
is computed as below.
108
1 bc
=− √
−2Im(I¯2l )
Bγ2
3 3V
!
√
√
ca
√
2
3 ab Blab
3
B
l
= √
Gl +
− Blbc −
Gca
V 3
l +
2
2
2
2
3 3V
1
1
ca
+
Blab + Blca − 2Blbc
= √ Gab
l − Gl
3
3
(3.128)
Using (3.121), (3.126)-(3.128), We therefore can find the overall compensator susceptances as
following.
ab
ab
Bγab = Bγ1
+ Bγ2
1
1
1
bc
= − Bγab + Bγbc + Bγca + √ Gca
+
Blca + Blbc − 2Blab
l − Gl
3
3
3
1
bc
= −Blab + √ Gca
l − Gl
3
Similarly,
bc
bc
Bγbc = Bγ1
+ Bγ2
1
1
1
ca
ab
ca
bc
−
G
B
+
B
−
2B
+
= − Bγab + Bγbc + Bγca + √ Gab
l
l
l
l
3
3 l
3
1
ca
= −Blbc + √ Gab
l − Gl
3
And,
ca
ca
Bγca = Bγ1
+ Bγ2
1
1
1
ab
Blbc + Blab − 2Blca
= − Bγab + Bγbc + Bγca + √ Gbc
+
l − Gl
3
3
3
1
ab
= −Blca + √ Gbc
l − Gl
3
Thus, the compensator susceptances in terms of load parameters are given as in the following.
1
bc
Bγab = −Blab + √ Gca
l − Gl
3
1
ca
Bγbc = −Blbc + √ Gab
l − Gl
3
1
ca
ca
ab
Bγ = −Bl + √ Gbc
l − Gl
3
109
(3.129)
It is interesting to observe above equations. The first parts of the equation nullifies the effect of the
load susceptances and the second parts of the equations correspond to the unbalance in resistive
load. The two terms together make source current balanced and in phase with the supply voltages.
The compensator’s positive and negative sequence networks are shown in Fig. 3.13 .
What happens if we just use the following values of the compensator susceptances as given below?
Bγab = −Blab
Bγbc = −Blbc
Bγca = −Blca
(3.130)
In above case, load suceptance parts of the admittance are fully compensated. However the source
currents after compensation remain unbalanced due to unbalance conductance parts of the load.
isa
ila
ilb
Source
isb
ilc
isc
I  1,abc
Load
I  2,abc
Bab2
Bab1
Bbc1
Bca1
Bbc2
Bca2
Bab , Bbc , Bca
Fig. 3.13 Sequence networks of the compensator
Example 3.5 For a delta connected load shown in 3.14 , the load admittances are given as following,
ab
Ylab = Gab
l + jBl
bc
Ylbc = Gbc
l + jBl
ca
Ylca = Gca
l + jBl
Given the load parameters:
Zlab = 1/Ylab = 5 + j12 Ω
Zlbc = 1/Ylbc = 3 + j4 Ω
Zlca = 1/Ylca = 9 − j12 Ω
Determine compensator susceptances (Bγab , Bγbc , Bγca ) so that the supply sees the load as balanced
and unity power factor. Also find the line currents and source active and reactive powers before
and after compensation.
110
va
a
ia
ab
ca
N
B
B
vc
ca
ic
Y
Y
ab
vb
ib
c
Y
bc
b
bc
B
Fig. 3.14 A delta connected load
Solution:
Zlab = 5 + j12 Ω ⇒ Ylab = 0.03 − j0.0710 f
Zlbc = 3 + j4 Ω ⇒ Ylbc = 0.12 − j0.16 f
Zlca = 9 − j13 Ω ⇒ Ylca = 0.04 + j0.0533 f
Once we know the admittances we know,
ab
Gab
l = 0.03, Bl = −0.0710
bc
Gbc
l = 0.12, Bl = −0.16
ca
Gca
l = 0.04, Bl = 0.0533
1
bc
Bγab = −Blab + √ (Gca
l − Gl ) = 0.0248 f
3
1
ca
Bγbc = −Blbc + √ (Gab
l − Gl ) = 0.1540 f
3
1
ab
Bγca = −Blca + √ (Gbc
l − Gl ) = −0.0011 f
3
Total admittances are:
Y ab = Ylab + Yγab = 0.03 − j0.0462 f
Y bc = Ylbc + Yγbc = 0.12 − j0.006 f
Y ca = Ylca + Yγca = 0.04 + j0.0522 f
Knowing these total admittances, we can find line currents using following expressions.
Current Before Compensation
111
I a = I abl − I cal = (1 − α2 )Ylab − (α − 1)Ylca V = 0.2150 V ∠−9.51o A
I b = I bcl − I abl = (α2 − α)Ylbc − (1 − α2 )Ylab V = 0.4035 V ∠−161.66o A
I c = I cal − I bcl = (α − 1)Ylca − (α2 − α)Ylbc V = 0.2358 V ∠43.54o A
Powers Before Compensation
Sa
Sb
Sc
Total real power, P
Total reactive power, Q
Power factor in phase-a, pfa
Power factor in phase-b, pfb
Power factor in phase-c, pfc
V a (I al )∗ = Pa + jQa = V (0.2121 + j0.0355)
V b (I bl )∗ = Pb + jQb = V (0.3014 + j0.2682)
V c (I cl )∗ = Pc + jQc = V (0.0552 + j0.2293)
Pa + Pb + Pc = V 0.5688 W
Qa + Qb + Qc = V 0.5330 VAr
cos φa = cos(9.51o ) = 0.9863 lag
cos φb = cos(41.63o ) = 0.7471 lag
cos φc = cos(76.45o ) = 0.2334 lag
=
=
=
=
=
=
=
=
Thus we observe that the phases draw reactive power from the lines and currents are unbalanced
in magnitude and phase angles.
After Compensation
I a = I ab − I ca = (1 − α2 )Y ab − (α − 1)Y ca V = 0.1896 V ∠0o A
I b = I bc − I ab = (α2 − α)Y bc − (1 − α2 )Y ab V = 0.1896 V ∠−120o A
I a = I ca − I bc = (α − 1)Ylca − (α2 − α)Y bc V = 0.1896 V ∠120o A
Powers After Compensation
Sa
Sb
Sc
Total real power, P
Total reactive power, Q
Power factor in phase-a, pfa
Power factor in phase-b, pfb
Power factor in phase-c, pfc
=
=
=
=
=
=
=
=
V a (I al )∗ = Pa + jQa = V (0.1986 + j0.0)
V b (I bl )∗ = Pb + jQb = V (0.1986 + j0.0)
V c (I cl )∗ = Pc + jQc = V (0.1986 + j0.0)
Pa + Pb + Pc = (V × 0.5688 )W
Qa + Qb + Qc = 0 VAr
cos φa = cos(0o ) = 1.0
cos φb = cos(0o ) = 1.0
cos φc = cos(0o ) = 1.0
From above results we observe that after placing compensator of suitable values as calculated
above, the line currents become balanced and have unity power factor relationship with their voltages.
112
Example 3.6 Consider the following 3-phase, 3-wire system. The 3-phase voltages are balanced
sinusoids with RMS value of 230 V at 50 Hz. The load impedances are Za = 3 + j 4 Ω, Zb =
5 + j 12 Ω, Zc = 12 − j 5 Ω. Compute the following.
1. The line currents I la , I lb , I lc .
2. The active (P ) and reactive (Q) powers of each phase.
3. The compensator susceptance ( Bγab , Bγbc , Bγca ), so that the supply sees the load balanced and
unity power factor.
4. For case (3), compute the source, load, compensator active and reactive powers (after compensation).
N
Vsa
I la
Vsc
I lc
Vsb
I lb
a
c
Zb
Fig. 3.15 An unbalanced three-phase three-wire star connected load
Solution:
Given that Za = 3 + j 4 Ω, Zb = 5 + j 12 Ω, Zc = 12 − j 5 Ω.
1. Line currents I la , I lb , andI lc are found by first computing neutral voltage as given below.
V nN =
1
( Z1a
+
1
Zb
+
Va
1 (
) Za
Zc
=
=
=
Vb Vc
+
)
Zb
Zc
Va Vb Vc
Za Zb Zc
)(
+
+
)
Za Zb + Zb Zc + Zc Za Za
Zb
Zc
Zabc V a V b V c
(
+
+
)
∆Z Za
Zb
Zc
50∠97.82o
(24.12∠−99.55o )
o
252.41∠55.5
43.79 − j 67.04 V
80.75∠−57.15o V
= (
=
+
Now the line currents are computed as below.
113
V a − V nN
Za
230∠0o − 80.75∠−57.15o
=
3+j4
= 33.2 − j 21.65
= 39.63∠−33.11o A
I la =
V b − V nN
Zb
230∠−120o − 80.75∠−57.15o
=
5 + j 12
= 15.85∠152.21o A
I lb =
V c − V nN
Zc
230∠120o − 80.75∠−57.15o
=
12 − j 5
= 23.89∠143.35o A
I lc =
2. Active and Reactive Powers
For phase a
Pa = Va Ia cos φa = 230 × 39.63 × cos(33.11o ) = 7635.9 W
Qa = Va Ia sin φa = 230 × 39.63 × sin(33.11o ) = 4980 VAr
For phase b
Pb = Vb Ib cos φb = 230 × 15.85 × cos(−152.21o − 120o ) = 140.92 W
Qb = Vb Ib sin φb = 230 × 15.85 × sin(−152.21o − 120o ) = 3643.2 VAr
For phase c
Pc = Vc Ic cos φc = 230 × 23.89 × cos(−143.35o + 120o ) = 5046.7 W
114
Qc = Vc Ic sin φc = 230 × 23.89 × sin(−143.35o + 120o ) = −2179.3 VAr
Total three phase powers
P = Pa + Pb + Pc = 12823 W
Q = Qa + Qb + Qc = 6443.8 VAr
3. Compensator Susceptance
First we convert star connected load to a delta load as given below.
Zlab =
Za Zb +Zb Zc +Zc Za
Zc
Zlbc =
∆Z
Za
= 50.44 + j 2.08 = 50.42∠2.36o Ω
Zlca =
∆Z
Zb
= 19.0 − j 4.0 = 19.42∠ − 11.89o Ω
= 4 + j 19 = 19.42∠77.11o Ω
The above implies that,
ab
Ylab = 1/Zlab = Gab
l + j Bl = 0.0106 − j0.050 f
bc
Ylbc = 1/Zlbc = Gbc
l + j Bl = 0.0198 − j0.0008 f
ca
Ylca = 1/Zlca = Gca
l + j Bl = 0.0504 + j0.0106 f
From the above, the compensator susceptances are computed as following.
Bγab = −Blab +
−Gbc
(Gca
l )
l √
3
= 0.0681 f
Bγbc = −Blbc +
(Gab
−Gca
l √
l )
3
= −0.0222 f
Bγca = −Blca +
(Gbc
−Gab
l √
l )
3
= −0.0053 f
Zγab = −j 14.69 Ω (capacitance)
Zγbc = j 45.13 Ω (inductance)
Zγca = j 188.36 Ω (inductance)
115
4. After Compensation
0
Zlab = Zlab || Zγab = 24.97 − j 41.59 = 48.52∠ − 59.01o Ω
0
Zlbc = Zlbc || Zγbc = 21.52 − j 24.98 = 32.97∠49.25o Ω
0
Zlca = Zlca || Zγca = 24.97 − j 41.59 = 19.7332∠ − 6.0o Ω
Let us convert delta connected impedances to star connected.
Za =
=
=
Zb =
=
=
Zc =
=
=
Zab0 × Zca0
Zab0 + Zbc0 + Zca0
9.0947 − j 10.55
13.93∠ − 49.25o Ω
Zbc0 × Zab0
Zab0 + Zbc0 + Zca0
23.15 + j 2.43
23.28∠6.06o Ω
Zca0 × Zbc0
Zab0 + Zbc0 + Zca0
4.8755 + j 8.12
9.47∠59.01o Ω
The new voltage between the load and system neutral after compensation is given by,
1
0
V nN =
( Z1a
1
Zb
Va
1 (
) Za
Zc
o
+ +
= 205.42∠−57.15 V
+
Vb Vc
+
)
Zb
Zc
Based on the above, the line currents are computed as following.
0
Ia =
=
Ib =
=
V a − V nN
Za
18.58∠0o A
0
V b − V nN
Zb
18.58∠ − 120o A
0
Ic
V c − V nN
=
Zc
= 18.58∠120o A
116
Thus, it is seen that after compensation, the source currents are balanced and have unity power
factor with respective supply voltages.
Source powers after compensation
Pa = Pb = Pc = 230 × 18.58 = 4272.14 W
P = 3Pa = 12820.2 W
Qa = Qb = Qc = 0
Q = 0 VAr
Compensator powers
ab
Sγ
ab ∗
= V ab (I γ )
∗
∗
= V ab (V ab .Yγab )
2
= V ab Yγab
∗
√
= (230 × 3)2 × (−j 0.0068)
= −j 10802 VA
bc
Sγ
ca
Sγ
= Vbc2 Yγbc
∗
√
= (230 × 3)2 × (j 0.0222)
= j 3516 VA
= Vca2 Yγca ∗
√
= (230 × 3)2 × (j 0.0053)
= j 842 VA
References
[1] A. Ghosh and G. Ledwich, Power quality enhancement using custom power devices. Kluwer
Academic Pub, 2002.
[2] T. J. E. Miller, Reactive power control in electric systems.
Wiley, 1982.
[3] L. Gyugyi, “Reactive power generation and control by thyristor circuits,” IEEE Transactions
on Industry Applications, no. 5, pp. 521–532, 1979.
117
[4] R. Otto, T. Putman, and L. Gyugyi, “Principles and applications of static, thyristor-controlled
shunt compensators,” IEEE Transactions on Power Apparatus and Systems, no. 5, pp. 1935–
1945, 1978.
[5] N. Hingorani and L. Gyugyi, Understanding FACTS: Concepts and Technology of Flexible AC
Transmission Systems, 2000. Wiley-IEEE Press, 1999.
118