Download A Demonstration that Quotient Spaces of Locally Compact Hausdorff

A Demonstration that Quotient Spaces of
Locally Compact Hausdorff Spaces are k-Spaces
Sean E. Parrott-Wolfe
Department of Mathematics
of Lesley University
Cambridge, Massachusetts
May 22, 2011
Abstract
In this paper, we construct a proof that a space is compactly generated if and only if it is
the quotient of some locally compact Hausdorff space.
i
List of Notation
is an element in
∈
is contained in or is equal to
⊆
The closed interval from a to b
[a, b]
The set containing x
{x}
The empty set
{∅}
The closure of X
X
The complement of X in Y
Y −X
The union of sets X and Y
X ∪Y
n
[
U
The union of sets Ui over all values of i from 1 to n
i=1
The intersection of sets X and Y
The intersection of sets Ui over all values of i from 1 to n
X ∩Y
n
\
U
i=1
−1
The inverse or preimage of f
f
The function f that is a map from a set X to set Y
X→Y
The map from element p to element q
p 7−→ q
⇐⇒
if and only if
∼
Relation
1
1
Introduction
The topological properties of locally compact Hausdorff spaces are widely studied, and are fairly
well understood. Quotient spaces on the other hand, behave somewhat strangely. It is somewhat
remarkable that the combination of the two produces something so precise as the k-space. Here,
we will build up from a basic level the definitions and theorems needed in the proof that quotient
spaces of compactly generated Hausdorff spaces are k-spaces, and that the converse is also true.
2
Topological Spaces
Definition 2.1. A topology is a pair (X, T) of set X and collection of subsets, T, such that
• ∅ and X are in T
• For any collection of subsets S ⊂ T, the union
[
U is in T.
U ∈S
• If U1 , . . . , Un are in T, then the intersection,
n
\
Ui is in T.
i=1
Definition 2.2. The closure of a set A is the minimal closed set containing A, denoted A.
Definition 2.3. A neighborhood of a point x in X is a subset N of X if for some r > 0 the closed
ball at center x, with radius r lies entirely inside N.
Corollary 2.4. The following statements are equivalent:
(a) x lies in each of its neighborhoods
(b) The intersection of two neighborhoods of x is a neighborhood of x
(c) If N is a neighborhood of x and if U is a subset of X containing N, then U is a neighborhood
of x
(d) If N is a neighborhood of x and if N∗ is the set {z ∈ N | N is a nbd of z}, then N∗ is a nbd of
x
Definition 2.5. Two sets X and Y are said to be disjoint if their intersection X ∩ Y = {∅}.
2
Definition 2.6. A collection A of subsets of a space X is said to cover X, or to be a covering
of X, if the union of the elements of A is equal to X. It is called an open covering of X if its
elements are open subsets of X. A subcovering is a subset C of A which is also a covering of X.
Definition 2.7. A topological space is compact if any of its open covers contains a finite part
which covers the space, that is, if every open cover has a finite subcover.
Definition 2.8. A space X is said to be locally compact at x if there is some compact subspace
C of X that contains a neighborhood of x. In general, if X is locally compact at each of its points,
X is said to be locally compact.
Definition 2.9. A function f : A → B is said to be injective or one-to-one if for each pair of
distinct points of A, their images under f are distinct. The function is said to be surjective or
ontoif every element of B is the image of some element of A under the function f . If f is both
injective and surjective, it is said to be bijective, or a one-to-one correspondence.
Definition 2.10. Let X and Y be topological spaces. A function f : X → Y is said to be
continuous if for each open subset V of Y , the set f −1 (V ) is an open subset of X.
3
Homeomorphisms
Definition 3.1. Let X and Y be topological spaces; let f : X → Y be a bijection. If both the function f and the inverse function f −1 : Y → X are continuous, then f is called a homeomorphism.
Definition 3.2. A Hausdorff space is a topological space X with the property that two distinct
points can always be surrounded by disjoint open sets.
We now combine several of the concepts we have touched upon and look at properties of locally
compact Hausdorff spaces. First, let it be said that any compact subset of a Hausdorff space is a
closed Hausdorff space.
Theorem 3.3. Let X be a topological space. Then X is locally compact Hausdorff if and only if
there exists a space Y satisfying the following conditions:
(1) X is a subspace of Y .
(2) The set Y − X consists of a single point.
3
(3) Y is a compact Hausdorff space.
If Y and Y ∗ are two spaces satisfying these conditions, then there is a homeomorphism of Y with
Y ∗ that equals the identity map on X.
Proof. Let Y and Y ∗ be two spaces satisfying conditions (1)-(3). Let p be the singleton point of
Y − X and let q be the singleton point of Y ∗ − X. Define φ : Y → Y ∗ by letting φ : p 7−→ q and
φ : X → X be the identity map on X. Then if U is open in Y , then φ(U ) is open in Y ∗ and thus φ
is a homeomorphism.
Suppose U does not contain p. Then φ(U ) = U . Since U is open in Y and is contained in X, it
is open in X. Because X is open in Y ∗ , U is also open in Y ∗ . Suppose that U contains p. Since
C = Y − U is closed in Y , it is compact as a subspace of Y . C is a compact subspace of X because it
is contained in X. So because X is a subspace of Y ∗ , C is also a compact subspace of Y ∗ . Because
Y ∗ is Hausdorff, C is closed in Y ∗ , so φ(U ) = Y ∗ − C is open in Y ∗ . Take an object, say {ω} that
is not a point of X and adjoin it to X, to form the set Y = X ∪ {ω}. Put a topology on the set Y
by defining the collection of open sets of Y to consist of
(1) all sets U that are open in X, and
(2) all sets of the form Y − C, where C compact subspace of X.
We need to verify that this collection is, in fact, a topology on Y . ∅ is open in X, and the space Y
is of the form Y − C. Checking that the intersection of two open sets is open, we have:
U1 ∩ U2
which is open in X,
(Y − C1 ) ∩ (Y − C2 ) = Y − (C1 ∪ C2 )
which is of the form Y − C, and
U1 ∩ (Y − C1 ) = U1 ∩ (X − C1 )
which is open in X
because C1 is closed in X. Checking that the union of any collection of open sets is open:
[
Uα = U
is open in X,
[
(Y − Cβ ) = Y − (∩Cβ ) = Y − C
[
[
( Uα ) ∪ ( (Y − Cβ )) = U ∪ (Y − C) = Y − (C − U ),
4
is of the form Y − C, and
is of the form Y − C
because C − U is a closed subspace of C and therefore compact.
Given any open set of Y , we show its intersection with X is open in X. If U is open in X, then
U ∩ X = U , which is open in X. Since Y − C is of the form Y − C, (Y − C) ∩ X = X − C, which is
also open in X. Any set open in X is open in Y by definition, and therefore X is a subspace of Y .
Let A be an open covering of Y . The collection A must contain an open set of the form Y − C,
since none of the sets open in X contain the point {α}. Take all the members of A different from
Y − C and intersect them with X; they form a collection of open sets of X covering C. Because C is
compact, finitely many sets cover C; the corresponding finite collection of elements of A will, along
with the element Y − C, cover all of Y . To show that Y is Hausdorff, let x and y be two points of
Y . If x and y are in X, then there are open sets U containing x and V containing y, both open in
X, which are disjoint. Antithetically, if x in X and y = α, then we can choose a compact set C in
X containing a neighborhood U of x. So U and Y − C are disjoint neighborhoods of x which are in
Y , therefore Y is compact.
Conversly suppose a space Y satisfying conditions (1) through (3) exists. Then X is Hausdorff
since it is a subspace of the Hausdorff space Y .
Choose disjoint open sets U, V ⊆ Y with U containing x and V containing the singleton point
of Y − X. Then the set C = Y − V is closed in Y , so it is a compact subspace of Y . Since C is in
X, it is also compact as a subspace of X, and C contains the neighborhood U of x, so X is locally
compact at x.
Definition 3.4. A set X is said to be regular if for any point x and any closed set B disjoint from
x, there exist open sets containing x and B which are disjoint. A space is said to be completely
regular if singleton sets are closed in X and if for any point x and any closed set B disjoint from
x, there is a continuous function f : X → [0, 1] such that f (x) = 1 and f (B) = {0}.
Given this definition, a locally compact Hausdorff space is completely regular. A closed subset of
a locally compact space is locally compact and an open subset of a locally compact Hausdorff space
5
is locally compact.
Definition 3.5. A subset A of a topological space X is said to be precompact in X if A is compact.
This leads us to the following lemma:
Lemma 3.6. Let X be a locally compact Hausdorff space. Then for any x ∈ X, every neighborhood
U of x contains a compact neighborhood V of x, that is V ⊆ U .
Proof. Suppose U is a neighborhood of x. If W is any precompact neighborhood of x, then W − U
is closed in W and therefore compact. Because compact subsets can be separated by open subsets
in a Hausdorff space, there are disjoint open subsets Y containing x and Y ∗ containing W − U . Let
V = Y ∩ W . Because V ⊆ W , V is compact.
Since V ⊆ Y ⊆ (X − Y ∗ ), then we know that V ⊆ Y ⊆ (X − Y ∗ ), and so V ⊆ (W − Y ∗ ). Then
since (W − U ) ⊆ Y ∗ , (W − Y ∗ ) ⊆ U , and therefore V ⊆ U .
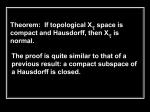
Proposition 3.7. Any open or closed subset of a locally compact Hausdorff space is a locally compact
Hausdorff space.
Proof. Let X be a locally compact Hausdorff space. Note that every subspace of X is Hausdorff,
so we only need to prove local compactness. If Y ⊆ X is open, Lemma X says that any point in Y
has a neighborhood whose closure is compact and contained in Y , so Y is locally compact. Suppose
Z ⊆ X is closed. Any x ∈ Z has a precompact neighborhood U ⊆ X. Since U ∩ Z is a closed subset
of the compact set U , it is compact. Since (U ∩ Z) ⊆ Z = Z, it follows that U ∩ Z is a precompact
neighborhood of x ∈ Z. Thus Z is locally compact.
At this point, it seems appropriate to mention Urysohn’s Lemma, and its relation to locally
compact Hausdorff spaces.
Theorem 3.8. (Urysohn’s lemma)Let X be a normal space; let A and B be disjoint closed
subsets of X. Let [a, b] be a closed interval in the real line. Then there exists a continuous map
f : X → [a, b] such that f (x) = a for every x in A, and f (x) = b for every x in B.
Corollary 3.9. (Urysohn’s Lemma, Locally Compact Hausdorff version)Let X be a locally
compact Hausdorff space. Let C be a compact subset of X and let Y be an open subset of X such
6
that C ⊆ Y . Then there exists a continuous function f : X → [0, 1] such that f [C] = {1} and f = 0
outside a compact subset of Y .
4
Quotient Spaces
Definition 4.1. An equivalence relation on a set A is a relation γ on A having the following
properties:
(i) (Reflexive) x ∼ x for each x ∈ A
(ii) (Symmetric) x ∼ y ⇐⇒ y ∼ x for each x, y ∈ A
(iii) (Transitive) If x ∼ y, and y ∼ z, then x ∼ z
Given an equivalence relation ∼ on a set A and an element x of A, we define a subset E of A, called
the equivalence class determined by x, by the equation
E = {y | y ∼ x}
(4.1)
Theorem 4.2. (Fundamental Theorem of Equivalence Classes)An equivalence relation ∼ on
a set X partitions X. Conversely, corresponding to any partition of X, there exists an equivalence
relation ∼ on X.
Proof. In both cases, the cells of the partition of X are the equivalence classes of X by ∼. Since each
element of X belongs to a unique partition of any partition of X, and since each cell of the partition
is identical to an equivalence class of X by ∼, each element of X belongs to a unique equivalence
class of X by ∼. Thus there is a natural bijection from the set of all possible equivalence relations
on X and the set of all partitions of X.
Definition 4.3. Let X and Y be topological spaces; let p : X → Y be a sujective map. The map p
is said to be a quotient map provided a subset U of Y is open in Y iff p−1 (U ) is open in X.
Definition 4.4. If X is a space and A is a set and if p : X → A is a surjective map, then there
exists exactly one topology T on A relative to which p is a quotient map; it is called the quotient
topology induced by p.
7
Definition 4.5. Let X be a topological space, and let X ∗ be a partition of X into disjoint subsets
whose union is X. Let p : X → X ∗ be the surjective map that carries each point of X to the element
of X ∗ containing it. In the quotient topology induced by p, the space X ∗ is called a quotient space
of X.
Definition 4.6. A set X/ ∼ with the quotient topology is called the quotient space of X by
partition ∼.
Remark 4.7. Following are two relavent properties of quotient spaces that bear mentioning.
Separation: If the quotient map ψ : X → X/S is open then X/S is a Hausdorff space if and
only if S is a closed subset of the product space X × X. The quotient space X/S is Hausdorff if
and only if any two elements of S possess disjoint saturated neighborhoods. Subset S is said to be
saturated if S contains every set ψ −1 ({y}) that it intersects.
Compactness If a space is compact, then so are all its quotient spaces; however a quotient
space of a locally compact space need not be locally compact.
Theorem 4.8. Suppose f : X → Y is a continuous surjective function. If X is compact and Y is
Hausdorff, then f is a quotient map.
Proof. Let C be a closed subset of X. A closed subset of a compact space is compact, so C is
compact. The continuous image of a compact set is compact, so f (C) is a compact subset of Y . A
compact subset of a Hausdorff space is closed. So f (C) is closed in Y .
Theorem 4.9. Let p : X → Y be a quotient map. Let Z be a space and let g : X → Z be a map that
is constant on each set p−1 (y), for y ∈ Y . Then g induces a map f : Y → Z such that f ◦ p = g.
The induced map f is continuous if and only if g is continuous; f is a quotient map if and only if
g is a quotient map.
Proof. For each y ∈ Y , the set g(p−1 ({y})) is a onepoint set in Z (since g is constant on p−1 (y)).
If we let f (y) denote this point, then we have defined amap f : Y → Z such that for each x ∈ X,
f (p(x)) = g(x). If f is continuous, then g = f ◦ p is continuous. Conversely, suppose g is continuous.
Given an open set V of Z is open in X. But g −1 (V ) = p−1 (f −1 (V )); because p is a quotient map,
8
it follows that f −1 (V ) is open in Y . Hence f is continuous.
If f is a quotient map, then g is the composite of two quotient maps and is thus a quotient map.
Conversely, suppose that g is a quotient map. Since g is surjective, so is f . Let V be a subset of Z;
we show that V is open in Z if f −1 (V ) is open. Now the set p−1 (f −1 (V )) is open in X because p
is continuous. Since this set equals g −1 (V ), the latter is open in X. Then because g is a quotient
map, V is open in Z.
Corollary 4.10. Let g : X → Z be a surjective continuous map. Let X ∗ be the following collection
of subsets of X:
X ∗ = {g −1 ({z}) | z ∈ Z}
(4.2)
Give X ∗ the quotient topology.
(a) The map g induces a bijective continuous map f : X ∗ → Z, which is a homeomorphism if and
only if g is a quotient map.
(b) If Z is Hausdorff, so is X ∗
Proof. By the preceding theorem, g induces a continuous map f : X ∗ → Z; it is clear that f is
bijective. Suppose that f is a homeomorphism. Then both f and the projection map p : X → X ∗
are quotient maps, so that their composite q is a quotient map. Conversely, suppose that g is a
quotient map. Then it follows from the preceding theorem that f is a quotient map. Being bijective,
f is thus a homeomorphism. Suppose Z is Hausdorff. Given distinct points of X ∗ , their images
under f are distinct and thus possess disjoint neighborhoods U and V . Then f −1 (U ) and f −1 (V )
are disjoint neighborhoods of the two given points of X ∗ .
Theorem 4.11. Let p : A → B and q : C → D be quotient maps. If B and C are locally compact
Hausdorff spaces, then p × q : A × C → B × D is a quotient map.
Proof. p × q is the composition
p×1
1×q
A × C −→ B × C −→ B × D
so as the compsition of two quotient maps, p × q is itself a quotient map.
9
(4.3)
5
k-Spaces
Definition 5.1. A topological space X is said to be compactly generated if for a subset U of
X, U is open if and only if U ∩ K is open in K for every compact subset K. If X is also Hausdorff,
then it is called a k-space.
Theorem 5.2. A space is locally compactly generated if and only if it is a quotient of a locally
compact space.
Proof. Disjoint sums of equivalence classes of locally compact spaces form locally compact spaces.
Theorem 5.3. Every locally compact space is a k-space.
Proof. Suppose X is locally compact and A ∩ K is open in K for each compact K contained in X.
Let a ∈ A and let V be an open neighborhood of a with compact closure. Then A intersection V is
open in V and hence A ∩ V = (A ∩ V ) ∩ V is open in V and thus in X. Then a has a neighborhood
contained in A, so A is open in X.
We now have enough to prove our final theorem.
Theorem 5.4. A space is compactly generated if and only if it is a quotient of a locally compact
Hausdorff space. In other words, quotient spaces of locally compact Hausdorff spaces are compactly
generated, and conversely, every compactly generated Hausdorff space is a quotient of some locally
compact Hausdorff space.
Proof. Let X be a locally compact Hausdorff space and let S be a subset of X. Then S is a locally
compact Haussdorff space by Proposition 3.7, as well. The quotient space of a Hausdorff space
is also Hausdorff, therefore X/S is a locally compact Hausdorff space. and by Theorem 5.3, X/S
is compactly generated. Conversely, the sum of disjoint compact Hausdorff spaces forms a locally
compact Hausdorff space, so every compactly generated space must be the quotient of some space
X, which is locally compact Hausdorff.
10
Acknowledgments
Thanks to my advisor and friend, Steven R. Benson for reawakening my love of mathematics, and
to Kaley Littlefield for her unending support.
11
References
[1] J. M. Lee, Introduction to Topological Manifolds, 2nd Ed. Springer, 2010.
[2] J. R. Munkres, Topology, 2nd Ed. Prentice Hall, 2000.
[3] O. Y. Viro, O. A. Ivanov, N. Y. Netsvetaev, V. M. Kharlamov, Elementary Topology: Problem
Textbook, AMS, 2008.
12