Download Week_2 - Staff Web Pages

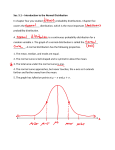
Week 2
Normal Distributions, Scatter
Plots, Regression and Random
The Normal Model
Density Curves and
Normal Distributions
A Density Curve:
• Is always on or above the x axis
• Has an area of exactly 1 between the
curve and the x axis
• Describes the overall pattern of a
distribution
• The area under the curve above any range
of values is the proportion of all the
observations that fall in that range.
Mean vs Median
• The median of a density curve is the equal
area point that divides the area under the
curve in half
• The mean of a density function is the
center of mass, the point where curve
would balance if it were made of solid
material
Normal Curves
•
•
•
•
•
Bell shaped, Symmetric,Single-peaked
Mean = µ

Standard deviation =
Notation N(µ,  )
One standard deviation on either side of µ
is the inflection points of the curve
68-95-99.7 Rule
• 68% of the data in a normal curve at least
is within one standard deviation of the
mean
• 95% of the data in a normal curve at least
is within two standard deviations of the
mean
• 99.7% of the data in a normal curve at
least is within three standard deviations of
the mean
Why are Normal Distributions
Important?
• Good descriptions for many distributions of
real data
• Good approximation to the results of many
chance outcomes
• Many statistical inference procedures are
based on normal distributions work well for
other roughly symmetric distributions
Standardizing
Standardizing (z-score)
• We standardize to compare items from
more than one distribution. (Apples and
Oranges)
• A z score is the number of standard
deviations off center (mean) a data item is.
To Find a z score
• Subtract the mean from the item.
• Divide the result by the standard deviation
z
x 

Standard Normal Curve
Standard Normal Distribution
• A normal distribution with µ = 0 and
 N(0,1) is called a Standard Normal
1,
distribution
• Z-scores are standard normal where
z=(x-µ)/ 
=
Standard Normal Tables
• Table B (pg 552) in your book gives the percent of the
data to the left of the z value.
• Or in your Standard Normal table
• Find the 1st 2 digits of the z value in the left column and
move over to the column of the third digit and read off
the area.
• To find the cut-off point given the area, find the closest
value to the area ‘inside’ the chart. The row gives the
first 2 digits and the column give the last digit
Solving a Normal Proportion
• State the problem in terms of a variable (say x) in the
context of the problem
• Draw a picture and locate the required area
• Standardize the variable using z =(x-µ)/
• Use the calculator/table and the fact that the total area
under the curve = 1 to find the desired area.
• Answer the question.

Finding a Cutoff Given the Area
• State the problem in terms of a variable
(say x) and area
• Draw a picture and shade the area
• Use the table to find the z value with the
desired area
• Go z standard deviations from the mean in
the correct direction.
• Answer the question.
Assessing Normality
• In order to use the previous techniques the
population must be normal
• To assessing normality :
 Construct a stem plot or histogram and see if
the curve is unimodal and roughly symmetric
around the mean
Normal Probability Calculator
• http://www.math.hope.edu/swanson/statla
bs/stat_applets.html
Scatterplots, Association
and Relationships
How are two quantitative variables
related?
Variables
• Response Variable: measures the
outcome of a study (y variable, dependent
variable, the “result”)
• Explanatory or Predictor Variable
attempts to explain the observed
outcomes (x variable, independent
variable, the “cause”)
Scatterplot
• Shows the relationship between two
variables measured on the same
individual.
• Graph the explanatory variable on the
horizontal axis. (x list)
• Graph the response variable on the
vertical axis (y list)
Interpreting Scatterplots
• Overall pattern
 Direction (increasing or decreasing ?)
 Form (linear, exponential?)
 Strength of relationship
 The width of the hallway
• Outliers and Influencial Points
 What does not fit the pattern
 Falls outside the usual values of either
variable
Direction (Think Slope)
• Two variables are positively associated
when the above average values of one are
associated with the above average values
of the other.
• Two variables are negatively associated
when the above average values of one are
associated with the below average values
of the other
Form
• Form is the general shape of the dots in
the scatterplot
• Linear, exponential, logarithmic, . . .
• Correlation is ONLY relevant with linear
data.
• “Curved” data must be “straightened”
before we can use correlation
Strength
• How much is the data lined up.
• The closer to a straight line the stronger
the relationship
• Correlation is a measurement of the
strength of the relationship between
predictor and response variables
Correlation
How strong is the relationship
Correlation
• The average of the product of
standardized x’s and y’s
• NO! We will never use this formula!!!!!
xi  x yi  y
1
r
(
)(
)
n 1
sx
sy
• Thank you, Technology!!!
Correlation Facts
• It makes no difference which variable is
the x and which is the y
• Positive r indicates a positive association
between the variables and negative r
indicates a negative association
• -1 ≤ r ≤ 1 Values near zero indicate a weak
association. Values near 1 or -1 indicate
strong association
Correlation facts 2
• There are no units on r so it is immune to
changes when units change.
• Correlation measures the strength of
ONLY linear relationships.
• Do not use correlation describe curved
relationships
• Correlation is greatly affected by extreme
values
Correlation Facts 3
• Outliers can make a strong relationship
look weak
• Outliers can make a weak relationship
look strong
• Report the correlation both with and
without the outlier(s)
Conditions for Correlation
• The quantitative condition: Both variables must be
quantitative.
• The linear condition: The form of the relationship must
be linear.
• The outlier condition: Outliers greatly affect
correlation. Report the r value both with and without the
outliers factored in
Linear Regression
Can we predict a result from our
data?
Modeling quantitative variable
relationships
• We want to be able to predict one
quantitative variable if we are given the
other.
• We will use a line as our model
• This line is called the line of best fit or the
Least Squares Regression Line(LSRL)
Theory of LRSL
• If we draw a line through our data not all of
the data points lie on the line.
• So, there is some error in our prediction
model.
• It follows that we want the best line and
the best line is the one with the least error
Theory page 2
• It follows then that we need a measure of
the error.
• We will define our error to be the observed
value (point) minus the predicted value
(line) and call this error the residual
• Residual = observed - predicted
Theory page 3
• The “best” line would be the one with the
smallest total of the residuals
• Problem: The residuals can be both
positive (line too low) or negative (line too
high) so the best line would have a total of
zero no matter how good the model was.
• Solution: Square the residuals before
totaling
Theory page 4
• So, if we try a graphic representation we
are placing square between each data
point and the prediction line.
• Big Finish
• So, the line that is the best fit to the data is
the line with the least total area of the
squares. Hence the name Least Squares
Regression Line
Finding the LSRL
• The LSRL always goes through the point
(x-bar,y-bar), the average of the x’s and
the average of the y’s)
• Move one standard deviation (Sx) in the x
direction moves us r standard deviations
(Sy) in the y direction.
LSRL
• To write the equation of a line we need the
slope and a point.
rsy
Slope 
sx
point  (x, y )
• Now use your Algebra I skills to create the line

Interpreting the LSRL
• Example: Price = -500(age) + 2000
• Slope = -500 tells us that if age increases by
one year the price decreases by 500 dollars
• 2000 tells us that if the age was zero (new) the
price was 2000
Interpreting the LSRL
• Example2: Verbal = .9(Math) + 200
• Slope = .9 tells us that if the math score
increases by one point the verbal score
increases by .9 of a point
• 200 tells us that if the math score was zero the
verbal score would be 2000
R squared
• r2 is the Coefficient of Determination
• It is the percent of the variation in the y values
that can be explained by the difference in the x
values in the prediction line
• An r2 = .7 means that 70% of the change in the
y value can be attributed to the change in the x
value in the LSRL
Assumptions
• In order for a LSRL to be valid there are
three conditions:
 Both Quantitative variables
 The scatterplot is “straight enough”
 Outliers can have a large effect
Regression tool
• http://science.kennesaw.edu/~plaval/tools/
regression.html
Understanding
Randomness
Random
• An event is random if:
• it is impossible to predict what the next
result of the event will be.
• Results are independent.
• Events that are random are ones where
all sequences of results of the event are
equally likely to occur.
• Random does NOT mean haphazard.
Randomness is Important
• The use of randomness is vital to the
modern study of statistics. Without which
we can not do many of the techniques of
modern statistical analysis.
Sources of Random Numbers
• Random number tables. Table A Page
550 in the back of our book.
• Computer Software
• Calculator: RandInt (low, high, HowMany)