Download Document

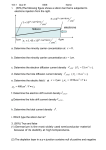
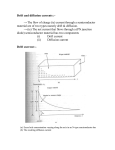
Carrier Transport Phenomena
• Random Motion is due to the interaction
between charged carriers and ionized impurities
atoms and vibrating lattice atoms.
• Scattering process: Collision of carriers with
ionized impurity atoms (called ionized impurity
scattering), and thermally vibrating lattice atoms
(called phonon or lattice scattering).
Carrier Transport Phenomena
Random motion of carriers
without applied field
No net carrier displacement
Random thermal velocity, vth
1 * 2 3
m vth =
kT = 6.2245 × 10 − 21 J
2
2
Random motion as well as a net
movement along the direction of field
Net carrier displacement and
thus a net velocity along the
field.
This velocity is called the drift velocity,
which gives drift current.
Charged Carriers Collisions
• Mean scattering time τ:
is the average time
between the two
collisions.
• During this time the
carriers moves an
average distance l ,
called mean free path.
• Random thermal velocity,
vth, is the average velocity
between the collisions:
1 *2 3
m vth = KT = 6.2245×10−21J
2
2
Typical value of vth ∼ 107 cm/s
Drift mobility:
When an electric field is applied to the crystal, electrons and holes experience a
net acceleration in a direction in addition to its random motion. As the charged
particle accelerates, the velocity increases and then it suddenly collide with a
vibrating atom and loses the gained velocity. The particle will again begin to
accelerate and gain energy until it is again involved in a scattering process.
Throughout this process the particle will gain an average drift velocity.
Average drift velocity (for low fields), <vd>= (eτ / m* )E = µE
µ is called mobility (cm2/ V-s):
Mobility:
μ=
eτ
m*
Drift Current Density:
If we have a positive volume charge density ρ moving with an average drift
velocity vd, the drift current density,
I
j =
A
Current
J drift = ρvd
density
Charge Density ρ = −en
or
For example if the volume charge density
is due to holes then:
For low electric fields, the drift
velocity is proportional to the
electric field.
Where μ is the proportionality factor and is
called the hole mobility. Its unit is cm2/ V-s
C / cm2 − s or Amp/ cm2
= ep
J p = epv dp
vdp = μ p E
Therefore:
J p = eμ p pE
Drift Current density
Similarly the drift current density due to electrons is,
J n = eμ n nE
Since both electrons and holes contribute to the drift current, the total drift
current density is,
J drf = e( μ n n + μ p p ) E = σE
σ = e ( nμ n + pμ p )
Conductivity:
Where σ is the conductivity of the semiconductor material. Its unit is Ω-1 cm-1
The reciprocal of conductivity is resistivity ρ,
ρ=
1
σ
=
1
.
e( nμ n + pμ p )
For intrinsic material,
σ = e( nμ n + pμ p ) = e( μ n + μ p ) n i
For n type material, n >> p. therefore,
σ = e ( n μ n + p μ p ) ≅ eμ n n
For p type material, p >> n. therefore,
σ ≅ eμ p p
(Assuming that μn and μp are comparable)
Temperature dependence of mobility
There are two collisions or scattering mechanisms that dominate in a
semiconductor and affect the carrier mobility:
(1) Phonon or lattice scattering and
(2) Ionized impurity scattering.
Phonon or lattice scattering:
The thermal energy at temperature above absolute zero causes the atoms to
randomly vibrate about their lattice position within the crystal. Charged carriers
collide with vibrating atoms and are scattered. The lattice scattering increases
with temperature and thus mobility decreases.
μ L ∝ T −3 2
Ionized impurity scattering:
A coulomb interactions between the electrons or holes and the ionized impurities
cause collisions and the scattering of the carriers. As the temperature increases
this type of scatterings decreases, increases the mobility:
T32
μI ∝
NI
N I = N d+ + N a−
NI is concentration of
the ionized carries
Temperature dependence of
mobility:
Scattering time:
dt
τ
=
dt
τI
+
dt
τL
dt/τ is the probability of a
scattering event occurring in
differential time dt. Now
recall:
μ=
eτ
m*
Therefore:
1
μ
=
1
μI
+
μ L ∝ T −3 2
1
μL
T32
μI ∝
NI
Doping dependence of mobility
As the doping levels in
semiconductors change, the
ionization scattering changes.
The mobility follows an
empirical relationship as:
μ (N ) = μ min +
μ0
1 + (N / N ref )
Parameters for silicon at 300K:
α
Velocity Saturation:
1 * 2 3
m vth =
KT
2
2
vd,sat ≈ vth ∼ 107 cm/s
Ref: D. A. Naeman, Semiconductor Physics and Devices
Example: Given: Si sample,
N d = 1017 cm −3
I) Calculate σ at 27ºC and 127ºC.
II) The above n-type is further doped with Na = 9 × 1016 cm-3, Calculate the
conductivity of the sample at 27ºC
Example: Consider the electron mobility in Si, μn = 1350 cm2/V-s and
. Calculate:
(1) The mean scattering time and (2) The mean free
path.
mn* = 0.26m0
Examples
An electron has a mobility of 1000 cm2/V-s at 300 K. if effective mass is 0.2 mo,
Calculate mean free time and mean free path of the electron.
If a silicon sample is doped with Nd = 2 x 1017 calculate the conductivity and the
resistivity of the sample at 300K and assuming full ionization.
Repeat your calculations for the case if the sample is doped with Nd = 2 x 1014.
Compare these values with experimental values.
If the sample in the above example has a 1 mm length and a 100 volts applied
on both sides of the sample calculate the drift current going through the
sample. Calculate the average drift velocity of the carries.
If Ge has an intrinsic mobility of 3900 for electrons and 1900 for holes
respectively, calculate the intrinsic conductivity and resistively of this material.
Carrier Diffusion:
Diffusion is the process whereby the thermal random motion of particles causes
them to flow from a region of high concentration toward a region of low
concentration.
Diffusion Current:
In semiconductor, the net flow of charge carriers (electrons or holes) results in a
diffusion current. The carrier diffusion current is proportional to the density
gradient or spatial derivative, thus the diffusion current density,
J dif ∝
dn
dp
=∝
dx
dx
For electrons,
For holes,
J n , dif = eDn
J p , dif = −eD p
dn
dx
dp
dx
D = vth l
Where νth is the thermal velocity and
l is the mean free path of the carrier
Where D is the diffusion coefficient, has units of cm2/s and is a positive quantity.
n(x)
p(x)
→ Electron current
← Electron diffusion
← hole current
← hole diffusion
x
x
Total Current Density:
dn
→ Electron current
dx
dp
→ Hole current
J p = epμ p E x − eD p
dx
The total current , J = J n + J p
J n = enμ n E x + eDn
J = enμ n E x + epμ p E x + eDn
dn
dp
− eD p
dx
dx
Example 5.3: Given: n-type GaAs at T = 300ºK. n(x) varies linearly from
1018 to 7×1017 cm-3 over a distance of 0.1cm. Calculate the diffusion current
density due to the electron diffusion. Assume Dn = 225 cm2/s.
Graded Impurity Concentration:
If the semiconductor is not uniformly doped, still it reaches thermal equilibrium
by diffusion and latter diffusion induced drift process.
Induced Electric Field:
Consider a semiconductor that is non uniformly doped with donor impurity atoms.
The doping concentration decreases as x increases as shown in the following
figure.
Ec
The electric field (induced) is defined as
Ex = −
dV ( x )
dx
V(x) = E(x)/e.
EF
EFi
Ev
1 dE ( x ) 1 d ( E F − E Fi ) 1 dE Fi
Ex =
=
=
e dx
e
dx
e dx
x
Again at thermal equilibrium the total
electron current is zero. Therefore,
1 dE Fi
Ex =
e dx
n0 ( x ) = ni e(E F − E Fi ) / kT
or , E F − E Fi = kT ln
or ,
Ex = −
n0 ( x )
ni
dE Fi
kT dn0 ( x )
=−
dx
n0 ( x ) dx
1 dn0 ( x )
kT
.
.
e n0 ( x ) dx
Assuming, n0 ( x ) = N d ( x )
dn0 ( x )
=0
dx
⎧ kT 1 dn0 ( x ) ⎫
dn0 ( x )
=0
or , n0 ( x ) μ n ⎨−
⎬ + Dn
(
)
dx
e
n
x
dx
0
⎩
⎭
kT
.μ n + Dn = 0
or , −
e
D
kT
∴ n =
μn
e
J n = en0 ( x ) μ n E x + eDn
Similarly ,
Thus ,
Ex = −
dN ( x )
1
kT
.
. d
e N d ( x)
dx
Dn
μn
Dp
μp
=
=
Dp
μp
kT
,
e
=
kT
e
Einstein relation
Example 5.4:
The total current in a semiconductor is constant and is composed of electron
drift current and hole diffusion current. The electron concentration is
constant and is equal to 1016 cm-3. The hole concentration is given by
p( x ) = 1015 e − x L
cm-3 ( x ≥ 0), where L =12 μm. Dp = 12 cm2/s and μn = 1000 cm2/V-s. The total
current density is J = 4.8 A/cm2. Determine (a) the hole diffusion current density
versus x, (b) Calculate electron drift current at x = 0 and (c) the electric field at x = L.
Hall effect:
Carriers experience a force, Fy = evx×Bz
eE H = ev x BZ
VH = E H W
I x Bz
p=
eVH d
IxL
μp =
epVxWd
Example 5.5:
Consider the geometry shown in previous page, determine the majority
carrier concentration and mobility based on the following data. L = 0.1 cm,
W = 0.01 cm, d = 0.001 cm, Ix = 0.75 mA, Vx = 15 V, Bz = 1000 gauss and
VH = 5.8 mV.
The unit of Bz is Tesla (MKS unit, weber/m2) or
gauss (CGS unit, Maxwell/cm2).
1 Tesla = 104 gauss.
1 Weber = 108 Maxwell.
Example:
In GaAs, Nd (x) = Nd0 exp(-x/L) for 0 ≤ x ≤ L, where L = 0.1 μm. and Nd0 = 5 ×
1016 cm-3. Assume μn = 6000 cm2/V-s and T =300 K. Derive the expression
for the electron diffusion current density versus distance over the given range
of x. (b) Determine the induced electric field that generates a drift current
density that compensates the diffusion current density.