Download Interior Angles of Polygons Plenty of Polygons

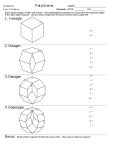
Interior Angles of Polygons
Plenty of Polygons
ACTIVITY
2.1
SUGGESTED LEARNING STRATEGIES: Summarize/Paraphrase/
Retell, Activating Prior Knowledge, Think/Pair/Share
My Notes
It is impossible to measure lengths and angles exactly; however, tools such
as rulers and protractors allow you to measure with reasonable accuracy.
In the diagram below, the sum of the measures of the five indicated angles
should be exactly 360°.
1. Measure the five angles and record each measure in the table below.
Then calculate the sum of the angle measures.
© 2010 College Board. All rights reserved.
1
m∠1
m∠2
2
3
5
4
m∠3
m∠4
m∠5
Sum
2. Compare your sum to the results of other students in your class. Are
the results always the same? If not, explain why differences can occur
and which answers are reasonably close.
Unit 2 • Congruence, Triangles, and Quadrilaterals
93
ACTIVITY 2.1
continued
Interior Angles of Polygons
Plenty of Polygons
My Notes
SUGGESTED LEARNING STRATEGIES: Think/Pair/Share,
Create Representations, Look for a Pattern, Self/Peer Revision
Your teacher will provide your group with a page containing polygons.
3. Measure, as precisely as possible, each interior angle, and record your
results below. Complete the table by calculating the indicated sums.
1st
2nd
3rd
4th
5th
6th
Angle Angle Angle Angle Angle Angle
MATH TERMS
A polygon is a closed
geometric figure with
sides formed by three or
more coplanar segments
that intersect exactly two
other segments, one at
each endpoint. The angles
formed inside the polygon
are interior angles.
Total
Triangle
Quadrilateral
Pentagon
Hexagon
4. Compare your results in the table with those of other groups in your
class. What similarities do you notice?
Triangle:
Quadrilateral:
Pentagon:
Hexagon:
Knowing that the sum of the measures of the interior angles of a triangle
is a constant and that the sum of the measures of non-overlapping angles
around a single point is always 360°, you can determine the sum of the
measures of any polygon without measuring.
94
SpringBoard® Mathematics with Meaning™ Geometry
© 2010 College Board. All rights reserved.
5. Write a conjecture about the sum of measures of the interior angles of
each of the polygons.
Interior Angles of Polygons
ACTIVITY 2.1
continued
Plenty of Polygons
SUGGESTED LEARNING STRATEGIES: Summarize/Paraphrase/
Retell, Think/Pair/Share, Create Representations, Look for a
Pattern, Quickwrite
6. Use auxiliary segments to determine a way to predict and verify
the exact sum of the angles of any quadrilateral and any pentagon.
Describe your methods so that another group would be able to
replicate your results for the pentagon.
My Notes
MATH TERMS
To replicate means to duplicate
or imitate. Notice the word
replica contained within the
word. In science, experiments
are designed so that they can be
replicated by other scientists.
7. Use the method you described in Item 6 to answer the following.
a. Explain how to determine the sum of the measures of the interior
angles of a hexagon.
b. Explain how to determine the sum of the measures of the interior
angles for any polygon.
© 2010 College Board. All rights reserved.
8. Use the method described in your answer to Item 7 to complete the
table below.
Polygon
Number of
Sides
Triangle
3
Quadrilateral
4
Pentagon
5
Calculations
Sum of the Measures
of the Interior Angles
Hexagon
Heptagon
Octagon
Nonagon
Decagon
Dodecagon
n-gon
n
Unit 2 • Congruence, Triangles, and Quadrilaterals
95
ACTIVITY 2.1
continued
Interior Angles of Polygons
Plenty of Polygons
My Notes
SUGGESTED LEARNING STRATEGIES: Think/Pair/Share,
Create Representations
9. Observe in Item 8 that as the number of sides increases by one, the
sum of the angle measures also increases by a constant amount. What
type of function models this behavior?
10. For the first six polygons in Item 8, plot the ordered pair (number of
sides, sum of angle measures) on the axes below. Carefully choose and
label your scale on each axis.
Write the equation in slopeintercept form:
y = mx + b
12. State the numerical value of the slope of the line in Item 11 and
describe what the slope value tells about the relationship between the
number of sides and the sum of the measures of the interior angles of
a polygon. Use units in your description.
96
SpringBoard® Mathematics with Meaning™ Geometry
© 2010 College Board. All rights reserved.
11. T he data points you graphed above should appear collinear.
Write an equation for the line determined by these points.
Interior Angles of Polygons
ACTIVITY 2.1
continued
Plenty of Polygons
SUGGESTED LEARNING STRATEGIES: Think/Pair/Share,
Create Representations
My Notes
13. If the function S represents the sum of the measures of the interior
angles as a function of the number of sides n, write an algebraic rule
for S(n).
14. Use S(n) to determine the value of S(7.5). For this value, explain the
significance, if any, given that S(n) represents the sum of the angle
measures of an n-sided polygon.
Linear functions have continuous domains consisting of all real numbers.
However, some contexts restrict the domain of linear functions. If the
graph of a linear model consists of discrete points, the linear function is
said to have a discrete domain.
15. What is the domain of S(n)?
© 2010 College Board. All rights reserved.
16. In a regular polygon, each interior angle has the same angle measure.
Based upon your results from the table in Item 8, determine the angle
measure in degrees of each interior angle for each regular polygon below.
Polygon
Number
of Sides
Sum of the
Measures of the
Interior Angles
(degrees)
Measure of
Each Interior
Angle
(degrees)
ACADEMIC VOCABULARY
A regular polygon is a polygon
that is both equiangular, with
all angles congruent, and
equilateral, with all sides
congruent.
Triangle
Quadrilateral
Pentagon
Hexagon
Heptagon
Octagon
Nonagon
Decagon
Dodecagon
n-gon
Unit 2 • Congruence, Triangles, and Quadrilaterals
97
ACTIVITY 2.1
continued
Interior Angles of Polygons
Plenty of Polygons
My Notes
SUGGESTED LEARNING STRATEGIES: Create
Representations, Look for a Pattern, Quickwrite
Interior Angle Measure
(in degrees)
17. For each regular polygon listed in the table in Item 16, plot the
ordered pair (number of sides, measure of each interior angle) on the
axes below. Carefully choose and label your scale on each axis.
Number of Sides
18. T he points plotted in Item 17 should not appear collinear. Explain
how that conclusion could have been drawn from the data alone.
TECHNOLOGY
Use the TABLE or GRAPHING
component of a graphing
calculator. Enter the algebraic
function for E(n) in y1 to
explore the measure of
individual angle measures
of a regular polygon as the
number of sides increase.
98
20. As n gets very large, what appears to be happening to the measure of
each angle? What causes this behavior?
SpringBoard® Mathematics with Meaning™ Geometry
© 2010 College Board. All rights reserved.
19. If the function E represents the measure of each interior angle as a
function of the number of sides n, write an algebraic rule for E(n).
Interior Angles of Polygons
ACTIVITY 2.1
continued
Plenty of Polygons
SUGGESTED LEARNING STRATEGIES: Think/Pair/Share,
Look for a Pattern
21. Determine the angle measures in the interior of the concave decagon.
The five acute angles are congruent, and the five reflex angles are
congruent.
My Notes
MATH TERMS
A concave polygon is a
polygon that has one or more
interior angles measuring more
than 180°.
A convex polygon is a polygon,
all of whose angles measure less
than 180°.
22. Does your function S(n) in Item 13 apply to this concave decagon?
Explain.
23. Does your function E(n) in Item 19 apply to this concave decagon?
Explain.
A concave polygon has sides that
appear to cave in. In a concave
polygon, like pentagon ABCDE
below, it is possible to draw a
line segment with endpoints in
the interior of the polygon such
that the segment contains points
in the exterior of the polygon.
A
C
© 2010 College Board. All rights reserved.
B
E
D
MATH TERMS
A reflex angle is an angle with a
measure greater than 180° and
less than 360°. To determine
the measure of a reflex angle,
use the fact that there are 360°
about a point in the plane.
You know how to measure the
related angle whose measure is
less than 180°.
Unit 2 • Congruence, Triangles, and Quadrilaterals
99
Interior Angles of Polygons
ACTIVITY 2.1
continued
Plenty of Polygons
CHECK YOUR UNDERSTANDING
Writeyour
youranswers
answersonon
notebook
paper.
Show your work.
Write
notebook
paper.
Show
5. If the sum of the measures of the interior angles of
your work.
a polygon is 2700°, how many sides does it have?
Determine the missing angle measure for each
polygon.
1.
100°
140°
k
2.
b. 15
c. 17
d. Not enough information
6. If the measure of each interior angle of a
polygon is 150°, how many sides does it have?
87°
108°
a. 9
a. 10
b. 12
c. 15
d. Not enough information
7. Given !APT with angle measures as labeled,
solve for x and calculate the three angle measures.
b
94°
P
18°
(6x + 1)°
3.
A
(5x - 17)°
(9x - 24)°
T
Draw polygons to satisfy the given conditions.
9. An equilateral hexagon that is not equiangular.
88°
(13x −3)°
(7x + 15)°
80°
10. A concave pentagon with a reflex angle
measuring 200°.
11. A regular polygon with an angle measuring 135°.
12. MATHEMATICAL As the number of sides of a
R E F L E C T I O N regular polygon increases,
what happens to the shape of the polygon?
100
SpringBoard® Mathematics with Meaning™ Geometry
© 2010 College Board. All rights reserved.
4.
8. An equiangular quadrilateral that is not
equilateral.