Download 9/13/07 Math 31 Handout: Section 3

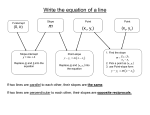
Math 125 Exam 1 Checklist and Focus Problems
Homework Due: Chapters 1, 2, 3 (except 2.4 and 3.4)
Calculators NOT allowed for this exam
Section
1.1
Focus Problems:
From the exercises at
the end of each section
11th Edition! (Warning!
I choose these
problems based on the
level for the exam. The
10th edition may not
reflect the same types
of problems.)
21
Key notes



1.2
1.3
47, 65, 79

81

11
37, 41, 47


65, 73
1.4
39
43, 45



2.1
21, 29

59


23, 33, 41
2.2
3, 7, 9

Know the following sets of numbers and how they relate to each other:
 Natural numbers
 Whole numbers
 Integers
 Rational numbers
 Irrational numbers
 Real numbers
Know the decimal representations of rational numbers (terminates or
repeats)
Know the decimal representation of irrational numbers (does not
terminate, does not repeat)
Be able to perform operations on real numbers:
Add, subtract, multiply, and divide integers, fractions, decimals
Division by zero is undefined
Work with positive exponents
Work with square roots (know all square roots of perfect squares up to
225
Use the order of operations to simplify expressions
Simplify algebraic expressions
Know the commutative, associative, distributive properties
Solve linear equations and know how to check your answers (by
substituting answer back into original equation)
Solve equations with fractions (clear denominators first)
Special cases:
 Equations which have solution set “all real numbers”
 Equations which have “no solution”
solution set is the empty set 
Solve formula for specified variable
1
2.3
2.5
7, 11
17
39


49, 55



13, 17, 29
37, 39
2.6
21, 23, 27
35, 45
2.7
9, 69
33, 41, 71, 73
93, 103
101
3.1
9













35
45, 49
3.2


25, 31



23

67, 69


Write algebraic expressions
Set up, solve, and answer application problems
 Remember to define your variable
 Remember to answer with the correct units of measurement and use a
complete sentence.
Solve interest and mixture problems
See Handout on Word Problems
Solve linear inequalities, write solution set using interval notation, and
graph on number line
 Note: the only time the inequality direction is reversed is when you
multiply or divide by a negative number
 Special cases:
If variable is eliminated in the process and the resulting statement is
true (such as 0 < 2), then the solution is all real numbers  ,  
If resulting statement is false (such as 5 < 3), then there is no solution,
solution set is 
Know the difference between “and” and “or”
Find solution set to compound inequalities
Solve compound inequalities, write final solution set using interval
notation, and graph
Know definition of absolute value (distance of a number from 0)
Solve absolute value equations
Solve absolute value inequalities
Be careful, sometimes the solution set is  ,   or 
Remember, first step is to isolate the absolute value.
See Summary Box on page 113, and Caution Box on page 115.
Know what an ordered pair (x, y) means and how to plot it on a
rectangular coordinate system.
Know the Quadrants (I, II, III, and IV).
Know: x-intercept is the point on the line that crosses the x-axis, yintercept is the point that crosses the y-axis.
Coordinates of x-intercept is (x,0); y-intercept is (0, y).
Determine the intercepts from an equation:
letting y = 0 gives the x -intercept, letting x = 0 gives the y - intercept.
Graph a line by using x and y intercepts
Identify the equations of a vertical and horizontal line, and graph them:
x = a is a vertical line, y = b is a horizontal line.
Know the formula for slope.
Know how to find the slope of a line, given two points.
Know what each type of slope looks like: positive slope, negative slope,
zero slope, undefined slope
Be able to identify the slopes of a horizontal line and a vertical line:
A horizontal line has slope = 0. A vertical line has undefined slope.
Using slopes, determine if lines are parallel, perpendicular, or neither.
Note: slopes of parallel lines are the same; slopes of perpendicular lines
are opposite reciprocals of each other
2
3.3
31
21
35, 61
45, 47
69, 71, 73
85









3.5
9, 11
27, 29, 31
3.6



5, 15, 19
23
31
37
45
51





Know the standard form of the equation of a line
Know the slope-intercept form of the equation of a line.
Know how to use the slope-intercept form to determine the line’s slope
and y-intercept, solving for y if necessary.
Graph a line using slope and y-intercept
Be able to write down the equation of a line given its slope and yintercept.
Example: Write down the equation of a line passing through (0, -5) with
slope 8. Answer: y= 8x – 5
Know the point-slope form of the equation of a line.
Know how to write the equation of a line using the point-slope form,
then rearrange to get the slope-intercept form or the standard form
Be able to write down the equation of a line given information about the
line and its relationship to another line.
Solve application problems.
See Handout on 3.3,
Know the definition of a function.
Be able to distinguish whether a relation is a function or not a function.
Know what the vertical line test says, and use it to determine whether a
graph represents a function.
Be able to determine the domain and range of a relation.
 Given a set of ordered pairs
 Given a graph
Understand function notation f(x)
 for equations
 for ordered pairs
 for graphs
Write equations of lines using function notation.
Graph and give domain and range of a linear function.
(Note that a horizontal line has range which is a single number).
3