Download Econ 281 Chapter 1

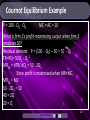
Econ 384
Intermediate
Microeconomics II
Lorne Priemaza, M.A.
[email protected]
Various material courtesy of
Wiley & Sons INC.
Chapter 13
13.1 Market Structure
13.2 Homogeneous Oligopoly
13.3 Dominant Firm Markets
13.4 Oligopoly with Horizontally Differentiated
Products
13.5 Monopolistic Competition
Appendix
13.1 Market Structure
Market structure depends upon two spectrums:
1) Number of firms in market
2) Product Differentiation
Definition: Product Differentiation between two
or more products exists when the products possess
attributes that, in the minds of consumers, set the
products apart from one another and make them
less than perfect substitutes.
Examples: Pepsi is sweeter than Coke, Brand
Name batteries last longer than "generic" batteries.
13.1 Market Structure
Degree of
Product
Differentiation
Firms produce
identical
products
Firms produce
differentiated
products
Many
Perfect
Competition
Few
One
Dominant
Oligopoly with Dominant
homogeneous firm
products
Monopolistic Oligopoly with
Competition differentiated
-----------products
One
Monopoly
------------
13.1 Market Structure
A) Perfect Competition
1) Many Firms
2) Homogeneous Products
examples: Lemonade stands, fries
B) Monopolistic Competition
1) Many Firms
2) Differentiated Products
Examples: dry cleaning, socks, burgers
13.1 Market Structure
C) Homogeneous Products Oligopoly
1) Few Firms
2) Homogeneous Products
Examples: Convenience Store, Apples
D) Differentiated Products Oligopoly
1) Few Firms
2) Differentiated Products
Examples: Cola, Breakfast Cereals
13.1 Market Structure
E) Dominant Firm
1) One Large Firm, many small firms
2) Homogeneous Products
Examples: Ketchup, MP3 Players
F) Monopoly
1) One Firm
2) One Product
Examples: Canadian Uranium, Canadian Health
Insurance (government monopoly)
13.1 Measuring Market Structure
1) Four-firm Concentration Ratio (4CR)
-Sum of the top 4 sales revenue (in
percentage terms) in an industry
ie1) Internet: Shaw (50%) and Telus (50%)
4CR = 50%+50%=100%
ie2) French Fries: New York (10%), McDonalds
(7%), Wendy’s (4%), Red Robin (3%)
4CR = 10%+7%+4%+3%=24%
*Note: Values are assumptions
13.1 Measuring Market Structure
2) Herfindahl-Hirschman Index (HHI)
-∑(Market Share)2
ie1) Monopoly: HHI=1002=10,000
ie2) 100 Identical Firms: HHI=100(1)2=100
-HHI ranges from 0 (infinite firms) to 10,000 (one
firm)
*Note that the textbook calculations are
inconsistent for HHI
13.1 Measuring Market Structure
-TYPICALLY:
-Industries closer to perfect competition or
monopolistic competition have low 4CR’s and
HHI’s
-Oligopolies have intermediate 4CR’s and HHI’s
-Industries closer to monopolies and dominant
firms have high 4CR’s and HHI’s
-This is a GENERALIZATION (there are
deviations)
13.1 Measuring Market Structure
13.2 Homogeneous Oligopoly
In perfect competition, each firm can ignore all
other firms.
Oligopoly markets feature COMPETITIVE
INDERDEPENDENCE – firm A’s decisions
affect the profits of other firms.
ex) if Firm A overproduces, price falls and
Firm B’s profits decrease
How does this close interdependence affect firm
behavior?
Cournot Oligopoly
Assumptions
• Firms set outputs (quantities)*
• Homogeneous Products
• Simultaneous
• Non-cooperative
*Definition: In a Cournot game, each firm sets its output
(quantity) taking as given the output level of its competitor(s),
so as to maximize profits.
Price adjusts according to demand.
13
Chapter Thirteen
Simultaneously vs. Non-cooperatively
Definition: Firms act simultaneously if each firm
makes its strategic decision at the same time, without
prior observation of the other firm's decision.
Definition: Firms act non-cooperatively if they set
strategy independently, without colluding with the
other firm in any way
14
Chapter Thirteen
Residual Demand
Definition: The relationship between the price
charged by firm i and the demand firm i faces is firm is
residual demand
In other words, the residual demand of firm i is the
market demand minus the amount of demand
fulfilled by other firms in the market: Q1 = Q – Q2;
firms are QUANTITY TAKERS (v. price takers in Perfect
Competition)
Note: We will initially assume only 2 firms,
a
15
DUOPOLY
Chapter Thirteen
Residual Demand
Price
10 units
Residual Marginal Revenue when q2 = 10
Residual Demand when q2 = 10
MC
Demand
0
q1*
Quantity
Best response to q2 = 10
16
Best Response/Reaction Function
Best ResponseThe point where (residual) marginal revenue equals
marginal cost gives ONE best response of firm i to its
rival's action.
Reaction FunctionThe graph of all possible best responses to rival
actions
17
Chapter Thirteen
Reaction Functions
q2
Reaction Function of Firm 1
q2*
0
•
q1*
Reaction Function of Firm 2
q1
Chapter Thirteen
18
Cournot Equilibrium
Equilibrium: No firm has an incentive to
deviate in equilibrium; each firm is maximizing
profits given its rival's output
Each Firm’s output is a BEST RESPONSE to each
other firm’s output.
19
Chapter Thirteen
Cournot Equilibrium Example
P = 100 - Q1 - Q2
MC = AC = 10
What is firm 1's profit-maximizing output when firm 2
produces 50?
Residual demand: P = (100 - Q1) – 50 = 50 - Q1
TR=PQ= 50Q1 - Q12
MR50 = ∂TR/ ∂Q1 = 50 - 2Q1
Since profit is maximized when MR=MC,
MR50 = MC
50 - 2Q1 = 10
40 = 2Q
20 = Q
20
Chapter Thirteen
Cournot Equilibrium Example
P = 100 - Q1 - Q2
MC = AC = 10
What is the equation of firm 1's reaction function?
Residual demand: P = (100 - Q2) - Q1
TR= PQ1 = 100Q1 - Q2 Q1 - Q12
MRr = ∂TR/ ∂Q1 =100 - Q2 - 2Q1
MRr = MC  100 - Q2 - 2Q1 = 10
Q1r = 45 - Q2/2 firm 1's reaction function
•Similarly, Q2r = 45 - Q1/2
21
Cournot Equilibrium Example
P = 100 - Q1 - Q2
Q1r = 45 - Q2/2
MC = AC = 10
Q2r = 45 - Q1/2
Calculate the Cournot equilibrium.
Q1 = 45 - Q2/2
Q1 = 45 - (45 - Q1/2)/2
Q1* = 30
Q2* = 30
P = 100 - Q1 - Q2 = 100 - 30 - 30 = 40
1* = 2* = TR – TC = (P-MC)Q*
1* = 2* = (40-10)(30) = 900
Chapter Thirteen
22
Cournot Solving Steps
1)
2)
3)
4)
5)
Calculate Residual Demand
Calculate (residual) MR
MR=MC to find reaction functions
Use reaction functions to solve for Q’s
Use Q’s to solve for P
-Remember that Q1+Q2=QM
6) Solve for 
7) Summarize
23
Chapter Thirteen
How do firms achieve Cournot Equilibria?
q2
1) Each firm can calculate Reaction
Functions
2) Firm 2 will never produce over A
3) Knowing this, Firm 1 will never produce
under B
4) Knowing this, Firm 2 will never produce
over C
5) This reasoning continues until point Z
A
•
C
q2*
Z
Reaction Function of Firm 2
0
B
q1*
q1
Chapter Thirteen
24
Cournot vs. Monopoly vs. PC
Since Pcournot > MC, Cournot prices are higher than
perfect competition prices
 Cournot firms have market power
BUT, a Cournot market produces more than a
Monopoly, and at a lower price.
Each firm’s pursuit of individual self-interest does not
typically maximize the industry’s profits.
 Each firm wishes the other would decrease
quantity
Monopoly profits are possible if firms collude
25
(which is illegal)
PC vs. Cournot vs. Monopoly
Consider the following outcomes using our above
example of P=100-Q:
The outcome changes greatly with number of firms.
26
Cournot Equilibrium, Many Firms
P = a-bQ
MC = c
N identical firms
Find Cournot Equilibrium Quantity
Residual demand P = a-b(Q1 + Qother)
TR = PQ
= aQ1-bQ12 – bQotherQ1
MR = ∂TR/ ∂Q
= a-2bQ1 – bQother
Since profit is maximized when MR=MC,
MR = MC
a-2bQ1 – bQother = c
Q1=(a-c)/2b – (1/2)Qother
Since Qother = (N-1) Q1,
Q1=(a-c)/2b – (1/2)[(N-1)Q1] Since Q1=Q*
1
ac
Q* 
(
)
( N  1) b
27
Cournot Equilibrium, Many Firms
P = a-bQ
MC = c
N identical firms
Find Cournot Equilibrium Market Price
Since there are N firms,
N
ac
QM 
(
)
( N  1) b
P  a  bQM
N
ac
P  a b
(
)
( N  1) b
a
N
P

c
( N  1) ( N  1)
28
Cournot Solving Steps Multi-Firm
1) Calculate Residual Demand
2) Calculate (residual) MR
3) MR=MC to find reaction functions
New 3b) Remember that Qother = (N-1) Q1
4) Use reaction functions to solve for Q’s
5) Use Q to solve for P
-Remember that ∑Qi=QM
6) Solve for 
7) Summarize
29
Chapter Thirteen
Outcome comparisons
Given the relationship P=a-bQ and MC=c,
30
Chapter Thirteen
13.2 Bertrand Oligopoly
(Homogeneous Products)
Cournot Oligopoly –Firms compete on QUANTITY
Bertrand Oligopoly –Firms compete on PRICES
-Goods must be homogeneous/identical
-A firm’s residual demand depends on the other
firm’s price:
 Zero demand at prices higher than the other
firm
 Market demand at prices lower than the other
firm
Bertrand Oligopoly (homogeneous)
Assumptions:
• Firms set price*
• Homogeneous product
• Simultaneous
• Non-cooperative
*Definition: In a Bertrand oligopoly,
each firm sets its price, taking as
given the price(s) set by other firm(s),
so as to maximize profits.
32
Residual Demand Curve – Price Setting
Price
Market Demand
P2
•
Firm 1’s Residual
Demand Curve
Quantity
0
33
Chapter Thirteen
13.2 Bertrand Oligopoly
(Homogeneous Products)
 Firm A must undercut firm B’s price to sell
anything
 This will force firm B to undercut Firm A
...
 This will continue until neither firm can
decrease price further, P=MC
 The Perfect Competition Result!
Bertrand Equilibrium Example
P = 100 - QT
MC = AC = 10
What is the Bertrand Equilibrium?
P = MC=10
P = 100 – QT
10 = 100 – QT
90 = QT
∏=TR-TC
∏=(P-MC)Q
∏=(10-10)90 = 0
35
Bertrand vs. Cournot
Cournot – Long-Run Competition (Firms choose
output capacity)
Bertrand – Short-Run Competition (Firms have
excess output)
-----------------------------------------------------------------Cournot – Firms can quickly adjust their price, so
price competition is useless
Bertrand – Firms can only slowly adjust price, so
firms believe a price cut can temporarily
increase profits
Stackelberg Oligopoly
Stackelberg model of oligopoly is a situation in which one
firm acts as a quantity leader, choosing its quantity first, with
all other firms acting as followers.
Call the first mover the “leader” and the second mover the
“follower”.
The second firm is in the same situation as a Cournot firm: it
takes the leader’s output as given and maximizes profits
accordingly, using its residual demand.
The second firm’s behavior can, then, be summarized by a
37
Cournot reaction function.
Stackelberg Leader Choice
The Stackelberg leader knows the follower’s
reaction function, and can use that to choose
its production:
P = 100 - QL - QF
MC = AC = 10
What is the equation of the follower’s reaction function?
Residual demand: P = (100 - QL) - QF
TR= PQF = 100QF - QF QL - QF2
MRFr = ∂TR/ ∂Q1 =100 - QL - 2QF
MRFr = MC  100 - QL - 2QF = 10
QFr = 45 - QL/2 follower’s reaction function
38
Stackelberg Leader Choice
P = 100 - QL - QF
QFr = 45 - QL/2
MC = AC = 10
Calculate the Stackelberg equilibrium.
P = 100 - QL - QF = 100 - QL – (45 - QL/2 )
P = 55 – QL/2
TR= PQL = 55QL – QL2/2
MRL = ∂TR/ ∂QL = 55 – QL
MRL = MC  55 – QL = 10
QL = 45
39
Chapter Thirteen
Stackelberg Leader Choice
P = 100 - QL - QF
QFr = 45 - QL/2
MC = AC = 10
QL = 45
Continue Calculating the Stackelberg equilibrium.
QFr = 45 - QL/2 = 45 - 45/2
QFr = 22.5
P = 100 - QL - QF = 100 - 45 – 22.5 = 32.5
L* = TR – TC = (P-MC)QL* = (32.5-10)45 = 1,012.5
F* = TR – TC = (P-MC)QF* = (32.5-10)22.5 = 506.25
40
Chapter Thirteen
Stackelberg Leader Choice
With a Stackelberg leader, price is $32.50, with the leader
producing 45 units for a profit of $1,012.50 and the
following producing 22.5 units for a profit of $506.25.
Notice that:
1) Price is lower than the Cournot equilibrium
2) Leader profits are higher than the cournot
equilibrium
3) Follower profits are lower than the Cournot
equilibrium
41
 There is an advantage to moving first
Stackelberg Solving Steps
1)
2)
3)
4)
5)
Calculate Leader’s Residual Demand
Calculate Leaders (residual) MR
Leader’s MR=MC to find QL
Use QL to solve for QF
Use Q’s to solve for P
-Remember that QL+QF=QM
1) Solve for ’s
2) Summarize
42
Chapter Thirteen
13.3 Dominant Firm Model
The dominant firm model features:
1) A single company with an overwhelming
market share (a dominant firm), D
2) many small producers (competitive fringe),
each of whom has a small market share, F
The dominant firm faces market demand, and
residual demand that takes into account the
competitive fringe’s supply:
Dominant Firm
The dominant
firm’s residual
demand (DR)
is market
demand minus
competitive
fringe supply
(in terms of Q)
44
Dominant Firm Example
P = 100 - QT
MCD = AC = 10
SF: P =10+QF or QF =P - 10
What is the equation of the Dominant Firm’s Residual
Demand?
QR = QT – QF
QR = 100-P – (P-10)
QR = 110-2P
P = 55-QR/2
45
Dominant Firm Example
P = 100 - QT
MCD = AC = 10
SF: P =10+QF or QF =P - 10
QR = 90-2P (P = 55-QR/2)
Calculate Dominant Firm Quantities and Price
TRDR = PQD = 55QD-QD2/2
MRL = ∂TR/ ∂QL = 55 – QD
MRL = MC  55 – QD = 10
QD = 45
P = 55-QR/2
P = 55-45/2 = 32.5
46
Dominant Firm Example
P = 100 - QT
MCD = AC = 10
SF: P =10+QF or QF =P - 10
QR = 90-2P (P = 55-QR/2)
Calculate and check Competitive Fringe Quantities
SF: P =10+QF
32.5 = 10+QF
QF = 22.5
QT = QD + QF
QT = 45 + 22.5 = 67.5
P = 100 – QT
32.5 = 100 – 67.5 = 32.5
47
Dominant Firm Example
P = 100 - QT
SF: P =10+QF or QF =P - 10
MCD = AC = 10
QR = 90-2P (P = 55-QR/2)
QF = 22.5, QD = 45, P=32.5
Calculate market share and dominant firm profit
D: Market Share = QD/ QT = 45/67.5*100 = 66.6%
F: Market Share = QD/ QT = 22.5/67.5*100 = 33.3%
D* = TR – TC = (P-MC)QD* = (32.5-10)45 = 1,012.5
At a price of $32.50, the dominant firm produces
45 units for a profit of $1,012.50, and fringe
48
firms produce 22.5 total.
Dominant Firm Solving Steps
1)
2)
3)
4)
5)
Calculate Dominant Firm`s Residual Demand
Calculate Dominant Firm`s (residual) MR
Leader’s MR=MC to find QD
Use QD to solve for P
Use P to solve for QF
-Remember that QD+QF=QM
1) Solve for  and Market Share
2) Summarize
49
Chapter Thirteen
Aside: Calculating SF
Recall:
 A competitive firm’s supply comes from its MC
curve
 Identical firms supply can be summed (through q)
Fringe Firm: MC=5+20q, 40 firms
Calculate Fringe Supply
MC=5+20q
q=(P-5)/20
QF=40(P-5)/20
QF=2P-10
50
Growing Fringe:
As the size of the fringe grows, the price, and the
production and profits of the dominant firm
decreases (next slide):
There is therefore an incentive for the dominant
firm to practice limit pricing (illegal in Canada):
Limit Pricing – a strategy whereby the dominant firm
keeps its price below the level that maximizes its
current profit in order to reduce the rate of
expansion by the fringe
51
52