Download Good Vibes: Introduction to Oscillations

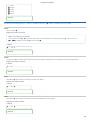
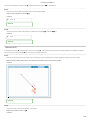
Homework 3 (Chapter 14)
Good Vibes: Introduction to Oscillations
Learning Goal:
To learn the basic terminology and relationships among the main characteristics of simple harmonic motion.
Motion that repeats itself over and over is called periodic motion. There are many examples of periodic motion: the earth revolving around the sun, an
elastic ball bouncing up and down, or a block attached to a spring oscillating back and forth.
The last example differs from the first two, in that it represents a special kind of periodic motion called simple harmonic motion. The conditions that lead to
simple harmonic motion are as follows:
There must be a position of stable equilibrium.
There must be a restoring force acting on the oscillating object. The direction of this force must always point toward the equilibrium, and its
magnitude must be directly proportional to the magnitude of the object's displacement from its equilibrium position. Mathematically, the
restoring force F ⃗ is given by F ⃗ = −kx⃗ , where x⃗ is the displacement from equilibrium and k is a constant that depends on the properties of
the oscillating system.
The resistive forces in the system must be reasonably small.
In this problem, we will introduce some of the basic quantities that describe oscillations and the relationships among them.
Consider a block of mass m attached to a spring with force constant k , as shown in the figure.
The spring can be either stretched or compressed. The block slides on a frictionless horizontal
surface, as shown. When the spring is relaxed, the block is located at x = 0. If the block is
pulled to the right a distance A and then released, A will be the amplitude of the resulting
oscillations.
Assume that the mechanical energy of the block­spring system remains unchanged in the
subsequent motion of the block.
Part A
After the block is released from x
= A
, it will
ANSWER:
remain at rest.
move to the left until it reaches equilibrium and stop there.
move to the left until it reaches x
= −A
and stop there.
move to the left until it reaches x
= −A
and then begin to move to the right.
Correct
As the block begins its motion to the left, it accelerates. Although the restoring force decreases as the block approaches equilibrium, it still pulls
the block to the left, so by the time the equilibrium position is reached, the block has gained some speed. It will, therefore, pass the equilibrium
position and keep moving, compressing the spring. The spring will now be pushing the block to the right, and the block will slow down, temporarily
coming to rest at x = −A.
After x = −A is reached, the block will begin its motion to the right, pushed by the spring. The block will pass the equilibrium position and
continue until it reaches x = A, completing one cycle of motion. The motion will then repeat; if, as we've assumed, there is no friction, the
motion will repeat indefinitely.
The time it takes the block to complete one cycle is called the period. Usually, the period is denoted T and is measured in seconds.
The frequency, denoted f , is the number of cycles that are completed per unit of time: f
Hz ).
= 1/T
. In SI units, f is measured in inverse seconds, or hertz (
Part B
If the period is doubled, the frequency is
ANSWER:
1/25
Homework 3 (Chapter 14)
unchanged.
doubled.
halved.
Correct
Part C
An oscillating object takes 0.10 s to complete one cycle; that is, its period is 0.10 s . What is its frequency f ?
Express your answer in hertz.
ANSWER:
f
= 10 Hz Correct
Part D
If the frequency is 40 Hz, what is the period T ?
Express your answer in seconds.
ANSWER:
T
= 0.025 s Correct
The following questions refer to the figure that graphically depicts the oscillations of the block on
the spring.
Note that the vertical axis represents the x coordinate of the oscillating object, and the horizontal
axis represents time.
Part E
Which points on the x axis are located a distance A from the equilibrium position?
ANSWER:
R only
Q only
both R and Q
Correct
Part F
Suppose that the period is T . Which of the following points on the t axis are separated by the time interval T ?
ANSWER:
2/25
Homework 3 (Chapter 14)
K and L
K and M
K and P
L and N
M and P
Correct
Now assume for the remaining Parts G ­ J, that the x coordinate of point R is 0.12 m and the t coordinate of point K is 0.0050 s .
Part G
What is the period T ?
Express your answer in seconds.
Hint 1. How to approach the problem
In moving from the point t = 0 to the point K, what fraction of a full wavelength is covered? Call that fraction a . Then you can set aT = 0.005 s . Dividing by the fraction a will give the period T .
ANSWER:
T
= 0.02 s Correct
Part H
How much time t does the block take to travel from the point of maximum displacement to the opposite point of maximum displacement?
Express your answer in seconds.
ANSWER:
t
= 0.01 s Correct
Part I
What distance d does the object cover during one period of oscillation?
Express your answer in meters.
ANSWER:
d
= 0.48 m Correct
Part J
What distance d does the object cover between the moments labeled K and N on the graph?
Express your answer in meters.
ANSWER:
d
= 0.36 m Correct
3/25
Homework 3 (Chapter 14)
Harmonic Oscillator Equations
Learning Goal:
To derive the formulas for the major characteristics of motion as functions of time for a horizontal spring oscillator and to practice using the obtained
formulas by answering some basic questions.
A block of mass m is attached to a spring whose spring constant is k . The other end of the spring is fixed so that when the spring is unstretched, the
mass is located at x = 0. . Assume that the +x direction is to the right.
The mass is now pulled to the right a distance A beyond the equilibrium position and released, at
time t = 0 , with zero initial velocity.
Assume that the vertical forces acting on the block balance each other and that the tension of
the spring is, in effect, the only force affecting the motion of the block. Therefore, the system will
undergo simple harmonic motion. For such a system, the equation of motion is
a(t) = −
k
m
x(t) ,
and its solution, which provides the equation for x(t), is
−−
x(t) = A cos(√
k
m
t) .
Part A
At what time t1 does the block come back to its original equilibrium position (x
= 0
) for the first time?
Express your answer in terms of some or all of the variables: A, k , and m.
Hint 1. The cosine function
For the cosine function, cos b
= 0
first when b
= π/2
.
ANSWER:
t1
= π
2√
k
m
Correct
Part B
Find the velocity v of the block as a function of time.
Express your answer in terms of some or all of the variables: k , m, A, and t.
Hint 1. Relationship between x(t) and v(t)
Recall that v(t) =
dx(t)
dt
.
ANSWER:
−−
v(t)
= −√
k
m
−−
Asin(√
k
m
t)
Correct
Part C
What is the maximum speed v max of the block during this motion?
Express your answer in terms of some of all of the variables: k , m, and A.
Hint 1. The sine function
You know that
−−
√
−−
(√
)
4/25
Homework 3 (Chapter 14)
−−
v(t) = −A√
k
m
−−
sin(√
k
m
t) .
What is the maximum value of the sine function?
ANSWER:
v max
= −−
√
k
m
A
Correct
Part D
Find the acceleration a of the block as a function of time.
Express your answer in terms of some of all of the variables: k , m, A, and t.
ANSWER:
−−
a(t)
= −Acos(√
k
m
t)
k
m
Correct
Part E
Specify when the magnitude of the acceleration of the block reaches its maximum value. Consider the following options:
a.
b.
c.
d.
e.
only once during one period of motion,
when the block's speed is zero,
when the block is in the equilibrium position,
when the block's displacement equals either A or −A,
when the block's speed is at a maximum.
Choose the most complete answer.
Hint 1. Extrema of cos(θ)
The function cos(θ) has extrema at θ
= 0, π
.
ANSWER:
a only
b only
c only
d only
e only
b and d
c and e
b and c
a and e
d and e
Correct
Part F
Find the kinetic energy K of the block as a function of time.
Express your answer in terms of some or all of the variables: k , m, A, and t.
Hint 1. Relationship between K(t) and v(t)
Recall that K(t) =
1
2
m(v(t))
2
.
5/25
Homework 3 (Chapter 14)
ANSWER:
K(t)
= −−
0.5m(−Asin(√
k
m
−−
t)√
k
m
2
)
Correct
Part G
Find Kmax , the maximum kinetic energy of the block.
Express your answer in terms of some or all of the variables: k , m, and A.
ANSWER:
Kmax
= 2
0.5A k
Correct
Part H
The kinetic energy of the block reaches its maximum when which of the following occurs?
Hint 1. Extrema of the sine function
The sine function has extrema when its argument equals π/2 , 3π/2 , etc.
ANSWER:
The displacement of the block is zero.
The displacement of the block is A.
The acceleration of the block is at a maximum.
The velocity of the block is zero.
Correct
Exercise 14.13
A frictionless block of mass 2.05 kg is attached to an ideal spring with force constant 280 N/m . At t
and the block is moving in the negative direction at a speed of 12.4 m/s .
= 0
the spring is neither stretched nor compressed
Part A
Find the amplitude.
ANSWER:
A
= 1.06 m Correct
Part B
Find the phase angle.
ANSWER:
ϕ
= 1.57 rad Correct
6/25
Homework 3 (Chapter 14)
Part C
Write an equation for the position as a function of time.
ANSWER:
x = (−
1.06 m )sin(( 11.7 rad/s )t)
x = (−
1.06 m )cos(( 11.7 rad/s )t)
x = (−
11.7 m)sin((1.06 rad/s)t)
x = (−
11.7 m)cos(( 1.06 rad/s)t)
Correct
Energy of Harmonic Oscillators
Learning Goal:
To learn to apply the law of conservation of energy to the analysis of harmonic oscillators.
Systems in simple harmonic motion, or harmonic oscillators, obey the law of conservation of energy just like all other systems do. Using energy
considerations, one can analyze many aspects of motion of the oscillator. Such an analysis can be simplified if one assumes that mechanical energy is
not dissipated. In other words,
E = K + U = constant ,
where E is the total mechanical energy of the system, K is the kinetic energy, and U is the potential energy.
As you know, a common example of a harmonic oscillator is a mass attached to a spring. In this problem, we will consider a horizontally moving block
attached to a spring. Note that, since the gravitational potential energy is not changing in this case, it can be excluded from the calculations.
For such a system, the potential energy is stored in the spring and is given by
U =
1
kx
2
2
,
where k is the force constant of the spring and x is the distance from the equilibrium position.
The kinetic energy of the system is, as always,
K=
1
2
mv
2
,
where m is the mass of the block and v is the speed of the block.
We will also assume that there are no resistive forces; that is, E
= constant
.
Consider a harmonic oscillator at four different moments, labeled A, B, C, and D, as shown in the figure . Assume that the force constant k , the mass of
the block, m, and the amplitude of vibrations, A, are given. Answer the following questions.
Part A
Which moment corresponds to the maximum potential energy of the system?
Hint 1. Consider the position of the block
Recall that U
=
1
2
kx
2
, where x is the distance from equilibrium. Thus, the farther the block is from equilibrium, the greater the potential
energy. When is the block farthest from equilibrium?
ANSWER:
7/25
Homework 3 (Chapter 14)
A
B
C
D
Correct
Part B
Which moment corresponds to the minimum kinetic energy of the system?
Hint 1. How does the velocity change?
Recall that K =
1
2
mv
2
, where v is the speed of the block. When is the speed at a minimum? Keep in mind that speed is the magnitude of
the velocity, so the lowest value that it can take is zero.
ANSWER:
A
B
C
D
Correct
When the block is displaced a distance A from equilibrium, the spring is stretched (or compressed) the most, and the block is momentarily at
rest. Therefore, the maximum potential energy is U max
=
1
2
kA
2
. At that moment, of course, K
= Kmin = 0
. Recall that E
= K +U
.
Therefore,
E=
1
2
kA
2
.
In general, the mechanical energy of a harmonic oscillator equals its potential energy at the maximum or minimum displacement.
Part C
Consider the block in the process of oscillating.
ANSWER:
at the equilibrium position.
at the amplitude displacement.
If the kinetic energy of the block is increasing, the block must be moving to the right.
moving to the left.
moving away from equilibrium.
moving toward equilibrium.
Correct
Part D
Which moment corresponds to the maximum kinetic energy of the system?
Hint 1. Consider the velocity of the block
As the block begins to move away from the amplitude position, it gains speed. As the block approaches equilibrium, the force applied by the
spring—and, therefore, the acceleration of the block—decrease. The speed of the block is at a maximum when the acceleration becomes zero.
At what position does the object begin to slow down?
ANSWER:
8/25
Homework 3 (Chapter 14)
A
B
C
D
Correct
Part E
Which moment corresponds to the minimum potential energy of the system?
Hint 1. Consider the distance from equilibrium
The smallest potential energy corresponds to the smallest distance from equilibrium.
ANSWER:
A
B
C
D
Correct
When the block is at the equilibrium position, the spring is not stretched (or compressed) at all. At that moment, of course, U = Umin = 0.
Meanwhile, the block is at its maximum speed (v max ). The maximum kinetic energy can then be written as K max = mv 2
. Recall that max
1
2
E = K +U
and that U
= 0
at the equilibrium position. Therefore,
E=
1
mv max .
2
2
Recalling what we found out before,
1
E=
2
kA
2
,
we can now conclude that
1
2
kA
2
=
1
2
mv max ,
2
or
−−
v max = √
k
m
A = ωA .
Part F
At which moment is K
= U
?
Hint 1. Consider the potential energy
At this moment, U
=
1
2
U max . Use the formula for Umax to obtain the corresponding distance from equilibrium.
ANSWER:
A
B
C
D
Correct
Part G
Find the kinetic energy K of the block at the moment labeled B.
k
A
9/25
Homework 3 (Chapter 14)
Express your answer in terms of k and A.
Hint 1. How to approach the problem
Find the potential energy first; then use conservation of energy.
Hint 2. Find the potential energy
Find the potential energy U of the block at the moment labeled B.
Express your answer in terms of k and A.
ANSWER:
U
= 1
8
kA
2
ANSWER:
K
= 3
8
k(A)
2
Correct
Exercise 14.27
A toy of mass 0.190­kg is undergoing SHM on the end of a horizontal spring with force constant k = 350 from its equilibrium position, it is observed to have a speed of 0.400 m/s .
N/m
. When the toy is a distance 0.0130 m
Part A
What is the toy's total energy at any point of its motion?
Express your answer with the appropriate units.
ANSWER:
E
= 4.48×10−2 J
Correct
Part B
What is the toy's amplitude of the motion?
Express your answer with the appropriate units.
ANSWER:
A
= 1.60×10−2 m
Correct
Part C
What is the toy's maximum speed during its motion?
Express your answer with the appropriate units.
ANSWER:
v max
= 0.687 m
s
Correct
Exercise 14.31
10/25
Homework 3 (Chapter 14)
A block with mass M attached to a horizontal spring with force constant k is moving with simple harmonic motion having amplitude A1 . At the instant
when the block passes through its equilibrium position, a lump of putty with mass m is dropped vertically onto the block from a very small height and sticks
to it.
Part A
What should be the value of the putty mass m so that the amplitude after the collision is one­half the original amplitude?
Express your answer in terms of the variables M , A1 , and k .
ANSWER:
m
= 3M
Correct
Part B
For this value of m, what fraction of the original mechanical energy is converted into heat?
Express your answer in terms of the variables M , A1 , and k .
ANSWER:
ΔE
E
= 0.750
Correct
Torsional Pendulum
A thin metal disk of mass m = 2.00 × 10 −3 kg and radius R = 2.20 cm is attached at its center to a long fiber. When the disk is turned from the
relaxed state through a small angle θ , the torque exerted by the fiber on the disk is proportional to
θ:
τ = −k θ .
The constant of proportionality k is called the "torsional constant" and is a property of the fiber.
Part A
Find an expression for the torsional constant k in terms of the moment of inertia I of the disk and the angular frequency ω of small, free oscillations.
Express your answer in terms of some or all of the variables I and ω.
Hint 1. Equation of motion
Specify the equation of motion of the problem by using Newton's 2nd law for torques. Equate the angular acceleration of the disk d
2
θ(t)
dt
2
times
its moment of inertia I to the torque τ exerted by the fiber. Neglect all damping effects, such as friction within the fiber or air resistance.
Complete the equation of motion, using θ(t) as the variable.
ANSWER:
I×
d
2
θ(t)
dt
2
= −kθ(t)
11/25
Homework 3 (Chapter 14)
By rearranging the equation of motion, you can bring it into the standard form for a simple harmonic oscillator. This allows you to read off
an expression for the natural frequency of oscillation ω directly. The standard form is
d
2
θ(t)
dt
2
2
+ ω θ(t) = 0 .
ANSWER:
k
= Iω
2
Correct
Part B
The disk, when twisted and released, oscillates with a period T of 1.00 s. Find the torsional constant k of the fiber.
Give your numerical answer for the torsional constant to an accuracy of three significant figures.
Hint 1. Moment of inertia of a disk
What is the moment of inertia I of a uniform disk of radius R and mass m? This is an expression you should know by heart.
ANSWER:
I
= 1
2
mR
2
Hint 2. Angular frequency in terms of the period
Find an expression for the angular frequency of oscillation ω in terms of the period of oscillation T .
You will need the dimensionless constant π.
ANSWER:
ω
= 2π
T
ANSWER:
k
= 1.910×10−5 N ⋅ m/radian Correct
Weighing Lunch
For lunch you and your friends decide to stop at the nearest deli and have a sandwich made fresh for you with 0.300 kg of Italian ham. The slices of ham
are weighed on a plate of mass 0.400 kg placed atop a vertical spring of negligible mass and force constant of 200 N/m . The slices of ham are dropped
on the plate all at the same time from a height of 0.250 m . They make a totally inelastic collision with the plate and set the scale into vertical simple
harmonic motion (SHM). You may assume that the collision time is extremely small.
Part A
What is the amplitude of oscillation A of the scale after the slices of ham land on the plate?
Express your answer numerically in meters and take free­fall acceleration to be g = 9.80 m/s 2 .
Hint 1. How to approach the problem
To find the amplitude of oscillation of the scale you can follow two different methods. First, recall that vertical SHM does not differ substantially
from horizontal SHM, so mathematically one can describe the vertical displacement y of a body oscillating in vertical SHM as a function of time
in the form y(t) = A cos(ωt + ϕ) , where A is the amplitude of oscillation, ω is the angular frequency, and ϕ is the phase angle. If the initial
position y0 and the initial velocity v 0 of the oscillator are given, you can easily calculate the amplitude A. Alternatively, to find A you can
2
apply energy conservation. In fact, in SHM the total mechanical energy is constant and proportional to A . In both cases, however, it will be
necessary to calculate the position and the speed of the plate and the ham immediately after the collision to find the amplitude of oscillation of
the scale.
12/25
Homework 3 (Chapter 14)
Hint 2. Find the position of the plate and the ham immediately after the collision
Once the ham is on the plate, the scale oscillates around a new equilibrium position. How far from the new equilibrium position is the plate when
the slices of ham land on it?
Express your answer for this distance y0 numerically in meters.
Hint 1. New equilibrium position
Before the collision, the plate and the spring are in equilibrium: The weight of the plate balances the elastic force of the spring. After the
collision, because of the added mass of the ham, the plate is no longer in equilibrium and it starts to oscillate around a new equilibrium
position.
Take the position of the plate before the collision as the origin of the vertical coordinate axis and calculate the distance of the new
equilibrium position from the origin by solving a static­equilibrium problem. The new equilibrium position is the point where the combined
weight of the plate and slices of ham balances the elastic force of the spring.
ANSWER:
y0
= 1.47×10−2 m Incorrect; Try Again; 8 attempts remaining
Hint 3. Find the speed of the plate and the ham immediately after the collision
What is the speed v f inal of the plate after the slices of ham land on it?
Express your answer numerically in meters per second.
Hint 1. Use conservation of momentum
Even though there are external forces on the system, the impulse or change in momentum that they produce can be ignored because
the collision time is very small. So we can assume that the momentum of the system, which is purely vertical, is conserved. That is, the
momentum of the ham immediately before the collision equals the momentum of the plate and the ham after the collision.
Hint 2. Find the speed of the ham immediately before the collision
As the slices of ham fall, their potential energy is converted to kinetic energy. When they collide with the plate, their kinetic energy is
equal to the change in potential energy that they experience because of the fall. What is the speed v of the slices of ham immediately
before the collision with the plate?
Express your answer numerically in meters per second.
ANSWER:
v
= 2.21 m/s Hint 3. Find the momentum of the plate and ham after the collision
Consider a slice of ham of mass mh that lands vertically on a plate of mass mp , making a totally inelastic collision with the plate. The
plate is free to move vertically, similarly to the situation described in the introduction of this problem. The speed of the plate and the ham
immediately after the collision is v f inal . What is the momentum pf inal of the plate and the ham immediately after the collision?
ANSWER:
m p v f inal
(m h + m p )v f inal
m h v f inal
(m f inal − m p )v f inal
ANSWER:
v f inal
= 0.949 m/s Incorrect; Try Again; 9 attempts remaining
Hint 4. How to find A by matching initial conditions
Consider an body of mass m in vertical SHM with a force constant k . First note that the angular frequency ω of the body is given by
−−
√
13/25
Homework 3 (Chapter 14)
−−
ω= √
k
.
m
The displacement as a function of time of the body undergoing SHM can be written as
y(t) = A cos(ωt + ϕ)
.
Taking the derivative,we obtain the velocity of the body:
.
, you can solve these two equations to find the constants A and ϕ . In
v(t) = −Aω sin(ωt + ϕ)
If you know the position and velocity of the oscillator at time t
particular,
= 0
−−−−−−−−−−
2
A = √y + (
0
v0
ω
2
)
,
where y0 and v 0 are the initial position and the initial speed of the body, respectively.
Hint 5. Find A using energy conservation
2
The total mechanical energy of the scale at the point of maximum displacement is given by (1/2)kA , where k is the force constant and A is
the amplitude of oscillation. Since the total energy in SHM is constant, then the energy of the scale immediately after the collision must also
2
equal (1/2)kA . What is Etot , the total energy of the system (spring, plate, and ham) immediately after the collision?
Express your answer numerically in joules.
Hint 1. Potential energy in SHM
The potential energy of a body oscillating in SHM is given by (1/2)ky 2 , where k is the force constant and y is the displacement of the
body from equilibrium. It follows that the potential energy of the system (spring, plate, and ham) immediately after the collision depends
on the position of the ham­filled plate with respect to the new equilibrium position.
Hint 2. Kinetic energy
The kinetic energy of the system at a given point in time is given by (1/2)M v 20 , where M is the total mass of the system (mass of the
plate plus mass of the ham) and v 0 is the speed of the plate and the ham at that instant.
ANSWER:
Etot
= 0.337 J Incorrect; Try Again; 7 attempts remaining
ANSWER:
A
= 5.80×10−2 m Correct
Part B
What is the period of oscillation T of the scale?
Express your answer numerically in seconds.
Hint 1. Period of oscillation in SHM
Consider a body of mass m oscillating in simple harmonic motion with a force constant k . The period of oscillation T is given by
−−
T = 2π√
m
k
.
ANSWER:
T
= 0.372 s Correct
Exercise 14.45
14/25
Homework 3 (Chapter 14)
You pull a simple pendulum of length 0.250 m to the side through an angle of 3.50∘ and release it.
Part A
How much time does it take the pendulum bob to reach its highest speed?
Take free fall acceleration to be 9.80 m/s 2 .
ANSWER:
t
= 0.251 s Correct
Part B
How much time does it take if the pendulum is released at an angle of 1.75∘ instead of 3.50∘ ?
ANSWER:
t
= 0.251 s Correct
Exercise 14.52
A small sphere with mass m is attached to a massless rod of length L that is pivoted at the top, forming a simple pendulum. The pendulum is pulled to
one side so that the rod is at an angle θ from the vertical, and released from rest.
Part A
Draw vectors representing the forces acting on the small sphere and the acceleration of the sphere just after it is released. Accuracy counts!
Draw the vectors starting at the sphere. The location and orientation of the vectors will be graded.
ANSWER:
Correct
Part B
At this point, what is the linear acceleration of the sphere?
Express your answer in terms of g , θ
ANSWER:
15/25
Homework 3 (Chapter 14)
a
= gsin(θ)
Correct
Part C
Draw vectors representing the forces acting on the small sphere and the acceleration of the sphere when the pendulum rod is vertical.
Draw the vectors starting at the sphere. The location and orientation of the vectors will be graded.
ANSWER:
Correct
Part D
At this point, what is the linear speed of the sphere?
Express your answer in terms of g , θ , L.
ANSWER:
v
= −−−−−−−−−−−−
√ 2gL(1 − cos(θ))
Correct
Exercise 14.56
A 1.80­kg monkey wrench is pivoted 0.250 m from its center of mass and allowed to swing as a physical pendulum. The period for small­angle oscillations
is 0.940 s .
Part A
What is the moment of inertia of the wrench about an axis through the pivot?
ANSWER:
I
= 9.87×10−2 kg ⋅ m2 Correct
Part B
If the wrench is initially displaced 0.400 rad from its equilibrium position, what is the angular speed of the wrench as it passes through the equilibrium
16/25
Homework 3 (Chapter 14)
position?
ANSWER:
Ω max
= 2.66 rad/s Correct
Exercise 14.61
An unhappy rodent of mass 0.282 kg , moving on the end of a spring with force constant 2.51 N/m , is acted on by a damping force Fx
= −b ⋅ v x
.
Part A
If the constant b has the value 0.898 kg/s , what is the frequency of oscillation of the mouse?
ANSWER:
f
= 0.402 Hz Correct
Part B
For what value of the constant b will the motion be critically damped?
ANSWER:
b
= 1.68 kg/s Correct
Exercise 14.63
A sinusoidally varying driving force is applied to a damped harmonic oscillator of force constant k and mass m. If the damping constant has a value b1 ,
−
−
−
−
the amplitude is A1 when the driving angular frequency equals √ k/m .
Part A
In terms of A1 , what is the amplitude for the same driving frequency and the same driving force amplitude Fmax , if the damping constant is 3b1 ?
Express your answer in terms of the given quantities.
ANSWER:
A
= 1
3
A1
Correct
Part B
In terms of A1 , what is the amplitude for the same driving frequency and the same driving force amplitude Fmax , if the damping constant is b1 /2?
Express your answer in terms of the given quantities.
ANSWER:
A
= 2A 1
Correct
PhET Tutorial: Masses & Springs
17/25
Homework 3 (Chapter 14)
Learning Goal:
To understand how the motion and energetics of a weight attached to a vertical spring depend on the mass, the spring constant, and initial conditions.
For this tutorial, use the PhET simulation Masses & Springs. You can put a weight on the end of a hanging spring, stretch the spring, and watch the
resulting motion.
Start the simulation. When you click the simulation link, you may be asked whether to run, open, or save the file. Choose to run or open it.
You can drag a weight to the bottom of a spring and release it. You can put only one weight on any spring. With the weight on the spring, you can click and
drag the weight up or down and release it. Adjusting the friction slider bar at top right increases or decreases the amount of thermal dissipation (due to air
resistance and heating of the spring). You can adjust the spring constant of spring #3 using the softness spring 3 slider bar. The horizontal dashed line as
well as the ruler can be dragged to any position, which is helpful for comparing positions of the springs.
Feel free to play around with the simulation. When you are done and before starting Part A, set the friction slider bar to the middle and the gravitational
acceleration back to "Earth".
Part A
Place a 50 g weight on spring #1, and release it. Eventually, the weight will come to rest at an equilibrium position, with the spring somewhat stretched
compared to its original (unweighted) length. At this point, the upward force of the spring balances the force of gravity on the weight.
With the weight in its equilibrium position, how does the amount the spring is stretched depend on the mass of the weight?
ANSWER:
The stretch does not depend on mass.
The spring stretches more for a heavier weight.
The spring stretches less for a heavier weight.
Correct
Since the force of gravity on the weight increases as the mass increases, the upward force of the spring must increase for the two forces to
balance (and the weight to therefore be in equilibrium). The force the spring exerts on the weight increases the more the spring is stretched from
its unweighted length.
Part B
Use the simulation to estimate the masses of the three colored, unlabeled weights. Then, place them into the appropriate mass bins.
Hint 1. How to approach the problem
You learned in Part A that a heavier weight stretches the spring more at the equilibrium position. Compare the equilibrium positions for each of
the colored weights to those for the weights with labeled masses. You might want to verify that the three springs all stretch the same amount
for a particular weight, so you can compare the equilibrium positions simultaneously.
ANSWER:
18/25
Homework 3 (Chapter 14)
Correct
Part C
Recall that in the equilibrium position, the upward force of the spring balances the force of gravity on the weight. Use this concept to estimate the
spring constant k of spring #1.
Express your answer in N/m to one significant figure.
Hint 1. How to approach the problem
The spring constant k is used in Hooke’s law for the force exerted by the spring: F = −kx , where x is the amount the spring is stretched.
When the spring is stretched to the equilibrium position, the force exerted by the spring pulling up on the weight is equal to the force of gravity
pulling down. Use this relationship to solve for k .
ANSWER:
k
= 10 N/m Correct
Part D
Now, for parts D­F, you’ll investigate the energetics of the spring.
Select 1 in the Show Energy of box, which shows an energy bar diagram. Select the g = 0 option (under the planet names), which simulates what
happens without any gravitational forces (and consequently removes gravitational potential energy from the energetics). Adjust the friction slider to
none (this prevents any thermal energy from being generated). Place a weight on spring #1, stretch it, and release it. Watch how the kinetic energy
and elastic potential energy vary with time. (You can slow down or stop time using the buttons next to the list of planets.)
When is the elastic potential energy of the spring a maximum?
ANSWER:
When the spring is most compressed
Both when the spring is most compressed and when the spring is most stretched
When the spring is most stretched
When the spring isn’t stretched or compressed
Correct
The elastic potential energy depends on the magnitude of the change in the length of the spring. Mathematically, the elastic potential energy is
given by Uelas = (1/2)kx2 , where k is the spring constant and x is the difference between the length of the spring and its unweighted length. A
compression of x therefore results in the same elastic potential energy as a stretch of x.
19/25
Homework 3 (Chapter 14)
Part E
When is the kinetic energy of the mass a maximum?
ANSWER:
When the spring is most compressed
When the spring is at its unweighted length (when it isn’t stretched or compressed)
When the spring is most stretched
Both when the spring is most compressed and when the spring is most stretched
Correct
The total energy of the system is equal to the kinetic energy of the mass (since the spring has negligible mass) plus the elastic potential energy.
Since this total energy is conserved, the kinetic energy is a maximum when the elastic potential energy is a minimum, which occurs when the
spring is at its unweighted length.
Part F
Select Earth in the menu box so that there is now a force of gravity. Now the total energy of the mass/spring system is the sum of the kinetic energy,
the elastic potential energy, and the gravitational potential energy.
When is the kinetic energy a maximum? (It may help to watch the simulation in slow motion ­ 1/16 time.)
ANSWER:
When the spring is at its unweighted length (its equilibrium position without the weight attached)
When the spring is most stretched or most compressed
When the mass is at the equilibrium position
Correct
The total potential energy (the gravitational potential energy plus elastic potential energy) is a minimum at the equilibrium position, even though
there is some elastic potential energy when the mass is at this location. The kinetic energy is always a maximum when the total potential energy
is a minimum (since the total energy is conserved).
Part G
Now, for parts G­I, you’ll investigate what determines the frequency of oscillation. For these parts, turn off the friction using the slider bar.
Select the stopwatch, and time how long it takes for a weight to oscillate back and forth 10 times. The period of oscillation is this time divided by 10.
The frequency of oscillation is one divided by the period.
How does the frequency of oscillation depend on the mass of the weight?
ANSWER:
The frequency increases as the mass increases.
The frequency decreases as the mass increases.
The frequency is independent of the mass.
Correct
A greater mass results in a lower frequency and a longer period of oscillation.
Part H
The amplitude of oscillation is the maximum distance between the oscillating weight and the equilibrium position. Determine the frequency of
oscillation for several different amplitudes by pulling the weight down different amounts.
How does the frequency depend on the amplitude of oscillation?
ANSWER:
The frequency decreases as the amplitude increases.
The frequency increases as the amplitude increases.
The frequency is independent of the amplitude.
20/25
Homework 3 (Chapter 14)
Correct
Even though the weight has to travel farther each oscillation if the amplitude is greater, the spring on average exerts a stronger force, causing a
greater acceleration and a greater average speed. The effects of the longer distance and faster speed cancel out so that the period of oscillation
doesn’t change!
Part I
The spring constant of spring #3 can be adjusted with the softness spring 3 slider bar (harder means a greater spring constant, or stiffer spring).
How does the frequency of oscillation depend on the spring constant?
Hint 1. How to approach the problem
You can place a weight on spring #3 with the softness of spring 3 set to a very low (soft) value and place another weight with the same mass
on spring #1. Then, release the two weights and compare their frequencies of oscillation.
ANSWER:
The frequency decreases as the spring constant increases.
The frequency is independent of the spring constant.
The frequency increases as the spring constant increases.
Correct
−
−−−−
It turns out that the frequency of oscillation depends on the square root of the ratio of the spring constant to mass: f = √ (k/m) /2π , where f
is the frequency. A stiffer spring constant causes the frequency to increase. Sports cars use stiff springs, whereas large plush Cadillacs use soft
springs for their suspension.
PhET Interactive Simulations
University of Colorado
http://phet.colorado.edu
Video Tutor: Vibrating Rods
First, launch the video below. You will be asked to use your knowledge of physics to predict the outcome of an experiment. Then, close the video window
and answer the question on the right. You can watch the video again at any point.
Part A
Rank the rods shown in the figure in terms of their fundamental resonant frequency, from lowest frequency to highest frequency.
21/25
Homework 3 (Chapter 14)
To rank items as equivalent, overlap them.
Hint 1. How to approach the problem
The resonant frequency depends on the length of the rod.
ANSWER:
Correct
Problem 14.68
A block with mass M rests on a frictionless surface and is connected to a horizontal spring of force constant k . The other end of the spring is attached to
a wall (the figure ). A second block with mass m rests on top of the first block. The coefficient of
static friction between the blocks is μ s .
Part A
Find the maximum amplitude of oscillation such that the top block will not slip on the bottom block.
Express your answer in terms of the variables m, M , k , μ s , and appropriate constants.
ANSWER:
(m+M )gμ
s
k
Correct
Problem 14.72
An object with height h, mass M , and a uniform cross­sectional area A floats upright in a liquid with density ρ .
Part A
Calculate the vertical distance from the surface of the liquid to the bottom of the floating object at equilibrium.
Express your answer in terms of the given quantities.
22/25
Homework 3 (Chapter 14)
ANSWER:
L
= M
Aρ
Correct
Part B
A downward force with magnitude F is applied to the top of the object. At the new equilibrium position, how much farther below the surface of the liquid
is the bottom of the object than it was in part A? (Assume that some of the object remains above the surface of the liquid.)
Express your answer in terms of the given quantities.
ANSWER:
x
= F
Aρg
Correct
Part C
Your result in part B shows that if the force is suddenly removed, the object will oscillate up and down in SHM. Calculate the period of this motion in
terms of the density ρ of the liquid, the mass M , and cross­sectional area A of the object. Neglect the damping due to fluid friction.
Express your answer in terms of the given quantities.
ANSWER:
−
−
−
−
T
= 2π√
M
ρgA
Correct
Problem 14.85
In the figure the upper ball is released from rest, collides with and the stationary lower ball, and
sticks to it. The strings are both 50.0 cm long. The upper ball has mass is 2.00 kg and it is
initially 10.0 cm higher than the lower ball, which has mass 3.00 kg.
Part A
Find the frequency of the motion after the collision.
ANSWER:
f
= 0.705 Hz Correct
Part B
Find the maximum angular displacement of the motion after the collision.
23/25
Homework 3 (Chapter 14)
ANSWER:
θ
= 14.5 ∘ Correct
Problem 14.89
A mass m is attached to a spring of force constant 85.0 N/m and allowed to oscillate. The figure
shows a graph of its velocity v x as a function of time t.
Part A
Find the period.
ANSWER:
T
= 1.60 s Correct
Part B
Find the frequency and the angular frequency of this motion.
Please enter your answers in the order frequency, angular frequency separated with comma.
ANSWER:
f , ω
= 0.625,3.93 Hz ,
rad/s
Correct
Part C
What is the amplitude (in cm)?
ANSWER:
A
= 5.09 cm Correct
Part D
At what times does the mass reach the position x
= ±A
in the interval between t
= 0 s
and t
= 1.8 s
including the endpoints?
If there is more than one value, please enter your answers in ascending order separated with commas.
ANSWER:
t
= 0.400,1.20 s Correct
Part E
24/25
Homework 3 (Chapter 14)
Find the maximum acceleration of the mass.
ANSWER:
|a max |
= 78.5 cm/s 2 Correct
Part F
Find the times at which the maximum acceleration occurs in the interval between t
= 0 s
and t
= 1.8 s
including the endpoints.
If there is more than one value, please enter your answers in ascending order separated with commas.
ANSWER:
t
= 0.400,1.20 s Correct
Part G
What is the mass m?
ANSWER:
m
= 5.51 kg Correct
25/25