Download Lab 7: Conservation of Mechanical Energy

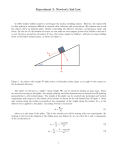
Conservation of Mechanical Energy
Purpose: To verify the conservation of mechanical energy when spring potential energy is
converted to the linear kinetic energy of a cart on an airtrack.
Equipment: Air track and glider, pulley, string, Light spring, Computer, Pphotogate, Mass set
Discussion: The law of conservation of mechanical energy states that if the forces acting on a
system are conservative forces, then the sum of kinetic and potential energies of the system is
constant. A conservative force is one that depends only on the initial and final positions of a body,
and is therefore independent of the path taken. The gravitational force is a conservative force,
whereas the force of friction acting on a body as it moves is an example of a dissipative force,
because it depends on the path taken. In the absence of dissipative forces, the work required to
1
stretch or compress a spring is: Work  PE  k ( x  x0 ) 2
2
where k is the spring constant in N/m, xo is the relaxed position of the spring in meters, and x is the
stretched position. So (x - xo) represents the change in length of the spring in meters. This work is
also the same as the energy (potential energy, PE) stored in the spring, and the work the stretched
spring could do if released. In this lab, we will be converting this stored energy into kinetic energy
(KE) of a glider on an air track, and calculate its velocity using the interface. Assuming there is no
energy loss due to dissipative forces like friction, the potential energy stored in the spring should
then be equal to the kinetic energy of the moving glider. The total mechanical energy of a
conservative system, one with no dissipative forces, remains constant at all times, so that :
PEi + KEi = PEf + KEf
Since the spring has no kinetic energy initially, and the glider had no potential energy as
it travels along the air track at constant velocity, this equation simplifies to:
PEi= KEf or
1
1
k ( x  x0 ) 2  Mv 2
2
2
where “M” is the mass of the glider and “v” is its (constant) velocity after the spring had fully
relaxed. Determine the spring constant as in Lab 1 by plotting spring force(mg) as a function of xx0. The slope is k. The velocity of the glider is simply the distance between the two wooden posts
that are taped to the glider, divided by the time interval between the corresponding two
interruptions seen by the photogate.
Procedure:
1. Check that the air track is level after turning on the blower. The string should be tied around the
two wooden posts securely enough so there can be no slippage. Check that the cardboard support
for the spring is in place and isn't positioned such that it might interfere with a normal relaxing of
the spring when the tension in the string is released.
2. Measure and record the distance "d" between the two wooden posts. Also measure and record the
mass M of the glider.
3. Run the Conservation of Energy App in the UP1 folder. You should see a table of elapsed time.
This is the time for the cart to pass the gate. Record this time in the data table. The distance
between posts divided by the elapsed time is the velocity.
4. You will conduct five trials, beginning with a total of 100 grams hanging, and increasing in 50
grams increments up to a final trial with 300 grams. Each time you stretch the spring to a different
"final position, x", you should record that location to the nearest mm using the yellow scale on the
side of the air track. This data is used to find the spring constant, k.
5. Place your finger on the string vertically down onto the aluminum bracket at the end of the air
track to "freeze" the position of the glider and spring. Then remove the mass from the end of the
string with you free hand, hold the string up and out of the way. Have your partner click "start" and
release the system by quickly removing your finger vertically. This is IMPORTANT: There should
be no tension in the string as the glider passes through the photogate.
6. Prepare the following data table:
Mass of glider: M = __________ kg
Distance between posts d = ___________m
Relaxed position of glider xo = __________ m
Spring constant, k = ______________N/m (From the plot of, F v. stretch.)
note: “xn” is the position for trial “n”.
trial
1
2
3
4
5
xn(m)
xn-x0(m)
md(kg)
md = total hanging mass.
Fspring = weight of hanging mass = mdg
Fspring(N)
t(s)
v(m/s)
Results: report the spring constant and make a table of values for the spring (potential) and glider
(kinetic) and difference as a %, [(KE-PE)/PE]x100.
trial
1
2
3
4
5
PE(J)
KE(J)
%difference
Discuss: Did you expect the % difference to be zero? Why or why not? Is there a trend to the
%difference? If so, describe and explain.
Supplemental Questions: write the questions, show all work, circle the answer.
1. Calculate the velocity of a 50.0g steel ball shot from a slingshot with a 120N/m spring constant
when pulled back 35cm and released.
2. Starting with an unstretched slingshot in #1, follow the work and energy through each
transformation until the steel ball comes to rest after being shot from the slingshot. You should
identify a minimum of four distinct transformations.
3. Keeping other variables the same, what would happen to the velocity of the ball in problem #1 if
the spring constant were doubled?