Download Polynomial functions right- and left

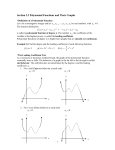
November 10, 2014
Lesson 2.2 Polynomial Functions
For each function:
a.) Graph the function on your calculator
Find an appropriate window.
Draw a sketch of the graph on your paper and
indicate your window.
b.) Identify the degree of the function
c.) Identify the leading coefficient
d.) Describe the
left-hand behavior (what happens to y as x
goes to negative infinity)
and right-hand behavior (what happens to y as
x goes to positive infinity)
1.) y = x3 - x + 1
deg
lead coefficient
left
right
3
2.) y = -2x5 - x2 + 3 5
1
-2
3.) y = - 3x2 + x4 - 1 2
-3
fall
4.) y = -x4 + 2x3
-1
1
fall fall
rise rise
4
4
5.) y = x4 - x2
fall rise
rise fall
fall
How can you determine the left - and right - hand
behavior by examining the equation? Investigate
more polynomial functions on your own if
necessary. Look for patterns.
Polynomial functions right- and left-hand
behavior (end behavior):
Even degree: left- and right- behavior is the same
pos. leading coefficient
rises to left and right
neg. leading coefficient
falls to left and right
pos.
neg
Odd degree: left- and right- behavior is different
pos. leading coefficient
falls to left and rises to right
neg. leading coefficient
rises to left and falls to right
pos.
neg
November 10, 2014
By examining the graph, what can you say about the
degree of the equation and the leading coefficient?
Polynomial Functions
Continuous functions
Domain is the set of all real numbers
Zeros of Polynomial functions
For a polynomial function f of degree n,
1.) f has, at most, n real zeros.
2.) The graph of f has, at most, n-1 relative extrema
(relative minima or maxima)
Ex. The function f(x) = 2x3 -4x+5 has,
at most, 3 real zeroes and
at most, 2 relative extrema
November 10, 2014
For each function below:
a.) Find all real zeros of the function algebraically.
b.) Graph the function on your calculator and
approximate the relative extrema.
1.) f(x) = x3 - x2 - 2x
zeroes: -1, 0, 2
relative extrema: y = .631, y = -2.11
2.) y = -2x4 + 2x2
zeroes: -1, 0, 1
relative extrema: y = .5, 0
Equivalent statements:
x = a is a zero of the function
x = a is an x-intercept of the function
(x - a) is a factor of the polynomial f(x)
(a, 0) is an x-intercept of the graph of f
a is a solution to f(x) = 0
Example:
x = 2 is a zero or x-intercept of the function
(2, 0) is an x-intercept of the function
so (x-2) is a factor of the polynomial
2 is a solution to f(x) = 0
November 10, 2014
1.) The x-intercepts for a function are
(6,0) and (-5,0) and (2,0).
a.) What are the solutions to f(x)=0? 6, -5, 2
b.) What are the zeros of the
function? 6,-5, 2
2.) The zeros of a function are 3 and -2.
a.) State the coordinates of the x-intercepts.
b.) Write an equation for a function with
these zeros.
a) (3,0) (-2,0)
b) y = (x - 3)(x + 2)
y = x2 - x - 6
Find the equation of a quadratic
function with 5 as its only zero.
Sketch the graph.
November 10, 2014
Graph these functions on your calculator.
1.) y = x(x - 2)2(x+4)
2.) y = -.5(x-4)2(x+4)2
3.) y = x2(x - 2)
4.) y = (x-1)3(x+2)2 Use the window -4 < x < 4
-10 < y < 5
Identify the zeroes for each function.
Note whether the graph crosses the x-axis or touches
the x-axis at each zero.
Do you notice a pattern? Describe any pattern you
see.
Sketching the graph of a polynomial
function
Repeated Zeros
For a polynomial function, a factor of (x-a)k , k>1, yields a
repeated zero, x = a of multiplicity k.
(Multiplicity is the power of the factor. The number of
times the factor appears in the product.)
1.) odd multiplicity - the graph crosses the x-axis at a.
2.) even multiplicity, the graph touches the x-axis at a.
Sketch the graph of f(x) = 3x4 - 4x3
November 10, 2014
Sketch the graph of f(x) = 3x4 - 4x3
Finding a polynomial function with
given zeros, multiplicities and
degree.
1.) zero: 2, multiplicity: 1
zero: -3, multiplicity 2
degree: 3
2.) zero: -.5, multiplicity: 1
zero: 0, multiplicity: 2
zero: -4, multiplicity: 3
degree: 6
f(x) = (x-2)(x+3)2
(x-2)(x2+6x+9)
The zero x = -1/2 corresponds to either
x3 + 4x2 - 3x - 18
(x+1/2) or (2x+1) use (2x+1)
f(x) = x2(2x+1)(x+3)3
November 10, 2014
Graph
f(x) = x3 - x2 - 6x
Use your calculator to find the zeroes of
each function.
f(x) = x3 - 4x + 3
f(x) = 2x4 - 6x2 + 5
November 10, 2014
The Intermediate Value Theorem
Let a and b be real numbers such that a < b.
If f is a polynomial function such that f(a) does
not equal f(b),
then, in the interval [a,b], f takes on every
value between f(a) and f(b)
The intermediate value theorem helps you to locate the
real zeros of a polynomial function.
If f(a) is positive and f(b) is negative, you know that the
function has at least one real zero between a and b.
Graph y = 12x3 - 32x2 + 3x + 5
November 10, 2014
Name x-intervals that are I unit long in
which you will find an x-intercept.