Download Phys 345 Electronics for Scientists

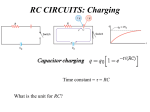
Announcements
• Assignment 1 due now.
• Assignment 2 posted, due on Thursday
Lecture 7 Overview
• Filters
• Transient Circuits
Low pass filter
Vo ( j )
H V ( j ) 
Vi ( j )
Vo ( j ) 
ZC
Vi ( j )
ZC  Z R
1
H V ( j ) 
• RC low-pass filter: preserves lower
frequencies, attenuates frequencies
above the cutoff frequency ω0=1/RC.
1
0 
RC
jC
1
R
jC
1
1
e j0


j tan 1 RC 
2
1
1  jRC
1  (RC ) e
1
 j tan 1 RC

e
2
1  (RC )

1
1  (RC )
2
e
 j tan 1  / 0
Low pass filter
Vo  H V Vi

1
1  (RC ) 2
Vi
o   tan 1  / 0
Break frequency ω=ω0=1/RC,
HV=1/√2
N.B. decibels:
 X 

X dB  20 log 10 
 X0 
 X 

X dB  10 log 10 
X
 0
1
20 log 10
 3db
2
For voltage
For power
Build other filters by combining
impedance response
Which of the following is a low-pass
filter?
What happens to the output voltage when ω→0 (DC condition)?
Answer: (c)
Which of the following are high-pass or
low-pass filters?
Answers: (b) and (c) are highpass; (a) and (d) are low-pass
RLC Band-pass filters
Measuring voltage output
signal over R, Vr
Low frequencies, C open, L
shorted, Vr minimum
High frequency, C shorted, L
open, Vr minimum
so, at high and low
frequencies, see an open
circuit - Vr minimum
C
L
Band-stop (Notch) filters
Measuring voltage output
signal over L and C
Low frequencies, C open, L
shorted, Vlc maximum
High frequency, C shorted, L
open, Vlcmaximum
so, at high and low
frequencies, see an open
circuit - Vlc maximum
Another Example:
Measuring voltage output
signal over L and C, but this
time in parallel (i.e. at high
and low frequencies, see a
short - V0=0)
Transient Circuits
Charging a capacitor
1
1
During Charging (left-hand loop): Integrate both sides using:
dx

 ax  b a ln( ax  b)
  vR (t )  vC (t )  0
dQC
dv
t
iC 
C C
ln(   vC (t ))  
A
Gives:
dt
dt
RC
vR (t )   vc (t )
t
t
iC  iR 



A
R
R
  vC (t )  e e RC  Be RC
dv
  vc (t )
so : C C 
dt
R
Boundary condition: at t=0, vC(t)=0 so:   Be 0  B
dvC
dt
t


  vc (t ) RC
RC
  vc (t )  e t

vC (t )   (1  e RC )
Charging a capacitor
Solution is only true for that particular circuit (Voltage source plus
resistor), but more complicated circuits can be reduced to this using
Thevenin's Theorem
Time constant τ=RC. Time needed to charge capacitor to 63% of full charge
Larger RC means the capacitor takes longer to charge
Larger R implies smaller current flow
The larger C is, the more charge the capacitor can hold.
Discharging a capacitor
Charged
t

RC
Begin discharging
v(t )  e
dq
dv
  RCt
i
C
 e
dt
dt
R
Time constant τ=RC.
Time needed for capacitor to drop to 37% of full charge
Current flows in the opposite direction to charging
Larger RC means the capacitor takes longer to discharge
file:///Users/jholder/teaching/phys645/2011/rc/rc.html
http://www.phy.ntnu.edu.tw/ntnujava/viewtopic.php?t=48
Charging Capacitors
Which configuration has the largest final charge on the capacitor?
Answer: both the same (no current flow means no voltage drop across resistors)
Charging Capacitors
Which capacitor charges fastest?
Answer: b)
Time response of Inductors
Switch to position a:
  VL  iR  0
 L
dI
 iR  0
dt
iL 
di
dt
1
di
dt 
L
  iR

R
, vL  
  iR  L
i

R
(1  e
vL  e


Rt
L
Rt
L
)
)
Integrate and apply boundary condition t=0, i=0
i

R
(1  e

Rt
L
)
Time constant τ=L/R.
Switch to position b:
i

R
e

Rt
L
Talk about "Charging a capacitor"
"Current build-up" in an inductor
Time response of Inductors
A battery is connected to an inductor. When the switch
is opened does the light bulb:
1.Remain off
2.Go off
3. Slowly Dim out
4. Keep burning as brightly as it did before the switch
was opened
5. Flare up brightly, then dim and go out
Answer 5
Why care about Transient Analysis?
not everything is a sine wave....
• Time dependence is very
useful for some applications
(e.g. making a clock)
• Also becomes important in
digital applications
• Transient: refers to transition
region between two states.
• e.g. at the edges of a square
wave
Transient Analysis
Ideal
• Transistors are used as switches in
digital circuits
• Gate input used to control switching
• Physical construction of transistors
leads to "Capacitor Effect"
• Switching is not instantaneous
• Delay determined by RC time
constant
Realistic