Download Polarized Light

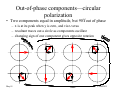
Polarized Light
• Vectors
– what they are and how they apply to light waves
• Linearly polarized light
– Vertical, horizontal, other directions
– Components of linear polarization in other directions
– Law of Malus and linear polarizers
• Circular and elliptical polarization
• Unpolarized light
– Random polarization
• Production of polarized light
• Birefringence and crystals
– waveplates
May 01
LASERS 51
Vectors
• Many physical quantities have both a strength (magnitude)
and a direction
– velocity (magnitude is speed), force, electric field
• Objects with a strength and direction are called vectors
– symbolized by an arrow with length of arrow indicating direction
– sometimes location of base of arrow is significant (where a force is
applied) other times only the strength and direction are important
Force applied
by
support
velocity
May 01
Force of gravity
LASERS 51
Addition (or superposition) of vectors
• More than one vector of the same type can act on one object
(e.g. several forces)
– In this case, vectors must be added
• Vectors are added by placing the tail of the second vector at
the tip of the first
– result is the vector from the tail of the first to the tip of the second
– same result is obtained if first and second vector are reversed
– vectors to be added called components, sum called resultant
Blue vector
added first
May 01
Resultant
vector
Red vector
added first
LASERS 51
Components of a vector
• The sum of the two forces on the car gives the
resultant force
• The resultant is the component of the force of
gravity along the ramp
– The force from the ramp cancels the force of gravity
perpendicular to the ramp
May 01
LASERS 51
Components in any given direction
• To find a vector’s component in a given direction:
– draw a line in the given direction through the tail of the vector
– drop a perpendicular from the tip of the vector to the line
– the component in the given direction is the vector along the given
direction to the point where the perpendicular intersects
– length of component always less than length of vector
vector
Direction
line
Component of vector
in direction of line
May 01
LASERS 51
Independent vectors
• A vector has no component in a direction perpendicular to
the direction of the vector
• Two vectors which are perpendicular to each other are
called independent
Independent
vectors
vector
direction
Vector has zero component in
this direction
May 01
LASERS 51
Linear polarization
• Light is a transverse wave
– electric field and magnetic field vibrate perpendicular to the
propagation direction ( fields have no component along
propagation direction)
– For a horizontal propagation direction, the electric field can
vibrate in the horizontal plane or the vertical direction
– can vibrate in any other transverse direction also
Electric field for
vertical polarization
May 01
Electric field for
horizontal polarization
LASERS 51
What does this diagram mean?
Electric Field at P
P
• This means that at P there is an electric field
– An electric charge placed at P would experience a force
– The direction of the force is indicated by the arrow
– The strength of the force is indicated by the length of
the arrow
• The diagram says nothing about electric fields at
other points
– There is no field indicated at the tip of the arrow or any
other place along it
May 01
LASERS 51
Properties of linearly polarized light
• Polarization direction is always perpendicular to direction of
propagation
– Any two perpendicular directions may be chosen as fundamental
directions (possibly horizontal and vertical for beams propagating
horizontally)
• Electric field vector oscillates in plane of polarization
– Sometimes we symbolize it by a single arrow or double headed
arrow or a line, but if we follow the change in vector with time it
will go positive and negative
y
y
x
Electric field at peak
for vertical
polarization
May 01
x
Electric field at peak
for horizontal
polarization
LASERS 51
Superposition of polarization vectors
• Since the electric field is a vector, two light
waves traveling in the same direction can be
added by adding their electric field vectors
– This just like what we did in interference,
except there we didn’t talk about the direction
of the field vector only its size and phase
beam 2
horizontal
May 01
beam 1
vertical
Resultant
(at one time and
position)
Just as in interference, the
result of adding these two
vibrating fields depends
on the phase of their
vibrations
LASERS 51
Superposition of two in-phase, linearly
polarized waves
• Two linearly polarized waves in phase add to give another
linearly polarized wave with a different polarization plane
– New plane is found by vector addition of two components
• A linearly polarized wave can be thought of (and is) a sum
of two other linearly polarized waves
– Can be resolved into any two orthogonal directions
resultant
At peak
May 01
After peak
After going
through zero
Negative peak
LASERS 51
Pass
direction
Law of Malus
m
a
e
b
t
Outpu
m
ea
b
t
u
p
In
• A beam polarized in the pass direction is transmitted
through the linear polarizer
• A beam polarized perpendicular to the pass direction is
not transmitted
• Several different types of linear polarizer will be
discussed later
• The beam exiting from the linear polarizer is
always polarized in the pass direction
May 01
LASERS 51
Law of Malus
Pass
direction
Component along
pass direction
m
a
e
b
t
Inpu
What if the beam is not polarized
either parallel to or perpendicular
to the pass direction?
Θ
Output
polarization
direction
m
a
e
b
t
Outpu
Input
polarization
direction
• The input polarization is resolved into two components,
along and perpendicular to the pass direction
• The component along the pass direction is transmitted,
the perpendicular component is not
Simple trigonometry gives, Pout=Pin*cos2(Θ)
May 01
LASERS 51
Circular polarization
• There are other ways that the electric field can
vibrate in a light wave
– The vibration must be transverse, i.e. perpendicular to
the propagation direction
– Field direction and magnitude must repeat after a
wavelength
• In circular polarization, the electric field maps out
a circular pattern
– Either observe at fixed point or wave frozen in time
Propagation
direction
Path of electric
field vector
May 01
LASERS 51
Out-of-phase components—circular
polarization
• Two components equal in amplitude, but 90° out of phase
– x is at its peak when y is zero, and vice-versa
– resultant traces out a circle as components oscillate
– changing sign of one component gives opposite rotation
May 01
LASERS 51
Elliptical polarization
• If the x and y components are not equal amplitude, the
path of the resultant is an ellipse
etc.
• If the amplitudes are equal, but the phase difference is not
90° the polarization is also elliptical
x component is
at maximum,
but y is not zero
May 01
LASERS 51
Change of polarization with phase
between x and y components
• Many polarizations can be obtained from the same x
and y components just by changing phase between them
max. y
field
– all possible polarizations can be inscribed in a rectangle
max.
x
field
Phase = 0°
May 01
Phase = 45°
Phase = 90°
Phase = 180°
LASERS 51
Unpolarized (natural) light
• Polarized light is predictable
– If you know light is circularly polarized you know what its electric
field vector will be at any time or place
– The phase difference between the x and y components is fixed
• If the phase between the two components is unpredictable,
rapidly changing in time, the light is unpolarized
– Unpolarized light is a mixture of linearly polarized components in
all possible directions, as well as all possible circular and elliptical
polarizations
– unpolarized light originates in natural (thermal) sources
• Partially polarized light can be thought of as a mixture of
polarized and unpolarized light
– no device exists that can separate the two however
May 01
LASERS 51
Coherent light is always polarized!!!
• If a light wave is perfectly coherent then the x and y
components both have known and constant phases
– Since we know the phase of x and y separately for all time, we
also know their difference
– may be linear, circular, or elliptical, but stays constant
Whoa? What about unpolarized lasers???
• Coherence is an ideal, the phase of a laser eventually (in a
coherence time) “forgets” is past
– coherence time, or coherence length, varies greatly between
different laser types
– during a coherence time polarization of a laser stays constant
– to acknowledge this state of affairs, a laser without a definite
polarization is often called randomly polarized (confusing
terminology, but its all we have for now)
May 01
LASERS 51
Production of polarized light—scattering
scatterers
Single
scaterer
Scattered light,
partially polarized
• Microscopically, light interacts with
materials by setting their electrons in
motion
– the electrons then reradiate producing
absorption, reflection, scattering, and
refractive index
– skylight is partially polarized
May 01
t
n
e
id
c
n
i
-
ed
tter
sca
Incident,
unpolarized light
electron
Force on the electron
is transverse to
propagation direction,
thus only one
polarization emitted
at right angles
LASERS 51
ref
ray lecte
d
Production of polarized light—reflection
nt
ide
inc
ray
• Reflected ray is partially polarized
in the direction out of the paper
air
• Refracted ray is partially polarized
glass
in the plane of the paper
• Reflected ray and refracted ray are
generated by microscopic
radiators also
• When refracted and reflected ray are at 90° the reflected ray
is completely polarized (Brewster’s angle)
• Refracted ray is partially polarized in the plane of the paper
• Reflected ray and refracted ray are generated by
microscopic radiators also
cted
refra
ray
May 01
LASERS 51
Polarization by reflection
• s-polarization
perpendicular to
plane of incidence
1
0.9
0.8
n=1.5
0.7
Reflectivity
both reflectivities
high at grazing
incidence
– from German word
for perpendicular
– sometimes called σ
0.6
0.5
s polarization
0.4
p polarization
both reflectivities
equal at normal
incidence
0.3
0.2
• p-polarization
parallel to plane of
incidence
Brewster's
angle
0.1
0
0
10
20
30
40
50
60
70
80
90
– sometimes called π
Angle (degrees)
Sometimes easiest to remember
as “skip” and “pass”
May 01
LASERS 51
Polarizing pile of plates
• Invented by Arago in 1812
• 15% of s polarization rejected at each surface
– in principle the p-polarization is completely transmitted
– in practice it is difficult to reduce the loss below a few
tenths of a percent
• Still in use for some applications (e.g. CO2 laser at
10.6 µm)
Vertically (p)
Unpolarized
polarized
light
light
May 01
LASERS 51
Polarization by dichroic crystals
• Some natural crystals
(e.g. tourmaline) have
absorption coefficients
that are much larger for
one linear polarization
than another
– electrons are free to
vibrate only along one
axis
– circular dichroic
polarizers also exist
• Polaroid sheet invented by E. Land in 1932
– microscopic polarizing crystals in nitrocellulose sheet
– stretched so all the crystals line up on the same axis
•May “Dichroic”
has other unrelated meanings (its not my LASERS
fault!!)
01
51
Production of polarized light—law of Malus
• What happens when polarized, or unpolarized light is
incident on a linear polarizer?
• Light is
direction of
“resolved” into amplitude of
polarizer
polarization of
transmitted
components
incident light
Θ
light
along and
perpendicular to
Eincident
the polarizer
direction
• Parallel component transmitted, pependicular component
rejected
– transmitted amplitude=Eincident*cosΘ
– transmitted intensity=Iincident*cos2Θ
– holds true even if incident polarization is elliptical or random
May 01
LASERS 51
Production of polarized light by thin
film polarizers
s-polarized
component
Input beam
p-polarized
component
• Glass has a multilayer dielectric coating (similar to
antireflection coating)
• Angle is close to Brewster’s angle (makes coating
design easier)
• All s-polarized light is reflected not just 15%
May 01
LASERS 51
Birefringence (Double refraction)
• Electrons in many crystals have different
forces on them in different directions
– these crystals are said to be anisotropic
– an=not, iso=same, tropic=direction, thus not the
same in every direction
• As a result, the index of refraction depends on
the polarization
– result is refractive index depends on polarization
– Speed of light depends on polarization
May 01
LASERS 51
Optic axis in anisotropic crystals
• In an anisotropic crystal light going in one or two
special directions has the same index of refraction
independent of its polarization
–
–
–
–
these special directions are called the optic axes
optic axis is a direction in the crystal not one particular line
crystals with two optic axes are biaxial
only uniaxial crystals will be discussed here
• Direction of optic axis is closely tied to crystal structure
May 01
LASERS 51
Propagation in a uniaxial crystal
ordinary
polarization
ic
t
• Along optic axis, the light
p
o s
axi
propagates with a single
propagation
refractive index, the
direction
extraordinary
ordinary index, no
polarization
• For other propagation directions, there are two indices
– Resolve the light into two linearly polarized components
• one polarized perpendicular to the optic axis
• one in plane of optic axis and propagation direction
– polarization perpendicular to optic axis has index no
– The other polarization propagates with a different index of
refraction called the extraordinary index, ne
• Extraordinary index depends on the direction of propagation
– Perpendicular to optic axis it differs the most from no
– Smoothly approaches no as direction approaches optic axis
May 01
LASERS 51
Uniaxial crystals—refraction
• Consider a light ray incident at normal
incidence on the surface of a uniaxial
crystal
– A light ray with a polarization
perpendicular to the optic axis is called an
ordinary ray
– A light ray with the other linear polarization
is called an extraordinary ray
ry
a
in
d
or y
ra
ry
a
in
d
r
o
a
r
t
ex y
ra
• At the surface, the ordinary ray obeys Snell’s law, it doesn’t
refract because the incidence angle is zero
– The extraordinary ray bends at the surface (except in the special
case that the optic axis is parallel to the surface)
– At any angle of incidence the ordinary ray obeys Snell’s law
– The extraordinary ray does not in general obey Snell’s law
May 01
LASERS 51
Birefringent polarizers—Nicol prism
• Invented by William Nicol in 1828
– according to Jenkins & White he didn’t understand how it worked
• Start with single crystal of calcite
– cut down ends 3° from natural angle (to 68°)
– cut apart along diagonal
– cement back together with Canada Balsam
• O-ray of calcite has lower index than e-ray, undergoes TIR
at interface, e-ray is transmitted
May 01
LASERS 51
Other birefringent polarizers
• Nicol prisms are simple, but have disadvantages
– relatively small acceptance angle (~28°)
– input is not at normal incidence
– cemented optics cannot be used with high-power lasers or
in the UV
• Several variations exist
– Glan-Thompson is the most popular and overcomes all the
difficulties listed above (but not all at once!)
• Other polarizers separate the two components
– Rochon prism, Wollaston prism
May 01
LASERS 51
Interference of polarized light—waveplates
• Incident polarization is resolved
into o and e polarizations inside
crystal
– shown with optic axis in plane of
plate, but same principles if not
– directions along o and e are called
fast axis and slow axis
direction of
optic axis
Θ
cally
i
t
r
e
ent, v
incid ized beam
polar
• Inside crystal the two waves
propagate independently
– each has its own index and possibly
its own direction
birefringent
plate
t
phase delay of o - ray = not / λ
phase delay of e - ray = net / λ
phase difference = (no − ne )t / λ
Phases given in waves!
• After emerging from crystal, recombine the two waves
using the principle of superposition
– keep track of phase difference in crystal
– continues to propagate in the normal way after exiting crystal
May 01
LASERS 51
Quarter wave plate
• Phase difference is a quarter wave
• If incident light polarized at 45° to
fast axis the o and e components are
equal amplitudes
– emergent light is circularly polarized
• Phase difference is a quarter wave
Slow axis
Fast axis
• If incident light polarized at 45° to fast axis the o and e
components are equal amplitudes
– emergent light is circularly polarized
• If incident light is circularly polarized, output is linearly
polarized
– right-hand circular comes out parallel to fast axis, left to slow
• Other polarizations result in elliptic output, but unpolarized
light comes out unpolarized!
May 01
LASERS 51
Waveplates (cont.)
• Quarter wave plate in which the phase delay is exactly 1/4
λ is called a zero-order plate
– only works exactly for one wavelength (even neglecting
dispersion!!), but close to a quarter wave for other wavelengths
– must be very thin, can be mounted on substrate for structural
stability
– if phase delay is n waves + 1/4 λ acts exactly the same at λ, but
goes out of phase very quickly as λ changes
• Half-wave plate, 90° phase difference
– for linearly polarized input at 45° to fast axis, emergent light is
linearly polarized, but rotated 90°
• Babinet-Soliel compensator, arrangement of birefringent
plates that can produce a variable phase delay
May 01
LASERS 51
Analysis of unknown polarization
• If a linear polarizer is rotated and the transmission goes to
zero at some angle, then input is linearly polarized, DONE.
• If no there is no variation with polarizer rotation, light is
circularly polarized, unpolarized, or a mixture of these
– to distinguish between these, put in λ/4 plate before polarizer
– if light was circular, it will now be linear, detect with polarizer
– if it was unpolarized, it will still be unpolarized, ie no variation
with polarizer
– if there is now a variation with the polarizer but the minima don’t
go to zero, then the light is partially polarized
– degree of polarization defined as
I MAX − I MIN
γ =
I MAX + I MIN
May 01
LASERS 51
Analysis of unknown polarization (cont.)
• If there is a variation with the linear polarizer (and no λ/4
plate) the light must be at least partially polarized but might
also be elliptical
• Insert λ/4 plate with fast axis along direction of maximum
transmission
– for elliptically polarized light, the phase difference between major
and minor axes is also λ/4, but the two components are unequal
amplitude, therefore, the λ/4 plate will convert this to linear
polarization, but an angle to the original maximum, detect with
polarizer
– If the polarizer show that the light is not linear even with the λ/4
plate inserted, the light is not completely polarized, degree of
polarization defined as before, there are still two possibilities
May 01
• if minimum at same angle as before, mixture of linear polarization and
unpolarized, if minimum at different angle then mixture of linear and
elliptical
LASERS 51
Optical rotation
• Some materials exhibit the phenomenon of optical activity– plane polarized light (at any angle) remains plane polarized, but its
angle of polarization rotates as it goes through the material
– Note differences between this behavior and that of a waveplate, in
optical activity: input polarization doesn’t matter, rotation
increases with thickness of the material, output polarization is
always linear
• Optical activity can be induced in some materials due to a
magnetic field, Faraday effect
– This is the only one of the multitude of polarization effects we
have examined which is not reversible
• By reversible I mean that the direction of propagation can be reversed if the
output and input polarizations are switched
– This effect is the basis of optical diodes and optical isolators
May 01
LASERS 51