Download Mechanics: Scalars and Vectors

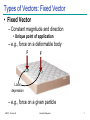
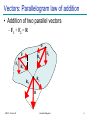
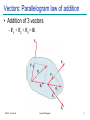
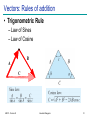
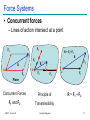
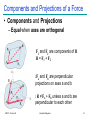
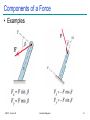
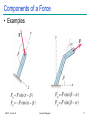
Mechanics: Scalars and Vectors
• Scalar
– Only magnitude is associated with it
• e.g., time, volume, density, speed, energy, mass etc.
• Vector
– Possess direction as well as magnitude
– Parallelogram law of addition (and the triangle
law)
– e.g., displacement, velocity, acceleration etc.
• Tensor
– e.g., stress (33 components)
ME101 - Division III
Kaustubh Dasgupta
1
Mechanics: Scalars and Vectors
A Vector V can be written as: V
= Vn
V = magnitude of V
n = unit vector whose magnitude is one and whose direction
coincides with that of V
Unit vector can be formed by dividing any vector, such as the
geometric position vector, by its length or magnitude
Vectors represented by Bold and Non-Italic letters (V)
Magnitude of vectors represented by Non-Bold, Italic letters
(V)
y
j
x
z
ME101 - Division III
i
k
Kaustubh Dasgupta
2
Types of Vectors: Fixed Vector
• Fixed Vector
– Constant magnitude and direction
• Unique point of application
– e.g., force on a deformable body
F
F
Local
depression
– e.g., force on a given particle
ME101 - Division III
Kaustubh Dasgupta
3
Types of Vectors: Sliding Vector
• Sliding Vector
– Constant magnitude and direction
• Unique line of action
– “Slide” along the line of action
• No unique point of application
Force on
coach F
Force on
coach F
ME101 - Division III
Kaustubh Dasgupta
4
Types of Vectors: Sliding Vector
• Sliding Vector
– Principle of Transmissibility
• Application of force at any point along a particular
line of action
– No change in resultant external effects of the force
ME101 - Division III
Kaustubh Dasgupta
5
Types of Vectors: Free Vector
• Free Vector
– Freely movable in space
• No unique line of action
– No unique point of application
– e.g., moment of a couple
ME101 - Division III
Kaustubh Dasgupta
6
Vectors: Rules of addition
• Parallelogram Law
– Equivalent vector represented by the diagonal
of a parallelogram
• V = V1 + V2 (Vector Sum)
• V  V1 + V2 (Scalar sum)
ME101 - Division III
Kaustubh Dasgupta
7
Vectors: Parallelogram law of addition
• Addition of two parallel vectors
– F1 + F2 = R
-F
F
F1
R2
F2
R1
R1
R2
R
ME101 - Division III
Kaustubh Dasgupta
8
Vectors: Parallelogram law of addition
• Addition of 3 vectors
– F1 + F2 + F3 = R
ME101 - Division III
Kaustubh Dasgupta
9
Vectors: Rules of addition
• Trigonometric Rule
– Law of Sines
– Law of Cosine
B
A
C
ME101 - Division III
Kaustubh Dasgupta
10
Force Systems
Cable
Tension
Force Systems
Cable Tension P
• Force: Represented by vector
– Magnitude, direction, point of application
– P: fixed vector (or sliding vector??)
– External Effect
• Applied force; Forces exerted by bracket, bolts,
Foundation (reactive force)
ME101 - Division III
Kaustubh Dasgupta
12
Force Systems
• Rigid Bodies
– External effects only
• Line of action of force is important
– Not its point of application
– Force as sliding vector
ME101 - Division III
Kaustubh Dasgupta
13
Force Systems
• Concurrent forces
– Lines of action intersect at a point
F2
F2
R = F1+F2
R
F2
A
A
F1
F2
R
R
F1
F1
A
F1
Plane
Concurrent Forces
Principle of
F1 and F2
Transmissibility
ME101 - Division III
Kaustubh Dasgupta
R = F1 + F2
14
Components and Projections of a Force
• Components and Projections
– Equal when axes are orthogonal
F1 and F2 are components of R
R = F1 + F2
:Fa and Fb are perpendicular
projections on axes a and b
: R ≠ Fa + Fb unless a and b are
perpendicular to each other
ME101 - Division III
Kaustubh Dasgupta
15
Components of a Force
• Examples
ME101 - Division III
Kaustubh Dasgupta
16
Components of a Force
• Examples
ME101 - Division III
Kaustubh Dasgupta
17
Components of a Force
Example 1:
Determine the x and y
scalar components of
F1, F2, and F3 acting
at point A of the bracket
ME101 - Division III
Kaustubh Dasgupta
18
Components of Force
Solution:
ME101 - Division III
Kaustubh Dasgupta
19
Components of Force
Alternative Solution: Scalar components of F3 can be
obtained by writing F3 as a magnitude times a unit vector nAB
in the direction of the line segment AB.
Unit vector can be formed by dividing any vector, such as the geometric
position vector by its length or magnitude.
ME101 - Division III
Kaustubh Dasgupta
20
Components of Force
Example 2: The two forces act on a bolt at A. Determine
their resultant.
• Graphical solution –
• Construct a parallelogram with sides in
the same direction as P and Q and
lengths in proportion.
• Graphically evaluate the resultant which
is equivalent in direction and proportional
in magnitude to the diagonal.
• Trigonometric solution
• Use the law of cosines and law of sines
to find the resultant.
ME101 - Division III
Kaustubh Dasgupta
21
Components of Force
Solution:
• Graphical solution - A parallelogram with
sides equal to P and Q is drawn to scale. The
magnitude and direction of the resultant or of
the diagonal to the parallelogram are
measured,
R  98 N   35
• Graphical solution - A triangle is drawn with P
and Q head-to-tail and to scale. The
magnitude and direction of the resultant or of
the third side of the triangle are measured,
R  98 N   35
ME101 - Division III
Kaustubh Dasgupta
22
Components of Force
Trigonometric Solution:
R 2  P 2  Q 2  2 PQ cos B
 40 N 2  60 N 2  240 N 60 N  cos155
R  97.73N
sin A sin B

Q
R
sin A  sin B
Q
R
 sin 155
A  15.04
  20  A
  35.04
ME101 - Division III
Kaustubh Dasgupta
60 N
97.73N
23
Components of Force
Example 3: Tension in cable BC is 725 N; determine the
resultant of the three forces exerted at point B of beam AB.
Solution:
• Resolve each force into
rectangular components.
• Determine the components of the
resultant by adding the
corresponding force components.
• Calculate the magnitude and
direction of the resultant.
ME101 - Division III
Kaustubh Dasgupta
24
Components of Force
Solution
• Resolve each force into rectangular components.
• Calculate the magnitude and direction.
ME101 - Division III
Kaustubh Dasgupta
25
Rectangular Components in Space

• The vector F is
contained in the
plane OBAC.

• Resolve F into
horizontal and vertical
components.
Fy  F cos y
Fh  F sin y
• Resolve Fh into
rectangular
components
Fx  Fh cos 
 F sin  y cos 
Fz  Fh sin 
 F sin  y sin 
ME101 - Division III
Kaustubh Dasgupta
26
Rectangular Components in Space

• With the angles between F and the axes,
Fx  F cos x Fy  F cos y Fz  F cos z




F  Fx i  Fy j  Fz k



 F cos x i  cos y j  cos z k 

 F




  cos x i  cos y j  cos z k


•  is a unit vector along the line of action of F
and cos x , cos y , and cos z are the
direction cosines for F
ME101 - Division III
Kaustubh Dasgupta
27
Rectangular Components in Space
Direction of the force is defined by the location of two points:
M  x1, y1 , z1  and N  x2 , y2 , z 2 

d  vector joining M and N



 d xi  d y j  d z k
d x  x2  x1 d y  y 2  y1 d z  z 2  z1


F  F

 1


  d x i  d y j  d z k 
d
Fd y
Fd x
Fd z
Fx 
Fy 
Fz 
d
d
d
ME101 - Division III
Kaustubh Dasgupta
28