* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Lecture 3
Rotation matrix wikipedia , lookup
Determinant wikipedia , lookup
Euclidean vector wikipedia , lookup
Jordan normal form wikipedia , lookup
Eigenvalues and eigenvectors wikipedia , lookup
Matrix (mathematics) wikipedia , lookup
Singular-value decomposition wikipedia , lookup
Perron–Frobenius theorem wikipedia , lookup
Gaussian elimination wikipedia , lookup
Non-negative matrix factorization wikipedia , lookup
Cayley–Hamilton theorem wikipedia , lookup
Orthogonal matrix wikipedia , lookup
Covariance and contravariance of vectors wikipedia , lookup
Matrix multiplication wikipedia , lookup
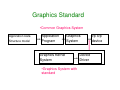
AML710 CAD LECTURE 3 Background Material Revision of Vector Algebra Revision of Matrix Algebra Graphics Standards Coordinate Systems Points and Vectors v = a − b; a, b ∈ E , v ∈ R 3 3 v = (a + w) − (b + w); where w is an arbitrary vector b’ a’ v w w b a v A vertex or point denotes location Whereas a vector has length (magnitude) and direction Barycentric Conditions a+b+c 1 g= = 3 a + 13 b + 13 c 3 v = (a + w) − (b + w); where w is an arbitrary vector c g a b • For vectors both addition and subtraction are defined • Whereas for vertices (points) it results in convex combination • This leads to the definition of convex hull of point sets Revision of Matrix Algebra • Consider the following 2 x 2 matrices A = arc = r1 r2 c1 c2 a11 a21 a12 = a21 a22 • Matrix Addition a11 a11 + b11 A+ B = a21 + b21 a12 a22 ; B = brc = a12 + b12 a22 + b22 b11 b12 b21 b22 Matrix Operations • Multiplication by a scalar quantity kA = ka11 ka12 ka21 ka22 • Matrix multiplication a11 C = AB = a21 a12 b11 b12 a11b11 + a12b21 = a22 b21 b22 a21b11 + a22b21 a11b12 + a12b22 a21b12 + a22b22 • Defined for matrices of r x c, c x r dimensions • This operation is comparable to vector dot product Matrix Operations • Transpose of a matrix – Reflection along leading diagonal A= • Identity matrix a11 a12 a21 a22 A′ = a11 a21 a12 a22 1 0 I= 0 1 AA−1 = A−1 A = I • Every matrix has a transpose. If At=A-1, such a matrix is called orthonormal Graphics Standard •Common Graphics System Application Data Structure model Application Program Graphics System Graphics Kernel System •Graphics System with standard Device Driver I/p o/p device Graphics Standards • GKS an ISO and ANSI standard. Device independent host system independent and application independent • PHIGS – Programmers Hierarchical interactive Graphics System • VDM – Virtual Device Metafile. Defines the function to represent a picture. • VDI – Virtual Device Interface. Lies between GKS and PHIGS • IGES – initial graphics exchange specification. It is an ANSI standard • NAPLPS – North American Presentation Level Protocol Syntax Coordinate Systems • Three types of coordinate systems are generally used in CAD/CAM operations • Model Coordinate System (MCS) or Database CS/ World CS • Working Coordinate System (WCS) • Screen Coordinate System (SCS) or Device CS Model Coordinate System • It is the reference space of the model with respect to which all the model geometrical data is stored. It is a Cartesian system with its X, Y, Z aligned with the characteristics dimension of the model under consideration. The choice of origin is arbitrary. Y H Z P B X D Working Coordinate System • This is basically an auxiliary coordinate system used in place of MCS. For convenience while we develop the geometry by data input this kind of coordinate system is useful. It is very useful when a plane (face) in MCS is not aligned along any orthogonal planes. It is a user defined system that facilitates the geometrical construction. Y X Z H P B D • While user inputs data in WCS the software transforms it to MCS Screen Coordinate System • In contrast to MCS and WCS, Screen Coordinate System is a two-dimensional device-independent system whose origin is usually located at the lower left corner of the display screen. • The SCS is important for display, screen input and digitizing tasks. Y P Z X • For Raster Graphics, the pixel grid serves as the range of SCS. For a 1024x1280, the range is (0,0) to (1024,1280) Digital Image • We know that the SCS is important for display, screen input and digitizing tasks. • A digital image or image on the screen is represented using pixels. • The size of representation depends on the size of the image, the horizontal and the vertical resolution of the screen which are usually indicated as so many pixels per unit length. E.g. dots per inch, pixels per inch etc. Y P Z X