Download Lecture_8


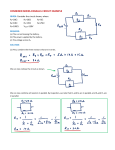
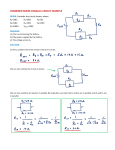
Chapter 25
Electric Currents and
Resistance
Copyright © 2009 Pearson Education, Inc.
Recap
dQ
I
dt
V  IR (Ohm's Law)
2
V
P  IV  I 2 R 
R
Copyright © 2009 Pearson Education, Inc.
25-6 Power in Household Circuits
The wires used in homes to carry electricity
have very low resistance. However, if the current
is high enough, the power will increase and the
wires can become hot enough to start a fire.
To avoid this, we use fuses or circuit breakers,
which disconnect when the current goes above
a predetermined value.
Copyright © 2009 Pearson Education, Inc.
25-6 Power in Household Circuits
Fuses are one-use items – if they blow, the
fuse is destroyed and must be replaced.
 Most common
Common in cars 
Very old type 
Copyright © 2009 Pearson Education, Inc.
25-6 Power in Household Circuits
Circuit breakers, which are now much more
common in homes than they once were, are
switches that will open if the current is too
high; they can then be reset.
Copyright © 2009 Pearson Education, Inc.
25-7 Alternating Current
Current from a battery
flows steadily in one
direction (direct current,
DC). Current from a
power plant varies
sinusoidally (alternating
current, AC).
Copyright © 2009 Pearson Education, Inc.
25-7 Alternating Current
The voltage varies sinusoidally with time:
,,
as does the current:
Copyright © 2009 Pearson Education, Inc.
25-7 Alternating Current
Multiplying the current and the voltage gives
the power:
Copyright © 2009 Pearson Education, Inc.
25-7 Alternating Current
Usually we are interested in the average power:
1
sin  
2
1

2
2

2
0
sin  d    sin  cos 
 
2
0
2

1
1  sin  d 1 
2
2
1
 sin  
2
2
 P  I 2 R  I 02 R sin 2  t
1 2
1 V02
 I0 R 
P
2
2 R
Copyright © 2009 Pearson Education, Inc.

2
0
2
0
1

2

2
0
sin 2  d
cos 2  d
25-7 Alternating Current
The current and voltage both have average
values of zero, so we square them, take the
average, then take the square root, yielding the
root-mean-square (rms) value:
Copyright © 2009 Pearson Education, Inc.
25-7 Alternating Current
Example 25-13: Hair dryer.
(a) Calculate the resistance and the peak current
in a 1000-W hair dryer connected to a 120-V line.
(b) What happens if it is connected to a 240-V line
in Britain?
Copyright © 2009 Pearson Education, Inc.
25-8 Microscopic View of Electric
Current: Current Density and Drift
Velocity
Electrons in a conductor have large, random
speeds just due to their temperature. When a
potential difference is applied, the electrons
also acquire an average drift velocity, which is
generally considerably smaller than the
thermal velocity.
Copyright © 2009 Pearson Education, Inc.
25-8 Microscopic View of Electric
Current: Current Density and Drift
Velocity
We define the current density (current per
unit area) – this is a convenient concept
for relating the microscopic motions of
electrons to the macroscopic current:
If the current is not uniform:
.
Copyright © 2009 Pearson Education, Inc.
25-8 Microscopic View of Electric
Current: Current Density and Drift
Velocity
This drift speed is related to the current in the
wire, and also to the number of electrons per unit
volume:
and
Copyright © 2009 Pearson Education, Inc.
25-8 Microscopic View of Electric
Current: Current Density and Drift
Velocity
Example 25-14: Electron speeds in a wire.
A copper wire 3.2 mm in diameter carries a 5.0A current. Determine (a) the current density in
the wire, and (b) the drift velocity of the free
electrons. (c) Estimate the rms speed of
electrons assuming they behave like an ideal
gas at 20°C. Assume that one electron per Cu
atom is free to move (the others remain bound
to the atom).
Copyright © 2009 Pearson Education, Inc.
25-8 Microscopic View of Electric
Current: Current Density and Drift
Velocity
The electric field inside a current-carrying
wire can be found from the relationship
between the current, voltage, and resistance.
Writing R = ρ l/A, I = jA, and V = El , and
substituting in Ohm’s law gives:
Copyright © 2009 Pearson Education, Inc.
25-8 Microscopic View of Electric
Current: Current Density and Drift
Velocity
Example 25-15: Electric field inside a wire.
What is the electric field inside the wire of
Example 25–14? (The current density was
found to be 6.2 x 105 A/m2.)

E   j  1.68  108
Copyright © 2009 Pearson Education, Inc.


6.2  105  0.01 V m
25-9 Superconductivity
In general, resistivity
decreases as
temperature decreases.
Some materials,
however, have
resistivity that falls
abruptly to zero at a
very low temperature,
called the critical
temperature, TC.
Copyright © 2009 Pearson Education, Inc.
25-9 Superconductivity
Experiments have shown that currents, once
started, can flow through these materials for
years without decreasing even without a
potential difference.
Critical temperatures are low; for many years no
material was found to be superconducting above
23 K.
Since 1987, new materials have been found that
are superconducting below 90 K, and work on
higher temperature superconductors is
continuing.
Copyright © 2009 Pearson Education, Inc.
Summary of Chapter 25
• A battery is a source of constant potential
difference.
• Electric current is the rate of flow of electric
charge.
• Conventional current is in the direction that
positive charge would flow.
• Resistance is the ratio of voltage to current:
Copyright © 2009 Pearson Education, Inc.
Summary of Chapter 25
• Ohmic materials have constant resistance,
independent of voltage.
• Resistance is determined by shape and
material:
• ρ is the resistivity.
Copyright © 2009 Pearson Education, Inc.
Summary of Chapter 25
• Power in an electric circuit:
• Direct current is constant.
• Alternating current varies sinusoidally:
Copyright © 2009 Pearson Education, Inc.
Summary of Chapter 25
• The average (rms) current and voltage:
• Relation between drift speed and current:
Copyright © 2009 Pearson Education, Inc.
Chapter 26
DC Circuits
Copyright © 2009 Pearson Education, Inc.
Units of Chapter 26
• EMF and Terminal Voltage
• Resistors in Series and in Parallel
• Kirchhoff’s Rules
• Series and Parallel EMFs; Battery Charging
• Circuits Containing Resistor and Capacitor
(RC Circuits)
•Ammeters and Voltmeters
Copyright © 2009 Pearson Education, Inc.
26-2 Resistors in Series and in
Parallel
A series connection has a single path from
the battery, through each circuit element in
turn, then back to the battery.
Series = absolutely, positively, no-question-about-it same current through resistors!
Copyright © 2009 Pearson Education, Inc.
26-2 Resistors in Series and in
Parallel
The current through each resistor is the
same; the voltage depends on the
resistance. The sum of the voltage
drops across the resistors equals the
battery voltage:
V  V1  V2  V3 
 IR1  IR2  IR3 
 I  R1  R2  R3 
 Req = R1  R2  R3 
Copyright © 2009 Pearson Education, Inc.

[Series]
26-2 Resistors in Series and in
Parallel
From this we get the equivalent resistance (that
single resistance that gives the same current in
the circuit):

Copyright © 2009 Pearson Education, Inc.
26-1 EMF and Terminal Voltage
Electric circuit needs battery or generator to
produce current – these are called sources of
emf (archaic term: electromotive force).
Battery is a nearly constant voltage source, but
does have a small internal resistance, which
reduces the actual voltage from the ideal emf:
Copyright © 2009 Pearson Education, Inc.
26-1 EMF and Terminal Voltage
This resistance behaves as though it were in
series with the emf.
Copyright © 2009 Pearson Education, Inc.
26-1 EMF and Terminal Voltage
Example 26-1: Battery with internal resistance.
A 65.0-Ω resistor is
connected to the
terminals of a battery
whose emf is 12.0 V and
whose internal
resistance is 0.5 Ω.
Calculate (a) the current
in the circuit, (b) the
terminal voltage of the
battery, Vab, and (c) the
power dissipated in the
resistor R and in the
battery’s internal resistance r.
Copyright © 2009 Pearson Education, Inc.
ConcepTest 26.1b
Series Resistors II
1) 12 V
In the circuit below, what is the
2) zero
voltage across R1?
3) 6 V
4) 8 V
5) 4 V
R1 = 4 W
R2 = 2 W
12 V
ConcepTest 26.1b
Series Resistors II
1) 12 V
In the circuit below, what is the
2) zero
voltage across R1?
3) 6 V
4) 8 V
5) 4 V
The voltage drop across R1 has
to be twice as big as the drop
across R2. This means that V1 =
R1 = 4 W
R2 = 2 W
8 V and V2 = 4 V. Or else you
could find the current I = V/R =
(12 V)/(6 W = 2 A, and then use
Ohm’s law to get voltages.
12 V
26-2 Resistors in Series and in
Parallel
A parallel connection splits the current; the
voltage across each resistor is the same:
Parallel = absolutely, positively, no-question-about-it same potential drop across resistors!
Copyright © 2009 Pearson Education, Inc.
26-2 Resistors in Series and in
Parallel
The total current is the sum of the currents
across each resistor:
I  I1  I 2  I 2 
V
V V V





Req R1 R2 R3
 1
1
1
V 



 R1 R2 R3
1
1
1
1





Req R1 R2 R3
Copyright © 2009 Pearson Education, Inc.



[Parallel]
26-2 Resistors in Series and in
Parallel
An analogy using water
may be helpful in
visualizing parallel
circuits. The water
(current) splits into two
streams; each falls the
same height, and the total
current is the sum of the
two currents. With two
pipes open, the resistance
to water flow is half what
it is with one pipe open.
Copyright © 2009 Pearson Education, Inc.
26-2 Resistors in Series and in
Parallel
Conceptual Example 26-2: Series or parallel?
(a) The lightbulbs in the figure are identical.
Which configuration produces more light? (b)
Which way do you think the headlights of a car
are wired? Ignore change of filament resistance R
with current.
Copyright © 2009 Pearson Education, Inc.
ConcepTest 26.2b
Points P and Q are connected to a
Parallel Resistors II
1) increases
battery of fixed voltage. As more
2) remains the same
resistors R are added to the parallel
3) decreases
circuit, what happens to the total
4) drops to zero
current in the circuit?
ConcepTest 26.2b
Parallel Resistors II
Points P and Q are connected to a
1) increases
battery of fixed voltage. As more
2) remains the same
resistors R are added to the parallel
3) decreases
circuit, what happens to the total
4) drops to zero
current in the circuit?
As we add parallel resistors, the overall
resistance of the circuit drops. Since V =
IR, and V is held constant by the battery,
when resistance decreases, the current
must increase.
Follow-up: What happens to the current through each resistor?
26-2 Resistors in Series and in
Parallel
Conceptual Example 26-3: An illuminating surprise.
A 100-W, 120-V lightbulb and a 60-W, 120-V lightbulb
are connected in two different ways as shown. In each
case, which bulb glows more brightly? Ignore change
of filament resistance with current (and temperature).
Copyright © 2009 Pearson Education, Inc.
26-2 Resistors in Series and in
Parallel
Example:
What is the current through each resistor shown?
Copyright © 2009 Pearson Education, Inc.
26-2 Resistors in Series and in
Parallel
Conceptual Example 26-6:
Bulb brightness in a circuit.
The circuit shown has
three identical lightbulbs,
each of resistance R.
(a) When switch S is
closed, how will the
brightness of bulbs
A and B compare with
that of bulb C? (b) What
happens when switch S is
opened? Use a minimum of
mathematics in your answers.
Copyright © 2009 Pearson Education, Inc.
26-2 Resistors in Series and Parallel
Example 26-8:
Analyzing a circuit.

A 9.0-V battery whose
internal resistance r is
0.50 Ω is connected in
the circuit shown. (a)
How much current is

drawn from the
battery? (b) What is
the terminal voltage of
the battery? (c) What
is the current in the
6.0-Ω resistor?
Copyright © 2009 Pearson Education, Inc.


















Multiple configurations
Assume that in each
circuit the battery gives
12 V and each resistor
has a resistance of 4
ohms. In which circuit
does the largest current
flow through the
battery? What is that
current?
Copyright © 2009 Pearson Education, Inc.
Multiple configurations
Assume that in each
circuit the battery gives
12 V and each resistor
has a resistance of 4
ohms. In which circuit
does the largest current
flow through the
battery? What is that
current?
1
1 1 2
  
R12 R R R
 R12  R 2
 R123  R12  R 
Copyright © 2009 Pearson Education, Inc.
3R
V
2V 2 12
I


2A
2
R123 3 R 3 4
Circuit Maze
If each resistor has a
resistance of 4 W and
each battery is a 4 V
battery, what is the
current flowing
through the resistor
labelled “R”?
Copyright © 2009 Pearson Education, Inc.
Circuit Maze
If each resistor has a
resistance of 4 W and
each battery is a 4 V
battery, what is the
current flowing
through the resistor
labelled “R”?
I
V 8
 2A
R 4
Copyright © 2009 Pearson Education, Inc.
__________________________
|
|
|
12 |
|
12 |
|
|
__ |
|
____
| ____|
||
8 ||
8|
|
|
0
___|
|
|
||
4|
|
|
|
|
|
|
|
|
0  _______________________
26-3 Kirchhoff’s Rules
Some circuits cannot be broken down into
series and parallel connections. For these
circuits we use Kirchhoff’s rules.
Copyright © 2009 Pearson Education, Inc.
26-3 Kirchhoff’s Rules
Junction rule: The sum of currents entering a
junction equals the sum of the currents
leaving it (i.e., charge does not pile up).
Copyright © 2009 Pearson Education, Inc.
26-3 Kirchhoff’s Rules
Loop rule: The sum of
the changes in
potential around a
closed loop is zero.
Copyright © 2009 Pearson Education, Inc.
26-3 Kirchhoff’s Rules
Problem Solving: Kirchhoff’s Rules
1. Label each current, including its direction.
2. Identify unknowns.
3. Apply junction and loop rules; you will
need as many independent equations as
there are unknowns. Each new equation
MUST include a new variable.
4. Solve the equations, being careful with
signs. If the solution for a current is
negative, that current is in the opposite
direction from the one you have chosen.
Copyright © 2009 Pearson Education, Inc.
26-3 Kirchhoff’s Rules
Example: Using Kirchhoff’s rules.
a) Calculate the currents (call them I1, I2, and
I3) through the three batteries of the circuit
in the figure.
b) What is Va-Vb?
1  2.0 V
 2   3  4.0 V
R1  1.0 W
R2  2.0 W
Copyright © 2009 Pearson Education, Inc.
ConcepTest 26.12
More Kirchhoff’s Rules
1) 2 – I1 – 2I2 = 0
Which of the equations is valid
2) 2 – 2I1 – 2I2 – 4I3 = 0
for the circuit below?
3) 2 – I1 – 4 – 2I2 = 0
4) I3 – 4 – 2I2 + 6 = 0
5) 2 – I1 – 3I3 – 6 = 0
1W
I2
2W
6V
22 VV
4V
I1
1W
I3
3W
ConcepTest 26.12
More Kirchhoff’s Rules
1) 2 – I1 – 2I2 = 0
Which of the equations is valid
2) 2 – 2I1 – 2I2 – 4I3 = 0
for the circuit below?
3) 2 – I1 – 4 – 2I2 = 0
4) I3 – 4 – 2I2 + 6 = 0
5) 2 – I1 – 3I3 – 6 = 0
Eq. 3 is valid for the left loop:
The left battery gives +2 V, then
there is a drop through a 1 W
resistor with current I1 flowing.
Then we go through the middle
battery (but from + to – !), which
gives –4 V. Finally, there is a
drop through a 2 W resistor with
current I2.
1W
I2
2W
6V
22 VV
4V
I1
1W
I3
3W
Questions?
Copyright © 2009 Pearson Education, Inc.