* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download General Principles of Tomography
Survey
Document related concepts
Transcript
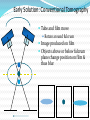
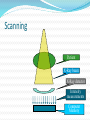
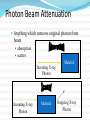
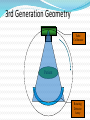
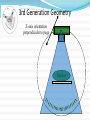
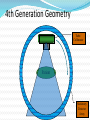
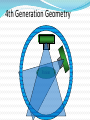
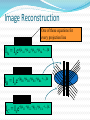
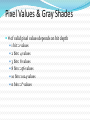
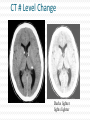
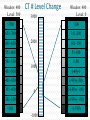
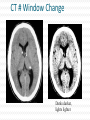
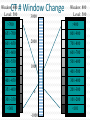
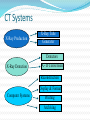
CT Chapter 4: Principles of Computed Tomography Radiography vs. CT Both based on differential attenuation of x-rays passing through body Radiography “Shadowgraph” using x-ray light source CT Cross-sectional image Image computed from pencil beam intensity measurements through only slice of interest Limitations of Radiography 3D body rendered in 2D Structures superimposed on film Must view structure of interest through underlying / overlying structures Multiple views often required to adequately visualize a structure. X-ray Beam Patient Film Limitations of Radiography Optical density dictated by total attenuation encountered by beam Thin dense object Thin highly-attenuating objects appear to be same density as thicker lowattenuating object. X-ray Beam Patient Thick less dense object Film Early Solution: Conventional Tomography Tube and film move Rotate around fulcrum Image produced on film Objects above or below fulcrum plane change position on film & thus blur Limitations of Conventional Tomography Overlying / underlying structures blurred, not removed 5-10% subject contrast difference required for objects to appear different many anatomic systems do not have this subject contrast CT Advantages View anatomy without looking through underlying / overlying structures improves contrast Conventional X-ray Beam Uses tightly collimated beam minimizes scattered radiation improves contrast Demonstrates very small contrast differences reliable & repeatedly CT X-ray Beam Film as a Radiation Detector Analog not quantitative Not sensitive enough to distinguish small differences in incident radiation Applications film badges therapy dosimetry CT Detectors electronic / quantitative extremely sensitive small radiation input differences reliably & repeatedly measured & discerned output digitized & sent to computer Data Aquisition Slice by slice One slice at a time Volume acquisition data for an entire volume collected patient moves in axial direction during scan tube traces spiral-helical path through patient Scanning X-ray tube rotates around patient detectors also rotate for 3rd generation CT Detectors measure radiation Patient transmitted through patient for various pencil beam projections Relative transmissions calculated Fraction of beam exiting patient X-Ray beams Scanning Patient X-Ray beam X-Ray detector Intensity measurements Computer Memory Photon Phate What can happen to an x-ray photon passing through a material (tissue)? Incoming X-ray Photon Material ??? Photon Phate #1: Nothing Photon exits unaffected same energy same direction Incoming X-ray Photon Material Outgoing X-ray Photon Photon Phate #2: Absorption Photon disappears Its energy is absorbed by material Incoming X-ray Photon Material Photon Phate #3: Scatter Lower energy photon emerges energy difference deposited in material Photon usually emerges in different direction Incoming X-ray Photon Material Outgoing X-ray Photon Photon Beam Attenuation Anything which removes original photon from beam absorption scatter Incoming X-ray Photon Incoming X-ray Photon Material Material Outgoing X-ray Photon Example Beam Attenuation (Mono-energy source) Each cm of material reduces beam intensity 20% exiting beam intensity 80% of incident for 1 cm absorber 1cm 100 1cm 100 * .8 = 80 1cm 80 * .8 = 64 1cm 64 * .8 = 51 51 * .8 = 41 Attenuation Equation for Mono-energetic Photon Beams I = Io -mx e I = Exiting beam intensity Io = Incident beam intensity e = constant (2.718…) m = linear attenuation coefficient •property of •absorber material •beam energy x = absorber thickness For photons which are neither absorbed nor scattered Material Io x I Example Beam Attenuation Using equation to calculate beam intensity for various absorber thicknesses (m = .223) I = Ioe-mx 100 1cm 80 -20% 100*e-(0.223)(1) = 80 Example Beam Attenuation Using equation to calculate beam intensity for various absorber thicknesses (m = .223) I = Ioe-mx 100 1cm -20% 80 1cm 64 -20% 100*e-(0.223)(2) = 64 Example Beam Attenuation Using equation to calculate beam intensity for various absorber thicknesses (m = .223) I = Ioe-mx 100 1cm -20% 80 1cm -20% 64 1cm -20% 100*e-(0.223)(3) = 51 51 Example Beam Attenuation Using equation to calculate beam intensity for various absorber thicknesses (m = .223) I = Ioe-mx 100 1cm -20% 80 1cm -20% 64 1cm 51 -20% 100*e-(0.223)(4) = 41 1cm 41 -20% More Realistic CT Example Beam Attenuation for non-uniform Material 4 different materials 4 different attenuation coefficients x #1 #2 #3 #4 Io I m1 m2 m3 m4 I = Io -(m +m +m +m )x 1 2 3 4 e Effect of Beam Energy on Attenuation Low energy photons more easily absorbed High energy photons more penetrating All materials attenuate a larger fraction of low than high energy photons Material 100 Higher-energy mono-energetic beam 80 100 Material Lower-energy mono-energetic beam 30 Mono vs. Poly-energetic X-ray Beam Equations below assume Mono-energetic x-ray beam x #1 #2 #3 #4 Io I m1 m2 m3 m4 I = Io -mx e I = Io -(m +m +m +m )x 1 2 3 4 e Mono-energetic X-ray Beams Available from radionuclide sources Not used in CT because beam intensity much lower than that of an x-ray tube X-ray Tube Beam High intensity Produces poly-energetic beam x #1 #2 #3 #4 Io I m1 m2 m3 m4 I = Io -(m +m +m +m )x 1 2 3 4 e Beam Hardening Complication Attenuation coefficients mn depend on beam energy!!! Beam energy incident on each block unknown Four m’s, each for a different & unknown energy 1cm 1cm 1cm 1cm m1 m2 m3 m4 I = Io -(m +m +m +m )x 1 2 3 4 e Beam Hardening Complication Beam quality changes as it travels through absorber greater fraction of low-energy photons removed from beam Average beam energy increases A 1cm B Fewer Photons But higher avg kV than A 1cm C 1cm Fewer Photons But higher avg kV than B D 1cm Fewer Photons But higher avg kV than C E Fewer Photons But higher avg kV than D Your Job: Stop People at the Gate Set up multiple gates, one behind the other Catch as many as you can at first gate Catch as many as you can who got through gate #1 at gate #2 Monitor average weight of crowd getting through each gate Reconstruction Scanner measures “I” for thousands of pencil beam projections Computer calculates tens of thousands of attenuation coefficients one for each pixel Computer must correct for beam hardening effect of increase in average beam energy from one side of projection to other I = Io -(m +m +m +m +...)x 1 2 3 4 e Data Acquisition Geometries All CT generations obtain same set of multi- line transmission measurements in many directions Generational differences Protocol for obtaining line transmissions geometry / location of tube / detector motion # of line transmissions obtained simultaneously speed Why is CT done with High kV’s? Less dependence of attenuation coefficient on photon energy Attenuation coefficient changes less at higher kV’s Reduce contrast of bone relative to soft tissue Produce high radiation flux at detector Common Data-Acquisition Geometries Tube rotates around patient Detector system Rotates with x-ray tube (3rd generation) Stationary (4th generation) 360o ring of detectors 3rd Generation Geometry Tube / Collimator Patient Rotating Detector Array 3rd Generation Geometry Z-axis orientation perpendicular to page Patient 4th Generation Geometry Tube / Collimator Patient Stationary Detector Array 4th Generation Geometry Patient Image Reconstruction Projection #A One of these equations for every projection line IA = Ioe-(mA1+mA2+mA3+mA4 +...)x Projection #B IB = Ioe-(mB1+mB2+mB3+mB4 +...)x Projection #C IC = Ioe-(mC1+mC2+mC3+mC4 +...)x Image Reconstruction * Projection #A What We Measure: IA, IB, IC, ... IA = Ioe-(mA1+mA2+mA3+mA4 +...)x Projection #B IB = Ioe-(mB1+mB2+mB3+mB4 +...)x Projection #C IC = Ioe-(mC1+mC2+mC3+mC4 +...)x Reconstruction Calculates: mA1, mA2, mA3, ... mB1, mB2, mB3, ... mC1, mC2, mC3, ... Etc. CT Number Calculated from reconstructed pixel attenuation coefficient (mt - mW) CT # = 1000 X -----------mW Where: ut = linear attenuation coefficient for tissue in pixel uW = linear attenuation coefficient for water CT Numbers for Special Stuff Bone: +1000 Water: 0 Air: -1000 (mt - mW) CT # = 1000 X -----------mW Display & Windowing Gray shade assigned to each pixel value (CT #) Windowing 47 93 Assignment of display brightness to pixel values does not disturb original pixel values in memory Operator controllable window level Display & Display Matrix: Resolution CT images usually 512 X 512 pixels Display resolution better often 1024 X 1024 can be as high as 2048 X 2048 $$$ Display & Display Matrix: Contrast CT #range -1000 to 3000 Monitor can display far fewer gray shades Eye can discern few gray shades Purpose of Window & Leveling display only portion of CT # values Emphasize only those CT #’s display of CT #’s above & below window all black OR all white Pixel Values & Gray Shades # of valid pixel values depends on bit depth 1 bit: 2 values 2 bits: 4 values 3 bits: 8 values 8 bits: 256 values 10 bits: 1024 values n bits: 2n values Pixel Values & Gray Shades CT can discern ~ 4000 gray shades Typical bit depth: 10 bits = 1024 gray shades Single gray shade represents range of pixel values Silly CT # Display Example: 10 Gray Shades >700 651-700 601-650 551-600 501-550 451-500 401-450 351-400 301-350 <301 CT # Level Change Darks lighter lights lighter CT # Level Change >700 >200 651-700 151-200 601-650 101-150 551-600 51-100 501-550 1-50 451-500 (-49)-0 401-450 (-99)-(-50) 351-400 (-149)-(-100) 301-350 (-199)-(-150) <301 <(-199) Window: 400 Level: 500 CT # Level Change 3000 Window: 400 Level: 0 >700 >200 651-700 151-200 601-650 2000 101-150 551-600 51-100 501-550 1-50 1000 451-500 (-49)-0 401-450 (-99)-(-50) 351-400 0 (-149)-(-100) 301-350 (-199)-(-150) <301 <(-199) -1000 CT # Window Change Darks darker, lights lighter CT # Window Change >700 >900 651-700 801-900 601-650 701-800 551-600 601-700 501-550 501-600 451-500 401-500 401-450 301-400 351-400 201-300 301-350 101-200 <301 <101 CT # Window Change Window: 400 Level: 500 3000 Window: 800 Level: 500 >700 >900 651-700 801-900 601-650 2000 701-800 551-600 601-700 501-550 501-600 1000 451-500 401-500 401-450 301-400 351-400 0 201-300 301-350 101-200 <301 <101 -1000 Pixels & Voxels Pixel is 2D component of an image Voxel is 3D cube of anatomy CT reconstruction calculates attenuation coefficients of Voxels CT displays CT numbers of Pixels as gray shades Pixel & Voxel Size Voxel depth same as slice thickness Pixel dimension field of view / matrix size 256 pixels FOV = 12 inches 12 inches Pixel size = -----------256 pixels Pixel size = .047” CT Systems X-Ray Production X-Ray Tube Generator Detectors X-Ray Detection A - D Conversion Reconstruction Display & Format Computer Systems Printing Archiving CT Advantages Excellent low-contrast resolution sensitive detectors small beam size produces little scatter Much better than film CT Advantages Adjustable contrast scale window / level Other digital image manipulations filters bone / soft tissue edge enhancement Region of interest analysis CT Advantages Spiral volume data acquisition in single breath hold no delay between slices improved 3D imaging improved multi-planar image reformatting Special applications bone mineral content radiation treatment planning CT angiography CT Advantages Muti-slice Scans at much greater speed OR Allows scanning of same volume with thin slices Makes possible additional clinical applications CT Disadvantages Poorer spatial resolution than film Higher dose to in-slice tissue Physical set-up can limit to axial / near-axial slices Artifacts at abrupt transitions bone / soft tissue interfaces metallic objects