* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download SHORT TITLE OF THE THESIS CARDIOVASCULAR SYSTEM
Cardiovascular disease wikipedia , lookup
Heart failure wikipedia , lookup
Electrocardiography wikipedia , lookup
Management of acute coronary syndrome wikipedia , lookup
Coronary artery disease wikipedia , lookup
Antihypertensive drug wikipedia , lookup
Cardiac surgery wikipedia , lookup
Jatene procedure wikipedia , lookup
Heart arrhythmia wikipedia , lookup
Dextro-Transposition of the great arteries wikipedia , lookup
SHORT TITLE OF THE THESIS
CARDIOVASCULAR SYSTEM: POWER CONSUMPTION OPTlMIZA TION
©PTlMIZATION IN THE CARDIOVASCULAR SYSTEM: A STUDY OF
POWER ( OXYGEN CONSUMPTION ) AS A PERFORMANCE CRITERION.
ABSTRACT
In this work, a search is conducted to find the relevant
performance criterion in the mammalian cardiovascular system,
It has been assumed that this system actively adjusts its
operating parameters to minimize its power consumption.
part~cular,
In
several combinations of stroke volume and heart rate
may satisfy the system demand for a given cardiac output, while
maintaining a mean arterial pressure set by the baroreceptor
feedback loop.
According to the hypothesis, the optimum com-
bination is the one for which a minimum oxygen (power) consumption
i s obtained.
New experimental data on dog hearts have been
obtained showing that a minimum of this performance criterion
is indeed achieved at rates observable in the resting animaIs.
The results also indicate that an inverse relation exists between
size and optimum frequency of the heart which has been observed
by other researchers in a different context o
ROBERT DEMERS
M.Eng.
Electrical Engineering Department
McGi11 University
OPTIMIZATION IN THE CARDIOVASCULAR SYS'lEM: A STUDY OF
POWER (OXYGEN) CONSUMPTION AS A PERFORMANCE CRI'lERION.
OPTIMIZATION IN THE CARDIOVASCULAR SYSTEM: A STUDY OF POWER
(OXYGEN) CONSUMPTION AS A PERFORMANCE CRlTERION.
by
ROBERT DEMERS
A thesis submitted to the Facu1ty of Graduate Studies and Research
in partial fulfillment of the requirements for the degree of
Master of Engineering
DEPARTMENT OF ELECTRICAL ENGINEERING
McGILL UNIVERSITY
MONTREAL, CANADA
AUGUST, 1968
®
Robert Demers
1969
ACKNOWLEDGEMENTS
l wish to express my appreciation to Drs. J.H. Milsum and
L~D.
MacLean
for encouraging and guiding my efforts in this interdisciplinary endeavour.
Dr. Milsum has directed my theoretical work in the bio-engineering sciences.
Dr. MacLean has given his full support to the realization of,Othis thesis.
l am greatly indebted to Dr. S.
Pitz~le
who is largely responsible for
the successful complet ion of the experimental part of this report.
l wou Id
also like to acknowledge the contribution of the technical personnel of Dr,
Pitz~le's
laboratory.
l must also record my gratitude to aIl of those who have given their
time and advice during the course of this work.
l would like to thank Miss Joan Beckett for typing this thesis at the
expense of her leisure time.
• • • • • • • • • • • • •
Enfin, je me dois de souligner l'étroite collaboration de mon épouse
Colette dans la rédaction de ce rapport et l'important support moral de
Marie-Julie, notre petite fille
~ütousdeux.
Robert Demers
TABLE OF CONTENTS
CHAPTER I
INTRODUCTION
1.1.
1.2.
1.3.
1.4.
1.5.
Subj ect of the the si s
Optimization in biological control systems
The cardiovascular system: an adaptive system
Performance criterion
Outline of the thesis
CHAPTER II
THE CARDIOVASCULAR SYSTEM
2.1
2.2.
2.2.1.
2.2.2.
2.3.
2.4.
2.5.
2.5.1.
2.5.2.
2.5.3.
2.5.4.
2.5.5.
General organization of the circulation
The components: anatomical details
The heart
The vascular beds
Goneral features of the circulation of blood
Dynamic modelling and functional block diagram
Control in the cardiovascular system
General
Control centers
Control parameters
Control structure
Functional block diagram
CHAPTER III
DEFINITION OF THE OPTIMIZATION PROBLEM
General
3.1.
Uncoupling the sub-system
3.2.
Definition of the problem
3.3.
3.3.1. Heart rate - stroke volume optimization
3.3.2. A second optimization problem
Potential solutions
3.4.
3.4.1. General
3.4.2. Data from animaIs
3.4.3. Adaptation mechanisms
Optimizqtion in vivo
3.5.
1
1
1
2
2
4
7
7
8
8
10
10
13
18
18
19
19
21
21
25
25
26
27
27
29
30
30
32
33
35
CHAPTER IV
PERFORMANCE CRITERIA
4.1.
4.2.
4,2.1.
4.. 2.2.
4.3.
4.4.
4.4.1.
4.4.2.
4.4.3.
4.4.5.
Pre1iminary considerations
. Hydraulic power output of the heart
Definitions
The frequency dependence of the hydraulic power
output of the heart
The hydraulic power output of the heart: an
unacceptable performance criterion
A new hypothesis
Review of literature on power consumption in
cardiovascul ar system
Preliminary considerations
Sites of power consumption
Oxygen consumption rate: as a measure of power consumption in the heart
Relation of myocardial oxygen consumption to systemls
variables and parameters
Discussion
CHAPTER V
THE EXPERIMENT
5.1.
5.2.
5.3.
5.4.
5.5.
5.5.1.
5.5.2.
5.5.3.
5.6.
5.6.1 ...
Objective and conditions of the experiment
Historica1 deve10pment
The apparatus
Surgica1 Procedure
Measuring techniques
Instrumentation
Data acqui si tion
B100d gas analysis and détermination of oxygen
consumption rate
Data processing
Digitizing procedure
CHAPTER VI
RESULTS ON THE MEASURED PERFORMANCE CRITERION
6.1.
6 .. 2.
6.2.1.
6.2.2.
6.2.3.
6.2.4.
General
The resu1ts from physiologica1 point of view
Preliminary remark
Mechanical performances
Coronary flows
Relation between 02 consumption ~ate and tensiontime-index
36
36
37
37
39
42
43
44
44
44
45
47
51
55
55
55
57
59
61
61
62
63
66
66
69
69
70
70
70
73
74
CHAPTER VI - cont 1 d
6.3.
6.4 ..
6.4.1.
6.4.2.
6.4.3.
6.4.4.
Constancy of mean arteri al pressure and cardi ac output
The evaluation of the performance criterion from the
experimental data
General
Basal metabolism
Correction for the effect of deviations from the
problem constraints
Polynomial regression and derivation of the optimum
frequency
CHAPTER VII
OPTIMIZATION OF POWER CONSUMPTION IN THE CARDIOVASCULAR SYSTEM: THE
COMPONENTS OF THE OXYGEN CO ST
7.1.
7.2.
7.3.
7.4.
CD
7.4.1.
7.4.2.
7.5.
7.6.
7.6.1.
7.6.2.
7.6.3.
7.6.4.
7.7.
General
Components of the oxygen costs
Mechanical power output: frequency dependence
Developed tensile stress: definition and frequency
dependence
Preliminary remarks
Estimation of the Tensile Stress Index (TSI)
Possible components of oxygen consumption
Estimation of the hydraulic input impedance of the circuit
Concept of hydraulic input impedance
Techniques
Resul ts
Comparison with in vivo impedance
Conclusion
CHAPTER VIII
FUTURE WORK AND CONCLUSIONS
8.1
8.2.
8.3.
8.4.
General
Contributions to the optimization problem
Unsolved problems and limits of the experimental work
Future work
75
76
76
77
78
81
87
87
88
90
92
92
94
98
100
100
101
102
102
103
104
104
104
106
106
APPENDIX I
APPENDIX II
109
REFERENCES
118
112
'"
".
,>.
CHAPTER 1
INTRODUCTION
1.1.
Subject of the thesis
In broad terms, this work is concerned with optimization in the
mammalian cardiovascular system.
In particular it is concerned with the nature of the relevant performance criterion by which' this system selects its operating parameters, in
order to optimize its overall behaviour for the benefit of the whole organisme
1.2.
Optimization in biological control systems
The idea of optimization in biological systems emerges from the
principle of natural selection whereby individuals, species and societies
that can adapt best to the particular conditions in a given environment have
an advantage over the others in terms of their survival.
This concept has
been present in a more or less defined way in the mind of many physiologists,
including cardiovascular researchers (see Taylor, 1964 for example).
From an engineering viewpoint, it is natural to hypothesize that the
adaptation is carried out in terms of the physical laws governing the forces
acting and determines the optimum parameters of the structures, such as their
dimensions and shapes.
This has been stated
Optimal Design (Rashevsky, 1960).
fo~ally
as the Principle of
A further stage of the optimization
process concerns the active pursuit of an optimum state when the system is
in operation.
The problem then arising in the study of the biological
control systems, is analogous to the one the adaptive systems design
engineer is faced with, namely, the determination of the particular control
configuration carrying out the optimizing procedure (p.414, Milsum, 1966a).
2.
The solution is not a simple one since the analyst is usually faced
with a whole hierarchy of interacting control systems existing even within
any one individual o
1.3.
The cardiovascular system: an adaptive system
The mammalian cardiovascular system, along with many others devoted to
the maintenance of the milieu int{rieur, is mainly concerned with the circulation of blood within the body.
In human adults, the blood flow demands may
vary from 4-6 liters per minute at rest ,to 25-30 in heavy exercise.
In order
to produce this, the heart, which·is a pulsatile flow source, delivers from
1 to 10 watts of hydraulic power to the distributing network of vessels, and
the total metabolic energy turnover is in the range: 20-100 watts.
This per-
formance is continuously monitored by active controls, and a great number of
mechanisms is involvedï both, for example, in the fast and precise adjustment
of the blood pressure, and in the slower adaptation that may affect the
structural characteristics themselves, such as the mass and volume of the
heart.
A few of the feedback control loops are known, but the picture con-
cerning the adaptive processes is not clear at aIl (an ignorance applying
equally weIl for Most other body sub-systems).
With this present lack of
full knowledge, an adequate analysis of the active optimization process
remains a long term objective.
1.4.
Performance criterion
In view of our ignorance of the controlling systems engaged in the
:.
a
optimization task, it has been proposed to study the nature of the performance criterion, on the basis of which the course of an activity isdetermined
(Milsum, 1966b).
In essence, the performance criterion represents the total
cost (or profit) imposed on the system by a given situation and usually
3.
consists of a weighted sum of the individual costs associated with different
aspects of the system operation.
In biological systems, the energy required or consumed in performing a
given task often represents a meaningful cost.
These energy costs are
essentially dependent on the system's dynamics, and the se latter are easier
to study from both the experimental and theoretical points of view than the
controlling systems.
Consequently, the search for such performance criteria
is justified as a way of tackling the optimization problem in biological
systems handling relatively large amounts of energy.
This approach has been
successfully applied in two of the body's sub-systems, namely in respiration,
where the frequency of breathing chosen is that for which the work is minimum
for any given ventilation rate (Christie, 1953) and in the walking process
where the step frequency chosen is that associated with a minimum power
consumption for any given velocity (Cotes and Meade, 1960).
The search for an energy related performance criterion is also highly
relevant for the cardiovascular system since significant energy costs are
involved.
However, no formaI evidence has yet been produced that the oper-
ating parameters in this widely investigated system are selected by an
optimizing scheme similar to the others already mentioned.
Therefore the
main objective of the present investigation is to determine the nature of
the relevant performance cri terion in the cardiovascular system.
Although the emphasis is on the energy aspects in this work, it is
understood that for a more complete optimization including such processes
as diffusion of gases (oxygen) from and into the blood, etc., the more appropriate variable may be related to entropy (Wilson, 1964 and 1966j Mi1sum,
1968).
4.
1.5.
Outline of the thesis
The following paragraphs outline the method of analysis adopted.
This
approach is characterized in general by the trial and error method, since an
"a priori" selection of the perfonnance criterion is necessary.
It is first
assumed that the in·:-vivo values of the parameters have been optimized by the
evolutionary processes, and that consequently a suitable performance criterion
must gi ve optimal parameter
values close to those observed.
we have used in succession, the
As "candidates",
hydraulic power output of the heart,
and the metabolic power consumption of the heart since those have been successfully tested in other systems.
In chapter II of this thesis, the anatomical components of the cardiovascular system are briefly described, and the general features of the
circulation of blood in the body depicted.
A simplified "black box" diagran
of the system dynamics is presented to avoid lengthy mathematical considerations,
and the essential control loops at the lower level of the adaptive processes are
introduced.
In chapter III, the problem of optimization in the cardiovascular system
is defined.
A first problem :' deri ved from analogy wi th other systems; i8 the
selection made among the possible combinations of heart rate and stroke volume
to satisfy a given cardiac output.
It is assumed that the pursuit of an optimum
set of these parameters is entirely carried out by the "uncoupled" system.
However, an additional constraint is brought in by the arterial pressure feedback control loop whereby the cardiac output must be delivered at a "set" mean
arterial pressure over the range of parameter variations.
Experimental data
are av ail able to show that these operaLing conditions are still satisfied by
5.
several stroke-volume and heart rate combinations and therefore the
of optimization may be carriedout further.
~al:ysis
It is also remarked that a
second optimization problem consists in finding the optimum among the possible
pressure settings of the arteri al "barostat".
In chapter IV, the analysis of the performance criterion is started.
It emerges that the hydraulic power output of the heart is not an appropriate
measure of the system' s cost in the cardiovascular system.
Instead, the power
(oxygen) consumption per unit cardi ac output is proposed as a performance
criterion.
Data derived from published works on myocardial oxygen consumption
provide encouraging but insufficient information about the hypothesized criterion
Hence, new experimental data are necessary.
In chapter V, an experimental set-up is described in which hearts from
dogs are connect-ad to an artifici al circuit and paced at various "set" frequencie
Details are given of the surgical procedures, the measurement techniques and the
data processing.
In chapter VI, it is shown that the data from these experiments compare
well with other data obtained from normal dogs, and that the constraints of the
optimization problem are reasonably satisfied.
The results on the performance
criterion indicate that a minimum is achieved for one combination of heart rate
and stroke volume in four out of the five cases studied.
Furthermore, our
data show that the optimum frequency is inversely related to the size of the
heart, a fact already observed in··vivo.
Chapter VII is concerned with two aspects of optimization.
First, the
aspect of competition between the components of the total measured cost
is
6.
discussed.
The data indicate that the hydraulic power output decreases
significantly with increasing frequencies while the developed tensile stress
increases.
However, measurements necessary to draw a conclusion on this
aspect cou Id not be obtained with the available instrumentation.
The second aspect is concerned with the differences between hydraulic
input impedance of the circuit connected to the hearts in our experiment and
the "in vivo" impedances.
In chapter VIII, conclusions are drawn and further work is proposed.
7.
CHAPTER II
THE CARDIOVASCULAR SYSTEM
2.1.
General organization of the circulation
The primary task of the cardiovascular system is to circulate blood through
the various parts of the body, so as to produce appropriate exchange both with
the cells of the body and with the environment via the lungs specially.
The
circulation is effected in a closed circuit (fig. 2.1) by a double pump organ,
the heart, connêcted to two networks of vessels; the pulmonary and the systemic
vascular beds.
Venous blood is pumped by the right ventricle into the lungs
where is liberates carbon dioxide and becomes "arterial", i.e. saturated with
oxygene
From the lungs, the blood returns to the left part of the heart to be
pumped by the left ventricle into the body organs.
Within these organs, the
oxygen in the blood diffuses through the walls of the minute capillaries to be
used up by the tissues for their metabolic activities.
This oxygen removal in
the capillaries is accompanied by the absorption by the blood of the carbon
dioxide released by the oxydation processes of the cellular metabolism.
The
deoxygenated or venous blood flows out from these organs and is conveyed
into the systemic veins to the right heart completing the circuit.
The cardiovascular system in addition to this vital "pumping" of oxygen
from the lungs to the cells is also responsible for transporting other materials
(nutrients) and information (hormones).
These numerous tasks are accomplished
efficiently because of the special carrier properties of the blood.
It is
therefore essential to make a distinction between, on the one hand, the mechanical
pumping of the blood, and, on the other hand, the transport of different substances by the circulated blood.
In the latter case, sever al interacting systems
Pu 1monary vascu lar bed
1
1
arterial blood
venous blood
Left atrium
Ri ght ven tri c le
Left ventricle
•
Systemlc
1
vascu lar bed.
Fig. 2.1. The circulation of blood within the body
8.
are involved,
e~g.
the oxygen transport is effected by the chain made up of
the respiratory and the cardiovascular systems terminated by the metabolic
processes.
In the first case, one refers more specifically to the structures
interacting with an hydrodynamic: fluid, and the associated controls.
This
last point of view is the one adopted in the present study and from now on the
cardiovascular system is considered as a pure hydromechanical system.
2.2.
The components: anatomical details
It is now pertine,nt to consider briefly the anatomy of the main compon-
ents of this mechanical system, before discussing how the circulation of blood
is achieved and controlled.
2.2.1.
The heart
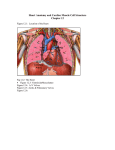
The mammalian heart (see fig. 2.2) is a four chamber organ which constitute:
two separate pumps, each made up of a receiving chamber, the atrium, and a
pumping chamber, the ventricle.
The left ventricle is approximately ellipsoidal
while the right ventricle isformed by a fIat wall extending around one side of
this ellipsoid and is :separated from the left ventricle by the intraventricular
septum.
The thick ventricular walls are consti tuted from an arrangement of muscle
bundles that run circularly and obliquely and are attached to a skeleton of four
fibrous rings.
Each ventricle has an inlet and an outlet orifice guarded by
valves that have their bases on these fibrous rings.
The inlet
atrio~ventricular
valves namely, the left bicuspid and right tricuspid valves al.e respecti vely
composed of two and three leaflets which occlude the orifice by coming together.
These leaflets are attached from inside the ventricles to the papillary muscles l
--
41)
Aorta
CI
Pulmonary veins
P. T.
pulmonary trunk
R.A,L.A right and left atrium
Superior
vena cava
R. V ., l. V
right and left
ventricle
fi brous rings
bicuspid valve
Inferior
vena cava
sa
av
tricuspid valve
papillary muscles
sino atrial node
atri.:wentricular node
Bundle of His and
Purkinge system
Fig. 2.2. The Heart : anatomical details.
9.
fibrous threads (chordae tendinae) to prevent their reversaI during contraction.
The aortic and pulmonary outlet valves are each made up of three semilunar cusps
that are held closed against the backflow in the connected outlet vessels, the
ascending aorta and the pulmonary trunk respecti velYe
The atria are thin walled chambers operatingat low pressures of a few
centimeters of water and they provide useful cross-section matching between the
ventricle and the connected vessels namely, the venae cavae and the pulmonary
veins on the left and right side respectively.
These atria are also isolated
electrically from the ventricle by the fibrous rings.
It is generally agreed
that the atria improve the pumping of the heart by producing late diastolic
distension of the ventricle but this effect is not quantitated yet significantly.
The electrical conduction system of the heart
Within the anatomical limits of the heart, specialized groups of muscle
cells form:
1)
the sinoatrial (SA) node in the wall of the right atrium near the
superior vena cava,
2)
the atrioventricular (AV) node, in the interatrial septum above the
coronary sinus,
3)
the bundle of His and the Purkinje system which has fibers distributed
throughout the ventricular myocardium.
These structures are responsible for
generating the electrical impulse initiating the atrial contraction (SA node)
and for ensuring the transmission of this impulse after sorne delay (AV node) to
the ventricular fi bers via the Bundle of His and the Purkinje system.
10.
2.2.2.
The vascular beds
The blood is pumped by the heart into a very extensive networIc of vessels.
The walls of these blood vessels are composed of four structural componentsi
the rubber-like elastin and the less extensible collagen fibers, the actively
contracting smooth muscles and the endothelial "lining" cells.
In fact, the
blood vessels form a continuous membrane throughout the body and the varying
physical properties along this membrane are due to the varying relative pro-r
portion of these components.
Segments of this membrane with similar properties
are given connnon anatomical nanes.
The two vascular beds, pulmonary and systemic, have a similar geometry.
Each is produced by division from a single vessel, respectively the ascending
aorta and the pulmonary trunk, into major arteries which then subdivide into
branches, terminal branches, arterioles and capillaries.
The latter number
approximately 109 and have a total cross-section of 600 cm 2 in the systemic bed
of a dog.
The blood returns to the other side of the heart through successive
pathways of venules, branches, termdnal veins, large veins, gradually converging
to the main vessels connected to the atria.
Table 2.1 gives sorne details con-
cerning the geometrical dimensions of these various segments, their number, the
resulting total cross sectional area and the flow velocities, for a dog with a
2.4 l/min cardiac output.
2.3.
General features of the circulation of blood
The circulation of blood centrally (near the heart) is characterized by
the high velocity pulsatile nature of the flow as generated by the necessary
phasic mode of operation of the heart.
Peripherally, the blood perfuses the
11.
TABLE 2.1+
APPROXIMATE DIMENSIONS AND BLOOD VELOCITIES IN VARIOUS SEGMENTS OF THE
CARDIOVASCULAR SYSTEM FOR A 13-kg D06, ASSUMED CARDIAC OUTPUT: 2.4 l/MIN.
SEGMENT
Number' Di amete~ , Cro s s 1Length Vo1mm
ume,.
sect~on.
ml
cm .
Left atrium
Left ventricle
Aorta
1
Large arteries
40
Main arteri al branches
600
Terminal arteries
1,800
Arterioles
40 x 106
CapillaI'ies
12 x 108 "
Venu1es
80 x 106
Terminal veins
1.800
Main veins
600
Large veins
40
Venae cavae
1
Right atrium
Right ventric1e
Main pu1monary artery
1
Lobar pu1monary artery branches
9
Smal1er arteries and arterio1es
Pu1monary capillaries
6 x 102
Pu1monary veins
Large pu1monary veins
4
10
0.8
3
3.0
1
5
0.6
7.0
0.02 125
0.008 600
0.03 570
1.5
30
27
2.4
11
6.0
12.5
1.2
12*
4*
1.1
1,19
0.008 300
Blood
ve10city
cm/sec
25
25
40
20
10
1.0
0.2
0.1
0.2
1.0
10
20
40
2.4
17.9
)
)
0.05
)
)
30
60
50
5
25
60
114
30
270
220
50
25
25
24
18
16
52
* Mean of mcüor and minor semiaxes of the e11iptic cross section.
+ Obtained from E.O. Attinger, in Pu1sati1e B100d Flow.
Inc., 1964.
Mc6raw Hill
50
13.4
8
6
0.32
0.07
0.07
1.3
1.48
3.6
33.4
36.4
33.6
0.14
12.
capi11ary bed in non.pulsatile flow at the low velocities necessary for efficient
gas exchanges to take place (see column 6, Table 2.1).
The heart ventricles are filled' passively from the venous side through
the atria during
The atria1 contractions produced by the SA node
diastol~.
'1'
discharge completely the ventricular fillings.
cular contractions (systole).
This 'is followed by the ventri-
First, the tension generated by the activated
ventricular fibers rapidly build's up the contained blood pressure, and when the
pressure gradients are overcome, the outlet valves open and the maj or part of
this blood is ejected into the outlet vessels.
The flow
i~
greatest initially
and then decreases until a backflow of short duration closes the valves.
action produces approximately triangular flow
aorta and the pulmonary trunk.
w~ves
This
in both the root of the
As a result of the rapid succession of these
flow pulses (72/min in man)! a considerable d.c. pressure level (80 mm.Hg
systemici 18 mm.Hg pulmonary) is built up in the arteries, on top of which
pressure waves are superimposed', and transmi tted as pulses as far as the
arterioles.
The flow and pressure become progressively more steady as the
blood advances into the network of arteries.
As the capillaries are approached
the flow is essentiallycontinuous with a d.c. pressure existing.
In passing
through the arterioles and through the capillaries, the blood has to overcome
considerable viscous forces.
In the systemic side for exemple, these forces
cause a pressure drop of more than 40 and 20 mm.Hg respectively across these
segments of the vascular bed.
In 'thi s respect, i t should be noted that the
pressure drop varies as the inverse of the fourth power of the vessel radius
(Poisseuille's law).
Besides this energy dissipation, a transformation of
Jdnetic into potenti al pressure energy also occurs.
Indeed, as the total cross-
sectional areas of the vascular beds increase,. the flow is decelerated.
As
shown in Table 2.1 the high velocities of around 50 cm/sec present in the
arteries reduce to only .07 cm/sec in the capillaries.
From the capillaries, blood returns to the heart via the veins at low
pressures, with flow of increasing velocity as it proceeds toward the atria.
This acceleration is the result of a decrease cross-sectional area and the
corresponding energy transformation is the inverse of the one described above.
(In both cases, these relations are defined by the Bernouilli's law.)
Several peculiarities are present in the venous part of the circulation.
Because the walls of the veins are collapsible, the cross-sectional areas of
these vessels, hence, the flows, are easily modified by external causes such
as the forces of acceleration and deceleration, changes of gravitational potential
energy due to postural and other changes, respiratory movements, etc.
There
are also valves in the veins of the limbs and sorne pumping is actually produced
when the veins are compressed by muscular contraction.
The contribution of
this pumping may be important particularly in exercise but this has not been
studied quantitatively yet in any significant manner.
Finally, in the large
venae cavae and in the pulmonary veins there are waves produced by a mechanical
backward effect of the heart contraction itself.
2.4.
Dynamic modelling and functional block diagram
In the precedent section, the process of the circulation of blood has been
described.
Our purpose now is to derive a general and simple functional
representation of the uncontrolled cardiovascular system dynamics.
The dynamics
of this hydromechanical system depend on the physical properties of the system's
main components, the heart and the vascular network, and on their interaction with
14.
the blood contained within, the blood being a non-newtonian fluid.
In order to avoid, at this present stage, the complexities and the
constraints of the
approximation~
that are inherent in deriving any mathe-
matical model, the "black box" approach has been used to represent the system
without defining rigouroüsly any particular relationship within the various
boxes.
Fig. 2.3 is a blo'ck diagram of the overall system which illustrates in
particular the parallelism between both the pulmonary and the systemic flow
loops.
The general aspects of the dynamics pertinent to each block are now
briefly discussed.
The systemic-cardiac block is shown with two inputs: the pulmonary
venous pressure Ppv and the aortic pressure Pao feedback from the coupling
arterial admittance.
The output is Fao the rate of outflow from the ventricle.
This particular selection of the input-output variables is justified by the fact
that D.A. Robinson (1965) has demonstDated that the heart acts more like a
source of flow than of pressure, because of the high apparent impedance of the
active ventricle.
The dynamic behaviour of the heart is indeed characterized to a great
extent by the nature of its structural component, the myocardial muscle fiber:
1)
The contractile component of the muscle fiber obeys a force-velocity
relation of the form:
( f + a ) v = b ( fo - f )
= force, v = velocity of shortening, fo = maximum isometric
v = 0) a and b are constants.. l ncident ally, equation ( 2- a )
( 2-a )
where f
force
(when
i s in fact
e
e
SA
node
lEFT
HEART
pacemaker
PULMONARY
r
f~
~
~
v
l
muscle
e
(Ô)
'V
shape
l.
~
1
--.J1
/---,l-
-
COUPllNG
arterial
Admittance
_
_
_
_
Fao
Pao
r
--1
.-1
Arterioles
Capillaries
FlLp
Pa
'v
r
Ppv
1
/
SYSTEMIC
X
J
Psv
Venous Admittance.-=:.J
Fig. 2.3. Block diagram of the uncontrolled Cardiovascular System.
1
--1-
l~
-F-
s
Fp
/
1
15.
the Hill's equation derived long ago for skeletal muscle (Hill, 1938) but
with different values for the constants a, b, and fo.
The other properties
mentioned below are also found in the skeletal muscle.
2)
The force actively developed fo is also a function of the length L
of the contractile component:
fo = fo ( L )
3)
( 2-b )
A passive elastic component exists in series with the active con-
tractile component, in which the tension is exponentially related to the elongation.
,
4)
component
Another passive elastic/is present that causes a tension rise when
the non-activated fi bers are stretched.
These properties were verified initially by Sonnenblick (1962, 1964 and
1966) in isolated strips of papillary muscles but are n(JN. currently studied in
the whole heart (Fry et al, 1964; Levine et al, 1966; Covell et al, 1966;
Forwand et al, 1966).
A special situation is created by the fact that the muscular walls of the
heart chambers contract on a closed space filled with blood.
The pressure in
this fluid is thus a function of the tension in the walls and of the radii of
curvature.
If we consider the simplest geometry of a thin-walled spherical left
ventricle, the relation is:
T
where T
= tension,
r
~
= P2r
ventricular radius and P
( 2-c )
= pressure.
Because of this
physical law, a close dependence exists between, on the one hand, tension and
length changes in the muscle fiber, and on the other hand, pressure and volume
changes in the ventricle.
In our black .. box representation of the cardiac
dynamics, the input venous pressure determines the rate of .filling of the
ventricles during the passive phase of the heart cycle and the resistance to
16.
filling progressively increases with the stretching of the walls.
The resulting
volume at the onset of the active state specifies the initial fiber length.
and consequently also the maximum possible force of contraction fo ( L ).
(Starling's law).
As a result of the above force-velocity relationship, the
ventricular outflow rate Fao depends on the initial (as weIl as the subsequent)
fb and also on the pressure load Pao which is thus fed back to the heart while
being modified by the outflow pulse itself.
This explains the high apparent
internal impedance of the heart as a flow source (150 mm.Hg pressure drop: value
quoted by Robinson (1965),
No attempt has been made here to represent separately the atrium and the
ventricle.
It should be understood however that the atrium plays a secondary
role and is usually ignored in simple analog models.
The pressure wave Pao at the beginning of the arterial system is modified
aU along i t s travel in the arteri al bed unti 1 i t reaches the "end" of the li ne
as Pa
The coupling arterial admittance associated with the long elastic
tapered arterial vessels is in fact a distributed system which has been studied
appropriately and fruitfully in terms of a transmission line (Attinger, 1964).
/
Of sorne interest in a later portion of this work is the particular pressure
-flow relationship at the inlet of the arterial bed which is termed the hydraulic
input impedance and as such is a complex and frequency dependent quantity.
Typically in dogs, (fig. 2.4) the amplitude attenuates from 7 - 9 x 10 3 dyne
- sec cm-5 at zero frequency down to about 0.2 - 0.4 in the 2-10 cps range.
The phase gradually increases from minus 50 degrees around reps to zero at
6-8 cps, '.The tennination of the arteri al coupling line consists of the
arteriole-capillary beds e
These latter are considered to have only linear
8.st
-
HYDRAULIC
INPUT
IMPEDANCE
C")
o
Il")
Aorta -
1.0
1
E
u
u
Q)
411
1
Q)
.8
C
>-
Pulmonary artery - - -
"
.6
\
/-_.
\
\
w
U
\
Z
\
~
w
., ,
c..
~
.
, .-- -- ."'"
.~,
,.
...
/
~
.""".,...-
.
./'
Harmonie no.
4
2
6
8
10
O~--~--+---~--~~~~--~---+---L--~-------------
6.4
+60
0)
Q)
,,
"w
•
V" "
V')
<01(
J:
-60
e
cps
FREQUENCY
0
c..
12.8
J
j"'-'
\//.
Fig. 2.4. Input impedanees of the pulmonary and systemie
vaseular beds in the dog. Data from Q'Rourke:
Cire. Res. 20... 365, 1967 ,and from Mi Inor:C ire. Res.
19; 467, 1966.
D
17.
resistive properties, i.e. a linear relationship exists between the pressure
input Par and the systemic flow output Fs (see fig. 2.3).
The next block is the venous admittance which collects the capillary
flow.
It is characterized by a large value of the compliance (ratio of volume;
and pressure changes), because veins can accommodate large volumes of blood
without correspondingly large pressure increases.
Provisions must be made in
the der.ivation of an appropriate transfer function for this venous block to
incorporate several non-linear effects such as the venous "pumping" and the
various disturbances "inputs" acting on the collapsible walls of the veins, as
discussed previouslYe
The pressure output Psv of the systemic venous block is fed into the
right heart entering the pulmonary flow loop,
The basic structural components,
muscle and vascular tissues, in this loop, are essentially identical to the one
in the systemic side.
Consequently, the relevant dynamics are very similar to
those just described and differ only by the magni tude of the physical parameters.
They are not discussed any further here.
The pulmonary venous pressure, at the end of the pulmonary flow loop, Ppv
is applied to the systemic heart, closing the circuit and thus creating a
mechanical feedback loop to the systemic circulation.
One must realize that
with such a double-pump fluid circuit, one side could be emptied into the other
if one pump were producing more average flow than the other.
This disastrous
situation is prevented by a self-regulating mechanism present in the heart
whereby the ventricle empties approximately in proportion to its content
(since fo
= foC
L ), and thus eliminates on a beat-by-beat basis anyexcess
volume pushed into either ventricle by the larger pressures created in the
18.
vessels on the corresponding other side.
Other advantageous stabilizing effects which result from the dyn(lIlic
properties of the heart will be pointed out later.
The corresponding mathematical description of the mechanical system of
fig. 2.3 is usually made by representing the vascular network as a series of
lumped passive segments with parameter values depending on the particular
region of the vascu1ar bed.
The heart is either introduced as a forcing
function (de Pater, 1964)Qr its behaviour is approximated by equations derived
from experimental data (Robinson, D.A., 1965).
A major contribution in
model1ing has been made by Beneken (1965), in particu1ar who has deve10ped and
programmed an ana10g model in which 15 simu1taneous equations are sOlved,
inc1uding a non-1inear physical description of the heart.
Mode11ing techniques are usefu1 in providing a workab1e representation
of the system and will be revea1ed as indispensable in this investigation.
However, our effort in this ear1y stage has rather been concentrated on the
obtaining of proper experimenta1 data.
2.5.
2.5.1.
Control in the cardiovascular system
General
Having defined in the b10ck diagram of fig. 2.3, the process responsib1e
for the circulation of b100d in the body, we can now turn to its control aspects.
As a preliminary to such discussion, we consider the relevant nervous centers
and efferent pathways (towards the effectors), and define the relevant control
parameters in the mechanica1 system.
19.
2.5.4 Control èenters
Two centers are 10cated in the medulla oblongatai
1)
The dorsal motor nucleus of the vagus nerve from which impulses
are carried via the vagal trunk to postganglionic neurons present mainly in
- the atri al walls.
2)
The vasomotor center with pressor and depressor areas from which
excitatory and inhibitory fibers descend in the spinal cord and converge on
preganglionic neurons in the sympathetic chain.
the latter neurons are relayed to
The integrated signaIs from
postganglionic neurons which carry their
sympathetic endings to both atria and ventricles of the heart and also to the
smooth musculature of blood vessels, mainly to the arterioles and to the veins.
An additional center exists in the cerebral cortex, designated as the
sympathetic vasodilator system.
The corresponding efferent nerves have
cholinergic endings directed mainly on the muscle blood vessels.
This center
is presumably responsible for the adaptive changes occurring in exercise
specia1ly.
There is in addition to the above channels, a mixed pathway by which
the sympathetic nerve stimulates the adrenal medulla which in turn releases
adrenaline in the blood stream.
2.5.3.
Control parameters
The fiber endings of these efferent nerves release into the surrounding
tissues"either norepinephrine or acetylcholine in amounts depending on the
modulating pulse frequencies.
These chemical transmitters, and sorne other
substances when information transmission is made otherwise than by the nervous
channels, are responsible for actually changing the physical parameters of the
20.
mechanica1 system.
It is thus relevant to discover what these parameters are
and to indicate the mechanisms whereby the parameter changes are effected.
The cardiac nervous inputs modify two parameters, namely the heart
frequency and the muscle contractility.
In particular, the SA node rhythm is
modu1ated by the input frequencies of the vagus and sympathetic nerves that
compete respectively for heart rate slowing or acceleration by modifying the
rate of the membrane potential discharge of the pacemaker cells.
Cox, 1962; Robinson, B.F. et al, 1966).
(Warner, and
The alterations in contractility are
the resu1t of an intrinsic effect of the transmitters on the muscle fibers
themselves accompanied mechanicallyby a variation in the parameters of Hill's
equation, namely, variations in Vmax , derived from 2-a as:
./
Vmax
= V for f = 0
( 2-d )
• •
At any given length of the
~uscle,
a set of force-velocity curves exist that
correspond to the possible values of the contracility parameter Vmax •
(Sonnenb1ick, 1962).
These contractility changes may also be observed from the increased
pressure derivative and rate of ejection at the heart outlets.
Noble et al
(966) have shown for example that the maximum acceleration of flow
in;g!;s..;~.;
increases from control values around 8.6 up to 12.5 cm/sec 2 following injection of a drug acting on the contractile parameters.
_ 1 d Fao
9 - - -A dt
where A
= aortic
in cm/sec 2
root cross-sectional area.
'g' is defined by -
( 2-e )
Simultaneously, the maximum
pressure derivative also increases by about 30 to 50 per cent from say
3000 to 4400 mmHg/sec.
21.
There.are ·also two control parameters acting in the blood vessels,
namely the arteriolar resistance and the venous compliance.
The alteration
of these two parameters are consequent upon variations in the diameter and
ela~ticity:of
the walls effected by the contracting smooth muscle fibers
present in the arterïoles and in the veins.
These fibers are directly
stimulated by norepinephrine. epinephrine and acetylcholine, the latter
substance producing a vasodilating effect.
2.5.4.
Control structure
The al teration of these various parameters based upon the particular
mechanisms mentioned above involve dynamic processes in which interactions
with the system variables (flow and pressure) are also present.
The resul-
tant overall systemdynamics are çonsequently highly non linear.
The functional control: structure relevant in the· cardiovascular system
can be represented in a very general form as in fig 2.5.
One particular
feature of this structure is that the feedback action is achieved through
parameter adjustment, that is, the desired response is: not brought about by
modifying an input but by operating on the controlled system itself o
This
diagrélll illustrates also the two types of feedback loops controlling the
parameters, namely, the organ blood flow loops (local control) and the
arterial pressure feedback loop, shown as an example of central control
loop.
2.5.5.
These will be discussed more specifically in the following chapters.
Functional block diagram
It is possible to integrate in a more detailed diagram, the various
o
•
"
Higher
Centers
CONTROL
SYSTEM
PARAMETERS
VARIABLES
--
Vmax
Centra 1
--
C.V.
Controllers
-
-- CIRCULATION
H.R.
PROCESS
R's
-I...----- T
- ...
1
1
1
f------1
1
1
1
1
Local
1
Flow Loops
1
1- - - - - - - - , 1-
Metabolic
Process
PressoReceptors
-
Organ(s)
______
1
_J
1
_J
Arterial
Blood Flow
Pressure
Fig. 2.5. Block diagram of the controlled cardiovascular system i lIustrating the feedback
through the system earameters. H. R.: heart rate 1 Vmax :maximum shortening
velocity of the cardiac muscle fiber 1 V.C. : compliance of the veins 1 Ris: resistance
of the arterio le-capi lIary beds.
22.
dynamics and the interconnecting information pathways and controllers.
Fig.
2.6 is a tentative block diagram to depict part only of the particular control
scheme adopted by the C.V.S.* The dynamic blocks of the process shown in fig.
2.3 have' been modified in the following way:
1) the pulmonary loop is lumped into a single dynamic component
2) the peripheral resistive bed has been divided into several resistances associated with the various organs with the same pressure input Par but
~th
flow outputs FI, Fi ••• Fn corresponding to the resistances RI, Ri •• ~ Rn.
Columns 3 and 4 of Table 2.2 gives the values of resistance conventionally
quoted, which are associated with functionally different capillary beds.
Of
course, this table could be further broken down, in particular for skeletal
muscle which is distributed in various proportions throughout the body.
3) these "boxes" represent the combined dynamics associated with both
the parameter changes and the pressure flow relationship.
Control inputs come from the central controllers via the nervous pathways and also in the case of the resistive beds from the surrounding tissues
through chemicals carrying a dilating (or constricting?) signal ..,
Control Loops
Two types of control loops are present in the block diagram of fig. 2.6;
the first is involved in a local auto regulation of the organ blood flows,
the second is regulating sorne "central" variables measured by appropriate
receptors that feedback to the nervous controllers.
Locally, the various organs, can alter the resistance of their arteriolecapillary beds, presumably by the action of the metabolites released by their
activity.
I!C
C. V.S.:
The controlled variables in these loops are more properly the
cardiovascular system.
g
•
"
Baroreçeptors
-
Arterial pressure P
a
ORGAN
VASO
MOtOR
,
..... ~
-- -'
Fao
LEFT
HEART
a
,
VAGUS
BEDS
Cardiac
1
sympathetic Vmaxl
CENTER
Dorsal
motor
nucleus
RESISTIVE
sa ~
node
HR
Il
r-------
-- ' - - - - - - - COUPLING
ADMITTANCE
Pa
.....
~
Vagal
tone
I-
""""
r-
Ppv
1
1
r----
,
Pù1monary lo(',p
Dynamics
Psv
---
From Cortex
VENOUS
ADMITTANCE
L-.
L..""i
L-.
f
tone
Vasomotor tone
('
P~Ri
~f
-
vasodilator
Fig. 2.6. Block diagram of the cardiovascu lar system.
F·1 1
1-
I
1
I
L-
•
Venimotor
-
r--
Pao
Metabolic proces!
Fl
U'
Fni 1
11
'Ir
1
22-a
TABLE 2,2
REGION
BLOOD FLŒJ
(ml/min)
RESISTANCE
(rnmHg/ml/sec)
OXYGEN CONSUMPTION
Total
Per 100 gm wt
Total
Per 100 gm wt
Total
Liver
1500
57,7
3.6
9.4
'51
2,0
Kidney
1260
42,0
4,3
1.3
18
6.0
Brain
750
54.0
7,2
10.1
46
3.3
Skin
462
12,8
11.7
42.1
12
0,3
Skeletal
muscle
840
2.7
6,4
198.4
50
0.2
Heart
muscle
250
84,0
21 .. 4
6.4
29
9.7
Others
336
1,4
16,1
383,2
'44
Op2
5400
8,6
1.0
63
250
0,4
Whole Body
Data from Ganong W.F.
Review of Medical Physiology,
Publication, Los Alfos, 1963,
Per 100 gm wt
Lange Medical
D
oxygen requirements of the tissues that impose flow demands in relation to
the oxygen tension or content in the blood (see columns 5 and 6, Table 2.2).
Blood pressure control
Quoting here from Bayliss, "rather li ttle i s known about the way in
which these (the local regulators) control systems operate.
They could not
be effective however unless there were arrangements by which the pressure of
the blood in the main supply trunks (the large arteries) was kept more or
less constant".
(Bayliss, 1966).
A "pressostat" mechanism has therefore
been implemented by nature which also serves as a protection for those organs
essential to the whole individual's survival, that is for those organs which
cannot be deprived of
~n
oxygenated blood flow suppl Y for more than critical
short periods of time (about three minutes for the brain).
This compensating
and protective "role has been recognized by most physiologists (see chapter l,
Burton, 1965).
Physically, the arterial pressure is sensed by stretch receptors in
both the aortic arch and in the carotid-artery sinuses, with their afferent
fibers converging on the depressor area of the vasomotor center.
The feed-
back is negative, i.e. in response to the increase in the rate of firing of
the receptors produced by higher pressures, a vasodilation of the blood vessels
occurs as weIl as an increase in the storage of blood in the venous capaci tance
vessels.
There is usually a concomitant decrease in heart rate by separate
stimulation of the cardio-inhibitory center (Ganong, 1963).
Functionally, this mechanism behaves like a servo-regulator and its
frequency characteristics have been studied with the techniques of linear
control theory (Warner, 1958j Scher and Young, 1963).
More recently, the
24.
non-linear aspects have been treated using describing function methods
(Levi son et al, 1966).
However, the important question of how the "set"
pressure is determined is yet unanswered (Rushmer, 1960).
It can possibly
be tackled as an optimization problem, a problem which we discuss later.
Other receptors have been shown to exist in the atrial and the ventricular
walls of the heart, but they have not been included in the diagram since
their roles have not yet been clearly established.
Higher controls
The central blood pressure and the local flow loops are themselves
subordinated to higher level controls"
During exercise for exanple the blood
pressure setting i5 èither overridden or reset and is no longer maintained
at the normal resting level.
The pattern of local flow to the organs is
changed to maximize the flow towards the muscles' blood vessels, while nevertheless sustaining brain and heart requirements (Chapman and Mitchell, .1965).
The control strategy is then becomi.ng extremely complex at this level, since
furthermore other controlling systems, e. g., blood volume control, are coming
into play with additional variable parameters.
Therefore, while the block diagram of fig. 2.6 is a limited and incompIete description of the cardiovascular system, it is nevertheless useful as
a "black box" model on the basis of which the optimization at the intermediate
"central" control level can now be discussed.
25.
CHAPTER III
DEFINITION OF THE OPTIMIZATION PROBLEM
3.1.
General
The purpose of this chapter is to establish that one cao consider as a
sub-optimization problem, that of selecting a given combination of heart rate
and stroke volume in order to achieve the total flow demand in the cardiovascular system.
This sub-optimization problem seems in fact analogous with
that in other systems in which the demaod is satisfied by a rhythmic succession of movements, for example, in walking, where the velocity equals step
length multiplied by step frequency; similarly in respiration, where the
ventilation rate equals tidal volume multiplied by breathing frequency.
Noting then the similarity in the circulatory process, the blood flow rate
equals stroke volume multiplied by heart frequency.
It is easily verified by personal individual experience that there
exi st several possible choices of frequencies at which one can vOluntarily
either breathe or walk at specified rates.
However, the situation is quite
different when we try to verify also the analogous problem in the case of the
heart, since we do not have any direct control of our own heart rate.
One
may suggest at this point that yogis are capable of sorne voluntary control
when they slow down their heart rate in practising their discipline.
It is
however not clear whether the yogis are then still maintaining the normal
resting cardiac output or whether their heart rate slowing is consequent
upon a decrease blood flow demande
At any rate, it seems extremely difficult,
if not impossible, to ascertain directly that the cardiovascular autonomous
controllers are in fact selecting among a set of possible heart rate -
26.
stroke volume combinations and this matter needs to be examined with
sui table experimental data on animaIs.
Furthermore, a more careful defi-
nition of the problem is indicated, on the one hand because of the
intercoupling problem common to aIl sub-systems and, on the other hand
because of the mixed type of local and central controls, a characteristic
of the cardiovascular system, itself.
In the following paragraphs, the assumption on uncoupling the subsystem for optimization is discussed first.
Secondly, the problem proposed
in the above preliminary remarks is defined more specifically taking into
account the control structure prevailing in the cardiovascular system.
Thirdly, the fact that there does exist a set of potential solutions in the
physiological range, is demonstrated from experimental data only.
The con-
cluding remarks concern the "in vivo" optimi zation.
3.2.
Uncoupling the sub-system
In discussing the optimization of a s1,l-b-system, it is assumed that
there are noconstraints or demands from other "coupled" systems which may
necessitate deviation from the sub-system's optimum operating point.
In our
case, an example of undesired coupling would be the hypertension produced
by anoxiai a vasoconstricting signal is th en carried from the chemoreceptors
to the vasomotor pressor area, whereas normally those receptors transmit
their information only to the respiratory system which regulates the gas
content state of the blood, i.e. the p02 and the pC02.
(p.443, Gagnong,
1963). For similar reasons, the adaptation to heavy exercise load is excluded from these considerations.
Indeed, in this last situation, the
overall strategy is presumably determined by higher controls.
D
27.
The "uncoupling" hypothesi s means that the system i s relati vely free
from such overriding commands and thatthe usual inputs to the local and
central flow and presure regulators are sufficient at rest or in moderate
activity.
Of course, only a limited number of these inputs have been shown
in the block di agram of fig. 2 6.
0
In view of the many reflexes that. are
elicited by various stretch receptors in the heart and in the vessels
(Aviado, 1955), it is understood that the corresponding control loops are
part of the uncoupled system and possibly participate in the present optimization scheme.
3.3.
3.3.1.
Definition of the problem
Heart rate - stroke volume optimization
The first optimization problem relevant in the "uncoupled system"
concerns the selection of a best combination of heart rate and stroke volume
from among those possible ones for which a given cardiac output is achieved.
These parameters are mathematically defined by considering the regular
sequence of approximately identical, flow pulses delivered by the heart into
the arteries.
The amount of flow delivered per cycle is called the stroke volume SV
and is defined as:
Sv
=
t
)
dt
( : 3-a )
o
where Fao is the aortic flow rate and T is the duration of the cycle.
mean cardiac outflow rate or cardiac output CO is the amount of flow
delivered per unit time into the aorta and is given by:
The
~.
œ=~
(3-b )
T
Since
( 3-c )
where BR is the heart frequency, then from 3-b
co = BR.SV
(
The cardiac output is considered here as the system's demande
3-d~)
As shown
in the block diagram of fig. 2.6, the total flow demand is actually set
peripherally.
In fact, it is the sum of the flows required separately by
the various organs for their respective metabolism.
Of course, there exist
an infinite number of possible patterns of flow distribution among these body
organs that correspond to a given total flow demande
Obviously, only a
smaller finite number of these patterns are physiologically acceptable and
it is understood that the cardiac output defined as the system's demand is
associated with one or more of the latter.
Finally, it is clear from equation
3-0 that the optimizatlon problem defined here is concerned with the operating
parameters selected by the heart in delivering its cardiac output.
It also appears from the block diagram that the flow demand itself is
constrained by the blood pressure control.
Indeed, at the outlet of the heart v
the flow pulse is transformed into pressure by the coupling arterial admittance
and the resulting average pressure output Poc is regulated by the pressoreceptor feedback.
Inasmuch as there is somewhere in the control loop a set
pressure, the flow demand is only partly controlled by the local loops and
the distribution of flow to the various beds is presumably determined centrally in such a way that this pressure constraint is satisfied by an
appropriate vasomotor tone.
29.
Accordingly the problem has to be redefined and we will now assume that
the constraints are to keep both the cardiac output CO and the mean arterial
blood pressure MBP constant.
The different heart rate stroke volume combinations must then be optimized under these constraints.
This in turn implies that both the d.c.
impedance ( MBP/CO ) and the d.c. mechanical power ( MBP x CO ) in the
arterial system are held constant.
It does not however constrain the parti-
cular time course of the flow and pressure pulses at the"heart outlet and
these are adjusted to satisfy the conditions of the problem over the permissible range of parameter values.
3.3.2.
A second optimization problem
Froin "anoptimization point of view, the set pressure is a constraint
which protects the essential organs of the body.
Therefore above the critical
minimum pressure for which this condition is satisfied, there exists a range
of possible barostat settings.
Thus a second optimization problem consists now in finding what is the
optimum pressure in the cardiovascular system, presumably on the basis of
sorne energy criterion.
The system's demand in this case is still the amount of blood flow
circulated per unit time, but one considers now the various combinations of
arterial pressure and total resistance R of the systemic vascular bed for
which a given blood flow rate is satisfied.
Pa:
CO =T
This is defined by:
30.
It is not evident however whether such a problem is relevant in the
uncoupled system.
On the one hand it seems that a good strategy, in a case
where a critical pressure threshold exists, is to operate somewhat above this
threshold to avoid sounding the alarm too often thus minimizing the number
of emergency calls.
From this consideration alone, one should raise the
operating pressure level above the critical level without necessarily minimizing any energy criterion.
On the other hand, this setting has implications
for the economy of energy in the system, since the arterial pressure level
constitutes a gradient of potential energy against which the heart is working
continuously.
Obviously, a separate and more extended analysis is necessary
to establish how this second optimization problem is resolved.
The dynamics involved are the sane in both problems and eventually the
second optimization aspect will be combined with the first problem into a
more general problem.
However from the present practica1 point of view, it
is preferable to study these questions separately and the present thesis is
concerned only with the optimization of heart rate and stroke volume.
3.4.
Potential solutions
3.4.1.
General
Any optimization problem must be treated according to the three
fOllowing steps:
1)
one considers the set of possible states of the system that satisfy
the specified conditions or constraints.
Each of those suitable states, or
potentia1 solution designates a set of variable and parameter values of the
operating system.
2)
the costs associated with these solutions are determined, according
to the selected performance criterion.
31.
3)
a search is then done to find the minimum among those costs and
the corresponding optimum state.
Ideally, these three steps are carried out with appropriate mathematical
techniques.
However, there is no mathematical description of the circulation
process suitable for a theoretical treatment of the problem.
Furthermore,
it has been realized in the course of this investigation that the use of a
computer model of the cardiovascular system to carry on the optimization procedure with a suitable searching algorithm is not satisfactory in the present
context, although such techniques have often been used for other complex
systems.
The difficulty here lies in the fact that the costs, such as power
consumption cannot be computed with reasonable confidence from the variables
of the system's model as required in using this method.
In principle, step l
could have been carried out with a computer model of the cardiovascular
system obtained from the l i terature, but in view of the assumptions that are
then made, additional search is required to verify conclusions obtained from
such models with appropriate experimental data.
It has in fact been found
that a computer model was not necessary in the preliminary phase of this study.
It is nevertheless essential that aIl of the above steps be carried out
and in the next paragraphs the discussion is concerned with showing the existence
of a set or potential solutions.
First, experimental data is presented
to show that a given cardiac output demand at constant mean arterial pressure
is satisfied by several heart rate stroke volume combinations.
Secondly, the
roles of the system's control parameters and of the heart dynamics in the
relevant adaptation are examined briefly.
32.
3.4.2.
Data from animaIs
Fig. 3.2 obtained from BrUtsaert (1965) illustrates that both cardiac
output and mean arterial pressure are maintained constant over a good portion
of the frequency range.
In particular. normal cardiac outputs around 2.7
liters per minute can be delivered at 125-135 mm.Hg pressures over a range
of frequencies from 60 up to 180 beats per minute.
The stroke volumes then
drop from about 45 down to 15 ml as frequency increases.
were obtained from a group of four anesthetized dogs.
These measurements
Similar data. reported
by the same author, were obtained from unanesthetized animals both at rest
and in exercise.
ln both these conditions, cardiac output levels of about 3
and 4 liters per minute respectively were maintained at heart rates of 55-59,
120 ànd 180 beats per minute, while the pressures were constant around 135
mm.Hg.
It should be noted that in the above experimental cases. the frequency
was under control of an adjustable electrical pacemaker after a conduction
block had been produced by destroying the A-V node.
Brutsaert has indicated
the necessity in this kind of experiment of preserving the heart capacity by
pacing at normal rates in the recovery periode
Otherwise the heart submitted
to the stresses of the surgical procedures may deteriorate or hypertrophy
(Brockman, 1965).
Additional evidence is obtained from the data of Donald and Shepherd
(1964) who compared the responses to exercise both of cardiac denervated
and normal dogs.
In a typical case presented by these authors in their
fig. l, the hearts in two dogs of about the same weight produced a cardiac
output of around 2.0 liters, with the denervated and the normal heart
respectively, beating at 120 and 97 beats per minute.
During exercise
1
1
,
60
90
120
HEART
Fig. 3.2.
1
1
i
150
180
210
RATE
beat/min
Constant cardiac output and mean arterial pressure at different
frequencies of dog hearts under pacemaker control.
33.
the cardiac output in both dogs rises to 6 liters per minute; in the normal
heart, the stroke volume stays relatively constant around 22 ml but the heart
frequency increases to 240; in contrast, the stroke volume of the denervated
heart increases from 16 to 32 and the rate varies somewhat but does not
exceed 180 beats per minute.
3.4.3.
Adaptation mechanisms
The above data confirms the existence of a set of potential solutions,
that is, the poss1bility exists for the cardiovascular system to operate within a reasonable wide range of independently adjustable heart rates and stroke
volumes.
From our point of view, it would then be useful to discover the
particular control strategy adopted in those animaIs which maintained their
cardiac output at various frequencies.
In the absence of any data, the
following remarks based upon others' results from computer models, may be
made concerning the control parameters:
1)
individual large parameter variations do not in themselves produce
correspondingly large flow variation
2)
combined small variations of many parameters may produce wide flow
changes.
For example, a 2 5 fold increase in heart frequency only causes a 35
8
per cent increase in both aortic flow and pressure (see fig. 3.30, p. 145,
Beneken, 1965).
On the other hand, a group strategy has been shown (Table
3.4, p. 160, Beneken, 1965) in which no one parameter is varied by more
than 20per cent; yet a 140 per cent rate of flow increase together with a
20 per cent pressure increase is produced.
Data of the left ventricle
model of D.A. Robinson (1965) are in agreement with this behaviour.
34.
Consequently. the adaptation mechanism, if done by active control, is
calling only for relatively small trimming action in
conditions.
specified
satisfying~the
It is however quite probable that the system's own dynamics
are responsible for its insensitivity to individual parameter variation.
For example, fig. 3.3 from Berglund (1958) shows the relationship between
the stroke work and left atri al pressure obtained from dogs wi th an atrioventricular block (note that left atrial pressure varies somewhat in proportion with the venous pressure Ppv ' the input to the cardiac systemic block
in fig. 2.6).
Up to 50 gram-meters could be delivered in a single stroke by
this 17 kilogram dog at 43 beats per minute.
A decrease in the stroke work
occurs with increasing frequencies which is consequent upon an increase in
the filling impedance of the left ventricle at higher frequencies.
This
dynamic effect is apparently a stabilizing mechanism preventing wide
variations in the total flow rate in the closed cardiovascular circuit, while
such variations could be produced for example by fluctuations in the frequency
of a constant stroke pump.
These data also show the rather large working capacity of the heart
that is not normally used at high
frequencies~
Essentially, the adjustment
of heart rate and stroke volume i s based, from the heart dynamics point of
view, on the length-tension relationship (equation (2-b»
muscle fiber.
of the cardiac
As frequency decreases, more time is available for filling
and the end-diastolic ventricular volume becomes larger with a corresponding
increased initial fiber length.
The contraction itself lasts longer, allow-
ing a larger stroke volume ejection.
It seems also improbable that the
cardiac contractility parameters would be called for in this situation since
the duration of the active state is then shortened (Sonnenblick, 1965) and
consequently, despite the increase rate of ejection, the total stroke
Oog
17 kg.
60
43 b/min
E
.
E
40
Cl
~
Q::
0
~
w
~
0Q::
20
240
lV)
>
-1
O~----'------r-----r-----'_
o
20
LEFT ATRIAl MEAN
40
PRESSURE cmH 2 0
Fig. 3.3. The working capacity of a blocked heart at different
frequencies of stimulation. Redrawn From Berglund.
(Acta Phydol. Scand 42,185,1958)
35.
volume does not necessarily increase.
In this respect, in the paper of
Noble et al, (1965) quoted in the last chapter, the cardiac output was not
affected by the contractility changes brought in when the frequency was kept
constant.
Concluding remarks:
3.5.
Optimization in vivo
Because of the existence of a group of possible solutions, the control-
ling system is faced with the problem of selecting the best one.
A basic
assumption is made throughout this study, that the in vivo normal values of
the parametersare the optimum ones.
As a rule, low rates are usually present
at rest, but individual differences are such that a wide range is considered
as normal.
72 beats per minute is typical in man, and dogs in a semi-resting
state have been reported (Gregg et al, 1965) to beat from 81 up to 122 beats
per minute.
The presence of a continuous predominant vagal tone that slows
the heart, as weIl as the vasomotor tone maintaining the "set" arterial
blood pressure, indicate that an active selection of rate and resistance is
continuously made by the central controllers.
Whether or not, this nervous activity is in fact an active pursuit of
an optimum state cannot be answered before the nature of the relevant performance criterion is established.
As mentioned previously in the introduction,
a trial and error procedure is necessary in this search in which steps 2 and
3 of the optimization problem. (P. 30-31) are in fact carried out.
In par-
ticular, a cost function is assumed and computed (or measured) for the
suitable combinations of heart rate and stroke volume, and the minimum cost
may correspond to an optimum state if the parameter values match
those observed in vivo.
To this latter task we now turne
with
36.
CHAPTER IV
PERFORMANCE CRITERIA
4.1.
Pre1iminary considerations
A critica1 step in the optimization study of bi010gica1 systems is to
infer what performance criterion is being optimized.
It has been mentioned
in the introductory chapter, that energy related functions seem to have been
rather general1y adopted in biological systems.
This trend offers a starting
point in considering the cardiovascu1ar system.
In this respect, it is a1so very encouraging that the design of structures in the vascu1ar bed has apparently been optimized on the basis of an
energy criterion.
In particular, such parameters as the radii of branches and
the angles of bifurcations in the intricate network of vessels can be derived
by minimizing a cost made up of both the metabolic energy necessary for the
maintenance of these structures and the energy losses encountered in overcoming
the associated viscous resistance to blood f10w.
very good confirmation from relevant
geomet~ical
This hypothesis has received
measurements in dogs
(Rosen,
It should not be surprising therefore that the system optimizes its
1967).
operating state on the basis of a criterion somewhat related to the one used
in determining the optimum geometry of its vascular bed.
Suitable performance
criterion candidates appear to be the input and the output powers of the heart
and it is therefore intended in this chapter to investigate on the basis of
experimental data whether these functions are involved in the selection of
the heart frequency at constant cardi ac output and pressure levels.
The following points are treated:
a)
The work output of the heart is estimated in a typical dog and is
37.
shown to be unacceptable as a performance criterion.
b)
A new hypothesis is made that power consumption per unit flow is
minimized.
c)
The literature on the power consumption in the cardiovascular
system is reviewed.
d)
An encouraging conclusion can be reached from the data obtained in
the literature but the critical measurements necessary to demonstrate the
existence, or otherwise of an optimum frequency, are not available.
An experi-
mental program is consequently necessary to realize this study's objectives.
4.2.
4.2,1_
Hydraulic power output of the heart
Definitions
The following considerations on the hydraulic power output of the heart
involve several energy and power terms that need to be defined appropriately.
Per cycle, the work WO done on the fluid by the heart is made up of the
pressure-volume work W and the kinetic energy outflow K (we ignore here the
gravitational potential energy).
WO = W + K
( 4-a )
In turn, these two terms W and K may be expressed in more details as:
W
=
J
J
Pao. F ao
dt
( 4-b )
0
and
K
='2 .f
A2
1
Fao
3
dt
( 4-c)
0
where Pao' in dynes/cm 2 , and Fao' in cm 3/sec, are the aortic pressure :and
D
38.
the aortic:, flow rate respectively. ',T :'i's, the period, in seconds, of the heart
cycle.
Of course, Pao and Fao are time-dependent variables within the cycle.
In e.quation (4-c) f is the density of the fluid and for blood.r = 1.055
gm/cm3 • The cross sectional area A, in cm2 , is assumed to be constant, although variations of,·about 4 per cent have been measured in dogs' aorta
(Patel et al, 1964).
The units of power are then in ergs per second and may
be more conveniently converted to watts by use of a scale factor (107 ergs
1 watt).
=
..
In the context of the present investigation, it is useful to consider
in a series of approximately identical cycles, the average power output WO
obtained by dividing the work output per cycle by the periode
Thus, from
equation (4-a), one obtains:
( 4-d )
which is written as:
,
.....
-;-
WO = W + K
The latter equation defines two power terms, the mean rate of pressure-volume
•
•
work W and the mean rate ofkinetic energy outflow K,
and the se terms may be
computed as show,n'in (4":d) using equations (4-b) and (4-c).
Both the energy terms (4-b) and (4-c) have been defined in relation to
the pressure and flow at the left outlet of the heart, but, it is understood
that similar expressions may be written for the right outlet of the heart.
This applies also to the expressions derived below.
It is customary to evaluate the importance of the frequency dependence
of power by computing the "so called" d.c. and a.c. components.
The average
e
39.
pressure Pao and the average flow F ao being defined by:
J
1
Pao =T"
Pao
dt
( 4-f )
Fao
dt
( 4-g )
0
and
F
J
-1
ao -T
0
-;~
•
•
the relevant d.c. components Wd • c • and Kd.c. of both power terms W and K are
readily computed as:
-=
•
.
Wd.c.
Pao • F ao
and
-:;-
:;:;!
K
d.c.
2
~
-3
• ( F ao)
(
4-h
)
(
4-i
)
•
•
The corresponding a.c. components Wa • c • and Ka.c. may then be obtained by
su·btracting the d.c. components
(~quations
(4-h) and (4-i)) from the total
powerterms in (4-e), that is:
-.-
....
-Wa • c •= W •
4.2.2.
Wd.c.
-• -•
( 4-j )
( 4-k )
The freguency dependence of the hydraulic power output of the heart
This conceptual separation of the average ·power components is useful in
our problem to study the frequency dependence of hydraulic power at the·heart
outlets.
On the one hand, it is specified that both the average aortic flow
and pressure are kept constant, hence, the corresponding d_c. components of
40.
the power output expressed by equations (4-h) and '4-j) are also kept constant.
On the other hand, the heart in pumping appropriate stroke volumes, as the
frequency of contraction is varied, produces different pressure and flow
waves.
The corresponding variations of the total power output (equation 4-e)
are therefore attributed to the frequency-dependent a.c. power components (4-j)
and (4-k).
The constraints of the problem concern only the left side of the heart.
However, provided that the pulmonary vascular bed resistance does not vary,
it may be assumed, on the basis of the systemes dynamics (see p. 17) that the
mean pulmonary arterial pressure is relatively constant, following the maintenance of a constant mean aortic pressure level.
Consequently, the similar
considerations may be made concerning the hydraulic power output of the right
ventricle.
Typical data on the hydraulic power output of a doges heart beating in
the specified conditions of our problem are now presented.
The data concer-
ning the right ventricular power output have been obtained from Milno.r et al,
(1966).
These authors have used a partly theoretical partly experimental
approach in deriving the power components associated with the pressure-volume
work.
Their method involves in particular the impedance of the pulmonary
vascular bed and the harmonie content of the Ïlow pulse at different heart
frequencies.
We have used O'Rourke's data (1967), to derive the corresponding
terms at the left ventricular outlet of the heart (see Appendix 1).
Only
partial results are available for the kinetic energy outflow rate and these
are discussed separately later on.
The data shown in Table 4-1 have been computed assuming a cardiac output of 2.5 liters per minute delivered into both the pulmonary and systemic
41.
vascular beds at mean pressure of 20 and 100 mm.Hg respectively,
In these
conditions, theleft ventricle delivers 0,555 watt compared to 0,111 watt for
-,-
the right ventricle when considering only the d,c, components Wd,c, of the mean
rates of pressure-volume work.
~
The associated a,c. components Wa.c, are·
frequency-dependent and decrease from 0.124 to 0.074 watt at the entrance of
the aorta and from 0,135 to 0,030 watt at the entrance of the pulmonary artery
when the heart frequency increases from 60 to 160 beats per minute (1,0 to 2,6
cps)o
The combined right and left a,c. power components represent 28% of the
overall total at 60 beats per minute and only 13% at 160 beats per minute.
TABLE 4,1
PRESSURE-VOWME WORK: P(MER FREQUENCY DEPENDENCE
Left Ventricle
Right Ventricle
Left + Right
~
..
- Left + Right
,
i
.-
Wac + Wdc
,
:f
,
60
.124
,135
.259
.925
90
,098
.075
,173
.839
120
~079
,050
,129
.795
160
,074
.030
,104
.770
= heart rate in beat per minute
Wa,c o = a.c. power associated with
f
T'
pressure-volume work in watt
The kinetic energy outflow rate
t~~!'p:r:essure".power
content.
at both the
heart
outle~differs
from
both in magnitude and in the relative a 1 c, and d.c,
In the above case, the cross sectional areas of the pulmonary trunk
and of the aorta have been taken as 1,2 and 1.0 cm2 respective1y.
Then, the
42.
values of the d.c. components of the kinetic energy outflow rates are 0.0037
and 0.OD25 watt at the left and right ventricular outlets respectively.
Furthermore~
Milnor's data indicate that the corresponding a.c. component on
the right side of the heart drops from 0.035 to 0.002 watt when the heart
rate increases from 60 to 160 beats per minute.
On the left side of the heart,
a frequency dependence of the same type may be assumed to exist in view of
the fact that both ventricles eject identical average stroke volumes.
In
general, the power associated with the kinetic energy is around 2 per cent of
the total power output and the a.4wcomponents are predominant.
4.2.3.
The hydraulic power output of the heart: an unacceptable performance
criterion
One important fact emerges from the above data.
In order to satisfy
the system's presumed demands of constant mean flow and pressure, the hydraulic
power requirement is a decreasing function of the operating frequency of the
heart.
This characterizes the frequency dependence of both the power terms
associated with the kinetic energy and the pressure-volume work respectively.
This is not unexpected and it may be observed even in a simple "windkessel"
model of the system made up of a
Re parallel circuit connected to a rectangular
wave current source (Taylor, 1964).
This particular model was indeed used by
Taylor in discussing the hydraulic power output of the heart as a performance
criterion in the cardiovascular system.
This author has agreed that the heart
normally operates at rest at frequencies which are not optimum with respect to
this performance criterion.
Indeed, in minimizing its hydraulic power output,
the heart should then select high frequencies in contrast to what is seen in
vivo.
It has then been accordingly suggested that the optimization may be
carried out not in the resting state, but, at "the other end of the scale".
that is when the system is operating at peak demand, in which case, high
rates are indeed selected.
This latter proposaI however implies that the cardiovascular system is
operating non optimally during a major part of one's own life since most
activities are carried outat resting or moderately above resting levels
of cardiac output.
Furthermore, in view of the overall adaptation occurring
within the body's homeostasis systems in conditions of peak demand, it is not
obviou~
that the cardiovascular system is optimizing a performance criterion
of its own rather than an overall performance criterion such as maximum
oxygen supply.
In view of these objections, and because of the assumption
made earlier that the normal in vivo values of the operating parameters are
optimum with respect to an appropriate relevant performance criterion, we
conclu de that the hydraulic power output is unacceptable as a performance
criterion.
It may be useful to compare at this point asimilar situation in the
walking process.
Indeed, the lift power necessary to achieve a given walking
velocity rate drops by more than 50 per cent as the step frequency is increased
from 70 to 120 steps per minute (Cotes and Meade, 1960).
It would therefore
seem that the lift power should be minimized and that high step frequencies
should be selected
Q
It has however been shown that the corresponding total
rate energy expenditure or power input is a better performance criterion
since the above experimental data of Cotes and Meade reveals that this function
is minimized at the frequencies normally selected in vivo.
One may therefore
proceed to search for a performance criterion of the same nature in the
cardiovascular system.
4.3.
A new hypothesis
The following hypothesis is therefore put forwardi the cardiovascular
44.
system in pumping the cardiac output(s) at the mean arterial' pressure set by
the pressostat mechanism selects i ts operating parameters, the heart frequency
in particular, by minimizing i ts power consumption.
This may appJy only when
the system satisfies the flow demand(s) required by the on-going body activities at or around the so-called normal resting condition.
A general performance
criterion is then the power consumption per unit cardiac output.
In other
words, the system minimizes the total energy expended for every cc of blood
that has to be circulated in the vascular circuit.
According to the author's
knowledge, this proposaI for the cardiovascular system derived partly by
analogy from another system, is made for the first time.
4.4.
Review of literature on power consumption in cardiovascular system
4.4.1.
Preliminary considerations
Two essential questions must be answered before any attempt is made to
derive a significant measure of the hypothetical performance criterion.
These
concern:
a) the sites at which power is expended in the cardiovascular system,
and their relative importance in the present contexte
b) the practical measure of this power consumption.
4.4.2.
Sites of power consumption
Two dynamic effectors are present in the cardiovascular system, the
heart, the prime mover of the blood, and the smooth muscle of the blood
vessels that contract to alter the arteriolar resistance and the venous compliance.
The energy input to both these effectors is divided between their
basal metabolism assumed here to be constant and their varying requirements
for contraction.
45.
Per unit mass, the resting smooth muscle consumes around 1 cc/100 gm
weight per minute of oxygen (Kosan and Burton, 1966), compared to 1.9 (Van
Citters et al, 1957) consumed by the resting cardiac muscle.
It is however,
difficult to determine the power expended by the whole mass of smooth
muscle distributed between the arterioles and the veins.
We are more con-
cerned on the other hand with the relative changes of the contribution of
smooth muscle to the energy expenditure with changes in the systemls operating parameters.
Fortunate1y, in the present situation, a constant vasomotor
tone needs to be maintained in the arterioles to keep constant the d.c.
impedance since this constancy is specified by the conditions of our problem
(p. 29).
As to the venimotor tone, it should be reca1led that:
a) the number of smooth muscle fibers is much less in the veins than
in the arterioles
b) only small adjustment of compliance may be necessary in keeping
flow constant (see p. 33),
c) in extreme conditions of constriction of the smooth muscle, the
maximum increase in the oxygen consumption rate would be in the order of 30
per cent, according to measurements by Kosan and Burton (1966).
These factors should minimize the importance of the power component due
to variations in the venimotor tone to the extent that the overall smooth
muscle energy expenditure represent in the present problem a more or less
constant penalty not involved in the minimization of the overall system power
cost.
We are then concerned only with minimization of the power consumption
in the heart.
4.4.3.
Oxygen consumption rate: as a measure of power consumption in the
heart
In the above discussion it waspresumed that the power input to the
46.
system is measured by the oxygen consumption rate.
Indeed, the biochemical
reactions producing the energy required for both the metabolism and the
muscular contraction are oxydation processes in which oxygen must be supplied.
Hence, the power input to a metabolic process may be measured by its oxygen
consumption rate.
However, the end reaction in the energy production chain
is the conversion of ADP (adenosine diphosphate) into ATP (adenosine triphosphate), and this is done on the one part by the oxydative phosphorylation
in which oxygen is involved directly and on the other part by "anaerobic"
reactions in which oxygen is not required.
When the "anaerobic" pathway i s
utilized, an oxygen debt is incurred which however has to be fully repaid
later on in other reactions.
This situation occurs in the skeletal muscle
in particular and consequently the power consumption rate associated with a
given activity of a muscle is the one determined by the measurement of the
total oxygen consumption during both the activity and the following "recovery"
periods (S. Robinson, 1968).
Fortunately, in the heart, most of the energy
is obtained through the aerobic pathway in which the oxygen is utilized
directly.
Mommaerts and Langer (1963) have given three reasons why this
situation is favoured:
a) the cardiac muscle cells are amply supplied with mitochondria,
sites where the oxydative phosphorylation takes place.
b) the myocardium is highly vascularized and the ratio of fibers to
capillaries is 1 to 1.
c) myoglobin is present in significant quantity and provides the muscle
with an oxygen reserve to cope with any temporary decrease in the rate of
02 supply.
The possibility of anaerobic metabolic pathways cannot be excluded but
these only occur in extreme cases, and it is agreed that normally cardiac
47.
muscle does not accumulate any oxygen debt.
Therefore, in this thesis, the
power input to the heart is assumed to be appropriately measured by the
corresponding oxygen consumption rate.
4.4.4.
Relation of myocardial oxygen consumption to system's variables and
parameters
Four groups of experimental studies have been considered of importance
in this pre1iminary work.
These studies are concerned with the relation of
myocardial oxygen consumption to:
a) external work
b) deve10ped tension and related functions (as detailed below)
c) contractility, a basic controlled parameter in the heart
d) the frequency of the heart beat.
Relation of work to oxygen consumption
The ratio of the hydraulic power output of the heart and the power
input is called the efficiency.
In the case of the skeleta1 muscle, efficiency
varies with its velocity, reaching a peak maximum of about 35-43% at a
velocityof around v/b
= 0.75
(Hill, 1939).
The efficiency of the beating
heart has been studied extensive1y and the values obtained experimental1y
range from 5 to 25 per cent only.
These studies have been especia1ly con-
cerned with c1arifying the basis for the early experimenta1 observation
(Evans and Matsuoka, 1914), that any given increment of work is done more
efficiently by raising the cardiac output than by increasing arterial pressure.
Whether or not a maximum efficiency is reached at sorne pressure or flow has
not deeply concerned the physi010gists.
This is understandable because of
the 10w efficiencies prevailing anyway.
More recently, Mommaerts and Langer
(1963), proposed on the basis of both Hil1's force-velocity and velocity-
48.
efficiency relationships that a maximum efficiency should prevail in the
heart at a given load (or pressure) since load implies ve10city.
It is noted
in passing that the "pressostat" setting may then well be defined in terms
of maximum efficiency and this parameter wou1d 'be an excellent candidate as
a performance criterion in tack1ing the second problem of optimization in
CVS.
Presumab1y, the pressure setting is a1so established with appropriate
weighing of factors such as availability of flow in case of sudden increase
in demands, improved diffusion of 02, etc.
This problem cannot be however
discussed more appropriately without an extensive deve10pment outside the
scope of this thesis.
Tension and re1ated functions
The variable tension has been claimed by Sarnoff et al (1958), to be
"the main if not the sole determinant" of the myocardial oxygen consumption
rate.
These authors have advocated in particu1ar, the so-ca1led tension-time
··index TTI defined as the area under the systolic portion of the aortic
pressure Pao mu1tiplied by the heart rate HR, i.e.
P
l
TTI = HR
Pao
o
dt
( 4-1 )
where Tl corresponds approximate1y to the time of the c10sure of the aortic
valve.
Curious1y enough, the TTI index has been reported in units of mm.Hg-
sec per minute i.e., more simp1y mm.Hg.
Sarnoff et al have also pointed out
that the so defined TTI is a practica1 measure in which the pressure is
used instead of the relevant variable tension in the ventricular wa1ls.
Indeed, the latter vari able is more difficult to determine because i t requires
the measurement of the ventricular wall radius.
49.
This proposaI concerning tension has been confirmed by a great number
of studies on animaIs, (Rodbard et al, 1959; Neill et al, 1963) on isolated
hearts (Monroe and French, 1961) and also on isolated stripsof muscle
(McDonald, 1966).
There have been, however, sorne variances in the particular expression
of "index" used.
For example, a "cardiac effort" index defined by the
product of heart rate multiplied by the arterial blood pressure has been
later on proposed by Feinberg and Katz (1962) and subsequently verified by
Badeer et al (1963), Antic et al (1965).
This cardiac effort index varies
approximately in the same way as the tension-time index, and Rolett et al
(1965) have mentioned that both expressions yield a similar degree of statis-
tical significance.
Rolett also has introduced the parameter tensile stress,
namely the force per unit cross-section of the wall which then proved to be
statistically slightly better than the tension-time index.
This latter para-
meter will be of importance in the experimental part of our thesis.
Other avenues were explored.
Fron~k and Hudlickîl (965) correla.ted
oxygen consumption with the ventricular work defined as the sum of the
external stroke work and an energy component necessary to sustain pressure
at a given volume. Britman and Levine (1964), on the basis of a muscle model,
have derived the contractile element work which is made up of the fiber
shortening work plus the internaI work do ne in stretching the series elastic
component.
Results in both studies also indicate the importance of the cast
of oxygen in building up pressure or tension before any external work is
actually achieved.
In conclusion, it is generally agreed that sorne function of tension determines; myocardial oxygen uptake.
Unfortunately, critical studies to provide
50.
the appropriate formulation have not yet been made.
Contractili ty
Variations in power consumption are produced independently of the
developed tension by alterations in the cardiac contractility.
This effect
has been demonstrated by Sonnenblick, et al (1965) who origina1ly studied the
mechanical aspect of contraJility.
Such alterations are produced in vivo by
the sympathetic stimulation of the ventricles in particular and therefore,
this constitutes a new factor to be weighed in the minimization of power in
the system.
Contractility does not seem to play any significant role in the
combined adjustments of heart rate and stroke volume as discussed previously
(P. 34).
It is also known that the cardiac sympathetic nerve is silent at
rest, and becomes active only during exercise.
Since our problem does not
consider the conditions of exercise, a simplifying assumption is now made
whereby the contractility parameter is kept constant in this preliminary
analysis.
Relation to heart rate
Heart rate has been implicitly taken into account in aIl the above
quoted experiments because of the definition of the indices such as the one
given in equation (4-k).
In a number of studies, this parameter has been
specifica1ly controlled and the reported results have been carefully studied.
In Sarnoff's paper (1958), the rate is varied from 120 up to 150 while mean
aortic pressure and cardiac output were kept constant, in much the same way
as defined in our problem.
Useful indications were obtained from these data
as shown belowi however, the range of frequencies covered is limited on the
high frequency side.
Other works by Laurent et al (1956), Van Citters (1957),
51.
Berglund et al (1958), and Badeer (1963) were reviewed.
For reasons given in
the following discussion, the data from these latter works could not be used
for an appropriate evaluation of the hypothesized performance criterion.
4.4.5.
Discussion
It appears from this survey of the literature that the point of view of
most physiologists is somewhat different from the one which is our present
1
concerne
Indeed, the primary objective of these researchers has been to find
the determinants of myocardial oxygen uptake and a linear relationship has
usually been sought as evidenced by the common use of linear regression statistical methods.
Data from different animaIs have been pooled to obtain better
significance of the index at the expense of any individual characteristics.
Finally, the various hemodynamic variables are not systematically reported by
aIl the authors for each animal and in most cases only the resultant regression
equation of the selected index is available.
The information which we need
here consists of certain sets of measurements, with the necessary minimal set
of variables being:
1) the heart rate
2) the mean arterial pressure MAP
3) the cardiac output CO
4) the oxygen consumption rate.
Preferably, measurements should be carried on the same individual heart with
an adequate number of points taken over a range of frequencies from 60 to
150 beats per minute, while MAP and CO are kept constant.
data have been reported.
No such sets of
52.
Estimation of the performance criterion from the literature
In trying to compute the cost of oxygen per unit flow fIOm Sarnoff's
data, we realized that in the range of heart rate studied, an essential linear
relationship existed between the myocardial oxygen consumption per unit blood
flow, and both the heart rate and the resistance of the systemic vascular bed.
Thus,
•
( 4-m )
•
where MV0 2 is the myocardial oxygen consumption rate, CO the cardiac output,
R the resistance computed as the ratio of mean blood pressure to cardiac
output, and al' a2, a3 are constants.
Fig. 4.1 was constructed from the data of Sarnoff et al (fig. 4-a and
fig. 2-c, 1958).
To verify this relation, a multiple linear regression
analysis was performed using appropriate sets of measurements from various
sources as indicated in Table 4.2.
Appropriate corrections were made to
normalize the oxygen measurements, into the most commonly used form that is
cc 02/min/lOO gms left ventricular weight.
The coefficients of the regression
equation (4-m) were:
al
~
-7.88
a2
~
0.410
a3 = 0.137
respectively, when the cardiac output was in liters per minute, the he art
rate in beats per minute, and the resistance in mm.Hg per liter per minutes.
Both a2 and a3, the coefficients of HR and R were significant to the .001
level of probability (t
= 5.72
and 20.25 respectively, n
=87).
Thus, the
•
~
.-E .-E
1:
1:
'- '-
20
cr .-2...
UI
w::>
I-A..
< ....
01:::>
z
0-
v
0
,~c; o-~
\~\t,<,0
16
~ô\e
ô t\
zO
ou
-<
t:~~
::><
(/)u
•.$'Oj 'li'"
0-'"
~
,'li
\
~(lj
u
u
1-
•
~e;
12
a
....
Zz
w::>
C>
>-01:
4
Xw
o
A..
O~I--~--~--~--~~---r--~--T---~~---r--~--~~~ao
40
100
120
o
60
20
RESISTANCE
mmHg
liter / min
Fig. 4.1. Oxygen consumption rate per unit cardiac output as a Function oF the resistance
(arterial pressure divided by cardiac output) at constant heart rates.
Oerived From Sarnoff's data. (Am.J .Physiol. 192:148,1958)
53.
trend present in Sarnoff's data is confirmed.
TABLE 4.2.
SOURCES OF DATA FOR REGRESSION ANALYSIS ON HEART RATE. RESISTANCE AND
MYOCARDIAL OXYGEN CONSUMPTION RATE
Number of sets of data
:
Reference
Fig. 4-a and Fig. 2-c
Sarnoff et al, (958)
3
Table 1
Gregg, D.E. et al, (965)
37
Table 1
Neill et al, (963)
17
Table 1
Antic et al, (965)
12
Table 1 (Control values)
Sonnenblick et al, (965)
18
TOTAL: 87
A first conclusion may be drawn concerning the proposed performance
criterion computed from others '; data: at any given resistance, the cost of
oxygen per unit flow rate increases in proportion (approximately) to the heart
rate increase.
This conclusion is however limited to the frequency range,
approximately 100-200 beats per minute, involved in the regression analysis.
In fact, no extrapolation can be made for low heart rates because the components of pulsatile power become
4.1).
important below 100 beats per minute (Table
However, the following alternatives exist concerning the hypothetical
performance criterion at low frequencies as shown schematically in fig. 4.2:
1)
The cost of oxygen per uni t blood flow rate decreases with decreasing
frequency with or without changes in the slope of the curve but no minimum is
54.
achieved.
2)
The co st per unit l blood flow rate reaches a mi nimum and ri ses
again at very low frequencies.
In the latter case one can investigate the
components that May cause this minimum.
Cost of O2 per unit flow
From li ter atu re
Unknown
l 0
2 0
beats/min
Heart frequency
Fig 4.2.
The cost of 02 per unit flow versus heart frequency at constant
mean arterial pressure and cardiac output.
The experiment described in the next chapter is therefore aimed at
producing the data relevant for low frequencies.
In any case, it is encour-
aging to see from fig. 4.2 that in minimizing the presently hypothesized
criterion, the system selects low frequencies in accordance with the
observations made in vivo.
55,
. :. CHAP'l'ER V
THE EXPERlMENT
5.1.
Objective and conditions of the experiment
The main objective of the experiment described below is to test the
";'
hypothesis that the performance criterion relevant in the cardiovascular
system is the myocardial oxygen consumption per unit flow.
This criterion
is presumably used by the system to determine an optimum among the various
possible combinations of heart rate and stroke volume to achieve a given
cardiac output at constant pressure.
It is pertinent to recall that the minimum data required to achieve
our objective consist of sets of the following measured variables: the beat
frequency, the aortic pressure and flow at the outlet of the heart and the
myocardial oxygen consumption.
These sets have to satisfy the following
conditions:
1) the frequencies must cover a range from 60 to 160 beats per minute
2)~the
.mean pressure and mean cardiac flow rate must be kept constant
at aIl frequencies.
5.2.
Historical development
The experimental work has been done in collaboration with Dr. S. Pitzèle,
from the Department of Surgery, Royal Victoria Hospital and McGill University.
Dr. Pitzèle is currently developing preservation techniques for hearts.
The experimental set-up includes a specially designed hydraulic circuit
(Pitz~le
et al, 1968) to which the isolated hearts are connected after a
period of preservation.
With appropriate mechanical adjustments in this
56;.
circuit, the workload imposed on the heart is varied in steps up to exercise
levels in the order of 5 kg-m per minute and the myocardial metabolism
(oxygen consumption, lactate and pyruvate) under the se conditions studied.
(Pitzèle et al, in press).
The preserved hearts in this isolated system
beat at their own sinoatrial rhythm, which may vary from 110 to 130 beats
per minute.
It is very significant that this apparatus has been used not
only to test myocardial functions but also to "store" working hearts for
periods of time extendlng over 48 hours.
(Pitz~le,
personal communication).
This performance is an indication of the good matching of the circuit to the
hearts.
This set-up seemed advantageous also from our present point of view.
Indeed, the heart, in this new artificial environment is relieved from the
constraints imposed by the metabolic demands of the tissues, and furthermore
it is completely removed from both nervous and hormonal influences.
The
system is therefore uncoupled from, aIl the others as required by the assumption made previously, while still performing its usual task of circulating
the blood around a circuit.
To satisfy the objective of our experiment, the usual protocol was
modified.
The heart frequency was the main controlled parameter of the ex-
periment and to obtain low frequencies around 60 beats per minute, a surgi cal
blocking procedure was used.
The controls on the apparatus were adjusted
to maintain constant over the various selected
aortic pressure and the mean aortic flow rate.
frequencie~
both the mean
Of course, in view of the
complex dynamics of the heart, a precise adjustment to preset values of both
those controlled variables appeared to be difficult with relying only on the
visual feedback of the operator.
This difficulty was however compensated by
the skilfulness and the experience of the circuit designer in performing
57.
tests on stored hearts.
Modifications to introduce useful feedback mechan-
isms in the apparatus were considered but they could not be brought in
without jeopardizing the progress of the continuing work on preservation.
Therefore, a limited series of preliminary experiments were conducted
with the hope that they would yield the basic trend concerning the hypothesized criterion and also permit the design of an improved artificial
testing circuit.
This chapter contains a description of:
a) the apparatus
b) the surgical procedures for the isolation of the heart and production
of the block
c) the measuring techniques, i.e., acquisition of data, instrumentation,
blood gas analysis
d) data processing, and performance calculations.
5.3.
The apparatus
A diagram of the overall hydraulic circuit and controls is given in
fig. 5.1.
The main flow loop involves only the left side of the heart.
A main
blood reservoir consists of a thermostatically controlled heat exchanger in
series with a collapsible-wall silastic balloon.
This reservoir is connected
to the left atrium of the heart through a 1.25 cm diameter tubing ended with
a metal cannula.
The heart aortic arch is attached by rigid-wall tubing
to a second silastic balloon enclosed in a.pressurized air chamber.
At the
outlet of this system there is a solenoid-actuated ball valve controlled by
a pressure switch.
The pressure switch senses the intraventricular pressure
e
.. "
-:~~:<~~
.......
':,
1\
Pressurized air chamber
~
f
~
~.
I
.
,
Rot
Rotameter
F.P
Flow Probe
PS
Pressure Switch
S
Sc
Solenoid
Outlet Cross - Sectional
Area Screw Control
OXYGENATOR
1 .LjiJastic
~.
bal/oon
Heat
Exchanger
Level
adjust
Roller Pump
Fig. 5.1. Diagram of the hydraulic circuit to test the working capacity of isolated hearts.
58.
transmitted through the ventricular wall by a cannula inserted near the apex
of the heart.
The baIl valve is closed during the contraction of the heart
and opened during the relaxation.
A fine screw control permits adjustment
of the outlet cross- sectional area through which the blood is returned to the
"main" reservoir.
Since no oxygen is removed from the blood in this portion
of the circuit, it can be returned directly to the left atrium.
This part of the hydraulic circuit is so designed as to simulate within
li mi ts the "preload" and the "afterload" as normally seen by the left ventricle.
First, the filling pressure can he adjusted by raising or lowering the level
of the main reservoir with respect to the heart.
Thus, sorne control on the
end-diastolic volume of the heart is obtained by this "venous" input.
Secondly,
both the cross-sectional area of the arterial outlet and the triggering level
of the closing pressure switch may be varied in such a way that control of
"vascular" resistance is effectively achieved.
Finally, the balloon-air
chamber system plays the role of the coupling impedance between the heart and
the "arterial" circuit termination.
Thus, the left heart flow loop is directly
controllable and essentially possesses the same dynamic elements as shown in
fig. 2.3 except that the pulmonary flow loop is absent.
A secondary "supporting" flow loop is necessary to make up for the oxygen
used by the heart in pumping blood.
This loop branches off from the main
working circuit at the entrance of the coronary arteries that perfuse the
myocardium.
The deoxygenated blood empties directly from the coronary vas-
cular bed into the right atrium and enters the right ventricle.
This blood
is then pumped at low pressure (5 cm H20) by the right ventricle into a
membrane oxygenator (Crystal et al, 1964), and finally is returned to the
main pool.
The mechanical power output of the rigbt ventricle is less than
2 milliwatts in these working conditions.
It has consequently been assumed
that the right ventricle does not contribute more to the overall power expenditure than its resting basal Metabolisme
During the preliminary phase of the experiment, the left ventricle is
not developing any pressure.
Therefore, the necessary myocardial blood flow
is produced by a roller pump connected to the main reservoir.
The pump
outflow enters the aorta through the cannulated right common carotid artery
that branches off from the aortic arch.
This pump is turned off during the
tests.
5.4.
Surgical Procedure
Young adult dogs, mostly of the German Shepherd type, were anaesthetized
by intravenous administration of sodium pentothal, intubated and ventilated
with pure oxygene
Prior to the start of surgery, an intravenous drip of 200 cc
5% dextrose in saline, 250 cc low molecular weight dextran (Rheomacrodex) and
50 cc Ringer was started.
The thoracic cavity of the heart donor was opened
through a Median sternotomy and all veins and arteries leading to and from the
heart were dissected extrapericardially.
Following heparinization with sodium
heparin (600 units per kg body weight) and' ligation of the left innominate
artery, 800 ml of whole blood were withdrawn for priming the coronary circuit
of the apparatus.
The right innominate artery and the left pulmonary artery
were cannulated and connected to the circuit.
~
Then,coronary perfusion via the
We are very grateful to Dr. S. Pitzèle for his invaluable help in doing the
surgery and in "driving" the hydraulic circuit later on in the experiment.
60.
aortic arch was started simultaneously with the clamping of the aorta distal
to the left common carotid and the right pulmonary artery.
were ligated and divided.
developed
preservati~n
AlI other vessels
The above protocol was the one adopted in the
technique.
Block procedure
The purpose of the "block procedure" is to interrupt the normal pathway
conducting the sino-atrial impulse to the ventricles.
This can be achieved
best by destroydng the connection between the A-V node and the bundle of His
(fig. 2.2).
In the dog, this connecting point is located in the right auri-
cular wall, below the coronary sinus, to the right and ne'ar the center of the
tricuspid valve septal cusp (Pruett and Woods, 1967).
An incision was made
in the right auricle and then the block was produced by electrically burning
the nodal tissue (Brutsaert, 1965).
Following the block, a dissociation was
observed between the meèhanical contractions of the auricles and of the
ricles.
vent~:',
.,:', '
Also, the P waves characterizing the atrial discharge no longer
preceded the ventricular QRS complex (high amplitude spikes in fig. 5.2) as
they do in the pre-block ECG.
Instead, they occurred at variable times between
the ventricular discharges, as shown in the post-block ECG.
After the block, the ventricular basal rhythm varied between 25 and 65
beats per minute and this allowed reliable control of the heart frequency
from about 10 beats per minute above this basal rhythm.
The electrical pacing
stimulus consi sts of a 6 msec rectangular pulse of amplitude vari able between
o and 10 volts.
The pulses were taken from a stimulator controlled by a
Tektronix 161 waveform generator.
This stimulus was delivered to the heart
by a uni polar catheter electrode inserted in the right ventricle through the
right auricle.
A return electrode was fixed on the ventricular walls near
"ft ."-, V::::'· t' ~?j ~~' :?:: IW~ ~X:- H~iX ;:? ;:c '; iStl J~F EI:'lf<: ;:?~; l:i':H 17 ;j;!IiT:; :;.:':: ;> r'.~ I~ .'
I.~
" ' : ' . . : l''~~l'~ "; rj,'·c:d~~; 1~~:I::::At:~ l:li i: 12,: '7 [jH',:' ~;-:: I::::c:>~ : f~: :>:."
' ' i ..
''' ".', .:: ·:'c.-: ;:: f:P>: ':.' , \:::lrD !:,',: JO::: "'0:.: n:!f;;':: ;_. ?:: li::. ;c: j Il:} :: ',' .'.~ ~ ~,> ':' 1:; /'"
. 1 .•
I~:;::
'l.'. ~RI';;B L{ le,'
, ~,"", f~
f4, i~8.:~:t f:'4~"tiitl5 f'::I~7tii+h, ~:'1 tii~',J .:_w i+~ :"~.-., .e;.4F •. +.~< ".':
17? ~ f:'~; !~
r,
r .- , : !"" .': ';'
: "'l
:'~ Ë-ê G:::.I~.:: ;::' .: <:".; ~rr:i :i); ~:::: Li·(} 1~? 1t:? r,~ r!'" IU:::l ~f..:: mI r,:'
(:::: 11--; () ;.; f .:: (, ,U ~ W'. ::.'. :(:r 1::"';:;', :L,':i jy~; Vi t'; J:\,:Y:< r:':o, t) !--:
1;;\1::--1::'-· (:":; 1:,.:; IL: ':'::C; N/
i','
~CF:;f;: !?~It< 'r~'iJ,:::-:;''-~ ;~:,~I':"':
J\"E! tr
",: : :
.:·:r:~:; 1::::'
il-: i; ; ..
I
. -r
,C'"
: 1
" " .. ·.·1
.. ,~
" - +, .
", '!"
:
.. !~
.
"Ip ()S P- ' ~ L je K ; : : Ir .: ' .
,
::
,1.
..
'.
'.'
:
:."
;'
.:",-:
, ""1
1
. :
..... :.J
,.'
:'
Il '. Il
r" ..•~
:':
~
. ',-'
r·
..
:
-'
,
",,-
"
li. .:,
r. · .
',
".
,;
..
.....
. ;t: , ,.
..~
.... 10"
,1. .. .". .."
1.
~
<.:1 ..
1'"
,'"
,
:',
~
1""
.'
I t ' ,';'"
......
JU~ . .
JI,
.••.
:.
,
..
.
" . '.: E)P.
':, : 1/1:,":.'
:,"
····,·.s
t,:IFi J: .'.
'. ': .':. J
':':~
., ...
Fig. 5.2. Electrocardiograrns taken before and after the production of an A-V block
and during the subsequent electrical stimulation of the heart ventricie.
The arrows indicate the positions of the atrial P-waves.
61.
the apex.
Connection to the circuit
After the block, the heart frequency was kept at approximately 100
beats per minute while the heart was removed from the dog's body.
The aortic
arch and the left atrial appendage were cannulated and connected to the
hydraulic circuit.
5.5.
Measuring techniques
5.5.1.
Instrumentation
Du.ring the experiments, the aortic flow rate, the aortic pressure and
the coronary flow were monitored continuously on a Gilson pen recorder (see
fig. 5.3).
The aortic flow rate: was measured with a Doppler shift ultrasonic
flowmeter (Franklin et al, 1963 and 1966).
The flow probe with a diameter of
1.2 cm was interposed in the arterial line distal to the aortic arch (fig. 5.1).
The aortic pressure was transmitted through a hole in the wall of the flow
probe which was connected to a Statham P23Db wire strain gauge pressure transducer by a short and stiff catheter.
This transducer was hooked up to one of
the Gilson CH-65 modules on the recorder.
a rotameter (Shipley and Wilson, 1951).
The coronary flow was measured with
Whenever necessary, the signaIs were
averaged through RC circuits with a time constant of 3.7 seconds.
The three
signaIs were also registered on tape with an Ampex SP-300 analog magnetic tape
recorder along wi th the pulses of the pacemaker and the "sampling gates" for
the off line data processing.
The flow probe transducer. was calibrated with blood using a special setup.
During the experiments, electrical reference signals wi th "flow values"
of 1.5, 3.0, 6.0 and 12 li ters per minute were used"
Similarly, a !'100 mmHg"
@
~
~
Pacemaker
1"/
1
Aortic
flow
probe
.,.,.
fi
1Doppler
ITïI
~
.......
shi!!
Ultrasonic
Flowmeter
1
Pressure transducer
/
~
Coronary
flo w
probe
~I
1
-1
3-channel
PEN RECORDER
--
~
~~
liL
10 sec.
'-----il
Rota meter
1
L
t
Fig. 5.3. Block Diagram of the Measuring Instrumentation
IL
Sampling Gate
62.
reference signal was available on the pressure channel.
was checked prior to each experiment.
Thisreference signal
The rotameter output varied in a non-
linear fashion in the low flow ranges because of the particular design of the
probe.
This instrument was calibrated after each experiment with the blood
from the circuit.
Major limitations in the bandwidth of the recorded signaIs came from
the d.c. amplifiers which had their eut-off frequencies around 17 cps.
Within
this range 0-17 cps, the frequency responses of the manometer (Yanoff, 1963)
and of the ultrasonic flowmeter were estimated to be fIat.
The rotameter
flow probe however did not respond weIl to pulsatile flows, but in our case
only the average flow values were of interest.
Data acquisition
5.5.2.
The data acquisition procedure involved sampling of the performance at
discrete times rather than continuously.
Indeed, the measurement of oxygen
consumption rate required collecting blood samples that were subsequently
analysed for their oxygen content.
Because of both the amount of technical
labor and the limited facilities, no more than seven "sets of sample measurements" were obtainable per experiment.
The first sample was usually taken at a heart rate of 100 beats per
minute.
For this first data point the cardiac output and the mean blood
pressure were adjusted at levels between 2 to 3 liters per minute, and 60 to
80 mmHg respectively, depending on the heart.
These two variables were con-
tinuou sly moni tored on the Gilson recorder until a reasonable steady state
was achieved lasting approximately one minute.
The "sampling" of the perfor-
mance consisted of obtaining a high-speed recording on paper of both pulsatile
cardiac outflow rate and arterial pressure.
Simultaneously, a gate signal
63.
marker was fed into one of the channe1s of the tape unit (see fig. 5.3).
Blood samples were th en rapid1y withdrawn in duplicate from both the arterial
inf10w and the pulmonary outf10w.
Calibration signaIs were a1so recorded
fo110wing sampling.
The frequency of the next operating point was gradua11y reached in
successive steps, and the contro1s of the circuit were readjusted so that the
same ini ti al 1evels of cardiac output and mean pressure were achieved again by
the heart.
Upon comp1etion of the series of operating points, the heart was complete1y arrested with an injection of KCL.
of the left
ventric1e~.were
The total weight of the heart and
taken and the ventricu1ar muscle volume was measured.
From experiment to experiment, the time sequence of the heart frequencies
was changed to avoid any systematic effect due to unknown time and history
dependent factors of the preparation.
5.5.3.
Blood gas ana1ysis and determination of oxygen consumption rate. *
The purpose of the laboratory analysis done on both arteria1 and venDus
b100d samples is to measure their respective oxygen contents.
These measure-
ments are necessary to determine the oxygen consumption rate of the myocardium.
The method used is exp1ained in detail by Holmgren and Pernow (1959).
*
Briefly,
-- --- ------- - - - --- - - -- - - - -- - - -
We have greatly appreciated the technical assistance of Mrs. A. Pitz'éle and
Mr. S. Sze who performed the b100d gas
.aJùllyS~s'P
Mr. A.J. Nagy' s help
throughout these experiments is also acknow1edged.
64.
the major fraction of the oxygen in the blood is bound to the hemoglobin
(Hbg) in the red cells, the remaining being dissolved in the plasma.
The
-
bound 02 in volume % (cc 02 per 100 ml blood) in a given sample is the per
cent oxygen saturation multiplied by its maximum binding capacity (1.34 cc
02 per gram Hbg multiplied by the Hbg concentration in gram/lOO ml blood).
The dissolved amount of O2 in cc is estimated from the measured oxygen partial
pressure (P02 ) in the blood as:
( 5-a:)
• 0<.
P atm is the atmospheric pressure and where
0'
is the absorption coefficient,
being the quantity of gas absorbed by 1 cc of liquid at 160 mmHg.
(for blood ~
=0.0231
at 310 C). The 02 content is determined for both
arterial and venous blood samples and the difference between the two represents
the amount of oxygen removed from the blood stream by the tissues and is
usually called the arterio-venous difference (A-V dif).
The oxygen consump-
•
tion rate V02 of an organ, in our case the whole heart, can then be readily
determined i f the rate of flow through thi s organ i s known.: . The formulais;
V0
2
= 160
(A-V dif) x (Flow rate)
( 5-b )
where the A-V difference is in cc 02 per 100 cc of blood and the flow rate in
•
cc per unit time. V0 2 is then in cc 02 per unit time.
The percent saturation and the hemoglobin concentration determinations
were performed with a Beckman Spectrophotometer.
Values for the p02
and
the pH were obtained with a Micro Astrup Equipment (Radiometer, Copenhagen),
equipped with an oxygen monitor PHA928.
Those determinations were carried
out by a weIl trained laboratory technician, and required up to three hours
65.
of work after the experiment.
In Table 5.1 numerical values for the deter-
mination of the oxygen consumption rate of Point #1, Experiment #1 are given.
TABLE 5.1
BLOOD GAS ANALYSIS: SAMPlE (POINT #1. EXPERlMENT #1)
Measured parameter
Arterial
Blood sample.
Venous
Units
p O2
130
64
Percent saturation
100
71.04
Binding capaci ty
20.94
20.94
02 bound
20.94
14.86
"
0.41
0.20
"
21.35
15.06
"
02 dissolved
02 content
6.29
A-V dif.
Coronary flow rate
147.3
Oxygen consumption
rate
9.27
Temperature 370 C
Barometric pressure = 760 mmHg.
Hbg concentration
= 15.46
gms/l00 cc.
mmHg.
cc02/100 cc blood
cc02/100 cc blood
cc/min
cc 02/min
66.
5.6.
Data processing
5.6.1.
Digitizing procedure
The analog data recorded on the magnetic tape were digitized using a
Digital Equipment Corporation PDP8/S computer equipped with an AD8S analogto-digital converter and a four-channel multiplexer.
With the set-up used,
the a-d conversion was done automatically during the ten-second gate signal
recorded on the magnetic tape at the time of sampling.
The aortic pressure
and the aortic flow rate signaIs were digitized at a fixed rate of 100 cps
along with a sequence of 100 msec rectangular pulses generated by feeding the
aortic pressure derivative into a Tektronix 161 Waveform Generator (fig. 5 6).
0
This arrangement offered a convenient way of separating the ingividual contraction cycles and permitted the evaluation of the performance on a cycle to
cycle basis.
SAMPLING
GATE
..
DERIVATIVE
~
AORTI
PRESSURE-AORTI C
FLOW
CIRaJIT
l
. J -.
~
PULSE
GENERATOR
~
WAVEFORM
GIl_ATOR~
1
Program
Interrup t
MULTIPLEXER
~
A-D
CONVERTER
COMPUTER
MEMORY
/
~
PUNCH
PDP8/S
FIG. 5.6 - DATA PROCESSING FROM MAGNETIC TAPE
The coronary flow signal was digi tized separately at a slower rate (10 cps) .
but for a minimum period of 20 seconds in order to obtain a reasonable time
67.
average.
rate.
Calibration signaIs were also fed into the PDP8/S at an appropriate
The data stored in the PDP8/S memory was punched on paper tape in four
digit decimal numbers and then read into the IBM 360 disc memory from a Datacom RAX terminal, after which it was transferred on cards for batch processing.
5.6.2.
Calculations and computer programs
The above digitized data were processed on the IBM 360 Digital Computer
for the analysis of the mechanical and energetic performance of the heart.
The essential steps of the computer program developed for that purpose were
as follow:
a)
The values at 10 msec time intervals of both the aortic pressure
and aortic flow were printed after reduction of these data with the calibration
factors.
The delay introduced by sequential sampling of the multiplexer was
also corrected for.
b)
Each cycle in this sequence was an al yS,ed.
The values of the follow-
ing parameters were obtained;
1)
the cycle period T computed as T
= (n)
(0.01)
( 5-c )
when n is the number of points in the cycle.
2) the stroke volume SV computed as -
SV
=
J
Fao dt
( 5-d )
o
where Fao is the aortic flow rate.
3) both the mean aortic flow rate Fao
0,',
'.
,
..,
given by equation (4-f) and (4-g).
and mean aortic pressure Pao
68.
4) the effective resistance of the circuit computed as R
=
Pao
Fao
( 5-e )
in dyne-sec-cm- 5 (standard units) and also in mmHg per liter per minute.
5) the energy and power relations as defined in chapter IV by equations
(4-a) to (4-e) and (4-h) to (4-k) were also computed.
The various integrals
were calculated according to the simple trapezoidal rule with a time increment
of 0.01 sec.
and
Average values for aIl cycles within the sequence were obtained
subse~ently
è)
used in calculation of the performance criterion.
the determination of the tension-time index started with plotting
out an averaged pressure cycle.
The systolic interval of the presure wave
was then determined from the plot and the integral of the pressure over this
interval was obtained in a second computer rune
Typical computer outputs for sections b. and
c are given in fig. 5.4 and
fig. 5.5.
In the final portion of the program, the data for the whole experiment
were summarized together with the criteria computed from the data on the oxygen
consumption rate, as is explained later.
Other programs were also necessary
to compute the average coronary flows to perform the statistical analyses, and
to estimate the impedance of the circuit.
Details will be given wherever
necessary in the remaining part of this work.
In the next chapter, results from this experimental set-up concerning
the measured performance criterion are presented and
disc~ssed.
@
pressu r
cYC
period
72.053
1
0.490
73.214
2
0.490
73.224
3
0.490
72.576
4
0.490
73.507
5
0.490
73.347
6
0.490
73.634
7
0.490
73.719
8
0.480
73.159
ave
0.488
0.571
dey
0.004
mechanical energy output
flO\'I work
power
str vol
14.224
13.250
12.611
11.995
14.515
13.683
12.133
Il.772
13.023
1. 052
"
fl cc/s
29.057
27.069
25.762
24.504
29.653
27.953
24.786
24.549
26.666
2.069
d.c .com~onent
~
fl l/min
res s.u.--mmhg/Cl/mln)
41.329
1.743
3298.039
45.079
1.624
3597.331
47.373
1.546
3780.384
49.364
1.470
3939.255
41.315
1. 779
3296.964
43.732
1.677
3489.825
49.514
1.487
3951.195
50.048
1.473
3993.846
45.969
1. 600
3668.354
3.620
0.124
288.816
a.c component
a.c.comp
int(pr.fl) av(pr) .av(fl)
str wrk
0.672ge-Ol
0.2785e 00
0.3457e 00
0.1692e 00
1
0.7120e-Ol
0.2636e
00
0.3348e
00
0.163ge
00
2
0.7000e-Ol
0.250ge
00
0.320ge
00
0.1571e 00
3
0.6567e-01
0.2365e 00
0.3022e 00
0.147ge 00
4
0.822ge-01
0.289ge 00
0.3722e 00
0.1822e 00
5
0.7135e-01
0.2727e 00
0.3440e 00
0.1684e 00
6
O.6760e-01
0.2427e 00
0.3103e 00
0.151ge 00
7
O.6905e-01
0.2407e
00
O.3097e
00
0.1485e 00
8
0.7056e-01
0.2594e
00
0.3300e
00
0.lG11e 00
ave
O.5137e-02
0.1968e-01
0.2362e-01
dey
0.1198e-01
ktnettc energy
a.c.comp
CavCfl »**3
intCfl**3)
cyc
str k.e.
O.3602e-02
0.439ge-02
0.7972e-03
0.2154e-02
1
O.3893e-02
0.6445e-03
0.453:3e-02
0.2221e-02
2
0.3793e-02
0.5556e-03
0.4348e-02
0.2128e-02
3
O.3501e-02
0.4781e-03
O.397ge-02
0.1948e-02
4
0.5058e-02
0.8473e-03
0.5906e-02
0.2891e-02
5
O.4048e-02
0.7098e-03
0.4758e-02
0.232ge-02
6
0.3511e-02
0.4948e-03
0.4006e-02
0.1961e-02
7
0.3636e-02
0.4808e-03
0.4117e-02
0.1974e-02
8
0.3880e-02
0.G2GOe-03
0.4506e-02
0.2201e-02
ave
0.5128e-03
0.1468e-03
0.6255e-03
dey
0.3102e-03
cyc
a.c .percentage
Ofo
O.1946e 02
0.2127e 02
0.2181e 02
0.2173e 02
O.2211e 02
0.2074e 02
0.2178e 02
0.222ge 02
0.2140e 02
0.g206e 00
0.8188e 02
0.8580e 02
0.8722e 02
0.879ge 02
0.85G5e 02
0.8508e 02
0.8765e 02
0.8832e 02
0.8620e 02
0.2115e-01
Fig. 5.4. Computer output sample: heart mechanical performance during a sequence of cycles.
Units: energy in joules,power in watts.
+
fj
@
~
W
•
+
•
•
No. of Cycles: 8
•
+
XX
•
0
•
0000
XO
0
+
•
•
•
X
0
+
X
•
•
•
+
•
•
•
+
•
•
+
•
•
Peak pressure: 125 mm Hg
X
0
X
0
o
Peak flow rate: 148 cc/sec
X
o
X
0
X
0
XO
0
X
0
0
o
X
Pressure
o
0
o
X
o
0
00
00
o
o
X
X
'"
o
o
0
00
o
000
00
0000000000
+
•
"'"
"N
.•
X
X
001+
' " 1.0
• • •••
NN
X
+
X
•
•
•
X
o
+
•
X
•
•
~N '.•
•
al al
..........
ru ru+
o 0
III
X
X
X
•
X X X X X
Flow
X
x
x
x
\
xxx
x
X
X
X
xxxxxxxxx
III
Fig. 5.5 Computer output sample: averaged aortic pressure and flow waves. The integral of the pressure
between the arrows is the tension-time-index per beat.
xxx
X
XXX
69.
CHAPTER VI
RESULTS ON THE MEASURED PERFORMANCE CRlTERION
6.1.
General
A total of five experiments out of seven have been successfully com-
pleted with the set-up described in the last chapter.
In these experiments,
the heart rates have been varied from at least 80 beats per minute up to
150 and in three cases, low heart rates of 60 beats per minute were obtainable.
Data have therefore been collected in a range oCfrequencies considered to be
critical from the point of view of the hypothesized performance criterion.
In êbapter IV, it has already been inferred from others' data that at frequencies above 100 beats per minute, the myocardial oxygen consumption per unit
flow increases with increasing frequencies.
No conclusion has yet been
reached concerning this parameter at the lower frequencies and with the
present set-up, the analysis has been extended to the whole range of beat
frequencies.
In this chapter, the performance criterion is tested with the new
experimental data.
1)
The analysis is presented in three steps.
The results are discussed from the physiological point of view
and are compared with other published data.
2)
The constancy of mean aortic pressure and mean aortic flow at the
different îrequencies of stimul atio:l i s examined.
3)
The hypothetical performance criterion is evaluated and discussed.
The experimental results are introduced as is required by the discussion during the anlysis.
However, these results are given systematically
and in more detail for each experiment in Tables 6.1 to 6.5 in Appendix II.
70.
6.2.
6.2.1.
The results from physiological point of view
Preliminary remark
A significant test of the hypothetical performance criterion must be
done with normal physiological data being representative of a normal cardiovascular system.
Therefore, our data have been compared with others' data
from the points of view of a) the mechanical performance and
b) the levels of both the coronary flows and the oxygen consumption
rates.
6.2.2.
Mechanical performance
The mechanical performance has been determined from both the pressure
and the flow waves measured at the outlet of the heart connected to the artificial hydraulic circuit.
on es obtainable in vivo.
As shown in fig. 6.1 these waves are similar to the
The ranges of variation of the different parameters
derived from these two recorded variables have been summarized in Table 6.6
and compared with the ranges obtained both from right heart bypass preparations
and from unanesthetized resting dogs.
The coronary flows and oxygen consump-
tion rates have been included in this table and are discussed later on.
The only mechanical parameter ranging outside the "normal in vivo"
values is the mean "arterial" pressure. màirttained in the hydraulic circuit.
This difference may be due partly to the experimenters and partly to the hydraulic circuit.
.
Mean arterial pressures in the range of 57-76 rnmHg (excluding
experiment #1 at 46 rnmHg) may be considered as somewhat below the levels
normally seen in resting dogs or set experimentally whenever this variable is
under control.
In our case, those mean pressures have been selected to avoid
liter
min
4.5-
,"
1.5-
o . . . :. j:
\r
.:!,
. ::: • ,.. : l..
~I';(:::
I!:H:'
..
ri 1>',[ ::,. ,'
.'f .:',
\
.:, .' . . ., . . ;':.
. L·
.: ..
'.:
. , ;..~ !i '.•. :.. .l :'j !\; 1:":
0-
1\
" . "';\~ ~
::.·:;.::1:'."':
11'; 1.:;:0\.> :::':k:: ", .".'
..... , .
~
50-
~ "::If'>'::
i;
tL:!.::}1 :,': [': L
;;'.
. il'.: :','
' , : 1 : ,.' '.:
:'7 '. .' •
! .•. T.'; ""'.
: ' : ; .... . ....
".
l"
r:", ..... '0--:."
::
:
. ·1' ':..' '.
; '-1 '
. :::
!1.
., ::.,:
.
'.
"
.,
••
:
.O::.e.'
,.:1,
',1
,".:
-
,
..
.•
Lv:
'", . . . :~ Stmùli 'teld '. J.' .; , : '
.- .:.,
;":.} ..
::t-,.~
,"
':J. tn :.U Lle. ' :" ·12~1 Pit
, :1
l
.,;
; .', .-' .•••
"". ":
".1·'
"
j:
,
:' . :.
~ .. :
. 1'; .,.
',: ;'.: ,
. .-('
L
;':
:'
;:'.
. l ,.
',',.
.,:: ... -
..
'
Fig. 6. 1. Typical pressure and flow waves recorded at the time of sampling.
71.
TABlE 6,6
MECHANICAL PERFORMANCE
..
Parameter
Observed Range
Units
(1)
(2)
(3)
Present
reported
series of 5
experiments
, Body wei ght
kg
18-24
20-26
18-24
20-23
: Heart rate
beat/min
145
112-138
45-122
60-150
Mean arteri al
pressure
mmHg
88.9
73-98
87-127
46, 57-74
Sl!:stolic
Diastolic
mmHg
-
-
115/68146/103
120/5095/40
Liter/min
1.7-2.8
1.7-2,2
1,8-3.. 8
1,8-3.0
-
20.9
32-68
20-33
18,5
16-23,4
-
14-30
13,13
8.6-14.5
3.7-10
6.0-14.9
118
31-84
95-291
Cardiac
Output
Stroke-work
Tension-Time
index
gm-m
mmHg-sec
per min
Oxygen consump- cc02/100gms/min
tion rate
Coronary flow
rate
cc/min
57-157
-
(1)
Table l, Pol 128, Graham et al (967)
(2)
Table l, p. 921, Sonnenbli ok et al (1965)
(3)
p. 102, Gregg et al (1965)
72.
systematic failures due to overloading of the heart at low frequencies.
the experiment
r
In
the d.c. power level must be kept constant at all frequencies
and therefore the minimum stroke work required at 60 beats per minute is
double the one required at 120 beats per minute., Furthermore, an additional
amount of stroke work must be performed because of the increasing a.c. power
level as frequency is decreased.
In view of these increased demands for
stroke work, the pressure leve1 selected in the first experiment (46 mmHg) has
been considered as being within the working capacity of the heart in these
particular experimental conditions.
In the subsequent experiments, the operating level of pressure has been
increased and in Bxperiment #6 a 74 mmHg pressure has been maintained by the
heart in the "arteria1" hydraulic circuit.
This departure from the so-called
normal pressure taken here as 80 mmHg is only 12 and 7 per cent in Experiment
n:5 and #6 and about 20 and 30 per cent in n:4 and n:7.
Despite these lower means blood pressure, the stroke work and hydraulic
power output are well within the normal values.
The decrease in d.c. power
output corresponding to a decreased d.c. pressure level is therefore compensated by an increase in the a.c. power components.
This is indicated by the
large difference between the systolic and diastolic pressures in Table 6.6.
The ratios of the a.c. power components to the total hydraulic power output
vary from 45-35 at 60 beats per minute to 12-21 per cent at 150 beats per
minute.
These ratios may be compared to the estimate made in chapter IV
where the left ventricular a.c. power component of the pressure-volume work
decreases from 22 to 13 per cent as frequency increases from 60 to 160 beats
per minute.
This effect could not be controlled by the experimenters and it
has been explained by the difference in the input impedance of the hydraulic
73.
circuit.
As shown in Appendix l by the theoretical development of MilnŒr et
al, the input impedance of the load connected to the heart is directly involved
in the determination of the a.c. power component of the pressure-volume work.
The hydraulic impedance of the artificial circuit is grossly estimated,
later on in this thesis, and is compared to the input impedance of the aorta.
Although a difference may be observed between these impedances, its effect.on
the a.c. power components measured in the circuit cannot be quantitated from
this gross
e:s:timate~
In.practice, both the lower arterial pressures and the difference in the
impedance have to be accepted, till better data may be obtained.
On the other
hand, from the overall mechanical performance point of view, the above set of
data is certainly a physiologically acceptable "sample" of an in vivo system.
6.2.3.Coronary flows
It is also observed from Table 6.6 that the coronary flows covering a
range from 95-291 cc/min are high when compared to values
dogs.
31-84 in resting
The hearts in these cases were innervated and therefore subject to
external controls not present in our preparation.
Our coronary flow values
are in agreement with those obtained by Katz and Jochim (1945), from isolated
hearts and an even broader range of coronary flow was observed (39-392 cc/min)
by these authors.
It is outside the scope of this work to discuss thevarious
influences involved in the regulation of coronary flow such as nervous stimulation, hormones, and autoregulating mechanism •• These high coronary flows
are compensated by a narrowing of the a-v differences in the coronary blood
flow and it is assumed that the myocardium extracts oxygen from the blood
according to its metabolic requirements.
74.
However, i t has been recogni zed (Br au nwald, 1958) - "that an i solated
supported heart preparation is of greater value for determining the importance
of the hemodynamic factors influencing myocardial q02' while the in situ heart
preparation (innervated, nonisolated) has been found more reliable for estimating the importance of factors influencing coronary blood flow".
On the
basis of the above statement by these weIl known physiologists, the differences
in our coronary flows with normal in vivo values have not been considered as
of any importance in the present experimental work.
6.2.4.
Relation between 02 consumption rate and tension-time-index
The data on oxygen consumption are of most importance in the present
contexte
Since tension-time-index is generally accepted as a main determinant
of the myocardial oxygen consumption, a regression analysis has been performed
between these two variables as is usually done by other researchers.
When aIl
five experiments 'are pooled, the correlation coefficient between these two
vari ables i s only 0.196 (n
= 29)
and' sorne basi c di screpanc y i s apparent.
A
closer look at a plot of TTI versus 02 consumption (fig 6.2) reveals however
that the data of experiment #7 are obviously above aIl others.
A second
analysis has been therefore done with experiment #7 excluded and the correlation coefficient obtained is 0.682 (n
=22)
and the t value 4.173
(P<:~OOl).
In Table 6.7, the coefficients of the regression equation are compared with
the ones obtained by Rolett et al (1965) and Britman and Levine (1964) and
they are found to agree closely.
Considering the small range of variation of the tension-time-index in
our experiment compared for example to the range 1500-5000 in Britman and
Levine, the level of correlation is quite acceptable.
In reviewing experiment
#7, sorne doubts have been cast on the calibration of the rotameter concerning
v
~
~:~;!:'.(1
~
cc 02 / 100gms L.V. /min
20
18
Exp
no
1
4
5
6
16
w
t-
14
0
Z
t
v
•
•
7
<1:
0::
symbol
12
Z
o
0
ï= 10
...-----Z
~
o
::>
V)
Z
o
8
V...------z
0
0
v
v
v
6
C>
O 2 = 3.1 a +
>- 4
x
0
t tt
t
t
u
zw
Z"-- t
o
0.00250 TT 1
2
0
1
0
.5
1.0
TENSION-TIME
"1.5
INDEX
2.0
2.5
3.0
3
3.5 x 10
mm Hg-sec / min
Fig. 6.2. Tension-time -index and myocardia \ oxygen consumption rate in the reported series of experiments.
No 7 t;Xp. exc \uded from the regression .
75.
TABLE 6.7
•
THE RELATION BE1WEEN 'ŒNSION-TlME INDEX (TTI) AND OXYGEN CONSUMPTION RATE (MV02)
Regression equation
al
•
TTI
Source
a2
,
2 95
.00288
Rolett et al (1965)
4.15
.00200
Britman and Levine (965)
3.18
.00250
Pooled data #1, 4, 5, 6.
G
•
MV02 in cc 02/100 gros LV/min
TTI in mmHg-sec per minute ~
*units
commonly used by most authors.
_ ....i/i
"\
ri, . .,~
1.
the absolute flow values.
Since the experiments are later on analysed on an
individual basis rather than as a group, the relative flow changes are still
of great value in this
6.3.
experiment~
Constancy of mean arterial pressure and cardiac output
The purpose of this section is to determine if the specified conditions
or constraints of th/e optimization problem have been fulfilled.
According
to these constraints, both the mean arterial blood pressure and the cardiac
output must be kept constant as the heart frequency is varied over its range.
Fig. 6.3 shows the recordings of "experimentally identica1" mean aortic
pressures and cardiac outputs as obtained at successive operating points prior
to "sampling" in experiment #7.
From experiment to experiment, the variations
@9
.
~
~~~{~,
....
~·r
EXP. # 7
6
CPM
I.IJ
0:::
IJ..
L/MIN
6.0
3:
o...J -J.
"0
IJ..
.
0
« 0
155-T---9~___1___ 79 .. -'
125
-m.
-
,'·r-L·',lJ_.:
:\t--'
J i__ "_±... !
,;
l
,
•
r--~
tt
~~
-t
r--
_
1i~-
.-
1------',
1-
.
rr:'- . '
'--1
'j
li
1
i
,
1
h-I-i--l--f-_+-I-_-+--
r-'
;
l
i-f---i-
,
1
1
FIG.6.3
•
1.
1
.
L
'
1
I!
1.
,
J 1·-·1-~
!
1
:-
1
~~
J
1
\!
1
~
.
•••
1
1
i
+--t
'J 1t=1-~ 1 i
1
-- j
~
!
"
:! i
! -! -' -il -~
III
l--L"-'-~i-!: '--1 =J--i'--!"-Î-i~
:i -- --, ... ;---. f)'J--j--l-Tl --1 --1
~ --- 'J-' ~:··-;--I--~~r-i-
jiil-tJr-l-r+-!-·I--r-.-1
-l'
1
,1
'!
_, _
l,
1 i
1::
r-·t-&-t!--tHTI· f+-tH+th-h·l-rLt,'-i li' 1 1 .-~+I-t--r+t-fil-
-B-~
-+'+--1-i
1
···I·-- -+r-f-.,-,-....L!
:,
-'r'
'::-'-I-j-Pl~=-I
,-,!-r--I-I-·i-f.---
1
i l ! ,
-+~
"1"- -- F-.
-T
f-'- -b i.-i--~. i.~·-·l· -+-
Iii
1-;"1-
~-I-I----i--I-.J-c-- --- --.L+--+
1
:-j-" ... J-'~-::-l:':
,'1
--·-1-1-~1t.;--FF-=:+l-+ _-. -~m'iJ~-Tt
, i
"
1
l'
r-
1
: ;----r-··M~-c-·'!
iL' l
.'
!
r --Cl 1i-J-j-1
':
·--!-t--[tt_t
;-+ ! 1-1-~_,i
-1 r+_L_' r-+t+T,
1
-1--+--'1
--[-i-
1
1
I'
'1
- - -!LI,
+-- -+-,
f-f- - , f - - f-I
-1-·-, 1--.--t· nl~~r-· ,-.
'
'
-î---f'--'-'+j--- r---,t--I--l-,
hh---4-·+ IL~___
_. - -~!i
, · · · t - t r--rI' -.
1
_.. !
-r'--!-' i~J
"
l ,
1-
,--i. \'
.- -- r-f-- '•
1-1-
i-~:~r- ~~ r-r-'r---~ -~r--~tLttt ~;:~Î. ,.
;-.
TIl'
-'
.
!····I
l
-
r+i 1--'+-r_+I-'-+TT'-,- " !i 1-·-r·T+·-j,-'r:-+'-!"+-'!"T'
i , , !
1 1 1
1-· . -I-w'-·'
·1-
:-ï~';~ï~'-'-
1-
T 1
y"/!
l
1
I-I--l--+-+-J--l.-I---l..-H,--t-·-j---I-I-i ,+-I--I--+-l-l-~·--l-!-
-+-+,-l-+-,+-+--+-
0
a,"l;
:
-L':-
j :' r-f
--j--r···.--+--··
1-~-I---+--I-'I-+-!--+l11! --Tt-i-- -,1-+
1
d
«
,
,
t: .-- --
'JI
~-+ ,IIIT:p::tr~"
! ' ! ! !~I'/' - ---! --r -r
1-'---'--I--T
1
'-1--1-- ----i---~-l~'--T.l- --l--L
1
~
_~
. }~2~1
79
1
l'!
1
i 1 i1 _~_
'--L"'~'i'
I!
Il
! +_
in 1: ! 1:
e--C-~ Ld~
j 1-":-=rr- ~+L Hf~'" '---~-l -l-- - .-~--I--·i--i--±--I'--"
1
l--l-~I--l-l---\.-i-H:---I-+
50
__-+ _
,
62
1
-.-
"
1-
,
J
I - j ';'-'-'-r-l-+-"
!!
i 1
i
"-1-'
-j--H-r'-'
I.-t'-t-:.a' 1
--'-,--'-
--'-~.
1'1
1
--1-.
-i+,-
-r-.,--ti--tl-b
;
.
-l-:~j
Recording of average aortic pressure and flow at different frequencies
FREQ : frequency. CPM: cycle per minute. Ao: aortic.
Dog isolated heart. Wgt 211 gms.
76.
around a computed average of these means, range from -4 to + 12% for pressure
and from -14 to + Il per cent for f10w.
The standard deviations of these
variations computed for each experiment (see Tables 6 1 to 6.5, Appendix II)
G
vary from 4 to 10% of the mean in case of pressure, and 5 to 14% for flow.
These departures from the specified experimental conditions could not be
avoided in practice since as mentioned previously, it was technical1y difficult
to "set" with high precision, two interacting variables, at best. without the
help of automatic control devices.
Sorne compromise had to be made and the
deviations were accepted in order not to pro long the periods of adjustment.
On the other hand. it is necessary that these deviations be randomly
distributed over the experiment at different frequencies.
In fig 6.4, the
individual per cent deviations from the means have been p601ed in a plot
against frequency.
Whenever the number of measurements at any given freqÛency
is sufficiently high, the deviations are equally distributed on each side of
the mean.
This is particularly true both at 100 and 75 beats per minute,
which may be considered as the critical frequencies in these experiments
(fig 4.2).
One can therefore be reasonably certain that any systematic trend
repeating from experiment to experiment, is.not due to this inevitable random
10 per cent variation on the specified conditions.
Fortunate1y, it has been
possible to account for this experimental "noise" by an acceptable correction
factor as will be discussed in the next section.
6.4.
6.4.1.
The evaluation of the performance criterion from the experimental data
General
Because of the imposed conditions on both the cardiac output and mean
aortic pressure, the oxygen consumption as measured in these experiments is
also a measure of the hypothesized performance criterion: the oxygen consumption
RESISTANCE
+ 20
ot
v~
t
v
1
v
1
z
tZl
t
+10
CI)
z
<
w
:E
0
0::
~{~~~
LI..
-
-10
z
o
----- -
.
.
1
0
-------_
.
0
v
......
iJ
0
z
.
z
1
I~V
~I
v
IZ
1
1
.
-
l
1
t
v
I?
t
.
0
<
>
ARTERIAL PRESSURE
t
w
Cl
-
CAR DIAC OUTPUT
t
1
0
:E
1t
'1
-20
0
·0
+10
v
.....
zw
z
U
0::
w
0..
-10
1
60
100
HEART
140
180
fREQUENCY
beats /min
Fig.6.4. Percent deviations From constant mean pressure,mean Flow and
resistance(d.c. impedance).
77.
per unit flow.
The measured oxygen consumption rate has been therefore
plotted as a function of heart rate in fig 6.5 and the experimental points
are fitted approximately by straight line segments.
A definite
systemati~
trend can te observed for at least four out of fi ve experiments: namely, as
frequency decreases from higher rates around 150 the oxygen consumption rate.
also decreases, as expected from previous data; however, it levels off below
100 beats per minute and even rises in at least one case (experiment #6).
In
or der to explore in detail the consequences of this interesting trend, a more
critical evaluation of the hypothetical performance criterion has to be made
from these data.
The effects of two factors have been estimated, namely - the
basal metabolism and the deviations from the specified conditions of the
experiment.
From the "improved" data, a mathematical expression of the per-
formance criterion has been used to derive the optimum heart frequency.
~
~
6.4.2.
Basal metabolism
In computing the criterion value, the constant fraction representing the
basal metabolism of the heart has been subtracted from the total 02 consumption before dividing by the actual cardiac output.
In terms of an equation,
this may be written as:
•
P.C.
= MV02CO-
BM
( 6-a )
•
where P.C. is the performance criterion, MV02 the total measured oxygen
consumption rate in the heart. BM the basal met aboli sm. 'arid :CQ the cardiac
output~
The basal metabolism has been estimated as 2.0 cc per 100 grams of
total heart weight, and in general it is an important fraction of about 20
to 40% of the total oxygen consumption rate.
This correction for metabolism has been included to obtain a criterion
c
E
'-
~
~~tr
>
-'
VI
E
12
Cl
0
0
Z
0
'N
0
10
u
u
0
9
8
z
w
/
1 z
t-
<
a:
Z
0
t~
:E
~
14
V)
~'i!
;if~!:!
....
~,.
Z
0
U
Z
w
12
C>
~
X
0
10
8
6 ----~----r_--~--_r~_.----r_--~--~--~----~--_r---100
120
140
160
80
60
beats /min
HEART
RA TE
Fig. 6.5 .
Toto 1 oxygen consumption rate as a function of heart rate (raw data).
7~.
based only upon the varying fractions of the total cost of oxygen in the heart.
6.'1.3.
Correction for the effect of deviations from the problem constraints
Equation (6-a) takes into account the effects on the measured oxygen
consumption rate due to the variations around the mean of the measured cardiac
outputs at the various
fre~encies.
Indeed, each value of the oxygen consump-
tion is divided by Hs corresponding cardiac output.
The errors due to the
variations around the mean pressure setting have been estimated and corrected
as explained in detail below.
A correction factor may be derived by considering the cardiac effort
index verified by many researchers and comparing favorably weIl with the
tension-time index (P. 48, Chapter IV).
The intercept in the regression
equation of this cardiac effort index is often considered as an estimate of
the resting metabolism.
Thus, one may wri te thi s equ ation as:
•
BR.MBP
•
where MV02 and BM have been defined previously.
( 6-b )
MBP is the mean arterial
blood pressure, BR the heart rate, and al the regression coefficient.
An
expression for the performance criterion is obtained from equations (6-a) and
(6-b).
First, equation (6-b) is divided by CO, yielding •
MV02 - BM
CO
= al
• BR.
MBP
CO
( 6-c )
which is written as:
PC
= al
• BR • R
( 6-d )
using equation (6-a). R is the resistance, defined in the usual way as MBP/CO.
79.
Considering a hypothetical case, where the performance criterion is
obtained from the same heart at a given frequency HRl but at two different
values Ra and Rb of the resistance not too far from each other, - then, one
may wri te:
( 6-e )
and
where a and b are subscripts to denote these two situations.
From the equat-
ions (6-e) and (6-f), the measure of the performance criterion PCb at point b
may be expressed in terms of the measure of the performance criterion PC a
at point a.
Thus,
( 6-g )
In correcting for the deviations fram a constant mean pressure in a given
experiment, this reasoning is applied to the ensemble of data points.
For each operating point i, the corrected criterion value is:
PCci = PCmi
•
!!.i.
( 6-h )
R·l
where PC ci is the corrected value, PCmi is the value obtadned by the measure•
ments of MV0 2f and CO in equation (6-a). Rs is the.resistance obtained by
averaging the resistances of aU operating points..
Using equation (6-a).
equation (6-h) may be written as -
= ~V02
[
CO
-
BM] i
•
~
R·l
( 6-i )
This latter expression is indeed the same as equation (6-a) but multiplied
by a correction factor, being the ratio of the "average resistance" to the
80.
particular resi stance of the point i.
The value of the cri terion has been
computed from experimental data using equation (6-0.
A typical effect of the correction as applied to experiment #1, is
illustrated in fig 6 6 in which both corrected and non corrected points are
0
shown.
In genera1, the overal1 effect is to reduce the dispersion and to
clearly demonstrate that the modified criterion passes through a minimum
value at frequencies between 100 and 70 beats per minute o
ca~culated
The values of the
criterionwith and without correction are tabulated in the tables
6.1 to 6.5 in the Appendix II.
From fig 6,4 in which the per cent deviations of the individual Ri
from the means Rs were plotted against frequency, it is observed that most
modifications are of the order of 5 to 10 per cent and also that they are
distributed evenly on either side of the means at any given frequency.
Therefore, these corrections are not
systematica~ly
applied in one or in the
other direction at any given frequency.
.\. *
TABLE 6,8
POLYNOMIAL REGRESSION ANALYSIS (n - 2)
Experiment
Number
*
-C2
2Ca
Cl
C2
C3
Variance
Ratio
1
4.15
-0.0423
+0.000194
516
F1,2
= 198.5 < .005
5
4.44
-0.0568
+0.000343
17.88
F1,"4
= 12.21
<.025
83
6
10.95
-0.169
+0.000780
14.68
F1,3
= 10.12 < .05
106
Pertains to equation (6-j) 1 p. 81.
F
P
109
OXYGEN
11
CONSUMPTIONRATE
#
Exp
1
cc O 2 / min
x : measured
10
9
x
x
1
x
8
PXYGEN
3.0
CONSUMPTION
RATE per UNIT
CARDIAC
OUTPUT
cc02/min
1iter /min
'-r,,'),o'
0
z
2.0
~z
0 ____ •
_0
z
J
1.0
z=[ x - basal metabolism
[
flow
o = z corrected for deviations from constant
mean pressure'
O~---r--~---'r---r---'----r--~---'r---r---~---r---80
120
60
100
140
160
H EART
RATE
Fig.6.6. Evaluation of the criterion from experimental data.
beats/min
81.
6.4.4.
Polynomial regression and
~ivation
of the optimum freguency
Despite the improvement obtained by applying the above justified
corrections to the raw data, the number of points in each experiment is
insufficient to indicate clearly the location of the minimum by simple
inspection of the plotted data.
methods have been used.
In this respect, standard statistical
It appeared reasonable to represent the data by a
quadratic equation of the form:
PC
=Cl
+ C2 • HR + C3 • HR 2
( 6-j )
where PC is the performance criterion* in cc 02 per 100 gms left ventricular
weight per liter of blood flow, HR is the heart rate in beats per minute, and
Cl. C2 and C3 are coefficients obtained by polynomial regression analysis.
These latter coefficients are different for each experiment and they are
given in Table 6.8 together with the statistical parameters of the regression.
The statistical significance of the quadratic term in the corresponding
regression equations is tested by the analysis of variance done on both the
linear and the linear plus quadratic regressions as is. explained by Bennett
and Franklin (1954).
The variance ratio in Table 6.8 is the critical para-
meter determining-the significance of the quadratic regression and the
probability level is determined from the tables of the F-distribution.
Des-
pite the small number of points, the quadratic term is significant in experiments number 1, 5 and 6.
It is obvious that in the case of experiment #4,
a straight line is the best curve.
Also, the points in #7 experiment cannot
be significantly fitted by polynomials of low order (n <:3) and no other
type of fit was attempted." in .this case.
In fig 6.7, the regression equations have been plotted together with
* normalized
@
'"t~~i
t-
e.t-.
:::,)
:::,)
0
u
e(
cc 02/min
lit/mTn
RATE of MYOCARDIAL
OXYGEN CONSUMPTION
per UNIT of CARDIAC OUTPUT
as a function of
7.
HEART
RATE
Cl
c:::
oC(
~
La.I
t-
e:(
c:::
z
5.
0
t-
ee...
~
:::)
en
z
0
u
z
3.
expt no
Q,1
La.I
c:.!J
>><
0
z
60
90
120
HEART
RATE
FIG.6.7
150
beats/min
~
~
82.
the experimenta11y derived values of the criterion.
The data of both experi-
ments #4 and #7 have been fitted by straight line segments.
The fo1lowing remarks may be made concerning the curves of fig 6.7
1) if on1y the range 100-150 beats per minute is considered, the
performance cri te ri on varies in proportion with the heart rate.
Furthermore,
if the points obtained around 120 and 150 beats per minute are joined by
straight line. segments in Experiments #1, 5 and 6, the slopes of these 1ines
are .016, .042 and .065 CC02/liter/beat per minute respectively.· To these
increasing slopes correspond the increasing resistances in the hydraulic circuit of 15, 26 and 39 mmHg per liter per minute respectively.
These data are
therefore in agreement with the relation derived in chapter IV;from other researchers' works in which an approximately linear relation exists between the
hypothesized criterion and both the resistance and heart rate.
2) when however the lower range of frequencies is considered, the performance cri terion does not follow any more the above pattern.
In fact, in
four out of five cases, the performance criterion is minimized at sorne frequency
between 70 and 110 beats per minute.
The particular frequency at the minimum
point defines the "optimum" frequency.
The optimum frequency is derived in experiment #1, 5, and 6 from the
ratio of the linear to the quadratic coefficients of the regression equation 6-j
as:
HI\nin
=
- C
-·2
2
C3
( 6';k )
The computed values of the optimum frequency in these three experiments
are also given in Table 6.8: In experiment #7, the optimum frequency is best
estimated as 'the frequency at the observed;minimum, i.e. 79 beats per minute.
In the case of #4, heart rates lower than 75 beats per minute were not
*
page 80
83.
obtainable and therefore, one can only say that if there is a minimum, it is
lower (or equal) to the lowest frequency achieved.
In the next paragraphs,
these optimum frequencies are discussed in more detail.
A trend: the relation between the heart size and its optimum freguency
It is observed that the optimum frequency in Table 6.8 is different for
each heart.· In trying to explain this fact, it has been noted that an approximately inverse:relationship exists between the frequency at minimum oxygen
consumption per unit flow and the weight of the heart.
Table 6.9.
This is illustrated in
Such a result, perhaps unexpected to emerge from.such a small
group of experiments, is however not an unlikely feature of the cardiovascular
system.
An interesting observation has been made in
athletes that the "type
of training" may influence the pulse rate at rest.· In particular, submaximal
exercises of the endurance type seem to have more effect in slowing down the
resting pulse th an maximal exercises of the sprint type.
This is shown in
Table 6.10 where the average resting pulse rate of sprinters is compared with
the ones of middle-distance and of long dist,ance runners.
Other studies have
been made in which measurements of the heart volume have been obtained from
similar groups of runners, Table 6.11.
When these results7from two sources
are compared, a relation seems to exist for human between the size of the heart
and its optimum resting frequencyo
The bigger the heart is, the slower the
pulse frequency is.
For: the first time., the above relation between the size and the optimum
frequency has been derived from a direct measurement of the performance on a
series of hearts stimulated over varying frequencies.
This particular trend
has made itself evident by casting data into a form of a performance criterion
proposed initially as a pure "hypothesis", and is therefore providing strong
84.
support in its favor,
It also illustrates the valuable and often unexpected
side products of a theoretical framework in which to examine data.
TABLE 6.9
RELATION HEART SIZE AND OPTlMUM* FREQUENCY
Experiment Number
Optimum frequency
(beats per min)
1
Heart weight Optimum frequency x
(gm.)
:H:eart weight:
gm per min 104
109
170
1.85
106
163
1.73
5
83
186
1.54
7
79
211
1.66
4
75 **
245
1.84
6
..
* Optimum frequency defined as the frequency at minimum oxygen consumption
rate per unit cardiac output.
** 75 was the lowest rate obtainab1e in this experiment.
TABLE 6,10
PULSE RATE IN OLYMPIe ATHLETES*
Average resting Typical range or
pulse rate
pulse rate
Sprinters (100-200 meters)
65
58-76
Middle distance runners (400·800 meters)
63
49-76
Long distance runners (1500-10,000 meters)
61
46-64
Marathon runners
58
50-67
* From
Karpovich (965) after Bramwell and Ellis.
85.
TABLE 6.11
HEART VOLUMES OF VARIOUS TYPES OF ATHLETES*
Volume ml m2 Body Surface
Sprinters
350
Middle distance runners
460
Long distance runners
600
* From Jokl (1964) after Mellerowicz.
Discussion
A positive result has been obtained in t'esting a hypothetical cri te ri on
with isolated hearts connected to an artificial circuit: a minimum power consumption per unit flow prevails at sorne value of thefrequency.
As a consequence
of this finding, one needs to define the component(s) involved in the minimization of:the total cost,' AIso, an evaluation of this experiment would not be
complete without characterizing more precisely the nature of the artificial
circuit to which the hearts were connected.
cussed in the next chapter.
These two questions will be dis-
As already mentioned, the essential result of this
experiment may already be observed in fig 6.5.
The trend existing in this raw
dataîhas been shown not to be the result of the experimental "setting" errors
which were inevitable.
The data has been refined on the basis of weIl estab-
lished experimental facts and the same correction was applied to all points.
Sorne degree of arbitrariness may be involved in fitting the points to polynomials instead of other possible mathematical functions, and this may have
influenced to sorne extent the position of the derived minima.
these are well accepted functions and methods.
Nevertheless
The resulting relationship
86.
between heart size and the optimum frequency has to be considered then as a
trend to be confirmed by further experimentation.
It is however extremely
encouraging that a 'comparison of this sort can be made at this stage of our
investigation.
Summarizing the results of this chapter 1)
Despite technical difficulties, a suitable experimental measure of
the performance criterion was obtained
2)
In four out of five experiments, a minimum value of the criterion is
present at frequencies between 70 and 100 beats per minute.
3)
The optimum frequencies are in inverse relation to heart size in
accordance wi th a well known established fact.
87.
CHAPTER VII
OPTIMIZATI ON OF P<MER CONSUMPTION IN THE CARDIOVASCULAR SYSTEM:
OF THE OXYGEN COST
7.1.
THE COMPONENTS
General
Up to now in this thesis, we have been concerned with obtaining suitable
data which have confirmed the first hypothesis suggested, that power, or
oxygen consumption, is minimized at frequencies observable in the in vivo
resting system.
Thus, while further experimental work is needed to provide
more extensive data with an improved experimental set-up, we may also enter
into a new phase of this investigation.
This phase consists in discovering by
the analysis of the system's dynamics:
a) what are the componentsof the total energy co st constituting the
performance criterion, and
b) how do these components impose varying penalties that result in a
minimum cost at a particularcombination of the system's operating parameters.
Obviously, this analysis for the cardiovascular system mus t first be
made with reference to the experimental set-up from which the essential preliminary data have been obtained.
The results may then be transposed to the
in vivo system with due considerations given to the experimental differences
in the factors involved in the optimization scheme.
In this chapter, we present a complementary discussion of our experimental
work concerning this aspect of optimization:
a) the analysis is started by the identification of two components
associated with oxygen costs
b) one of these cûmpûnents is the hydraulic power output.
This latter
88.
parameter has been discussed earlier in the evaluation of the mechanical performance of the "blocked" hearts.
Here we are interested in the variation of
hydraulic power with heart rate.
c) the other component is associated with tensile stress, and a parti':"
cular development is necessary to evaluate this parameter from our data as a
function of heart rate.
d) both the above components are discussed from the point of view of
their relative roles in the minimization ofoxygen consumption.
e) a gross estimate of the impedance of the hydraulic circuit is made,
and this completes analysis of our experimental work.
7.2.
Components of the oxygen costs
Obviously, the analysis is dependent in our case on the identification of
the components (or determinants) of the oxygen consumption .in the heart.
Des-
pite the large number of studies on the myocardial oxygen consumption in
relation to such parameters as work, tension, heart rate and contractility, etc.
a theoretical reference frame is not yat available for a quantitative discussion
of these components and only a sbnplified analysis is made here.
One may start by considering the case of the heart pumping against an
infinite resistance.
In this situation, so-called isovolumic contractions are
produced during which the outlet valves of the heart remain closed throughout
the cycle.
Since there is no outflow, the hydraulic power output is zero.
However, depending on the intraventricular volume, the contractions of the
cardiac muscle fibers generate tensions in the ventricular walls that are
associated with varying oxygen costs.
al, 1961.)
(Monroe and French, 1961; Lendrum et
This isovolumic type of contraction is however only a limiting
case of the normal he art contractions.
At normal values of the vascular bed
89.
resistance, tension is first generated "isovolumically" but thereafter and
for a major part 'ofithe contraction, this is aecompanied by the shortening of
1
the muscle fiber working against this tension to eject the stroke-volume.· Of
course, the work then done appears as both pressure-volume work and kinetic
energy at the outlet of the heart.
It is pertinent at this stage to recall the structure of the muscle as
being functionally represented by a series elastic component (SEC) in series
with a contractile component CE as shown below SEC
oo---roâ"f'----co1'---I
CE
1. . --
0
The parallel elastic component is ignored in this present discussion.
Conceptually, one may then distinguish between two different dynamic
processes in which the active CE is involved.
The CE may contract;against the
SEC, even without any·shortening of the whole fiber.
Following
ot~er
authors,
in this, we may then consider the generation of tension as the resultant of
this process.
On the other hand, it is possible for the CE to contract at
constant SEC length (isotonic), while the whole fiber shortens.
Here the
ejection of the stroke volume is the resultant of this action.
Work is done in both cases.
About 72 per cent of the contractile element
work (CEW) appears finally as fiber shortening work (FSW) in a normal
tion.
contrac~
.
However, part of this fiber shortening work (16%) is done through the
restoring elastic forces of the SEC.
About 28% of,the energy output of the
CE is thus lost and presumably, viscous components not included in the model
are responsible for these energy losseso
Since the CEW takes into account
both the external work FSW and the "internaI" work of tension generation, one
90.
should expect:that the oxygen consumption depenœclosely on this parameter.
Britman and Levine have indeed found that when CEW is used as an "index" of
the myocardial oxygen consumption, a better correlation is obtained (correlation
coefficient r
= 0.91)
th an with the usual tension-time-index (r
= 0.81).
Also, one may say that both the dynamic processes involve conceptually different oxygen costs although one cannot separate them in the normal contractions.
These considerations may justify the analysis made below in which both
the hydraulic power and tensile stress are studied with respect ta their
frequency dependence in the present optimization problem.
Hydraulic power is
directly associated with the process of the fiber shortening since the fiber
shortening work is done against the fluid inside the ventricular cavity.
On
the other hand, tensile stress, to be defined lateron, is related to the
generation of tension.
These functions are necessarily used instead of the
more appropriate energy and work functions pertaining to the cardiac fiber
muscle model itself, since these latter functions could not be obtained with
thë experimental set-up.
7.3.
Mechanical power output: freguency dependence
The total hydraulic
power output and its various components
have been computed at the outletof the left ventricle from the time course
of the pressure and flow waves as described in chapter V.
Results shown in
Tables 6.1 to 6.5 include the total hydraulic power divided into the d.c. and
a.c. components, where each of these three terms is the sum of the contribution
of both the kinetic energy and pressure-volume work.
Total hydraulic power output has been plotted against frequency for';
three typical experiments (fig 7 1).
0
Differences between experiments in the
TOTAL
HYDRAULIC
POWER OUTPUT
LEFT VE NTRICLE
watt
1.0
.8
z
v.v
y
.6
v
~ - -;xf"'-----;r;---1#~~L--- x
.4
Sc
.2
.O~---T---'----r---~--~--~---'----r---'----r---r--
60
80
100
HEART
120
RATE
140
160
beat Imin
Fig. 7.1. The total hydraulic power as a function of heart rate in three experiments.
91.
levels and the rates of change with frequency of the power of fig 7.1 are
consequent upon the different corresponding levels of pressure and flow.
In
aIl three cases, however, the total hydraulic power decreases with increasing
frequencies.
Thi s effect is present in both the power terms associ ated wi th
the kinetic energy outflow and with the rate of pressure-volume work.
In
particular, fig 7.2 shows the kinetic energy outflow rate as a function of
heart rate.
By comparison with fig 7.1, it is seen that this fraction of the
power output
~aounts
to about 3.5 to 10 per cent at 60 beats per minute.
Consequently, 90 per cent or more of the tot·al power shown in fig 7.1 is of
the pressure-volume work type.
As already mentioned, the drop in the total hydraulic power may be
attributed only to the drop in the a.c. components since, the d.c. components
are held constant when the heart rate is varied in the experiment.
This is
best illustrated in Table 7.1 where the a.c. power content of the pressurevolume work diminishes from 39 per cent down to 15 per cent when the heart
rate goes from 60-64 up to 150-163 beats per minute.
Correspondingly, the a.c,
power content of the kinetic energy outflow diminishes from 94 down to 73
per cent.
In genera1, the hydraulic power output in the experimental circuit varies
with frequency in much the same way. as it does in the normally connected left
ventricle.
The extra power required at low frequencies in the in vivo left
ventricle has been shown in chapter IV to be about 7 per cent whereas it is
about 19 per cent in this artificia1 circuit.
This significant difference is
·most likely an effect due to the difference in the input impedances of both
circuits.
We now turn to the other component, the tensile stress.
KINETIC ENERGY OUTPUT RATE
LEFT VENTRICLE
watt
.06
.04
.02
#6
*
z
v
~~.-----
-------.:.. v z
x -_ _ _ _ _ _ _- x
O.O----r--~---r--r_-~-~~--~-~----~--_r----___
60
80
100
HEART
120
140
RATE
Fig. 7.2. The kinetic energy components of the curves of fig.7.1.
160
beat /min
92.
TABlE 7.1
FREQUENCY DEPENDENCE OF THE a,c, POWER*
Heart rate
(beats per min)
Rate of pressure-volume work
(per cent a.c. content **)
Rate of kinetic energy out fION
(per 'cent a.c. content)
60-64
39
94
76-79
30
91
100-105
22
83
122-125
22
81
150-163
15
73
*
Experiments #5, 6, 7 poo1ed.
Computed as ac / (ac + dc) foreither type of power,
**
--- - - - - -- -- -- - -- -- - --- ----- - ------- -- - - 7.4.
Deve10ped tensile stress: definition and frequency dependence
7.4.1.
Pre1iminary remarks
In studying the componEmt of the oxygen cost associated wi th the gener-
ation of tension, we have first examined our data from the point of view of
the re1ationship between tension-time index and the heart rates.
As shown in
Table 7.2, this function increases with increasing frequencies (except for an
unexp1ainab1e plateau between 100 and 120 beats per minute.)
.It is pertinent to reca11 that the tension-time index, TTI, is defined
as the systolic::portion of the aortic pressure (Pao) time-integra1 (tension
-time index per stroke) multiplied by the heart rate HR -
93.
TABLE 7,2
TENSION-TlME INDEX VERSUS HEART RATE
Heart Rates
(beats per minute)
TTI*
mmHg .. sec. per minute
60-64
1630
76-80
1880
99-105
2300
122-128
2260
155-163
2750
* Averages of 5
expe~iments.
--- -- - ------- ----- - - - - ------------- --- -TTI
= HR
,',
( 7-a )
dt
o
In equation (7-a) , the time interval 0 - Tl designates the interval of
systolic contraction.
For reasons given below, the Mean systolic
is a better paramet'er than tension-time index for studying the
den ce of the component cost of the tension generation.
tensil~stress
freque~cy
depen-
We May calI this Mean
tensile stress, the Tensile Stress Index, TSI, and it May be defined on the
basis of a thin wall spherical ventricle by TSI
=llR
..
)
pv
( 7-b )
2h
o
where h is the thickness, andrm the Mean
Pv ' the intraventricular pressure.
dt
•
radiu~
of the left ventricular wall,
Of course, rm' h, and Pv are aIl functions
94.
of time.
The units of TSI are given in
mmH~sec.
per minute, the units
commonly used for TTI.
In the context of this experiment, we may note that theconstancy of
both the cardiac output and mean arterial pressure which are maintained as
the pacemaker frequency is decreased, necessarily requires increasing stroke
volumes.
In geometric terms, this means that the ventricular walls must
become considerably more distended and thin before the onset of:.systole.
This
si tuation is taken into ac'count by the tensile sU'ess index which is defined
with respect to the force per unit cross sectional area of the walls represented in equation (7-b) by the expression under the integral signe
Within
the heart cycle, this normalized force varies with time quite differently
from the pressure (Sandler and
Dodge,~
1963).
Therefore, both the tension-
time and the tensile stress indices may vary according to different functional
relations wi th the heart frequency. TSI may also be a better measure of the
oxygen requirements of the tension ',generation process as indicated by the
results of Rolett et al (1965).
It appears appropriate therefore for us to
obtain an estimate of this parameter.
7.4.2,
Estimation of the Tensile Stress Index (TSI)
The tensile stress index has been estimated from both the strOke volume
and the already computed tension-time index by a method involving successive
approximation:', of equation (7-b).
One may consider first the relations between both the mean radium r m
and the thickness h of the ventricular walls and the intraventricular volume
V, the ventricular muscle volume Vm being constant.
Continuing with the thin
wall spherical model of the left ventricle shown, as follows -
95.
Spherical
Left Ventricle
it can be shown from simple geometrical considerations that -
h
= 1.612
Fv
riri
= 0.806
[(V +
+ V )1/3 m
and that,
~m) 1/3 +
(V) 1/3J
( 7-c )
(V) 1/3]
( 7-d )
We May define the ratio of the meaQ radius to the thickness as the stress
factor SF, or more precisely,
( 7-e )
which from equations (7-c) and (7-d) May be written as -
~m)
SF
1/3 +
= 0.25
( 7-f )
1/3
In the range of volumes considered, the ratio Vm/V is usually larger
than l, thus, the equation (7-f) cannot be simplified by a series expansion.
For the limiting case V
~
7-f tends to the value 0.25.
0, the ratio Vm/V tends to infinity and equation
The stress factor has been computed as a
function of ventricular volume with values of Vm corresponding to the various
96.
sizes pertinent to our experiment (fig 7.3).
For ventricular volumes above
40 cm3 , the stress factor increases almost linearly wi th volume and steeper
slopes are associated wi th smaller hearts.
Note that at low volumes, below 10
cc, Laplace' law for thin walled sphere produces errors of 20 to 30 per cent
compared to the act"al thick walled heart (Sandler and Dodge, 1963).
Aiso
these volumes are not physiological and therefore, no particular significance
is attached to the corresponding stress factors.
An approximateexpression for the tensile stress index is obtained by
replacing the stress factor SF by its mean systolic value SF and Pv by Pao
the aortic systolic pressure in equation (7-b).
SF
= 1.Tl
~
.)
SF
Thus, we have -
dt
( 7-g )
it~;;
y
and
TSI
~
SF
•
HR.
Pao
dt
( 7-h )
0
Furthermore, when considering equation (7-a) one may write (7-h) as -
TSI
~
SF
•
TTI
( 7-i )
The mean intraventricular volume V may be written as the volume at the
end of the contraction, ESV, plus sorne fraction
f9
of the stroke volume SV:
that is,
V = ESV +
p.
SV
where SV is derived from experimental data,
(:7-j )
j9
was arbitrarily taken as
0.75 to give more weight to larger volumes since, tension is developed before
Radius
or
SF=
2.8
cm
T hic kness
Radius
2. Thickness
-3.0
2.4
Radius
2.6
2.0
2.2
1.6
1.8
1.2
1.4
.8
1.0
.4
.6
O~--~~--~----r---~----~---'r---~----r---~----~--~----~
80
100
60
o
40
20
LEFT INTRAVENTRICULAR
VOLUME
Fig. 7.3. The ratios radius/th ickness (stress factor SF) for different left ventricu lar
sizcs as functlons of the intraventricular volume. The radius and thickness
of a 100 gms left ventricle (LV) are also plotted vs the intraventricular
volume.
97.
any shortening occurs.
ESV is considered here as a parameter, of considerable
importance later on in this discussion.
It is now possible to evaluate SF from V by an addi tionaI approximation
whereby these two variables are related to each other by replacing the time
dependent variables V and SF in equation (7-f) by their time averages V and
SF respectively.
function of V.
This would be rigorously true only if SF were a linear
From fig 7.3, it is evident that in the range 10-100 cc for V,
the relation V-SF involves a "soft" : non li neari ty and the linear approximation
is not likely to introduce significant errors compared to other approximations
already made.
Table 7.3 gives the results obtained for experiment #6 for an ESV of
•
l0'cc~ :,
In particular, i t is observed that the stress factor values range
from 0.84 up to 1.04.
The tensile stress index ranges from 20.3 to 30.6 mmHg-
sec per beat and the corresponding tension-time index from 22.2 to 17.5 mmHgsec representing 33 and 20 per cent variations respectively.
This significant
difference is in fact probably underestimated in view of the many assumptions
that were necessary to derive the stress factors.
Table 7.2 shows also that the TSI per minute increases with increasing
frequency, which is the same trend already observed for the tension-time
index.
98.
TABLE 7.3
TENSILE STRESS INDEX AND TENSION TlME INDEX AT VARIOUS FREQUENCIES
.TSI,*
mmHg-sec
Stroke volume
cc
Stress Factor
TTI *
mmHg-sec
76
24.7
1.04
22.2
30.6
2329
96
19.6
0.97
20.2
25.9
2495
122
13.0
0.87
17.5
20.3
2478
163
11.1
0.84
18.5
20.8
3387
105
16.5
0.92
20.4
25.0
2630
77
21.0
0.99
22.3
29.3
2254
Heart Rate
beats per min
7.5.
"
TSI
..
mmHg-secjmin
Possible components of oxygen consumption
From an optimization viewpoint, an important feature can be pointed out
concerning those two parameters which have been discussed separately, namely,
the hydraulic power and the developed tension stress called tensile stress
index.
Both vary with frequency but in opposite directions,that is TSI in-
creases with increasing frequency whereas the hydraulicpower decreases.
It
is assumed that these functions involve separate 02 costs and therefore this
particular feature May be important in determining an optimum frequency at
which the total oxygen consumption in those experiments is minimized.
This
question is discussed:more conveniently in connection with fig 7.4 which pertains to experiment #6.
First, concerning the developed tensile stress, the effect of increasing
the parameter ESV is to shift the TSI curve upwards and to increase slightly
c
~
('II
ou
Exp. 6
u 12
z
o1-
O
10
2 consumption rate
Q..
~
:::>
en
Z
88
Z
w
9
C>
>
x
o
3
mm ~a-sec .10
min
0
0
6
8
w
-
en
1
1-
Hydraulic
Power output
w
en
w
7 en
w
0::
X
en
l-
w
.....
en
6 Z
w
1-
ew
u
Q..
59w
>
w
e
x
x
4
v
v
60
80
100
'tt EART
Fig. 7.4.
120
RATE
140
160
bea.tfmin
Possible components of the oXys'en cost at different freguencies:
the hydraulic power output and/or the developed stress area.
ESV ::end-systolic volume.
99.
the gradient with increasing
frequencies~
In this.:respect, it seems of critical
importance to know whether or not ESV is held constant during the combined
adjustments of both the stroke volume and the heart rate.
One may consider,
for example, the following hypothetical situation in which, as frequency is
decreased from say 120 down to 80 beats per minute, a concomitant upward shift
of the ESV takes place say from 10 up to 20 cc.
This ESV parameter variation
causes the actual developed tensile stress to rise at low frequencies and .:.
a minimum of the developed tensile stress is produced around 100 beats per
minute.
Thus, since oxygen is consumed in the tensile stress development, a
minimum of the latter at any given operating frequency may result in a minimum
of the oxygen consumption rate as shown in fig
7.4~
With the alternative case, in which ESV is constant or varies only
slightly, sorne other factor must explain the upward turn of the oxygen consumption rate as frequency continues to decrease.
Fig 7.4 is highly suggestive
that the hydraulic power and the developed tensile stress are then involved in
a trade-off strategy in such a way that, on the one hand, at low frequencies,
increased oxygen costs are caused by the increased::requirements of hydraulic
power whereas, on the other hand, the oxygen cost of the developed tensile
stress predominates at the high frequencies.
At sorne intermediate frequency,
the total oxygen cost of these combined components is minimum.
Unfortunately, this question cannot be answered by the present work.
It is not possible to point out which one of those alternatives, or even sorne
intermediate situâtion, pertains to these experiments, because the necessary
volume measurements are lacking.
Nevertheless, in the case where the appro-
pria te explanation for the minimum involves the hydraulic power, one still
has to account for the differences caused by the artificial impedance of the
100.
testing circuit before transposing any result to the in vivo case.
Since it
may be questioned how different from the natural impedance, this artificial
one is, we have obtained a gross estimate of this important parameter in our
experiment as shown below.
One may remark in 'closing the discussion that this analysis on the
possible components of the oxygen costs is far from being complete.
Factors
such as the cost of activation, and the viscous losses associated with shortening (Hill, 1938) have been ignored in this analysis since their impartance
in the cardiac muscle is not clearly demonstrated.
Finally, no attempt has
been made to explain the effect of size on the optimum frequency.
This prob-
lem, we feel, should also be attacked by obtaining relevant data on the
operating volume of the ventricles.
7.6. Estimation of the hydraulic input impedance of the circuit
7.6.1.
Concept of hydraulic input impedance
The concept of hydraulic input impedance has been applied to depict the
particular flow-pressure relationship at the entrance of a vessel (MacDonald,
1964).
This concept involves for its definition:the usual assumptions of
linearity and steady st.ate and the mathematical treatment is analogous to the
one used for. -; impedances in electrical and mechanical networks.
In the
particular case of the heart, considered here as a flow source, the impedance
is derived by resolving the frequency content of both the pressure pet) and
flow F( t) waves.' Convenient express ions oL.the corresponding Fourier series
are:
pet) =
*
truncated
sin (nwt + ci n)
( 7...k )
*
101.
and
F(t)=
Fn sin (nwt+ f3h·.)
where w is the fundamental angular
f~equency,
( 7-1 )
in this case, the heart rate.
Fo , •••• , Fn' and po ••••• , Pn designate the harmonie amplitude of flow and
pressure respectively, and thePn's ando(n's, the corresponding phase angles.
The impedance at the frequency nw is then a complex quantity with a modulus
Zn given by Z(nw)
and a phase angle
= Fn
Pn
Qngive~
( 7-m )
by -
Q ~ == o<..n n
( 7-n )
sets
In our experiments severaljof the fundamental frequency and related harmonies
f1
can thus be u'sed to derive the impedance.
7.'6.2.
Techniques
The set-up necessary to measure hydraulic impedance accurately is quite
involved.
Special precautions are required during these determinations such
as the careful elimination of air bubbles in the catheter-manometer system as
weIl as the calibration of the latter's dynamic response.
Furthermore, the
frequency response must be known for the overall sensor-electronics instrumentation of both flow and pressure channels.
The technical facilities available
during these experiments were not sufficient to satisfy aU these specifications
for the measurement of impedance.
It is believed however that a gross but representative estimate of the
input impedance of the "arterial" artificial circuit can be obtained up to
4 cps, that is in the region of the spectrum where the fundamental frequencies
of the normal beating heart are located.
A standard computer subroutine
102.
(FORIF) available on the IBM 360 <SSP) was used to derive the harmonic content
of each cycle.
The results on the impedance were averaged out and standard
deviations computed for any given operating point.
7.6.3.
Results
Fig 7.5 shows the modulus of the hydraulic input impedance from d.c. to
4 cps as obtained in experiment #7.
The d.c. value of the modulus agrees with-
in 1 per cent with the same parameter derived previously from the ratio of
average pressure and average flow.
0.3-0.8 x 103 dynes-sec cm- 5 range.
From 1 to 4 cps, the modulus lies in the
Similar results were consistently obtained
in five experiments, despite the variation in the d.c.modulus itself.
Phase
values are not reported since the accuracy in the setup was insufficient to"
produce confident results of this parameter o
7.\A4.
Comparison with in vivo impedance
These data on the input impedance of the hydraulic circuit used in our
experiments can now be compared with data on the input impedance of the systemic
vascular bed, i.e. at the entrence of the aorta.
the latter is shown in fig 7.5 as the dotted line.
A representative example of
The modulus of the artifi-
cial impedance does not drop as low as in the real aorta in the frequency
range from 1 to 4 cps., being generally about twice the value of the natural
impedance.
Obviously, the in vivo system has produced a better matching impedance
than the experimenter, and it is suggested that this difference may have
implications for the oxygen consumption rate.
It is evident that additional
experiments are necessary to confirm the preliminary evidence obtained with
this hydraulic circuit that a minimum power consumption per unit flow is
M
....
0
1(")
1
E
u
2.0
HYDRAULIC
INPUT
IMPEDANCE
u
Q)
11'1
1
Q)
C
>-
"C
"Arterial"
1.6
Ci rcuit
\
:1J';rl
'"
\'
en 1.2
=>
=>
~
\
- - - -
-
_ _
23 kg dog
Aorta
0
0
~
w
U
.8
Z
-<
o
W
0..
~
.4
o
"
--
........ -....... ---..
-
- .---
-
.....
_--._~
L----r------~----_,------~------r_----~------_
3
2
4
1
cps
FREQUENCY
Fig. 7.5. The modulus of the input impedance of the circuit connected to
the outlet of the left heart in the reported series of experiments .
It is compared with the input impedance of the systemic vascular
bed ofa 23 kg dog obtained by O'Rourke.( ref.,see fig.2.4)
103.
/achieved at a particular frequency.
These experiments should be performed
with the heart either in situ or connected to an improved analog of the
arterial circuit; where "improvement" relates to the impedance characteristics.
7.7.
Conclusion
In conclusion, several points of ignorance arising throughout this
analysis indicate that the problem of searching for a
su~table
performance
criterion in the cardiovascular:.system has by no means yet been completely
solved.
On the other hand, the experimental work analysed above has opened
sorne avenues for further theoretical and experimental research.
Such possi-
bilities are discussed in the next and concluding chapter, following a summary
of the main results of the present report.
lO4.
CHAPTER VIII
FUTURE WORK AND CONCLUSIONS
8.1.
General
In this concluding chapter, proposaIs are made for further work on the
optimization problem studied in this thesis, in particular that of optimization of heart rate and stroke volume in the isolated cardiovascular system.
As a starting point in the elaboration of new objectives both the theoretical
and experimental results presented in the course of this work may serve as
useful landmarks.
Therefore, it is pertinent to briefly indicate in the work
just completed 1) the contributions to the problem of optimization in the cardiovascular
system
2) the many unsolved problems and limitations of the experimental work.
8.2.
Contributions to the optimization pI'oblem
The defini tion::of the problem
While sorne cardiovascular researchers have been concerned with the optimization of structural parameters, we have rather been interested in the
optimization of the "operating" parameters.
The latter are presumably deter-
mined by an active adaptive control system.
Thus we have considered as critical
the proper definition of the problem of the heart rate-stroke volume.determination viewed through the relevant control structure.
Accordingly, the
system's;.demand is still that of the blood flow rate as achieved by the
circulation process throughout the body.
This demand is however:made under
the constraint of being delivered at constant mean arterial blood pressure.
105.
A new hypothesis
We can now tackle a properly defined problem from the point of view of
the performance criterion, namely the determination of an optimum state of the
system.
Consequently, we then propose that the cardiovascular system is
operated in such a way as to minimize the power or oxygen consumption per unit
flow demand while satisfying the pressure constraint.
New experimental data
Testing of the hypothesized criterion has necessitated the obtaining of
new experimental data.
A suitable experiment has been designed and various
techniques have been combined to measure the oxygen cost of a normally working
left ventricle (consuming a large part of the encountered cost).
This was
done over:a relatively wide range of heart rates, while satisfying the problem
constraints.
This experiment was performed with a small group of dogs' hearts
and from these data, two important preliminary conclusions have been drawn:
a) a minimum of the oxygen consumption rate is indeed obtained experimentally at rates such as normally observed in vivo.
Thus the hypothesis is
confirmed;
b) the optimum heart rates vary in inverse relation with the size of
the heart.
Here, we consider of particular significance the fact that this
trend, observed in a group of five hearts, has also been observed elsewhere
by accumulation of data on resting heart rates of a large number of athletes,
with varying heart sizes.
These contributions are reported mainly in chapter III, IV, V .and VI
respectively.
The review of the cardiovascular system presented in chapter
II is considered as an essential reference frame for the proper definition of
106.
the problem.
Chapter IV contains also a review and discussion of others' work
in the preliminary approach to the study of the performance criteria.
In
chapter VII an analysis has been attempted from our experimental data on sorne
dynamic aspects of optimization, in particular the trade off strategy between
possible components of the oxygen cost in the heart.
8.3.
Unsolved problems and limits of the experimental work
It is hoped that by summarizing sorne of the problems left unsolved and
by making realistic assessments of:',the limitations of these experiments, we
can point out the directions for further fruitful development.
We are fully aware, for example, that
~dditional
constraints may further
narrow down the range of possible solutions to the problem of heart rate-stroke
volume.
Up to now, we have considered only one of such constraints, the
maintenance of a sufficient level of arterial blood pressure.
There are other theoretical points which have not been analysedi for
example, the role of contractility, important in adaptation to exercise
speciallYi the implications of the functional structure of muscle, etc.
Aiso t
no satisfactory explanation has been developed for the indicated relation
between heart rate versus size.
Finally, in the last chapter, the analysis
of the trade off strategy has been left unresolved, whereas the effect of the
"non-optimum" artificial impedance of the testing circuit has not been
analysed quantitatively from the point of view of the possible corresponding
economical implications.
8.4.
Future work
Obviously, many of these problems. rely for their solutions on better
107.
knowledge of the system, both from the dynamics and control point of view.
When we use a perfonnance criterion such as rate of energy turnover in the
heart, then we are particularly dependent on a better understanding of the
energetics of the muscular engine than the present largely empirical knowledge
available for cardiac muscle.
Furthennore, a complete definition of the prob-
lem wi th the re levant cons t'-aints i s a maj or undertaking requiring inc reased
collaboration with medical researchers.
\
More immediat'e objectives may be fonnulated however to confinn the
evidence obtained from the preliminary experiments reported here, in particular,
that a minimum power consumption is achieved in the cardiovascular:,system. "
tH, Similar experiments are needed with appropriate modifications in the
set-up.
Also an improved arterial analog circuit :'should, be designed that
offers an input impedance close to the "in vivo" impedance.' Better control of
the specified constraints can be obtained by introducing "regulators" to keep
the variables at set values.
Also, additional measuring techniques are required
to provide data on :ïntraventricular pressure and volume.
Finally, continuous
monitoring of the oxygen consumption rate is needed since one could then
reasonably check the "steady state" hypothesis accompanying the presently-used
measuring technique.
(2)
Apart :from addi tional experimental work, further models : should be devel-
oped, in particular of the heart.
One may start from the excellent model of
Beneken (already quoted in this work). Th'e purpose is to obtain "theoretical"
results on those aspects of the dynamics that are difficult to measure experimentally.
energy
A particularly good example is the theoretical behaviour of those
and~tension
functions which cannot he simply mathematically expressed
as function of heart rate or other parameters.
It is hoped that with,the
above approach sorne light may be thrown on many aspects of the problem of the
108.
he art rate-stroke volume optimization.
Also, one May then engage with more
confidence in the other correlated aspect: namely on blood pressure optimization.
Both questions are indeed from the system's operation point of view,
a unique but complex problem 4
Conclusion
It is hoped that this work May contribute to the increasing knowledge
on the complex and highly self- adaptive cardiovascular system.
From such a
better;understanding of the relevant adaptation mechanisms, it is also hoped
that eventually one will be able to tackle more appropriately the practical
problems of treating those cardiovascular diseases that are deviations from an
optimum healthy state in this system.
109.
APPENDIX l
The following development is.due to Milnor:et al (966)0
These authors
have computed the a.c. power components of the pressure-volume work done at
the inlet of the pulmonary bed.
Their method is briefly outlined and applied
to the case of the systemic vascular bed.
At any given harmonic n of the fundamental frequency of the beating heart,
the input impedance of the vascular bed is a complex quantity defined by a
modulus Zn and a phase angle Qn (see p. 101).
If Qn is the nth harmonic of
the':input flow wave to this impedance, the corresponding real power is given
by ( A-l )
The total a.c. power is the sum over the number N of:harmonics considered;
that is -
( A-2 )
One may define Qn as a function of "th'e; mean flow rate Qo and of a
frequency dependent function Cn evaluated from experimental data.
Thus,
( A-3 )
By substitution of Equation (A-3) in (A-2) one obtains:
Cn2
( A-4 )
One may then define a ttpressure power tt coefficient G(f) such that -
( A-5 )
G(f) being determined experimentally, the aoc. power is readily computed if
110.
the mean flow rate Qo is known.
wa.c. -= l2
Q0 2 G(f)
G(f) has been evaluated for the systemic vascular impedance in a doge
The iii-phase input impedances Zn cos Qn have been obtained from fig 8, p.377,
in O'Rourke and Taylor (1967).
These data -are given in Table (A-l) for two
different fundamental frequencies •
... l.
•. __-;
TABLEA.:1
~
l
60
.08
.16 :
.22
.18
.15
.19
.24
74
.... 06
.18
.20
.15
.20
.24
.27
2
3
4
5
6
7
f
heart frequency in beat per minute
n
harmonic number
*
10 3 dynes-sec-cm- 5
The Cn values have been computed from fig 8 of the above authors .and
are listed in Table (A-2).
111.
TABLE A.2
Cn .AS A FONCTION OF FREQUENCY
~
1
2
3
4
5
6
7
60
1~84
1.66
1.33
1.06
0.72
0.41
0.16
74
1.84
1.63
1.28
0.84
0.41
0.12
0.25
Symbols f and Dl defined in Table A-l.
In Table A.3, G is given for various frequencies up.,to 186 beats per
minute.
•
The computed aGc. powerterms Wa • c • are the ones corresponding toa
cardiac output of 2.5 liters per minute (41.67 cc per sec.)
TABLE A-3
Heart rate
G
•
beats per min
dyne-sec cm- 5 x 10 3
Wa .. c •
watt
60
1.42
0.124
74
1.17
0.102
92
1.12
0.098
115
0.93
0.081
144
0.85
0.074
186
0.87
0.075
112.
APPENDIX II
TABLES OF EXPERIMENTAL R ESULTS
Definition of symbols and units.
BR'lWEI:
heart weight
gms
LVWEI:
left ventricular weight
gms
NOP:
operating point number
BR:
heart rate
beats per minute
CO:
cardiac output
liters per minute
MPB:
mean arterial blood pressure
mmHg
RI :
resistance
TTI:
tension time index
mmHg/li ter per
minute
mmHg-sec per minute
AVE:
average of aIl operating points
STDEV:
st andard devi ation
WO:
mean hydraulic power output
watt
mean d.c. component of the hydraiilic
power ou tpu t
watt
mean a.c. component of the hydraulic
power output
watt
C.F.:
coronary flow
cc/min
A-V dif:
arteriovenous difference
cc 02/100 cc blood
myocardial oxygen consumption rate
cc 02/min
-.WO •
a c .:
•
MV O·"
2"
P.C. n• c .: performance criterion (non corrected)
P.C.:
performance criterion
P.C onorm : performance criterion normalized per
100 gms left ventricular weight
cc 02/liter
cc 02;!li ter
cc 02/100gm.LVwt/Liter
113.
TABI.E 6.1
~:.~!it.
~~}
EXPERIMENT BLOCK 1
HR1WEI: 169
LVWEI:
NOP
HR
CO
MBP
RI
TTI
l
103
3.28
52.4
16.0
2025
2
129
3.26
46.3
14~2
2030
3
167
3.05
48.9
16.1
2449
4
82
2.50
45.0
18.0
1623
5
64
2.85
41,2
14.8
1450
AVE
2.99
46.8
15.8
STDEV
0.32
4.2
1.4
NOP
i./;:;:
@
100
-WO
-WO
d.c.
-WO
a.c.
1
0.489
0.401
0.089
2
0.453
0.350
0.102
3
0.403
0.341
0.062
4
0.406
0.270
0,136
5
0.525
0.303
0.222
NOP
C.F.
AV dif,
MV02
PC n • c •
1
147
6.29
9.27
1.. 89
1_87
1.87
2
169
5,07
8.59
1.69
1.89
1.89
3
152
7.04
10.73
2.52
2.47
2.47
4
188
4.63
8.69
2.26
1.99
1.99
5
291
3.99
8.99
2.087
2.23
2.23
•
PC
PC norm
114.
TABlE 6.2
EXPERIMENT BLOCK 4
HR1WEI:
245
LVWEI:
157
NOP
HR
CO
MBP
RI
TTI
1
106
2.27
64.1
29.3
2362
2
79
2.19
63.1
29.5
1973
3
123
2.40
64.0
28.0
2577
4
151
2.48
68.1
27.7
2812
2.33
64.8
28.6
0.13
2.2
0.8
•
WO d.c.
•
WO a.c.
AVE
STDEV
...
e
~.t:'
~~~',
NOP
•
WO
1
0.422
0.335
0.086
2
0.425
0.320
0.105
3
0.419
0.349
0.070
4
0.442
0.382
0.060
NOP
C.F.
A-V dif
1
206
6.85
2
186
3
4
•
. MVO
PC n• c •
PC
PC norm
14.1l
4.27
4.17
2.66
6.53
12.15
3.53
3.43
2.19
185
8.55
15.82
4.76
4.86
3.10
184
9.63
17.72
5.37
5.55
3.54
2
115.
TABlE 6,3
$i
".'.'
~
EXPERlMENT BLOCK 5
HR1WEI:
186
LVWEI:
118
NOP
1
HR
106
CO
MBP
~1
2.63
73.7
28.1
2
3
4
5
6
7
77
61
122
106
78
153
3.03
3.47
2.73
2.83
2.79
2.55
71.5
67.6
69.3
79.3
83.6
75.7
23.6
19.5
25.4
28.0
74.4
5.6
26.3
3.8
AVE
STDEV
~
WO
0.546
0.722
0.894
0.533
0.605
0.707
0.496
2096
1808
2584
2599
2355
3128
30.0
29.7
•
•
•
NOP
1
2
3
4
5
6
7
2.86
0.31
TTI
2511
WOd.c.
WO a• c •
.441
.521
.611
.431
.510
.548
.433
.106
.201
.283
.103
.094
.159
.063
•
NOP
C.F.
A-V dif
MV02
PC n• c •
PC
PCnorm
1
96
9.97
9.56
2.36
2.22
1.88
2
123
7.34
9.06
1.89
2.10
1.79
3
130
6.73
8.74
1.55
2.10
1.79
4
93
10.60
9.88
2.39
2.48
2.11
5
131
7.90
10.32
2.46
2.31
1.97
6
175
6.25
10.92
2.72
2.38
2.03
7
188
7.68
14.44
4.35
3.86
3.28
116.
TABLE 6.4
EXPERIMENT BLOCK 6
~
~.
HR1WEI:
163
LVWEI:
101
NOP
HR
CO
MBP
RI
TTI
1
77
1.90
68.4
36.1
1713
2
97
1.91
69.9
36.9
1963
3
123
1.60
66.9
41.9
2162
4
164
1.83
75.2
41.6
3037
5
106
1.75
66.3
38.5
2164
6
77
1.68
71.9
43.5
1723
1.77
0.12
69.7
3.3
39.7
3.0
AVE
STDEV
~
~.;
.
. 1T
0>
~:. Z<:
WO
•
•
WOd.c.
WOa • c •
1
2
• 430
.392
.300
.304
.. 129
.088
3
4
5
.312
.241
.070
.350
.334
.309
.262
.041
.071
6
.362
.276
.086
NOP
•
•
PCne
PC
8.35
2.85
3.10
3.08
6.10
6.10
1.66
1.77
1.75
109
6.06
6.62
2.30
2.16
2.14
4
182
6.69
12.15
5.03
4.76
4.71
5
163
4.29
7.01
2.33
2.39
2.36
6
180
4.03
7.25
2.56
2.33
2.30
NOP
C.F.
A-V dif
1
163
5.13
2
100
3
MV02
PCnorm
117.
TABLE 6.5
EXPERIMENT BLOCK 7
~
~~!!;
HR1WEI:
LVWEI:
211
128
NOP
HR
MBP
RI
TTI
1
2
126
155
2.23
2.53
56.6
55.3
"25.5
22.6
1967
2391
3
99
2.82
56.2
20.0
2040
4
5
79
63
2.36
2.75
55.9
58.4
23.8
21.3
1765
1641
6
79
2.93
56.7
19.3
1815
7
102
2.75
64.7
23.6
2172
2.62
0.26
57.7
3.2
22.3
2.2
CO
AVE
STDEV
NOP
ra
.....
WOd.c.
1
2
3
4
5
6
7
.386
.408
.546
.513
.696
.612
.545
.289
.319
.373
.317
.410
.400
.411
•
...-
WO a • c •
.097
.088
.173
.196
.286
.212
.134
"PCnc
PC
PCnorm
5.85
6.06
3.93
3.49
5.12
5.97
4.39
3.99
4.67
3.43
5.66
16.87
19.11
14.89
12.03
3.27
2.55
214
7.18
15.43
4.23
4.43
3.46
6
231
5.51
12~78
3.06
3.53
2.76
7
276
6.17
17.07
4.83
4.56
3.57
NOP
C.F.
A-V dif
1
2
3
4
180
186
170
212
9.35
10.23
8.74
5
MV02
118.
REFERENCES
1.
Antic, R., Hirsh, H.J., Katz, L.N.: The Factor Controlling Myocardia1
Oxygen Consumption per Stroke and per Minute.
Acta Cardio1. 20:310-323,
1965.
2.
Attinger, E.O.
:(editor~
"Pu1satile B100d F10w"o
McGraw Hill, New York,
1964.
3.
Aviado, D.M., Schmidt, C.F.: Reflexes from Stretch Receptors.
Physio1.
Rev. 35:247-300, 1955.
4.
Badeer, H.S.: Relative Influence of Heart Rate and Arteria1 Pressure on
Myocardial Oxygen Consumption.
Acta Cardiol. 18:356-365, 1963.
5.
Bayliss, L.E.: "Living Control Systems".
W•.H. Freeman Company, San Fran-
6.
Beneken, J.W.: A Mathematica1 Approach to the Cardiovascu1ar Function.
Report No.2-4-5-6. Institute of Medical Physics, Utrecht, Neth., 1965.
7.
Bennett,· C.A., Franklin, N.L.
the Chemica1 Industry".
8.
"Stati stical Analysi s in Chemi stry and in
John Wiley and Sons, New York, 1954.
Berg1und, E., Borst, H.G., Duff, F., Schreiner, G.L.: Effect of Heart
Rate on Cardiac Work, Myocardia1 Oxygen Consumption and Coronary B100d
Flow.
9.
Acta Physio1. Scand. 42:185-198, 1958.
Braunwald, E., Sarnoff, S.J., Case, R.B., Stainsby, W.N., Welch, G.H.,
Jr.:
Hemodynamic Determinants of Coronary Flow: Effect of Changes in
Aortic Pressure and Cardiac Output on the Relationship between Myocardial
Oxygen Consumption and Coronary Flow.
Am. J. Physio1. 192:157-163, 1958.
119.
References - cont'd
10.
Bri tman, N.A •• Levi ne, H.J.: Contractile Element Work: a Major Determinant of Myocardial Oxygen Consumption.
J. Clin. Invest. 43:1397-1408,
1964.
Il.
Brockman, S.K.: Cardiodynamics of Complete Heart Block: Reflex Control
of the Heart in Complete A-V Block.
12.
Am. J. Cardiol. 16:72-92, 1965.
Brutsaert, D.: Influence of Different Stimulation Frequencies on the
Cardiac Output at Rest and During Moderate Exercise in Dogs with Chronic
Atrioventricular Heart Block.
13.
Acta Cardiol.(Brux.) 20:469-479, 1965.
Burton, A.C. :"Physiology and Biophysics of the Circulation."Medical
Year Book Publi shers, Chic ago, 1965.
14.
Ch apman , C.B., Mitchell, J.H.: The Physiology of Exercise.
Scientific
American, 212:88-96, May 1965.
15.
Christie, R.V.: Dyspnoea in Relation to Visco-Elastic
Lung.
16.
Propp.~ties
of the
Proc. Roy. Soc. Med. 46:381-386, 1953.
Cotes,· J .E., Meade, F.: Energy Expendi ture and Energy Demand in Walking.
Ergonomies, 3(2), April 1960.
17.
Covell v J.W., Ross, J. Jr., Sonnenblick, E.H., Br au nw al d, E.: Comparison
of the Force-Velocity Relation and the Ventricular Function Curve as
Measures of the Contractile State of the Intact Heart.
Circ. Res. 19:
364-372, 1966.
18.
Cyrstal, D.K., Day, S., Wagner, C.L., Martinis, J., Owen, J., Walker,P.:
A Gravit y Flow Membrane Oxygenator.
Arch. Surg. 88:122-127, 1964.
120.
References - cont'd
19.
Donald, D.E., Shepherd, J.T.: Initial Cardi.ovascular Adjustment to
Exercise in Dogs with Chronic Cardiac Denervation.
Am. J. Physiol.
207:1325-1329, 1964.
20.
Evans, C.L., Matsuoka, y.: The Effect of Various Mechanical Conditions
on the Gaseous Metabolism and Efficiency of the Mammalian Heart.
J.
Physiol. (London) 49:378-405, 1914.
21.
Feinberg, H., Katz, L.N., Boyd, E.: Determinants of Coronary Flow and
Myocardial Oxygen Consumption.
22.
Am. J. Physiol. 202:45-52, 1962.
Forwand, S.H., McIntyre, K.M., Lipana, J.G., Levine, H.J.; Active Stiffness of the Intact Canine Left Ventricle.
23.
Circ. Res. 19:972-979, 1966.
Franklin, D.L., Schlegel, W., Watson, N.W.: Ultrasonic Doppler Shift
Blood Flowrneter: Circuitryand Practical Application, "Biomedical Sciences
Instrumentation Symposium", Plenum Press, 1963.
24.
Franklin, D.L., Watson, N.W., Pierson, K.E., and Van Citters, R.L.:
Technique for Radio Telemetry of Blood Flow Velocity from Unrestrained
AnimaIs: Amer. J. Med. Electron. 24, lst
25.
Quart~r,
1966.
Fron~k, A. 1 Hudlick~, O.: Estimation of Cardi ac Performance and Efficiency
during Aortic Conclusion and Induced Muscular Activity.
Circ. Res. 16:
545-552, 1965.
26.
Fry, D.L., Griggs, D.M.,Jr., Greenfield, J.C., Jr.: Myocardial Mechanics:
Tension-Velocity-Length Relationship of Heart Muscle.
73-85, 1964.
Circ. Res. 14:
121.
References - cont'd
27.
Ganong y W.F.: "Review of Medical Physiology".
Lange Medical Publication,
Los Altos, California, 1963.
28.
Graham, T.P., Ross, J., Jr., Cove1l,
.T~W.,
Sonnenblick,
E~H.,
Clancy, R.L.:
Myocardial Oxygen Consumption in Acute Experimental Cardiac Depression.
Circ. Res.
29.
21:123-138, 1967.
Gregg, D.E., Khouri, E.M., Rayford, C.R.: Systemic and Coronary Energetics
in the Resting Unanesthetized Dog.
30.
Circ. Res. 16:102-113, 1965.
Hill, A;V.: The Heat of Shortening and the Dynamic Constans of Muscle.
Proc. Roy. Soc. (London), Ser B, 126:135-195, 1938.
31.
Hill, A.V.: The Mechanical Efficiency of Frog's Muscle.
Proc. Roy. Soc.
(London) Ser B. 127:434-451, 1939.
32.
Holmgren, A., Pernow, B.: Spectrophotometric Measurement of Oxygen
Saturation of Blood in the Determination of Cardi ac Output: a Comparison
with the Fan Slyke Method.
Scan. J. Clin. & Lab. Invest. 11:143-149,
1959.
33.
Jolk, E.: "Heart and Sport".
Charles C. Thomas Publishers, Springfield,
Ill., 1964.
34.
Karpovich, P.V.: Physiology of Muscular Exercise, 6th ed., W.B. Saunders
Co., Philadelphia, 1965.
35.
Katz, L.N., Jochim, K.: The Control of the Coronary Flow in the Denervated Isolated Heart and Heart-Lung Preparation of the Dog.
Physiol. 143:479-494, 1945.
Am. J.
122.
References - cont'd
36.
Kosan, R.L., Burton, A.C.: Oxygen Consumption of Arteria1 Smooth Muscle
as a Function of Active Tone and Passive Stretch.
Circ. Res. 18:79-88,
1966.
37.
Laurent, D., Bolene-Williams, C., Williams, F.L., Katz, L.N.: Effects of
Heart Rate on Coronary Flow and Cardi ac Oxygen Consumption.
Am. J.
Physiol. 185:355-364, 1956.
38.
Lendrum, B., Feinberg, H., Katz, L.N.: The Oxygen Consumed and Pressure
Developed by the Dog's Left Ventricle at Different End Diastolic Volumes.
Acta Cardiol. 16:487-506, 1961 •.
39.
~
Levine, H.J., Forwand, S.A., Mclntyre, K.M., Schechter, E.: Effect of
Afterload on Force-Velocity-Relations and Contractile Element Work in the
Intact Dog Heart.
40.
Circ. Res. 18:729-744, 1966.
Levison, W.H., Barnett, G.O., Jackson, W.D.: Nonlinear Analysis of the
Baroceptor Reflex System.
41.
Circ. Res. 18:673-682, 1966.
Macdonald, D.A.: Frequency Dependence of Vascul ar Impedance in "Pulsatile
Blood Flow", editor, E.O. Atinger. McGraw Hill, New York, 1964.
42.
McDonald, R.H.: Deve10ped Tension: a Major Determinant of Myocardia1
Oxygen Consumption.
43.
Am. J. Physi01. 210:351-356, 1966.
Mi1nor, W.R •• Berge1, D.H., Bargainer, J.D.: Hydraulic Power Associated
with Pulmonary Blood Flow and its Relation to Heart Rate.
Circ. Res.
19:467-480, 1966.
44,
Milsum. J.H.: "Biological. Control Systems Ana1ysis".
York, 1966a.
McGraw Hill, New
123.
References - cont'd
45.
Milsum, J.H.: Energetic Aspects of Adaptive Biological Control.
Engineer-
ing Digest. 12(1):15-18, 1966b.
46.
Milsum, J.H.: Optimization Aspects in Biological Control Theory.
In
"Advances in Biomedical Engineering and Medical Physics", vol.I, editor,
S.N. Levine.
47.
Interscience Publishers. New York, 1968.
Mommaerts, W.H.F .M., Langer, G.A.: Fundamental Concepts of Cardi ac Dynamics
and Energetics.
48.
Ann. Rev. Med. 14:261-296, 1963.
Monroe, R.G., French, G.N.: Left Ventricular Pressure-Volume Relationships
and Myocardial Oxygen Consumption in the Iso1ated Heart.
Circ. Res. 9:
362-374, 1961.
49.
Neill, W.A., Levine, H.J., Wagman, R.J., Gorlin, R.: Left Ventricu1ar
Oxygen Utilization in Intact Dogs: Effect of Systemic Hemodynamic Factors.
Circ. Res. 12:163-169, 1963.
50.
Noble, I.M. Trenchard, D., Guz, ,A.: Left Ventricular Ejection in Conscious
Dogs: 1. Measurement and Significance of the Maximum Acceleration of Blood
from the Left Ventricle.
51.
Circ. Res. 19:139-147. 1966.
O'Rourke, M.F., Taylor, M.G.: Input Impedance of the Systemic Circulation.
Circ. Res. 20:365-379, 1967.
52.
Patel, D.J., Greenfield, JeC., Fry, D.L.: In vivo Pressure-Length-Radius
Re1ationship of Certain Blood Vessels in Man and Dog in "Pulsatile Blood
Flow", editor, E.O. Attinger, 1964.
124.
References - cont'd
53.
de Pater, L., Van Den Berg, J.W.: An Electrical Analogue of the Entire
Human Circulatory System.
54.
Pitz~le,
Med. Electron. Biol. Engng. 2:161-166, 1964.
S., Charrette, E.J.P., Dobell, A.R.C., MacLean, L.D.: Method and
Apparatus for Functional Evaluation of Isolated Hearts.
Surgery. 64:308-
314, 1968.
55.
Pi tz~le, S., Dobell, A.R.G.: in "Organ Perfusion and Preservation",
Appleton Century and Crofts, Division of Meredith Publishing Co., New
York (In press).
56.
Pruett, J.K., Woods, E.F.: Technique for Experimental Complete Heart
Block.
J. Appl. Physiol. 22:830-831, 1967.
57.
Rashevsky, N.: "Mathematical Biophysics", Dover, New York, 1960.
58.
Robinson, B.F., Epstein, S.E., Beiser, G.D., Braundwald, E.: Control of
Heart Rate by the Autonomic Nervous System.
59.
Robinson, D.A.: Quantitative Analysis of the Control of Cardiac Output
in the Isolated Left Ventricle.
60.
Circ. Res. 19:400-411, 1966.
Circ. Res. 17:207-221, 1965.
Robinson, S.: Physiology of Muscular Exercise in "Medical Physiology",
editor V.B. Mountcastle, C.V. Mosby Co., St. Louis, 1968.
61.
Rodbard, W., Williams, F., Williams, C.: The Spherical Dynamics of the
Heart, (Myocardial Tension, Oxygen, Consumption, Coronary Blood Flow
and Efficiency).
Am. Heart J. 57:348-360, 1959.
125.
References - cont'd
62.
Ro1ett, E.L., Yurchak, P.M., Hood, W.B., Gor1in, R.: Pressure-Volume
Correlates of Left Ventricular Oxygen Consumption in the Hypervolemic
Dog., Circ. Res. 17:499-518, 1965.
63.
Rosen, R,:
"Optim..:.~i ty
Principles in Biology".
Butterwotth Mathematical
Text, London, 1967.
64,
Rushmer, R.F.: Control of Cardi ac Output in "Medical Physiology and
Biophysics." Edi tor, T. Ruch and J.F. Fulton, W.B. Saunders Co., Philadelphia, 1960.
65.
Sandler, H., Dodge,
H~T.:
Left Ventricular Tension and Stress in Man.
Circ. Res, 13:91-104, 1963.
66.
Sarnoff, S.J., Braunwald, E., Welch, G.H., Case, R.B., Stainsby. W.N.,
Macruz, R.: Hemodynamic Determinants of Oxygen Consumption of the Heart
with Special Reference to Tension-Time Index.
Am. J. Physiol, 192:148-
156, 1958.
67,
Scher, A.M., Young, A.C,: Servoana1ysis of Carotid Sinus Reflex Effects
on Periphera1 Resistance.
68.
Ship1ey, R.E., Wilson, D.: An Improved Recording Rotameter.
Exp. Biol. and Med.
69.
Circ. Res. 12:152-162, 1963.
Proc. Soc.
78:724-728, 1951.
Sonnenblick, E.H.: Force-Veloci ty Relations in Mammali an Heart Muscle.
Am. J. Physiol. 202:931-939, 1962.
70.
Sonnenblick, E.H.: Series Elastic and Contractile Elements in Heart
Muscle: change in muscle 1ength.
Am. J. Physio1. 207:1330-1338, 1964.
·126.
References - cont'd
71.
Sonnenb1ick, E.H., Ross, J., Jr., Cove11, J.W., Kaiser, G.A., Braunwa1d,
E.: Velocity of Contraction as a Determinant of Myocardia1 Oxygen Consumption.
72.
Am. J. Physiol. 209:919-927, 1965.
Sonnenblick, E.H.: Determinant of Active State in Heart Muscle: Force,
Velocity, Instantaneous Muscle Length, Time.
Fed. Proc. 24:1396,1409,
1966.
73.
Taylor, M.G.: Wave Travel in Arteries and the Design of the Cardiovascular
System. In "Pulsatile Blood Flow", editor, E.O. Attinger, 1964.
74.
VanCitters,
R.L~
Ruth, W.E., Reissmann, K.R.: Effect of Heart Rate on
Oxygen Consumption of Iso1ated Dog Heart Performing no External Work.
Am. J. Physiol. 191:443-445, 1957.
~
75.
Warner, H.R.: The Frequency Dependent Nature of Blood Pressure Regulation
by the Carotid Sinus Studied with an Electric Analog.
Circ. Res. 6:35-
40, 1958.
76.
Warner, H.R., Cox, A.: A Mathematical Model of Heart Rate Control by
Sympathetic and Vagus Efferent Information.
77.
J. Appl. 17:349-355, 1962.
Wilson, T.A.: Capillary Spacing for Minimum Entropy Production.
J. Theoret •
. Biol. 11:436-445, 1966.
78.
Wilson, T.A.: Minimum Entropy Production as a Design Criterion for
Breathing. $xperientia, 20, 333, 1964.
79.
Yanoff, H.M., Rosen, A.L., McDonald, N.M., McDonald, D.A.: A Critica1
Study of the Response of Manometers to Forced Oscillations.
Biol., 8:407-422, 1963.
Phys. Med.