Download Reducing Electromagnetic Interference in DC

Reducing Electromagnetic Interference
DISSERTATION
Li
in DC-DC Converters with Chaos Control
zur Erlangung des akademischen Grades
n
Ho
ng
DOKTOR-INGENIEURIN
tio
der Fakultät für Mathematik und Informatik
Di
ss
er
ta
der FernUniversität in Hagen
von
Hong Li, M.Sc.
Changzhi/China
Hagen 2009
III
Abstract
Di
ss
er
ta
tio
n
Ho
ng
Li
Electromagnetic Interference (EMI) resulting from high rates of changes of voltage and current, impairing other devices’ performance and harming human being’s health, has become a major concern in
designing direct current (DC-DC) converters for a long time due to the increasingly wide applications
of various electrical and electronic devices in industry and daily life. Thus, the question of how to
reduce the annoying, harmful EMI has to be faced by scientists and engineers.
Normally, EMI is handled by appending a properly tuned filter to reduce it within low frequency
bands, referring to conducted EMI, or dealt with by electromagnetic shielding when it is within high
frequency bands, referring to radiated EMI. However, as a filter is restricted in a narrow frequency
band, it is not applicable to a much broader EMI frequency band alone. Therefore, multiple filters
should be employed, increasing the difficulty of design. In addition, the affixed filter circuits not only
increase cost, but also imply an increase of size and weight, rendering a product to lack portability.
Electromagnetic shielding is the process of limiting the penetration of electromagnetic fields into
a space, by blocking them with a barrier made of conductive material. Typically, it is applied to
enclosures, separating electrical devices from the ‘outside world´, and to cables, separating wires from
the environment, through which the cables run. Shielding is an effective but expensive solution for
EMI suppression. Moreover, in practice there are many leak sources on the enclosures. Therefore,
both approaches are not perfect solutions of EMI suppression.
Due to the pseudo-random and continuous spectrum characteristics of chaos, more recently the EMI
problem has been tackled by the spread spectrum approach employing chaos control. However, there
exist two prominent problems still unsolved: one is that the ripples of the output waveforms are much
bigger than those with periodically running DC-DC converters, degrading DC power supplies; and the
other one is that the parameter design of DC-DC converters becomes difficult due to the variational
frequency under chaos control. Trying to fight these two problems, this dissertation is to improve the
conventional chaos control approaches and to propose some new strategies of chaos control for EMI
suppression.
Two kinds of control approaches will be proposed in this dissertation. One is a novel chaotic peak
current mode control via parameter modulation, which cannot only reduce EMI but also suppress
output ripples easily; the other one is to combine chaos control with the most important and common
control method in DC-DC converter, i.e., pulse width modulation (PWM) control, to form a novel
chaos-based PWM control, named chaotic PWM control. This chaotic PWM control has the advantages of being easy to design, of applicability in various DC-DC converters, and of flexibility to reach
a trade-off between output ripple and EMI. Therein, the chaotic carrier plays a key rôle in generating
chaotic signals, which is designed both in digital and analogue ways, providing two alternative choices
for different applications in practice. Moreover, a chaotic soft switching PWM control is put forward,
which combines soft switching with chaotic PWM due to the fact that the soft switching technique is
to switch on and off at zero current or zero voltage to alleviate the high rates of changes of voltage
and current, to reach a better effect for EMI reduction and to reduce the power loss as well. Furthermore, the proposed EMI control approaches are simulated and implemented in hardware. The
experiments are of great significance to verify the theoretical results and simulations, especially for
future marketing.
To this end, some theoretical concerns about the calculation of the invariant density of a chaotic
mapping in a peak current mode boost converter, parameter estimation, ripple estimation, and about
stability analysis in a chaotic PWM DC-DC converter are also addressed in this dissertation, providing
theoretical explanation and verification for the simulation and experimental results, and a guideline
for systems design. Finally, one of the modern spectral estimation method, viz., the Prony method,
is employed to replace the conventional fast Fourier transform in estimating the spectra of chaotic
signals, providing more accurate results.
V
Contents
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
10
10
10
11
11
13
13
19
19
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
20
20
21
24
24
24
27
28
30
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
33
33
34
34
35
36
37
38
41
41
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
2 Chaos Control of EMI
2.1 Chaos in DC-DC Converters . . . . . . . . . . . . .
2.1.1 System Description . . . . . . . . . . . . . .
2.1.2 Experimental Observations . . . . . . . . .
2.1.3 Chaos Control . . . . . . . . . . . . . . . .
2.2 Approaches of Chaos Control for EMI Suppression
2.2.1 Chaos Control via Parameter Modulation .
2.2.2 Chaotic PWM Control . . . . . . . . . . . .
2.3 Summary . . . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3 Chaotic Peak Current Mode Boost Converters
3.1 Introduction . . . . . . . . . . . . . . . . . . . . .
3.2 Chaotic Current Mode Boost Converter Model .
3.3 Characteristics of the Chaotic Mapping . . . . .
3.3.1 Spectrum Analysis . . . . . . . . . . . . .
3.3.2 Bifurcation and Lyapunov Exponents . .
3.3.3 EMC Performance . . . . . . . . . . . . .
3.4 Experimental Verification . . . . . . . . . . . . .
3.5 Summary . . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
4 Chaotic Pulse Width Modulation
4.1 Introduction . . . . . . . . . . . . . . . . .
4.2 Design Considerations . . . . . . . . . . .
4.3 CPWM with Varying Carrier Frequencies
4.3.1 Simulations . . . . . . . . . . . . .
4.3.2 Experiments . . . . . . . . . . . .
4.4 CPWM with Varying Carrier Amplitudes
4.4.1 Simulations . . . . . . . . . . . . .
4.4.2 Experiments . . . . . . . . . . . .
4.5 Summary . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
ng
.
.
.
.
.
.
.
.
.
Di
ss
er
ta
tio
n
Ho
.
.
.
.
.
.
.
.
.
1
1
4
5
5
6
6
6
8
8
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Li
1 Introduction
1.1 EMI and EMC . . . . . . . . . . . . . . .
1.2 EMC Standards . . . . . . . . . . . . . . .
1.3 Conventional EMI Suppression Techniques
1.3.1 EMI Filtering . . . . . . . . . . . .
1.3.2 Electromagnetic Shielding . . . . .
1.3.3 Soft Switching . . . . . . . . . . .
1.3.4 Random Modulation . . . . . . . .
1.4 Motivation . . . . . . . . . . . . . . . . .
1.5 About this Dissertation . . . . . . . . . .
VI
5 Analogue Chaotic PWM
5.1 Introduction . . . . . . . . . .
5.2 Analogue Chaotic Carrier . .
5.2.1 Circuit Design . . . .
5.2.2 Chaotic Oscillator . .
5.3 Analogue Chaotic PWM . . .
5.3.1 A Boost Converter . .
5.3.2 Simulations . . . . . .
5.4 Experiments . . . . . . . . . .
5.4.1 Chua’s Diode . . . . .
5.4.2 Experimental Results
5.5 Summary . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
6 A Chaotic Soft Switching PWM Boost Converter
6.1 Introduction . . . . . . . . . . . . . . . . . . . . . . .
6.2 Circuitry and Control . . . . . . . . . . . . . . . . .
6.2.1 Circuit Description . . . . . . . . . . . . . . .
6.2.2 Chaotic Soft Switching PWM Control . . . .
6.3 Simulations and Performance Evaluation . . . . . . .
6.4 Summary . . . . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
er
ta
tio
n
7 Invariant Densities of Chaotic Mappings
7.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7.2 1-D Mapping for a Boost Converter . . . . . . . . . . . . . .
7.3 Invariant Density of a Chaotic Mapping . . . . . . . . . . . .
7.4 Eigenvector Method . . . . . . . . . . . . . . . . . . . . . . .
7.5 Invariant Density of the Boost Converter’s Chaotic Mapping
7.6 Examples of Applying Invariant Densities . . . . . . . . . . .
7.6.1 Power Spectral Density of a DC-DC Converter’s Input
7.6.2 Average Switching Frequency . . . . . . . . . . . . . .
7.6.3 Parameter Design with Invariant Density . . . . . . .
7.7 Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Di
ss
8 Stability of a Chaotic PWM Boost Converter
8.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . .
8.2 Chaotic PWM Boost Converters . . . . . . . . . . . .
8.3 Estimation of the Mean State Variables . . . . . . . .
8.4 Ripple Estimation of the Input Current . . . . . . . .
8.5 Stability . . . . . . . . . . . . . . . . . . . . . . . . . .
8.5.1 Two Operation Modes of the Boost Converter .
8.5.2 Stability . . . . . . . . . . . . . . . . . . . . . .
8.6 Summary . . . . . . . . . . . . . . . . . . . . . . . . .
9 Chaotic Spectra Analysis Using the Prony Method
9.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . .
9.2 Prony Method . . . . . . . . . . . . . . . . . . . . . .
9.3 Deriving the Power Spectral Density . . . . . . . . . .
9.4 Chaotic Spectral Estimation of DC-DC Converters . .
9.5 Summary . . . . . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
Current
. . . . .
. . . . .
. . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Li
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
ng
.
.
.
.
.
.
.
.
.
.
.
Ho
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
43
43
44
44
45
47
47
48
48
51
51
55
.
.
.
.
.
.
56
56
57
57
60
62
65
.
.
.
.
.
.
.
.
.
.
66
66
67
68
68
69
70
70
73
74
75
.
.
.
.
.
.
.
.
76
76
77
77
80
82
82
83
84
.
.
.
.
.
85
85
86
87
89
92
10 Conclusion
93
References
96
1 Introduction
1
Chapter 1
Li
Introduction
1.1
Ho
ng
With the rapid development and application of electrical and electronic devices and products,
electromagnetic interference (EMI) has become a major problem annoying scientists and engineers. What is EMI? How do people control EMI? What and how can we do to fight EMI?
These questions are to be answered first in this chapter.
EMI and EMC
Di
ss
er
ta
tio
n
The recent six decades have witnessed a rapid and tremendous advance in power electronics.
A broad range of electronic products has come forth and is widely applied in industry and
human daily life, such as computers, wireless communication devices, electrical motors, electric
vehicles and so on. Most of them, e.g., laptop computers and cellular telephones, are supplied
or charged by direct current (DC). Therefore, AC-DC and DC-DC converters are necessary to
convert the alternating current (AC) supplied out of sockets to the DC required. Thus, DCDC converters play a very important rôle in portable electronic devices, which are primarily
supplied with power from batteries. Such electronic devices often contain several subcircuits
with their own voltage requirements different to the ones provided by batteries or external
supplies. Additionally, the voltage of a battery declines as its stored power drains away. DCDC converters provide a means to maintain voltage from a partially lowered battery voltage,
thereby saving space instead of using multiple batteries to accomplish the same task.
The electrical and electronic devices that carry rapidly changing electrical currents constitute
a source of EMI, while some natural objects and phenomena, such as sun and northern lights,
are other sources as shown in Figure 1.1. EMI is an unwanted disturbance that affects electrical
circuits due to either electromagnetic conduction or electromagnetic radiation emitted from an
external source. The disturbance may interrupt, obstruct, or otherwise degrade or limit the
effective performance of circuits.
For example, we all know that the use of mobile telephones is forbidden on board of an airplane
because of possible interferences with the aircraft’s communication and navigation systems.
Recent events regarding cellular telephones include that of a Northwest Airlines flight which
was diverted because of suspicious telephone use by passengers, and a British Airways flight
that had to return to Heathrow 90 minutes after take-off, because nobody confessed to have
used a cellular telephone even though crew members heard a telephone ringing, which caused
considerable fear among passengers and crew and created severe flight delays. Two further examples are an electrical wheelchair suddenly veering due to radio and microwave transmissions,
and an infant apnea monitor failing to alarm because of the ambient electromagnetic fields
[62, 73].
In terms of frequency bands, EMI is categorised as conducted EMI and radiated EMI, which
1 Introduction
ng
Li
2
Ho
Figure 1.1: Typical electromagnetic environment
er
ta
tio
n
are illustrated in Figure 1.2. Conducted EMI is caused by the physical contact of conductors as
opposed to radiated EMI, which is caused by induction (without physical contact of conductors),
depending on the frequency of operation. That is to say, for lower frequencies EMI is caused
by conduction and, for higher frequencies, by radiation.
The conducted EMI, normally having frequencies between 10kHz and 30MHz, can be further
classified into common mode (CM) noise and differential mode (DM) noise in terms of different
directions of conduction.
Common Mode Noise is conducted through all lines in the same direction, and always exists
between any power line and ground.
Di
ss
Differential Mode Noise is conducted through all lines in inverse directions, and always
exists between power lines.
Figure 1.2: EMI coupling modes
1 Introduction
3
Di
ss
er
ta
tio
n
Ho
ng
Li
In converters, DM currents flow in and out of the power supplies via the power leads and their
sources (or loads), and are totally independent of any grounding arrangements. Consequently,
no DM current flows through the ground connections. On the other hand, CM currents flow
in the same direction either in or out of the power supplies via the power leads and return to
their sources through the lowest available impedance paths, which are invariably the ground
connections. Even if the ground connections are not deliberate, CM currents flow through
parasitical capacitors or parasitical inductors to the ground, as Figure 1.2 shows.
Empirically, at frequencies below approximately 5MHz, the noise currents tend to be predominantly DM, whereas at frequencies above 5MHz the noise currents tend to be predominantly
CM [67].
Converters also generate radiated EMI emissions normally with frequencies between 30MHz
and 1GHz. Radiated EMI appears in the form of electromagnetic waves that “radiate” into the
immediate atmosphere directly from a circuitry and its interface leads. The circuitry and its
interface leads can liken themselves to a transmitting antenna for this radiated EMI, as shown
in Figure 1.2.
Radiated EMI can contain electric and magnetic fields. The strength of the electric field
is proportional to the circuit voltage, operation frequency, and “the effective length of the
antenna”. The strength of the magnetic field is proportional to the circuit current, operation
frequency, and “the effective area of the antenna loop”. Since the circuit parameters and
operation frequency are fixed for a converter’s operation characteristics, the only variable factor
is the length of the power line, or the enclosed loop area of the power line’s return path.
Therefore, it can be seen that radiated EMI can be minimised by physically locating the noisegenerating source as close to its source and load as possible. However, mechanics rarely permit
such a compact assembly.
Normally, EMI can be estimated by measuring the power spectral density (PSD), which describes how the power of a signal or time series is distributed with frequency, such as the
example given in Figure 1.3. More information about PSD can be found in [55].
Figure 1.3: A triangle waveform and its power spectrum
According to Figure 1.3, it is obvious that the spectrum consists of the operation frequency and
its harmonics. If the harmful harmonics of input and output signals are not filtered in convert-
4
1 Introduction
ers, they can corrupt the power sources and interfere with the operation of other equipment
running from the same sources. Radiated EMI noise will also be generated and interfere with
the operation of adjacent equipment, which gives rise to important electromagnetic compatibility
(EMC) problems.
EMC is defined as the ability of an apparatus to function satisfactorily in its electromagnetic
environment without introducing intolerable electromagnetic disturbance to other apparati in
the same environment. EMC includes two issues to achieve the defined ability.
Li
Emission Emission issue is related to the unwanted generation of electromagnetic energy, and
to the countermeasures which should be taken in order to reduce such generation and to
avoid the escape of any remaining energies into the environment.
1.2
ng
Susceptibility Susceptibility or immunity issue, in contrast, refers to the correct operation of
electrical equipment in the presence of unplanned electromagnetic disturbances.
EMC Standards
tio
n
Ho
As mentioned above, power electronic devices, including converters, are of great benefit to
human beings and are widely applied in our daily life. Unfortunately, the widespread use
of power electronic products, at the same time, causes the serious EMI problem. Facing the
harmful interference, international communities have agreed on standard regulations, i.e., EMC
standards, which are supposed to ensure unimpeded systems in the electromagnetic environment
to comply with regulatory requirements. Here, some basic information on EMC standards for
converters is listed.
ss
er
ta
Generic EMC Standard A top-level standard for a type of equipment encompasses specific
basic standards in its references. The currently relevant standard for power supplies is
[ EN61204-3: 2000] . This covers the EMC requirements for power supply units with DC
output(s) of up to 200V, at power levels up to 30kW, and operating from AC or DC
source voltages of up to 600V. The abbreviation EN refers to Euro Norm or European
standard. Europe has led the field in establishing standards for EMC and many other
areas, which have been adopted worldwide with some local deviations.
Di
List of Basic Standards The relevant basic standards mentioned in EN61204-3 are: EN55022
and EN55011 for conducted and radiated electromagnetic interferences emitted by power
supplies. The FCC has set similar standards in the USA. It is expected that EN55022 will
become a worldwide standard as CISPR22. There are two levels for the emission limits,
Class A and Class B. Class B is normally required, and puts a lower limit on allowed
emissions. Particular aspects of EMC are addressed in the standard EN61000 as follows:
EN61000-4-2 Immunity to electrostatic discharge
EN61000-4-3 Immunity to radiated radio frequencies
EN61000-4-4 Immunity to fast transient voltages on input lines
EN61000-4-5 Immunity to lightning surges on input lines
EN61000-4-6 Immunity to conducted radio frequencies
EN61000-4-8 Immunity to power frequency magnetic fields
EN61000-4-11 Immunity to damage from input line voltage reductions
EN61000-3-2 Limits to the harmonic currents that can be taken from the input lines
1 Introduction
5
EN61000-3-3 Limits to the voltage fluctuations that the power supply can cause to the
line input voltage
Performance Criteria In immunity testing, there are four classes by which passing or failure
are assessed, viz., Class A: no loss of function or performance due to the testing, Class B:
temporary loss of function or performance, self-recoverable, Class C: loss of function or
performance which needs intervention to restore, and Class D: permanent loss of function
or performance due to damage, always representing a failure.
Conventional EMI Suppression Techniques
Li
1.3
EMI Filtering
tio
1.3.1
n
Ho
ng
Many methods have been proposed to suppress EMI of converters. Among them, EMI filtering
is the most common and oldest approach, which is used to reduce conducted EMI to satisfy
low-frequency EMC standards. For meeting high-frequency EMC standards, electromagnetic
shielding is usually employed, which is to reduce radiated EMI. Both methods can well suppress
EMI, but at the same time increase cost and weight, rendering products to lack portability.
In order to meet the stricter international EMC standards and the requirements for electronic
products to be lighter, smaller, and cheaper, some new EMI suppression techniques should be
proposed and field-tested, for instance, the soft switching technique and random modulation.
In the sequel, these four methods will be introduced, respectively.
Di
ss
er
ta
Converters are a source of EMI due to pulsating input currents and rapidly changing voltages
and currents [11]. An EMI filter is normally appended at the input side of a converter.
Since conducted EMI is made up of CM noise and DM noise, an EMI filter consists of two
function blocks as shown in Figure 1.4: Cx and differential choke are used to filter the DM
noise, while Cy and common choke filter the CM noise.
Figure 1.4: EMI filter
EMI filters are effective to suppress conducted EMI for converters, but also have some shortcomings, for instance, their volume is too huge for some products, not only the noise but also the
useful signals may be suppressed, and any EMI filter is designed for a special narrow frequency
band, only, unable to work on the entire broad frequency band.
6
1 Introduction
1.3.2
Electromagnetic Shielding
n
Ho
ng
Li
Electromagnetic shielding is the process of limiting the penetration of electromagnetic fields
into a space, by blocking them with a barrier made of conductive material as shown in Figure 1.5. Typically, it is applied to enclosures, separating electrical devices from the ‘outside
world´, and to cables, separating wires from the environment the cables run through. Electromagnetic shielding used to block radio-frequency electromagnetic radiation is also known as RF
(Radio Frequency, about 3KHz to 300GHz) shielding. It is worth to notice that electromagnetic
shielding is an effective but expensive solution for suppressing EMI. On the other hand, there
may exist many leak sources, such as intake, display window, socket in real shield, degrading
the effectiveness of EMI shielding.
Soft Switching
er
ta
1.3.3
tio
Figure 1.5: Operation principle of electromagnetic shielding
Di
ss
The technique of soft switching was first presented [15] in 1990 and has rapidly developed in
recent years [20, 21]. The main goal of soft switching is to reduce the switching loss when
converters operate in high frequencies by switching on and off at zero current or zero voltage.
Consequently, the high rates of changes in voltage and current are alleviated, thus EMI can be
reduced. The operation principle and the effectiveness of soft switching are shown in Figures 1.6
and 1.7, respectively.
Meanwhile, soft switching has its own limitations in improving EMC: the effect to reduce EMI
focuses on the frequency band 150kHz – 30MHz, but it almost does not work on the frequency
band 10kHz – 150KHz; and more components are needed, such as resonant inductors, resonant
capacitors, auxiliary diodes, and even auxiliary switches, which increases the power loss on the
other side and makes the design of switched mode converters more complicated.
1.3.4
Random Modulation
Random modulation is a new method proposed in the last two decades [29] to reduce EMI.
Random modulation means that the switch frequency is varied according to a given random
signal, thus the total energy is spread over a wider frequency band, which can be illustrated as
in Figure 1.8.
The peaks appearing in the frequency band when converters operate in periodic mode can be
reduced and eliminated. In this way, EMI can be suppressed. For random modulation, there
are two main limitations: one is that in practice real random signals are difficult to generate,
and the other is that the design of converter parameters becomes difficult, since it is based on
7
Li
1 Introduction
(b) Turn-off process of hard switching
n
Ho
ng
(a) Turn-on process of hard switching
tio
(c) Turn-on process of soft switching
(d) Turn-off process of soft switching
Di
ss
er
ta
Figure 1.6: The turn-on and turn-off processes of a hard-switching and a soft-switching MOSFET
(a) Hard switching
(b) Soft switching
Figure 1.7: The power-loss waveforms for a power MOSFET used in a DC-DC converter with
hard- or soft-switching topologies
1 Introduction
ng
Li
8
Ho
Figure 1.8: Spectrum of a frequency-modulated sine signal following a sine modulation profile
in time (Initial frequency fC , peak deviation ∆fC )
1.4
Motivation
tio
n
the random frequency, for example, when a converter operates in frequency f1 , the equivalent
inductance is 2πf1 L. Due to the difficulty of obtaining a real random signal, a pseudo-random
signal is used, which is called pseudo-random modulation. Chaotic modulation is one kind of
common and important pseudo-random modulation, since chaos is characterized by pseudorandomness and continuous spectra, and can be generated by deterministic equations [27].
Di
ss
er
ta
Using chaos theory in engineering applications has emerged as an attractive new concept.
Chaos as a special dynamical phenomenon has extensively been studied for more than four
decades, but only recently it has been put forward for scientific and engineering applications.
The continuous-spectrum feature of chaos is perfectly fitting to fight EMI by spreading the
spectra of output signals over the entire frequency band and, thus, the peaks, which appear at
the multiples of the fundamental frequency and lead to EMI, can be suppressed, implying the
reduction of EMI.
Having this feature in mind, we focus on DC-DC converter circuits themselves by integrating
chaotic carriers with some conventional control methods for DC-DC converters, such as PWM
control, to propose some novel chaos-based control methods, which cannot only overcome the
disadvantages of conventional EMI filters and electromagnetic shielding, but also solve some
problems like big ripples of output current resulting from using chaos control. Therefore, the
proposed methods will be a perfect solution for EMI suppression. Simulations and experiments
will be carried out to verify the effectiveness of the methods, which lays a foundation for future
marketing.
In addition, some theoretical problems, such as stability, parameter design, and ripple estimation for DC-DC converters with chaos controls will be addressed to facilitate system design.
1.5
About this Dissertation
This thesis aims to propose approaches to fight EMI in the widely applied DC-DC converters
by employing chaos control, to carry out simulations and hardware implementations, and to
1 Introduction
9
Di
ss
er
ta
tio
n
Ho
ng
Li
provide theoretical analyses on some important issues, like stability and ripple estimation. It
is organised in the following way.
Chapter 2 is to give an overview to the chaos control of DC-DC converters, which is classified
into two categories, parameter modulation and chaotic PWM control.
Chapter 3 focuses on improving chaos control via parameter modulation in terms of ripples.
Although this kind of chaos control applied to DC-DC converters has the advantage of EMI
reduction, there is a big problem that the output ripples of DC-DC converters are too big to
be useful in practice. To cope with it, a novel chaos control method for ripple suppression is
proposed and analysed. The chaotic mapping of a peak current boost converter with this novel
chaos control is derived, which can facilitate further theoretical analysis.
Chapter 4 introduces the concept of chaos into traditional PWM control. Unlike chaos control
via parameter modulation, chaotic PWM control drives DC-DC converters to operate in chaotic
mode by adding external chaotic signals, which renders the design of DC-DC converters more
flexible. Since the external chaotic signals, i.e., chaotic carriers, can be generated by digital
processors, accordingly the magnitudes of ripples can also be controlled by computer programs.
Simulation and experimental results illustrate the effectiveness of this novel chaos control for
EMI reduction. Moreover, to realise chaotic PWM control, control circuits more complicated
than those for traditional PWM control need be implemented. Fortunately, these control
circuits can be integrated on printed circuit boards or even in small chips.
Chapter 5 deals with further improvements of chaotic PWM control. Considering the relatively high costs and speed limitations of digital processors, the chaotic carrier generated by
a digital processor will be re-designed and replaced by a novel analogue chaotic carrier suiting high-frequency DC-DC converters. The design of the analogue chaotic carrier is detailed,
and eventually, the evident EMI reduction can be observed at and proved by a DC-DC converter using the analogue chaotic carrier with the help of both simulation and experiments in
comparison with the EMI of a DC-DC converter controlled by traditional PWM.
Chapter 6 notices the different principles of reducing EMI by the popular soft switching technique and chaos control. It is well known that soft switching can reduce EMI for DC-DC
converters, by turning the switchs on or off at zero current or zero voltage to alleviate the high
rates of changes of voltage and current, thus reducing both switching loss and EMI; while chaos
control reduces EMI by spreading the spectra of signals or time series over the whole frequency
band. Obviously, soft switching and chaos control provide different ways to suppress EMI. In
Chapter 6, these two methods are combined, named chaotic soft switching PWM control, for
more pronounced improvement of EMC for DC-DC converters.
Chapters 7 and 8 address some theoretical considerations on chaotically controlled DC-DC
converters. Firstly, the chaotic features of DC-DC converters using chaos control via parameter
modulation are deduced and analysed, and some applications based on these analytical results
are given in Chapter 7. The analysis is carried out further for DC-DC converters using chaotic
PWM control in Chapter 8, where stability and estimations of ripples and outputs for this kind
of chaotic DC-DC converters are investigated, too.
Chapter 9 attempts to find an appropriate spectral estimation method for chaotic signals. It is
known that EMI is conventionally estimated by measuring its spectrum which is then subjected
to fast Fourier transform (FFT). However, due to the special characteristics of chaotic signals,
such as inner harmonics, FFT has evident drawbacks in analysing chaotic spectra. Here, a new
spectral estimation method, the Prony method, is employed to analyse chaotic spectra in order
to improve spectral resolution.
Chapter 10 summarises this dissertation, outlines the contributions made, and points out directions for further research.
10
2 Chaos Control of EMI
Chapter 2
Li
Chaos Control of EMI
Ho
ng
Chaotic phenomena exist ubiquitously in nature. As non-linear systems, DC-DC converters can
exhibit chaotic behaviour. The chaotic behaviour of DC-DC converters as well as chaos control
approaches to suppress EMI in DC-DC converters are introduced in this chapter. Further,
analytical tools for chaos, such as bifurcation diagram, Poincaré section and spectrum, are
illustrated. The advantages and disadvantages of these chaos control approaches are described,
showing the research direction to follow in this dissertation.
Chaos in DC-DC Converters
n
2.1
Di
ss
er
ta
tio
Since E. Lorenz discovered in 1963 the first physical chaotic system, viz., the Lorenz attractor,
chaos has matured as a science, and is considered as one of the three seminal scientific discoveries
of the twentieth century, together with relativity and quantum mechanics. Chaos typically refers
to unpredictability. Mathematically, chaos means a deterministic aperiodic behaviour, which
is very sensitive to its initial conditions, known as “butterfly effect”, saying that a butterfly
flapping its wings in Kansas can cause a tornado in Oklahoma a few days later [13]. Chaos
theory describes the behaviour of certain non-linear dynamical systems that under certain
conditions exhibiting chaos.
Since chaotic phenomena in DC-DC converters were first reported in [26], great efforts have
been devoted to study chaotic phenomena in various converters, such as boost, buck, boostbuck, and Cuk converters [1, 27, 59]. DC-DC converters are strongly non-linear systems and
can, thus, exhibit rich chaotic behaviour. As an example, periodic and chaotic behaviour can
be observed in a current mode boost converter under certain parameter conditions.
2.1.1
System Description
Typical DC-DC converters include buck, boost, buck-boost converters, and some other variations. Due to its simple model, the boost converter is taken here as an example and described
as follows [25],
xn+1 = f (xn ) = α(1 − xn ) mod 1,
(2.1)
V̄0
(Iref − in )L
tn
,α=
− 1, tn =
, tn is the switching-on time length at the nth
TC
VI
VI
switch, in the inductor current at the instant of switching on, TC the clock period, Iref the
reference current, VI the given input voltage, and V̄O the average output voltage. The circuit
diagram of the peak current mode controlled boost converter is depicted in Figure 2.1 (a) and
the current waveform i is shown in Figure 2.1 (b). It is obvious that α > 0 if V̄O > VI . Based on
where xn =
2 Chaos Control of EMI
11
Li
the criterion for the Lyapunov exponent, when α > 1, the sequence {x0 , x1 , x2 , . . .} is chaotic
within [0, α] [44].
(a)
(b)
Experimental Observations
Ho
2.1.2
ng
Figure 2.1: (a) Peak current mode controlled boost converter, (b) current waveform i(t)
Di
ss
er
ta
tio
n
The circuit parameters are set as follows: VI = 10V , L = 1mH, C = 92µF , Tc = 100µs,
A = 8.4, and Iref = 1.8A. Here, A is the amplifier’s gain, and the load resistance RL serves as
the control parameter.
The MOSFET IRF530 is selected here as the power switch, whose drain-to-source breakdown
voltage and continuous drain current are 100V and 14A, respectively. Since the maximum
reverse voltage of the fly-wheel diode is about 16V when the MOSFET is on, and the maximum
current is about 4A, the diode MBR20100CT is selected, whose withstand voltage is 63V and
rating current is 10A.
Setting the value of RL to 8Ω, 12Ω, 14Ω, 15Ω, or 16.5Ω, the boost converter can operate in four
periodic or chaotic modes, respectively, as shown in Figure 2.2 (the x-axis represents time, the
y-axis inductor current (upper) and output voltage (lower)) and Figure 2.3 (inductor current
given on the x-axis and output voltage on the y-axis).
It is seen that the boost converter exhibits periodic or chaotic behaviour under certain parameter
conditions, the ripples of the current and voltage become very big in chaotic mode, and the
average values of current and voltage vary as parameters are changed, which is not allowed for
DC-DC converters in most cases in practice.
2.1.3
Chaos Control
Today, it is well known that most conventional control methods and many special techniques
can be used for chaos control, regardless whether the purpose is to reduce “bad” chaos or
to introduce “good” chaos. Numerous control methodologies have been proposed, developed,
tested, and applied. Similar to conventional systems control, the concept of “controlling chaos”
is first to mean ordering or suppressing chaos in the sense of stabilising chaotic system responses.
In this pursuit, numerical and experimental simulations have convincingly demonstrated that
chaotic systems respond well to these control strategies. These methods of ordering chaos
include the now familiar OGY method [58], feedback controls, and fuzzy control, to list just a
few.
However, controlling chaos has also encompassed many non-traditional tasks, particularly those
of enhancing or generating chaos when it is beneficial. The process of chaos control is now
understood as a transition between chaos and order, and sometimes from order to chaos, depending on the application of interest. The task of purposely creating chaos, sometimes called
12
2 Chaos Control of EMI
(b) Period-2
Ho
ng
Li
(a) Period-1
(d) Period-4
er
ta
tio
n
(c) Period-3
Di
ss
(e) Chaos
Figure 2.2: Waveforms of inductor current (A) (upper) and capacitor voltage
(V) (lower) for different modes
chaotification or anticontrol of chaos, has attracted increasing attention in recent years due
to its great potential in non-traditional applications such as those found within the context
of physical, chemical, mechanical, electrical, optical, and particularly biological and medical
systems.
It was shown in the last subsection that a DC-DC converter running in chaotic mode has large
current and voltage ripples, and that it is difficult to design circuitry parameters. This is not
acceptable in practice. Therefore, it seems that chaos should be avoided in DC-DC converters.
On the other hand, chaos has the prominent feature of a continuous power spectrum, which
can be used to spread the spectra of the output signals over the whole frequency band, and
thus allows the peaks can be suppressed, which appear at the multiples of the fundamental
frequency and lead to EMI, implying the reduction of EM [27]. Here, a question is if there
is an approach, which can utilise the beneficial feature of chaos, but overcome the drawbacks
resulting from the use of chaos control? As we shall show, the answer is positive.
2 Chaos Control of EMI
13
(b) Period-2
Ho
ng
Li
(a) Period-1
(d) Period-4
er
ta
tio
n
(c) Period-3
Approaches of Chaos Control for EMI Suppression
Di
2.2
ss
(e) Chaos
Figure 2.3: Phase portraits (V − A) for
different modes
Fundamentally, chaos control methodologies can be divided into two categories: one is to
modulate circuitry parameters without any auxiliary circuits, while the other one is to append
external chaotic circuits to the main control parts to drive entire systems chaotic. The second
methodology is mainly involved with the widely used PWM control, thus it is called chaotic
PWM control.
2.2.1
Chaos Control via Parameter Modulation
To illustrate the chaos control method by parameter modulation, the voltage-controlled buck
converter shown in Figure 2.4 is used here.
The output voltage v of the converter is the non-inverting input to the amplifier, and the
reference voltage Vref is the inverting input to the amplifier. The gain of the amplifier is A.
The controlled output voltage vco can be expressed as
vco = A(vo − Vref ).
(2.2)
14
2 Chaos Control of EMI
vramp
VU
VL t
vco
i
S
E
A
L
D
C
v
R
ng
Figure 2.4: Voltage-controlled buck converter
Li
C1
Ho
This controlled voltage vco is the inverting input of the comparator and the non-inverting one
is the saw-tooth carrier vramp , which has the period T , the lower limit VL and the upper limit
VU , and satisfies the relationship,
vramp = VL + (VU − VL )[t mod T ],
(2.3)
er
ta
tio
n
where mod refers to the modulo operation.
The switch S is controlled by the pulse signal from the output of the comparator C1 . Assume
that the converter operates in continuous current mode (CCM). As vco < vramp , the output
of the comparator is at high level, S is on and diode D is off, which corresponds to Mode I;
and as vco > vramp , the output of the comparator is at low level, S is off and D is conducting,
which corresponds to Mode II. According to circuitry theory, the state equations of the buck
converter can be written as
Di
ss
ẋ = A1 x + B1 E for Mode I,
(2.4)
ẋ = A2 x + B2 E for Mode II,
(2.5)
1
T
− RC C1
0
0
, B1 = 1 , and B2 =
are state matrices.
where, x = v i , and A1 = A2 =
1
−L 0
0
L
Chaos control by parameter modulation means that the system can exhibit chaos by only tuning
one or more system parameters. Now some examples will be shown. First, the parameters of
the buck converter which operates in periodic mode are: L = 20mH, C = 47µF , A = 8.4,
VL = 3.8V , VU = 8.2V , TC = 400µs, R = 22Ω, Vref = 11.3V , and E = 20V .
To illustrate this method, the input voltage E is used as the control parameter, and the bifurcation diagram of E vs. i is depicted in Figure 2.5. From the figure it is seen that, when E is
larger than about 32.3, the buck converter begins to operate chaotically. It is remarked that
the values of the control variable, such as E here, with which the DC-DC converter exhibits
chaotic behaviour, can be derived by solving the Lyapunov exponents of the Jacobian matrix
of the state equations [9].
The Poincaré section provides another means to visualise an otherwise messy, possibly aperiodic, attractor. A Poincaré map is the intersection of a periodic orbit in the state space of a
continuous dynamical system with a certain lower-dimensional subspace, called the Poincaré
section, transversal to the flow of the system, as shown in Figure 2.6. It can be interpreted as a
discrete dynamical system within a state space that is one dimension smaller than the original
continuous dynamical system. Since it preserves many properties of periodic and quasi-periodic
15
ng
Li
2 Chaos Control of EMI
Ho
Figure 2.5: Bifurcation diagram (E ∼ i)
Di
ss
er
ta
tio
n
orbits of the original system and has a lower-dimensional state space, it is often used to analyse
the original system.
Figure 2.6: Illustration of Poincaré section
In terms of power spectra, there are three types of flows, viz., periodic, quasi-periodic, and
aperiodic. A fixed point, a closed curve, and a point cloud on the Poincaré section correspond
to a closed orbit, a quasi-periodic flow, and an aperiodic flow or chaos in the original state
space, respectively.
Similarly, to illustrate the chaotic behaviour in the voltage-controlled buck converter, the
Poincaré section can be selected in the way shown in Figure 2.7, where the planes S = 1
and S = 0 are called “switching planes”. Passing through the planes, the switch will change its
state from turned-on to turned-off (S = 0), or from turned-off to turned-on (S = 1) [28, 52].
Here, plane S = 1 is selected as the Poincaré section of the buck converter, and the corresponding Poincaré map is shown in Figure 2.8, where vn and in mean the values of output voltage
and input current at the instant of the switch being on, respectively. It is seen that the DC-DC
buck converter operates in chaotic mode when E = 37V .
It is remarked that some other parameters, such as Vref , can also be used as control parameter,
for instance, as shown by the bifurcation diagram of Vref vs. i with E = 30V in Figure 2.9(a).
Similarly, the Poincaré section of the buck converter at Vref = 25V and E = 30V is shown in
16
2 Chaos Control of EMI
S=1
Poincare Section
(in, vn)
Mode I
n
Ho
S=0
ng
Li
Mode II
tio
Figure 2.7: Selection of Poincaré section for a DC-DC converter
Di
ss
er
ta
Figure 2.9(b).
Moreover, the bifurcation diagram of 1/R vs. i with Vref = 11.3V and E = 35V is shown
in Figure 2.10(a), and the corresponding Poincaré cross section of the buck converter, when
R = 12.2Ω, is shown in Figure 2.10(b), respectively.
It is remarked that DC-DC converters can exhibit rich chaotic behaviour by tuning circuitry
parameters. For comparison, the spectra of the buck converter operating in periodic mode
and in chaotic mode are given in Figures 2.11 and 2.12, respectively. It is seen that the peak
Figure 2.8: Poincaré section
17
Ho
ng
Li
2 Chaos Control of EMI
(a) Bifurcation of Vref vs. i
(b) Poincaré section
Di
ss
er
ta
tio
n
Figure 2.9: Bifurcation and Poincaré section
(a) Bifurcation of 1/R vs. i
(b) Poincaré section
Figure 2.10: Bifurcation and Poincaré section
18
2 Chaos Control of EMI
values of the spectrum are greatly reduced when the buck converter operates in chaotic mode,
as compared with those when it runs in periodic mode.
40
20
Amplitude
0
-20
-40
-60
0
10
Frame: 63
20
30
40
50
60
Frequency (kHz)
70
80
90
100
ng
-100
Li
-80
Figure 2.11: Spectrum of the buck converter when E=31V
Ho
40
20
n
-20
-40
-60
-80
0
10
Frame: 105
20
30
40
50
60
Frequency (kHz)
er
ta
-100
tio
Amplitude
0
70
80
90
100
Remarks
ss
Figure 2.12: Spectrum of the buck converter when E=34V
Di
It is seen that DC-DC converters can exhibit rich chaotic behaviour by parameter modulation,
which is used to reduce EMI as shown in Figures 2.11 and 2.12. Meanwhile, it is also observed
that the output ripples of the DC-DC converter with chaotic parameter modulation control are
obviously increased. As shown in Figure 2.1, the ripple of the boost converter’s input current
is 0.38A with periodic control, while it increases to more than 0.7A under chaotic parameter
modulation control. Since the main function of DC-DC converters is to provide stable and
smooth power supply, large ripple is not allowed for DC-DC converters in practice.
On the other hand, the chaotic parameter modulation control approach makes system design
difficult, because the operation frequency of a chaotic system is uncertain. Furthermore, DCDC converters with chaotic parameter modulation control may run out of chaotic regions when
their power supplies or loads fluctuate. These fluctuations are normally unpredictable, because
the input voltages (or loads) of DC-DC converters, such as E, are supplied by other DC sources
or batteries, and changes of these DC voltages can influence the operation modes (chaotic or
periodic mode) of DC-DC converters according to the bifurcation diagram. Finally, there is a
lack of theory, such as to estimate the mean switching frequency of chaotic DC-DC converters,
so that system design becomes difficult.
19
Li
2 Chaos Control of EMI
(a) periodic waveforms
(b) chaotic waveforms
2.2.2
ng
Figure 2.13: Periodic and chaotic input current waveforms of a buck converter
Chaotic PWM Control
Summary
tio
2.3
n
Ho
Due to the above mentioned disadvantages of chaotic parameter modulation, merging chaos
control with the most popular and successful control method for DC-DC converters, viz., PWM,
in order to reduce EMI constitutes the main concern of this dissertation, which is to be detailed
in Chapters 4 – 6.
Di
ss
er
ta
In this chapter, it has been shown that DC-DC converters can exhibit chaotic behaviour under
certain parameter conditions. Therefore, the use of chaos control is possible. This chapter
introduced chaotic parameter modulation and its drawbacks, and pointed out a potential chaotic
PWM control for EMI suppression to be detailed in this dissertation.
20
3 Chaotic Peak Current Mode Boost Converters
Chapter 3
ng
Li
Chaotic Peak Current Mode Boost
Converters
Introduction
tio
3.1
n
Ho
A by-product of applying chaos control in reducing EMI are the increased output ripples of
DC-DC converters, which are not acceptable in practice. In this chapter, a novel chaotic peak
current mode boost converter is proposed, which is based on parameter modulation and can
effectively restrain the ripples. A current mapping function is derived, and its chaotic behaviour
is analysed. Further, simulations and experiments are carried out to illustrate the effectiveness
of the proposed design in reducing EMI and restraining the output ripples of the converter.
Di
ss
er
ta
Over the last two decades, chaotic parameter modulation control to the end of reducing EMI
in DC-DC converters has attracted great interest [3, 4, 6, 25, 27, 32, 33, 57, 75, 76]. Since the
pioneering work of Deane and Hamill [27], who used chaotic parameter modulation control to
design a peak current mode controlled boost converter, some variations have been proposed
and tested [32, 33], showing that in power converters EMC can effectively be improved by the
introduction of chaos via current mode control.
A detailed study on a chaotic DC-DC converter has also been carried out by computing its
periodic spectral components [25]. For the same purpose of improving EMC, the switching
operation of a boost converter controlled by a chaotic return map was proposed in [6], and
the spectral analysis of the converter’s input current demonstrates how a return map affects
the power density spectrum of the input current, which provides an approach to design the
return map to satisfy EMC standards. Further experimental research of a chaos-based currentprogrammed boost converter was reported in [3].
Despite of the success of applying chaos control in EMI suppression, there remain two prominent
problems unsolved, viz., the ripples of the outputs are much greater than those of periodically
running DC-DC converters [4], and the power of the background spectra has been increased in
most designs of chaos control by parameter modulation, resulting in larger power consumption,
although the peak values of the power spectrum are reduced. Since the basic purpose of DC-DC
converters is supplying power, large ripples simply imply a degradation of performance. This
problem has previously been pointed out, and an explicit expression between the ripples and
the spectral spread of the current was given in [5]. Anyway, it is a difficult task to design a
suitable control suppressing the ripples to a desired level.
These two disadvantages do not only exist in the peak current mode controlled boost converters, but also in other chaotic power converters [57, 75], which have seriously impeded their
popularity.
3 Chaotic Peak Current Mode Boost Converters
21
3.2
Ho
ng
Li
Hence, answering the questions of how to improve the control method for chaotic DC-DC
converters so that both low EMI and small output ripples can be achieved simultaneously, and
how to verify the relationship between the ripples and the background spectrum constitute the
concern of this chapter.
This chapter proposes a novel chaotic peak current mode control by setting a lower limit for
the controlled current, by which the ripple can easily be restrained between the peak value,
i.e., the upper limit, and the lower limit. Meanwhile, the chaotic characteristics of the DC-DC
converter are well maintained.
Compared with other peak current mode controls, where there is only one control input, the
peak current (upper limit), the proposed chaotic peak current mode control leads to more
complex and richer chaotic behaviour in the DC-DC converters.
This chapter is organised as follows. In Section 3.2, a novel peak current mode boost converter
is presented and its corresponding chaotic mapping function is derived. The characteristics
of the mapping are then analysed in Section 3.3 with focus on its spectrum, and bifurcating
and chaotic behaviour. Its effects on EMI reduction and ripple suppression are studied and
illustrated with simulations. To further verify this approach, the entire system is built and
experimental results are presented in Section 3.4.
Chaotic Current Mode Boost Converter Model
Di
ss
er
ta
tio
n
Inspired by [25], a novel chaotic current mode boost converter is proposed and depicted in
Figure 3.1.
Figure 3.1: A chaotic current mode boost converter
Unlike the design in [25], the switch S is now controlled by a clock with period TC , a lower
reference current signal and an upper one, denoted by Ilow and Iupp , respectively. Different
inductor current waveforms can be obtained as shown in Figures 3.2 (a)–(c), corresponding to
the following three cases, respectively:
1. Case I: t2 ≥ TC ,
2. Case II: TA ≥ TC > t2 , and
3 Chaotic Peak Current Mode Boost Converters
Li
22
tio
n
Ho
ng
(a) Case I: t2 ≥ TC
Di
ss
er
ta
(b) Case II: TA ≥ TC > t2
(c) Case III: TC ≥ TA
Figure 3.2: Different current waveforms i(t) obtained from the boost converter
3. Case III: TC ≥ TA ,
where t1 is the time for i(t) to rise from Ilow to Iupp , t2 is the time for i(t) to fall from Iupp to
Ilow , and TA = t1 + t2 .
In order to facilitate the analysis of the proposed converter, the discrete-time mapping of i(t)
is derived.
Referring to Figure 3.2, the time interval of variant length [in , in+1 ) is focused, in which i(t)
changes from in to in+1 , with in defined as the inductor current sampled at the instants of the
clock pulses as i(t) is decreasing (e.g., in in Figures 3.2 (a)–(c)) and the instants of the clock
pulses as i(t) is increasing with switch S activated twice or more within a single clock cycle
(e.g. in+2 in Figures 3.2 (b) and (c)). For clarity, a time mapping is also assumed, such that
3 Chaotic Peak Current Mode Boost Converters
23
i(τn ) = in when τn = 0.
Referring to Figure 3.2, S is closed at τn = 0, and hence
di
= VLI ,
dτn
i(τn ) = in + VLI τn ,
(3.1)
where VI is input voltage and L the inductance.
Let tn be the time required for the current to rise from in to Iupp . Based on (3.1), one has
(Iupp − in )L
.
VI
The switch S is then opened and i(τn ) is governed by
where V O is the mean output voltage. Therefore,
VI − V O
(τn − tn )
L
Ho
i(τn ) = Iupp +
(3.3)
ng
di
(VI − V O )
=
,
dτn
L
(3.2)
Li
tn =
(3.4)
3
tio
n
until the next clock pulse arrives or i(τn ) = Ilow .
As explained in [25], it is possible to estimate the mean output voltage V O by equating the
mean of the aperiodic inductor current to a periodic one. It is derived that V O is governed by
the input-output relationship,
V O + V O (VI Tp /2L − Iupp )RVI − RTp VI3 /2L = 0,
(3.5)
Di
ss
er
ta
where Tp = TC is based on the design given in [25].
Here, a similar approximation is performed, and (3.5) is still applicable, except that Tp does not
only depend on TC , but also on the values of Iupp and Ilow for the Cases II and III — which are
our main concern. It is also observed that Tp is proportional to Iupp but inversely proportional
to Ilow . Using the first-order approximation, Tp can be expressed as
Iupp
+ b TC ,
(3.6)
Tp = a
Ilow
where a and b are constants to be determined. Based on extensive experimental results, it is
found that a = 2.0499 and b = 1.5455 and, hence, V O can be obtained by solving (3.5). Based
on circuit simulation, the relative errors of V O are well within 2%, which is much better than
the ones obtained by [25].
0
Now, let tn be the time interval from the last action of S within a clock period to the next
clock pulse, which can be given as
(
ε
if ε ≤ t2 ,
0
tn =
(3.7)
ε − t2 otherwise,
where ε = [TC − (tn mod TC )] mod TA .
Referring to Figure 3.2, we obtain
(
O)
Iupp + (VI −V
ε if ε ≤ t2 ,
L
in+1 =
VI
Ilow + L (ε − t2 ) otherwise.
(3.8)
24
3 Chaotic Peak Current Mode Boost Converters
Defining
xn =
tn
(Iupp − in )L
=
TC
VI TC
and
α=
VO
− 1,
VI
based on (3.8), a chaotic mapping can be constructed as
if x0n ≤ γ,
αx0n ,
xn+1 =
ρ + γ − x0n , otherwise,
(3.9)
ng
1
x0n = β{[ (1 − (xn mod 1))] mod 1},
β
t2
TA
(Iupp − Ilow )L
γ =
, β=
and ρ =
.
TC
TC
VI TC
Li
where
It should be noticed that, for Case I or t2 > TC , (3.9) can be simplified as
mod 1)] ,
Ho
xn+1 = α [1 − (xn
which is equivalent to the chaotic mapping obtained in [25]. Therefore, the situation in [25]
can be considered as a special case of the one studied in this chapter.
Characteristics of the Chaotic Mapping
tio
n
3.3
3.3.1
er
ta
In this section, the characteristics of the chaotic mapping (3.9) are studied. Although these
characteristics depend on the all related parameters, such as VI and R, the study here will only
focus on their dependence on Ilow . Hence, referring to Figure 3.1, the following parameters are
assumed fixed as VI = 10V , L = 1mH, C = 12µF , TC = 100µs, and R = 30Ω.
Spectrum Analysis
Di
ss
As explained in Section 3.2, there are three possible cases associated with the reference currents.
Throughout this chapter, it is assumed that Iupp = 4A while Ilow takes values of 0A, 3A and
3.5A, for Cases I, II, and III, respectively.
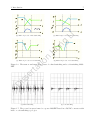
Figure 3.3 shows the time evolutions of the inductor currents i(t) and the corresponding spectra
for the three cases. Comparing the waveforms in Figures 3.3 (a), (c) and (e), it can be observed
that the ripples of i(t) are greatly reduced when a larger Ilow is applied. Moreover, it is shown
by the spectra in Figures 3.3 (b), (d), and (f) that power is well spread over the entire frequency
band. It is also interesting to notice that, instead of having a maximum peak of a magnitude
close to the clock frequency TC as in Cases I and II, in Case III the peak is shifted to a frequency
close to T1A = 13.9kHz.
Since the low-frequency components are suppressed, a better spectrum distribution is obtained
in all cases. However, it is also noticed that the background spectrum is not significantly
improved with the reduction of current ripples.
3.3.2
Bifurcation and Lyapunov Exponents
The broadband spectrum discussed in the previous section suggests the chaotic nature of the
boost converter expressed in (3.9). In the sequel, this nature is further investigated with the
use of bifurcation diagram and Lyapunov exponents.
3 Chaotic Peak Current Mode Boost Converters
(b) Spectrum of (a)
Ho
ng
Li
(a) i(t) for Case I
25
(d) Spectrum of (c)
er
ta
tio
n
(c) i(t) for Case II
(f) Spectrum of (e)
ss
(e) i(t) for Case III
Di
Figure 3.3: (a, b) Case I: t2 ≥ TC ; (c, d) Case II: TA ≥ TC > t2 ; (e, f) Case III: TC ≥ TA
Figure 3.4 depicts the bifurcation diagram of xn vs. Ilow and the corresponding maximum
Lyapunov exponent spectrum (LEs). The chaotic nature is confirmed with the existence of a
positive LEs, while some periodic windows are observed in between. According to (3.9), periodic
windows exist when ρ + γ = β, and (3.9) can be written as xn+1 = β(1 − β1 x0n ) corresponding
to LE = 0.
Similarly, the bifurcation diagrams of xn vs. VI and xn vs. TC are obtained and shown in
Figures 3.5 and 3.6. In Figure 3.5, a route from periodicity to chaos is clearly observed when
the input voltage VI is decreased although some periodic windows exist. A similar conclusion
can be drawn from the bifurcation diagram given in Figure 3.6. Therefore, the mapping (3.9)
can generate rich dynamical behaviour like bifurcation and chaos, which constitutes the corner
stone of the proposed approach to reduce EMI and improve EMC.
3 Chaotic Peak Current Mode Boost Converters
Li
26
(a) Bifurcation of xn vs. Ilow
(b) Maximum LE
er
ta
tio
n
Ho
ng
Figure 3.4: Bifurcation of xn vs. Ilow and corresponding maximum LE
(a) Bifurcation of xn vs. VI
(b) Maximum LE
Di
ss
Figure 3.5: Bifurcation of xn vs. VI and corresponding maximum LE
(a) Bifurcation of xn vs. TC
(b) Maximum LE
Figure 3.6: Bifurcation of xn vs. TC and corresponding maximum LE
3 Chaotic Peak Current Mode Boost Converters
3.3.3
27
EMC Performance
(b) Ilow = 2.62A
ss
er
ta
tio
n
(a) Ilow = 1.979A
Ho
ng
Li
In this subsection, the EMC performance of the proposed chaotic peak current mode boost
converter is studied. As shown in the bifurcation diagram, the boost converter can operate
either in chaotic or periodic mode. Therefore, simulations are to be conducted to compare
which mode provides better EMI suppression performance.
(d) Ilow = 0A
(e) Ilow = 2.4A
(f) Ilow = 3A
Di
(c) Ilow = 2.958A
Figure 3.7: Spectra for different Ilow : (a)–(c) periodic mode and (d)–(e) chaotic mode
28
3 Chaotic Peak Current Mode Boost Converters
3.4
Ho
ng
Li
It can be observed in Figure 3.4 (a) that the boost converter operates in periodic mode at, e.g.,
Ilow = 1.979A, 2.62A, and 2.958A (Iupp = 4A) among many other options, while the power
spectra of the corresponding inductor currents are depicted in Figure 3.7 (a)–(c). It reveals
that the peak amplitude remains almost the same with the fundamental frequency shifting to
a higher frequency as Ilow increases, which implies that the EMI is not increased, while the
increase of Ilow means a decrease of ripple amplitudes.
On the contrary, Figures 3.7 (d)–(f) depict the spectra when the boost converter operates in
chaotic mode with Ilow = 0A, 2.4A, and 3A (Iupp = 4A) for the three specific cases. A smaller
maximum peak value is obtained when Ilow = 3A, as compared with the case of Ilow = 0A,
corresponding to the original design given in [25], which means that the EMC of the boost
converter is improved, and a slight shift of the fundamental frequency is also observed.
It is remarked that, theoretically, Ilow can be infinitesimally close to Iupp to restrain the current
ripple to very small values. Due to the limited operation frequency of real switches, implemented
with MOSFETs, IGBTs etc., however, Ilow is dependent on the combination of the switches’
operation frequency, ripple requirement, and EMC standards.
Therefore, it can be concluded that, by controlling the boost converter to run in chaotic mode,
the switch control strategy proposed in Figure 3.1 cannot only suppress the ripples, but also
improve the EMC at the same time.
Experimental Verification
tio
n
The design shown in Figure 3.1 is realised with discrete components, the major ones of which
are tabulated in Table 3.1. Assume that VI = 10V , TC = 100µs, L = 0.56mH, C = 47µF , and
R = 30Ω.
Di
ss
er
ta
Table 3.1: List of main components
Component
Device
diode
MBR2045CT
switch
IRFZ234N
current sensor
LA-55-P
flip-flop
74HC74N
comparator
LM393
driver
34152P
Figure 3.8: Operation principle of LA 58-P mutual inductor
Current sampling is important in circuit implementation. In an experiment carried out for
verification purposes, a type LA 58-P mutual inductor is used to detect the input current. Its
operation principle is introduced in Figure 3.8, and its main characteristics are
3 Chaotic Peak Current Mode Boost Converters
29
+ : DC source +12V .. 15V
χ : Accuracy 0.5 %
- : DC source -12V .. 15V
f : Frequency band DC .. 200 kHz
RM : Measurement
KN : Conversion rate 1:1000
Di
ss
er
ta
tio
n
Ho
ng
Li
Since the conversion rate, i.e., IS :Ip , is equal to 1:1000, to obtain the real value of the measured
current, R should be 1000Ω in the experiment. Finally, the circuit is implemented as shown in
the circuit diagram Figure 3.9 as the circuit board shown in Figure 3.10.
Figure 3.9: Circuit diagram of the chaotic peak current mode boost converter
The current waveforms of the three cases with the boost converter operating in periodic mode
are depicted in Figures 3.11 (a), (c) and (e), while the corresponding spectra are given in
Figures 3.11 (b), (d) and (f). The experimental results are well matched by the simulations
presented in Section 3.3.3. It is also noticed that the maximum peaks of the spectra remain
unchanged, even though the ripples, which haves the sizes 2.4A, 1.4A, and 0.9, respectively,
have been reduced greatly.
Figure 3.12 shows the cases when the boost converter operates in chaotic mode. It is worth to
emphasize that the case presented in [25] is equivalent to that with Ilow = 0A. By comparing
the results depicted in Figure 3.12, an improvement of EMI suppression is clearly demonstrated
with an increase of Ilow , while a large reduction of the ripples can be achieved at the same time.
This is also consistent to the observations in Section 3.3.1 that there is no obvious relationship
between ripple magnitude and background spectrum.
3 Chaotic Peak Current Mode Boost Converters
tio
n
Ho
ng
Li
30
3.5
er
ta
Figure 3.10: Circuit board of the chaotic peak current mode boost converter
Summary
Di
ss
This chapter proposed a chaotic parameter modulation, i.e., a novel chaotic peak current mode
boost converter. This method cannot only reduce EMI but can also effectively restrain the
ripples. A current mapping function has been derived, with which its chaotic behaviour has
been analysed. Further, simulations and experiments have been carried out to illustrate the
effectiveness of the proposed design in reducing EMI and restraining the converter’s output
ripples.
31
ng
Li
3 Chaotic Peak Current Mode Boost Converters
(b) spectrum of (a)
er
ta
tio
n
Ho
(a) i(t) with Ilow = 1.6A
(d) spectrum of (c)
Di
ss
(c) i(t) with Ilow = 2.6A
(e) i(t) with Ilow = 3.1A
(f) spectrum of (e)
Figure 3.11: Current waveforms and corresponding spectra in periodic mode for three different
cases
3 Chaotic Peak Current Mode Boost Converters
ng
Li
32
(b) spectrum of (a)
er
ta
tio
n
Ho
(a) i(t) with Ilow = 0A
(d) spectrum of (c)
Di
ss
(c) i(t) with Ilow = 3A
(e) i(t) with Ilow = 3.2A
(f) spectrum of (e)
Figure 3.12: Current waveforms and corresponding spectra in chaotic mode for three different
cases
4 Chaotic Pulse Width Modulation
33
Chapter 4
Li
Chaotic Pulse Width Modulation
Introduction
tio
4.1
n
Ho
ng
Since pulse width modulation (PWM) control is the most common and important control
method for DC-DC converters, combining chaos control and PWM can distribute the harmonics
of DC-DC converters continuously and evenly over a wide frequency range, thereby reducing
the EMI. Simulation and experimental results are given to illustrate the effectiveness of the
proposed chaotic pulse width modulation (CPWM), which provides a good example of applying
chaos theory in engineering practice.
Di
ss
er
ta
It has been suggested in Chapter 3 and the literature [27, 34] that in a DC-DC converter chaos
control by parameter modulation can be used to reduce EMI. Although chaos is very desirable
in this case, there exist some by-products that need to be eliminated. The most prominent
one is the difficulty of design, because the circuit may run out of chaos when its power supply
or load fluctuate. As these fluctuations are normally unpredictable, this kind of chaos control
only suits DC-DC converters running under stable working condition. The second one are large
output ripples. Although in Chapter 3 some efforts have been devoted to this problem, the
control method proposed in Chapter 3 is only available for the controls with current reference
or voltage reference.
PWM control is the most popular and widely used control method for DC-DC converters,
and it can mainly be divided into three parts, sampling and error amplifying, PWM carrier,
and PWM signal output. Due to the cluster harmonics around the multiples of the carrier
frequency in output waveforms, for a DC-DC converter with PWM control is difficult to satisfy
the more and more strict international EMC standards. EMI filters are always needed as
auxiliary circuits together with DC-DC converters, which largely increase the products’ cost
and weight. Chaos provides a new way to reduce EMI for DC-DC converters. Therefore,
in this chapter, combining chaos with PWM, named chaotic PWM control, is proposed by
replacing the periodic PWM carrier by a chaotic one. The harmonics of DC-DC converters will
then be distributed continuously and evenly over a wide frequency range. Consequently, the
EMI can be controlled and reduced, and the EMC can be improved. Furthermore, the output
waveforms and spectral properties of the EMI will be analysed in Section 4.3 as the carrier
frequency changes with different chaotic maps, and an analysis of the chaotic PWM converter
as the carrier amplitudes change is conducted in Section 4.4. Both simulation and experimental
results are given to illustrate the effectiveness of the proposed CPWM. This provides a good
example of applying chaos theory in engineering practice.
34
4.2
4 Chaotic Pulse Width Modulation
Design Considerations
er
ta
tio
n
Ho
ng
Li
The output waveform of a DC-DC converter controlled by traditional PWM, as introduced in
[40], is constituted of many harmonic components. The distribution of harmonics is influenced
by the carrier. Carrier frequency f∆ and carrier amplitude A∆ are invariant under traditional
PWM, thus the spectrum has biggish peaks close to the carrier frequency and its multiples.
This makes it difficult for the DC-DC converter to satisfy the international EMC standards.
Conventionally, filters are used to reduce EMI of DC-DC converters. However, due to the
relationship between harmonics and signals, filters do not only restrain the harmonics but also
the effective current signals. Moreover, each filter can only restrain EMI in a certain, relatively
narrow frequency band. The existence of a number of biggish peaks of the spectrum under
traditional PWM makes it difficult to design filters for DC-DC converters. It is remarked that
the pulse width generated by traditional PWM is determined by the intersection of the carrier
and modulation waves. The carrier wave can have triangular or sawtooth shape.
ss
Figure 4.1: Chaotic PWM boost converter
Di
It is desirable for DC-DC converters to eliminate EMI without using filters. Since the distribution of harmonics is influenced by the carrier and the chaotic behaviour of DC-DC converters
can be used to reduce EMI, chaotic f∆ or chaotic A∆ are used to distribute the harmonics continuously and evenly over a wide frequency range. Although the total energy is not changed,
the peaks of the harmonics are reduced, thus EMI is restrained. Therefore, in order to obtain chaotic f∆ or chaotic A∆ , chaotic PWM (CPWM), as shown in Figure 4.1, is proposed,
analysed, and tested.
4.3
CPWM with Varying Carrier Frequencies
CPWM adopts triangular or sawtooth waves to modulate, but its carrier period T∆0 changes
according to
T∆0 =
xi
T∆
M ean(x)
(4.1)
4 Chaotic Pulse Width Modulation
35
(a) µ = 0.7
(b) µ = 0.8
(c) µ = 0.9
Li
Figure 4.2: Chaotic sequences generated by the tent map
N
X
i=1
N
xi
.
Ho
M ean(x) =
ng
where T∆ is the invariant period, xi , i = 1, 2, . . . , N , a chaotic sequence is denoted by x =
{x1 , x2 , . . . , N }, and M ean(x), the average of the sequence, is defined as
n
For simplicity, the tent map is employed here to generate chaotic sequences [35], which is
described as
2µxn
if xn 6 0.5,
f (xn ) =
(4.2)
2µ(1 − xn ) if xn > 0.5,
tio
with xn ∈ [0, 1]. Note that when 0.5 < µ < 1, |f 0 (xi )| > 1. Its Lyapunov exponent is
n
(4.3)
er
ta
1X
λ = lim
ln |f 0 (xi )| = ln (2µ) > 0.
n→∞ n
i=1
4.3.1
ss
The positive Lyapunov exponent implies that the system is chaotic. Figure 4.2 shows the
chaotic sequences of the map at µ = 0.7, µ = 0.8 and µ = 0.9, respectively. Therefore, chaotic
PWM is realised by properly tuning the period length of the carrier.
Simulations
Di
For practical evaluation of CPWM, here a boost converter is taken as test-bed and is described
as the main circuit in Figure 4.1. The values of its parameters are chosen as VI = 10V ,
L = 1mH, C = 330µF , RL = 15Ω, Iref = 2A, and T∆ = 0.0001s. Then, the modulation
waves, carrier and PWM waves of the boost converters controlled by traditional PWM and by
CPWM at µ = 0.7, 0.8, and 0.9 are simulated as shown in Figures 4.3 and 4.4, respectively.
The corresponding spectra are shown in Figure 4.5.
It is seen in Figure 4.5 that the peak values of the spectrum generated by traditional PWM
(Figure 4.5 (a)) may lead to exceed the limits set in EMC standards, while the spectrum
generated by CPWM distributes continuously and evenly over a wide frequency range (Figures 4.5 (b)–(d)), which satisfies the international EMC standards. Furthermore, by CPWM
the average switching frequency has been greatly reduced (Figure 4.4 (a)(c)(e)) as compared
with that by traditional PWM (Figure 4.3 (a)). This reduces the dissipation of DC-DC converters and enhances their stability. Meanwhile, it can be seen that increasing µ results in some
slightly larger ripples of the output waveforms and smoother spectra under CPWM. Therefore,
an appropriate µ needs to be determined to reach a good trade-off between ripples and spectra
in practice.
4 Chaotic Pulse Width Modulation
Li
36
(b) Current wave (upper), and
output voltage wave (lower)
ng
(a) PWM control signals
Ho
Figure 4.3: PWM control signals and output waveforms of the boost converter controlled by
traditional PWM
Spectral Characteristics
tio
n
Now, the logistic map and the shift map are employed to generate chaotic sequences, and then
their spectral characteristics are compared to that of the boost converter controlled by CPWM
with the tent map. The logistic map is defined as
f (xn ) = 1 − µx2n ,
(4.4)
er
ta
where x ∈ [−1, 1] and µ = 2.0, and the shift map as
if 0 6 xn 6 21 ,
if 12 < xn 6 1,
(4.5)
ss
f (xn ) =
µ xn − 21 + 1,
µ xn − 12 ,
Di
where x ∈ [0, 1] and µ = 1.8.
The output waveforms and spectra of the currents in the DC-DC converter controlled by CPWM
employing the logistic map and the shift map are shown in Figure 4.6. Comparing the spectra
in Figure 4.6 with that in Figure 4.5(d), it is seen that the current spectra with the logistic
and shift maps are better than that of the tent map. Comparing the output waveforms shows
that using the tent map leads to the least ripple. This means that various chaotic maps can be
used to design CPWM just dependent on the application of interest in practice.
4.3.2
Experiments
To verify the simulation results, an experiment is conducted. The block diagram of the experimental configuration is drawn in Figure 4.7.
The experimental results of using the logistic map are shown in Figures 4.8 – 4.10, which appear
to be consistent with the simulation results. Furthermore, in Figures 4.8 and 4.9 it is seen that
the peak values of the spectra in the low frequency band obtained by CPWM are reduced by
10% in comparison with those yielded by traditional PWM.
37
Li
4 Chaotic Pulse Width Modulation
(b) µ = 0.7
tio
n
Ho
ng
(a) µ = 0.7
(d) µ = 0.8
Di
ss
er
ta
(c) µ = 0.8
(e) µ = 0.9
(f) µ = 0.9
Figure 4.4: Control signals (left column) and current and output voltage waveforms (right
column) of the boost converter controlled by CPWM
4.4
CPWM with Varying Carrier Amplitudes
CPWM also adopts triangular or sawtooth waves to modulate, but its carrier amplitude A0∆
changes according to
A0∆ = {1 + λ
xi
}A∆ ,
M ean(x)
(4.6)
4 Chaotic Pulse Width Modulation
Li
38
(b) By CPWM at µ = 0.7
tio
n
Ho
ng
(a) By traditional PWM
(c) By CPWM at µ = 0.8
(d) By CPWM at µ = 0.9
er
ta
Figure 4.5: Spectra of the current in the boost converter controlled by traditional PWM and
CPWM, respectively
Simulations
Di
4.4.1
ss
where A∆ is the invariant amplitude, xi , i = 1, 2, . . ., a chaotic sequence, x = {x1 , x2 , . . .}, λ the
modulation factor of the amplitude, which is determined as required in practice, and M ean(x)
the average of the sequence as defined in Section 4.3.
The same converter with the same circuitry parameters as used in Section 4.3 is employed (see
Figure 4.1). Here, when A∆ = 1.5V , the same output voltage of the boost converter with
varying carrier frequency can be obtained. The logistic map is adopted to generate chaotic
sequences. Now, the output characteristics and spectra of the boost converter at λ = 0,
λ = 0.4, and λ = 0.8 are to be simulated.
At λ = 0, the output waveforms and PWM control signals are the same as the ones in Figure 4.3;
therefore, only the output waveforms and spectra at λ = 0.4 and λ = 0.8 are given here. The
output waveforms of the boost converter controlled by CPWM at λ = 0.4 and λ = 0.8 are
shown in Figure 4.11 (a) and (b). Figure 4.11 (c) and (d) show the inductor current spectra of
the boost converter at λ = 0.4 and λ = 0.8.
It is seen in Figure 4.11 that under CPWM control with varying amplitudes the ripples of
the output waveforms are relatively larger than under CPWM control with varying carrier
frequencies. However, their spectra are similar. It is also seen that as λ increases, the ripples of
the output waveforms increase, but the spectra remain unchanged. Thus, if the spectra already
satisfy the EMC standards, λ should be as small as possible in practice.
4 Chaotic Pulse Width Modulation
39
(b) Output waveform
with shift map
n
Ho
ng
Li
(a) Output waveform
with logistic map
tio
(c) Spectrum of current
with logistic map
(d) Spectrum of current
with shift map
Di
ss
er
ta
Figure 4.6: Output waveforms and spectra of currents in the boost converter controlled by
CPWM
Figure 4.7: Block diagram of experimental set-up
40
4 Chaotic Pulse Width Modulation
(a)
(b)
tio
(a)
n
Ho
ng
Li
Figure 4.8: Output waveforms and spectra of input current (a) and output voltage (b) of the
boost converter controlled by traditional PWM
(b)
Di
ss
er
ta
Figure 4.9: Output waveforms and spectra of input current (a) and output voltage (b) of the
boost converter controlled by CPWM
(a) Periodic carrier wave
(b) Chaotic carrier wave
(c) Periodic drive wave
(d) Chaotic drive wave
Figure 4.10: Comparison of two kinds of carrier waves and drive waves
4 Chaotic Pulse Width Modulation
41
(b) Outt waveform at λ = 0.8
n
Ho
ng
Li
(a) Output waveform at λ = 0.4
tio
(c) Current spectrum at λ = 0.4
(d) Current spectrum at λ = 0.8
4.4.2
er
ta
Figure 4.11: Output waveforms and current spectra of the boost converter controlled by CPWM
at λ = 0.4 and λ = 0.8
Experiments
Summary
Di
4.5
ss
Likewise, experimental results obtained by using the logistic map at λ = 0.4 are given to testify
the simulation results. It is shown in Figure 4.12 that they are consistent.
Chaotic PWM control has been proposed in this chapter. According to the results of simulations and experiments, it can be observed that the output spectra of DC-DC converters with
CPWM control can be distributed evenly over a wide frequency band, thus reducing EMI.
Some important problems, such as long-time stability or average value estimations of input
and output variables of DC-DC converters controlled by CPWM, remain to be answered in
Chapter 8.
4 Chaotic Pulse Width Modulation
(b) Chaotic carrier
Di
ss
er
ta
tio
(a) Periodic carrier
n
Ho
ng
Li
42
(c) Chaotic drive waveform
(d) Output waveform and its spectrum
Figure 4.12: Experimental waveforms of the boost converter with varying carrier amplitudes
5 Analogue Chaotic PWM
43
Chapter 5
Li
Analogue Chaotic PWM
5.1
Ho
ng
CPWM control can widely be applied in DC-DC converters and is very effective to suppress
EMI. However, the high cost of digitally generated chaotic carriers used in Chapter 4 greatly
impedes the applicability of this control. Thus, a novel method to generate a chaotic carrier in
analogue form using chaotic oscillators is to be proposed, analysed, simulated, and experimentally validated in this chapter.
Introduction
Di
ss
er
ta
tio
n
Generally, chaotic carriers can be generated in digital or analogue ways. The advantages of digitally generated chaotic carriers are that digital chaotic signals are accurate, and that frequency
and amplitude of the carriers can easily be adjusted by programming the digital processors
without changing their external interface circuits; while the disadvantages are also obvious,
namely, that the regulable frequency range of chaotic carriers generated by digital processors
is dependent on the speed of Digital Signal Processors (DSP) or other digital computers such
as single-chip ones, that sometimes external interface circuits are necessary, and that the costs
of digital chaotic carriers are high. On the other hand, the costs of analogue chaotic carrier are
much lower; and the regulable frequency range can be much broader by changing resistance and
capacitance of the analogue chaotic carrier circuits suitable to function in high-frequency DCDC converters. Furthermore, numerous existing chaotic oscillators can be employed to design
analogue chaotic carriers. However, analogue chaotic carriers cannot be adjusted as accurately
as digital ones due to the non-ideal performance characteristics of the components, and their
hardware implementation is a little more complex, since chaotic carriers are not realised by
programming, but by components.
It is known that DC-DC converters always operate with high frequencies, and that the frequency
of chaotic carriers must as high as of the DC-DC converters. Therefore, if a digital chaotic carrier
were used, the speed of the generating DSP, single-chip or or other computer would be required
to be correspondingly high, resulting in very high cost. Even so, existing processors can hardly
satisfy the practical requirements. Instead, analogue chaotic carriers can be employed, leaving
the problem of how to design them.
Actually, in [57] a design method is proposed using three switches (a main switch and two
auxiliary ones), leading to large switching loss. Moreover, the chaotic generator circuit described
in [57] can generate one kind of chaotic signals, only.
In this chapter, only one switch is adopted in generating a chaotic carrier by porting one of
the numerous existing chaotic oscillator circuits, i.e., Chua’s chaotic oscillator, which renders
the circuit design more flexible. Another contribution of this chapter is to propose a transform
to increase the frequency of the chaotic oscillator to a value required. Then, simulations and
44
5 Analogue Chaotic PWM
experiments will be conducted to verify the effectiveness of the novel analogue chaotic carrier
in suppressing EMI, which refers to conducted EMI here and throughout the dissertation.
5.2
Analogue Chaotic Carrier
Analogue carriers used for DC-DC converters, such as triangle waves and sawtooth waves, are
generated by charging and discharging a capacitor. The proposed chaotic analogue carrier uses
0
the same principle, and employs a chaotic signal vchaos
generated by a chaotic oscillator as
shown in Figure 5.1.
Control part
Main circuit
Li
VCC
VCC
Vlow
R2
SET
VCC
S
Q
Driver
circuit
Ho
vc
R
Comparator
ng
R1
R5
R5’
vc
Q
CLR
R3
vchaos
R4
Comparator
Proportional circuit
v'chaos
Chaotic oscillator
circuit
S7
C6
n
Sum circuit
Vupp
tio
Vu
5.2.1
er
ta
Figure 5.1: A chaotic sawtooth carrier generator
Circuit Design
Di
ss
The circuit diagram of the analogue chaotic carrier is drawn in Figure 5.1, which can generate
both chaotic sawtooth and chaotic triangle waveforms. It is shown in Figure 5.1 that the lower
limit of the chaotic carrier, Vlow , is determined by R1 and R2 , while its upper limit, Vupp , by
0
Vu and vchaos . The latter is obtained from the output voltage vchaos
of the chaotic oscillator
circuit via a proportional modulation. According to the characteristic table of R-S flip-flop
in Table 5.1, the chaotic carrier circuit operates in the following way. Initially, vc is zero and
vc < Vlow < Vupp . Then, R = 1 and S = 0, which result in Qn+1 = 1, the switch S7 turns
on, and C6 will be charged through R5 and R50 by V CC. When vc > Vlow and vc < Vupp , one
has that R = 1 and S = 1. In terms of Table 5.1, it holds Qn+1 = Qn , which means that the
switch remains “on” until vc arrives or exceeds Vupp . When S = 1, R = 0 and Qn+1 = 0, the
switch turns off, and C6 begins to discharge through R50 until vc ≤ Vlow . Thereafter, a new
circle begins.
When R50 is very small or close to zero, C6 discharges very fast, and the output voltage of C6 is
close to be a sawtooth waveform. If R0 is equal to or larger than R, then a triangle waveform
appears. Based on circuit theory, the frequency of the chaotic carrier can be calculated by the
following expression
1
,
(5.1)
fcn =
tncharge + tndischarge
5 Analogue Chaotic PWM
45
Table 5.1: Characteristic table of RS flip-flop
R
0
1
1
0
S
1
0
1
0
Qn+1
0
1
Qn
unstable
Ho
ng
Li
−Vlow
low
where tncharge = −(R5 + R50 )C6 ln(1 − VVupp
) and tndischarge = −R50 C6 ln( VVupp
).
CC−Vlow
In practice, a reference frequency fC always needs to be defined, since the design of inductor
and capacitor in DC-DC converters is based on a certain frequency. In this chapter, fC is
defined as the frequency when Vupp = Vu . Normally, vchaos ∈ (−M, M ), where M is a positive
real number, so that fcn will fluctuate around fC , and the fluctuating range is dependent on
0
vchaos
and the proportional circuit.
Due to the chaotic characteristics of Vupp , fcn = T1n varies chaotically, as shown in Figure 5.2.
Therefore, it is called chaotic carrier.
vc / V
Vupp=Vu+vchaos
tio
er
ta
Vlow
Vupp
n
Vu
vc
vchaos
t / s
Figure 5.2: Chaotic carrier
Di
ss
Tn
5.2.2
Chaotic Oscillator
In recent decades, chaotic oscillators have widely been investigated [8, 14, 17], and are extensively applied in many fields, such as communication security and industrial mixing. Here,
chaotic oscillators are used for the first time in PWM control of DC-DC converters to reduce
EMI.
Among the existing chaotic oscillators, Chua’s, Lorentz’s, and Chen’s oscillators are most well
known. In this section, Chua’s oscillator is adopted due to its simplicity and maturity. Figure 5.3 shows Chua’s oscillator, where NR is Chua’s diode (cp. Figure 5.4), and VR and iR
satisfy the relationship,
1
iR = f (VR ) = Gb VR + (Ga − Gb )(|VR + E| − |VR − E|).
2
(5.2)
46
5 Analogue Chaotic PWM
iR
R
R0
+
+
V2
-
C2
L1
+
V1
-
C1
NR
VR
-
i3
Li
Figure 5.3: Chua’ oscillator circuit
ng
iR
Ho
Gb
E
-E
VR
tio
n
Ga
er
ta
Figure 5.4: Typical iR -VR characteristic of Chua’s diode
Di
ss
Chua’s oscillator can be described by the following differential equations;
 dV1
1
 dt = C1 [(V2 − V1 )G − f (V1 )],
dV2
= C12 [(V1 − V2 )G + i3 ],
 didt3
= − L11 (V2 + R0 i3 ),
dt
(5.3)
where G stands for the reciprocal of Ohm.
For the case R = 1858Ω, R0 = 0Ω, L1 = 18mH, C1 = 10nF , C2 = 100nF , E = 1.075V ,
Ga = −757.58µS, and Gb = −409.09µS the phase portraits of the chaotic oscillator are shown
in Figure 5.5.
It is noted here that when a chaotic oscillator is used for a chaotic carrier, but the frequency of
the existing chaotic oscillators cannot follow the required switching frequency, these oscillators’
frequencies should be increased by adjusting their circuits’ parameters. To maintain the same
chaotic characteristics of these oscillators, the relationship between the parameters and the
frequencies should be found. For Chua’s chaotic oscillator, to increase the frequency of vchua
from fv to N fv , one just needs to apply the transform t = N τ . To this end, the differential
equations (5.4) can be re-written an
 dV
1
1

 dτ = C1 /N [(V2 − V1 )G − f (V1 )],
dV2
= C21/N [(V1 − V2 )G + i3 , ]
(5.4)
dτ

 di3 = − 1 (V + R i ).
2
0 3
dτ
L1 /N
47
Li
5 Analogue Chaotic PWM
(b) Phase portrait of V1 - i3
ng
(a) Phase portrait of V1 - V2
Figure 5.5: Phase portraits of Chua’s oscillator
5.3.1
Analogue Chaotic PWM
A Boost Converter
er
ta
5.3
tio
n
Ho
Consequently, the frequencies of outputs, such as vchaos , will be increased N times when the
parameters C1 , C2 and L1 are replaced by C1 /N , C2 /N and L1 /N . The approach is also
applicable to other chaotic oscillators. However, it is remarked that, in practice, the transformed
parameters should be adjusted by trial and error, because circuit components are normally not
ideal.
Di
ss
Here, an analogue chaotic carrier is to be embedded in a PWM boost converter as shown in
Figure 5.6, because it is one of the basic topologies of DC-DC converters and very popular in
many practical circuits, such as power factor correction (PFC) circuits, power inverters, and so
on. The switch S, the input inductor L, the freewheel diode D, and the output filter capacitor
C constitute the main circuit of the boost converter; while RL representing a resistive load, the
sampling circuit for iL , the reference circuit for Iref , a operational amplifier, a comparator, and
a carrier (periodic carrier or chaotic carrier) form the PWM control part as shown in Figure 5.6.
5.3.2
Simulations
Two different control methods, including traditional PWM, i.e., PWM with periodic carrier,
and chaotic PWM, i.e., PWM with chaotic carrier, are now simulated and compared in terms
of their performance on suppressing ripple and EMI, and improving efficiency.
The circuit diagram of the boost converter is shown in Figure 5.6, where VI = 10V , L = 1mH,
C = 10µF , R = 200Ω and fC = 10KHz. For the control part, Vlow = 0V , Vu = 2V and
Iref = 1A are set.
The periodic carrier can easily be generated as Vupp = Vu = 2V (see Figure 5.1). In order
to generate the chaotic carrier, just assume that the parameters of the embedded chaotic
0
0
oscillator assume the values as given in Section 5.2.2, and V2 = vchaos
. If vchaos
is proportionally
modulated within (−0.3, 0.3), then one has Vupp ∈ (1.7, 2.3). The periodic and the chaotic
carriers generated are shown in Figures 5.7(a) and 5.7(b), respectively.
5 Analogue Chaotic PWM
n
Ho
ng
Li
48
Di
ss
er
ta
tio
Figure 5.6: A PWM boost converter
(a)
(b)
Figure 5.7: Periodic carrier (a) and chaotic carrier (b) with Chua’s oscillator
5 Analogue Chaotic PWM
49
It is remarked that due to the chaotic carrier’s frequency being around 10kHz, the frequency
of Chua’s chaotic oscillator with the above selected parameters should be accelerated 104 times
based on its original frequency, which can be estimated by observing the frequency with biggest
amplitude in its spectrum revealed by fast Fourier transform (FFT). With the transformation
t = 104 τ , the FFT spectrum of Vupp is shown in Figure 5.8. It is obvious that the frequency of
Chua’s oscillator can now catch up with the switching frequency of the boost converter.
20
Li
0
ng
Amplitude
10
Ho
-10
-20
30
40
50
60
Frequency (kHz)
n
20
70
80
90
100
tio
0
10
Frame: 24
Figure 5.8: FFT spectrum of Vupp
Di
ss
er
ta
Comparison results for the output waveforms, the phase portraits, and the input current spectra
of the boost converters under PWM control using the chaotic carrier (Figure 5.7(b)) and the
periodic carrier (Figure 5.7(a)), respectively, are shown in Figures 5.9 – 5.11 and in Table 5.2.
It is remarked that the current and voltage overshoots are almost the same, the current and
voltage ripples increase slightly, the efficiency is improved, and EMI is greatly reduced, when
the periodic carrier is replaced by the chaotic one in the PWM control. In summary, the
chaotic carrier does not change the DC-DC converters’ characteristics, such as the basic output
waveforms and stability, however, it improves EMC considerably according to Figure 5.11,
especially in the low frequency band.
Table 5.2: Performance comparison of the boost converter with different control methods
Parameters for comparison
current
overshoot(A)
voltage
overshoot(V)
current
ripple(A)
voltage
ripple(V)
efficiency(%)
Traditional PWM
Chaotic PWM
1.064
1.053
16.70
16.75
0.2607
0.3404
0.7326
91.78
1.0592
93.45
5 Analogue Chaotic PWM
(a) Waveforms of the traditional boost converter
Li
50
(b) Waveforms of the chaotic boost converter
er
ta
tio
n
Ho
ng
Figure 5.9: Output waveforms of the boost converter
(a) Periodic phase
(b) Chaotic phase
5.4
Di
ss
Figure 5.10: Phase portraits of the input current and output voltage when the boost converter
operates in periodic and chaotic modes
Experiments
To further verify the effectiveness of the analogue chaotic PWM, also an experiment and hardware were designed. First, as the chaotic oscillator’s core, the circuit design of Chua’s diode is
introduced.
5.4.1
Chua’s Diode
So far, many methods have been reported to build Chua’s diode [18], among which the most
popular one is shown in Figure 5.12, and its parameter design is given in [31]. Here, the
parameters for Chua’s diode are chosen as Rd1 = 2.4KΩ, Rd2 = 3.3KΩ, Rd3 = Rd4 = 220Ω,
and Rd5 = Rd6 = 20KΩ.
The other parameters of Chua’s oscillator in the experiment are L1 = 2.2mH, C1 = 4.7nF ,
C2 = 500pF , and R = 1.75KΩ. The parameters for the main circuit of a chaotic sawtooth
generator are Rs = 1KΩ, Rs0 = 3.9Ω, Cs = 22nF , and V CC = 5V . For the main circuit of the
5 Analogue Chaotic PWM
51
40
20
Amplitude
0
-20
-40
-60
-80
-100
0.4
0.6
0.8
1
1.2
Frequency (MHz)
1.4
1.6
1.8
2
Li
0
0.2
Frame: 26
(a) Spectrum of inductor current of hard switching boost converter
ng
40
20
Ho
Amplitude
0
-20
-40
n
-60
-100
tio
-80
0
0.2
Frame: 26
0.4
0.6
0.8
1
1.2
Frequency (MHz)
1.4
1.6
1.8
2
er
ta
(b) Spectrum of inductor current of chaotic hard switching boost converter
Figure 5.11: Spectra of inductor current of the boost converter
Di
ss
boost converter and the PWM control part, assume that VI = 10V , L = 680mH, C = 10µF
and RL = 200Ω; Vlow = 0V , Vu = 2.5V , Iref = 1A, and fC ≈ 60KHz. With these parameter
settings, the boost converter will operate in current continuous mode (CCM) with a duty cycle
of around 40%.
Circuit diagram, printed circuit board, and an experimental board of the PWM boost converter
are shown in Figure 5.15. The boost converter can be induced to operate in periodic or chaotic
mode through jumpers J7 and J8, which have been marked on Figures 5.13 – 5.15.
5.4.2
Experimental Results
The waveforms of periodic and chaotic carrier are given in Figure 5.16, and the output voltages
with ripple measurements of the PWM boost converter with two kinds of carriers are provided
in Figure 5.17.
It is seen from Figure 5.17 that the ripple increases by 120mV as the periodic carrier is replaced
by a chaotic one, while the efficiency of the boost converter is improved from 86.40% to 89.43%.
In this experiment, the EMC standard GB9254-1998 CE (AV class A and QP class A) is applied,
the measurement bandwidth is 9kHz, the frequency step 5kHz, the attenuation 10dB, and the
frequency range 0.15–30M Hz.
The measurement results of the boost converter’s EMI with the periodic and chaotic carriers
52
5 Analogue Chaotic PWM
Chua’s Diode
Rd3
iR
+
A1
Rd4
Rd5
Rd6
ng
Rd2
Ho
Rd1
Li
+ A2
-
Di
ss
er
ta
tio
n
Figure 5.12: Chua’ Diode
Figure 5.13: Circuit diagram of the boost converter
53
n
Ho
ng
Li
5 Analogue Chaotic PWM
Di
ss
er
ta
tio
Figure 5.14: Printed circuit board of the boost converter
Figure 5.15: Experimentation board of the boost converter
5 Analogue Chaotic PWM
ng
Li
54
(b)
Ho
(a)
Di
ss
er
ta
tio
n
Figure 5.16: Periodic carrier (a), and chaotic carrier (b)
(a)
(b)
Figure 5.17: Ripples of the output voltage as the boost converter operates: (a) in periodic
mode and, (b) in chaotic mode
55
ng
Li
5 Analogue Chaotic PWM
Ho
Figure 5.18: EMI of the periodic PWM boost converter
Di
ss
er
ta
tio
n
are given in Figures 5.18 and 5.19, respectively, which show that applying the chaotic carrier
in reducing EMI is much more effective in the low frequency band, which is consistent with the
simulation results.
Figure 5.19: EMI of the chaotic PWM boost converter
5.5
Summary
This chapter is concerned with analogue chaotic PWM, where the key is to design an analogue
chaotic carrier using chaotic oscillators. According to the simulation and experimental results,
although the ripple in the output voltage is slightly increased by adopting the chaotic carrier
instead the periodic one, the efficiency of the boost converter is much improved and the EMI is
distributed much smoother on the frequency band, which allows the boost converter to better
satisfy the EMC standards.
56
6 A Chaotic Soft Switching PWM Boost Converter
Chapter 6
ng
Li
A Chaotic Soft Switching PWM Boost
Converter
Introduction
ss
6.1
er
ta
tio
n
Ho
So far, we have shown that CPWM can suppress EMI significantly by spreading the spectra
over a wide frequency band. Moreover, EMI is mainly caused by rapid di/dt and dv/dt, which
can be reduced by the soft switching technique. Therefore, in this chapter, a novel method
based on CPWM and soft switching control is proposed for the reduction of the EMI in DCDC converters. Here, a digital generator of the chaotic carrier is proposed based on a chaotic
mapping and a sawtooth wave generator, which convert the periodic sawtooth wave into a
chaotic one. Simulation results show that the EMI of the DC-DC boost converter is much
reduced due to the total energy more evenly spreaded over the frequency band and reduced
energy loss. It is also found that the efficiency of the DC-DC boost converter is improved as
compared with the hard and soft switching PWM controls.
Di
Since CPWM control cannot directly reduce the rapid change rate of voltage and current,
another earlier proposed, more popular and practical technique, i.e., soft switching, will be
introduced. The technique of soft switching was first presented in [15] and was rapidly developed
in recent years [19, 21, 65]. The concept is to open and close the switch at zero current or zero
voltage to alleviate the high rates of changes in voltage and current so that EMI can be reduced.
Thus, the switching loss is reduced, which implies that the energy loss is also reduced, resulting
in improved efficiency.
CPWM has been proposed and simulated [7, 37, 50, 69, 70, 72, 75], but there are no hardware
implementations. In addition to the hardware implementation of the analogue chaotic carrier
given in Chapter 5, an implementation of a digital chaotic carrier generated by a sawtooth
generator, whose period length is governed by a chaotic mapping, will be detailed in this
chapter.
Further, this chapter is concerned with combining CPWM with soft switching in order not to
spread the energy distribution over the whole frequency band (thus reducing the peaks in the
spectrum), only, but also to reduce the switching loss or energy loss, such that EMI cannot
only be greatly reduced, but that the efficiency is improved, too.
6 A Chaotic Soft Switching PWM Boost Converter
6.2
6.2.1
57
Circuitry and Control
Circuit Description
er
ta
tio
n
Ho
ng
Li
The chaotic soft switching PWM boost converter is depicted in Figure 6.1, where the switch
S1 , the inductor L1 , the diode D3 , and the capacitor C2 form the main circuit of the boost
converter, and R represents a resistive load. The soft switching of S1 , which was proposed in
[2], is governed by the auxiliary circuit consisting of inductors L2 and L3 , diodes D1 and D2 ,
and capacitor C1 . Usually, the inductances of L2 and L3 are much smaller than that of L1 , and
the capacitance of C1 is much smaller than that of C2 .
Figure 6.1: Chaotic soft switching PWM boost converter
Di
ss
It is possible to classify the operations of the boost converter into seven different modes based
on the principle of soft switching. They are described briefly as follows (cf. [2] for details).
According to [2], Vout and iL1 are assumed as constants V1 and I1 for Modes 1 and 2, and V2
and I2 for Modes 5 and 6, respectively, since iL1 is quite small in Modes 1, 2, 5 and 6.
Mode 1 (t ∈ [t0 , t1 ))
Let the initial values of L2 and L3 be zeros, and C1 previously be charged to a value VC1 (t0 ).
Assume that the switch S1 is turned on when the current is zero at time t0 , while the current
iL2 (t) will then gradually rise and become I1 + iL3 (t) at t1 when D3 turns off.
The equivalent circuit is shown in Figure 6.2(a), and the expressions for iL2 (t), iL3 (t) and VC1 (t)
can be derived as
V1
t,
L2
VC1 (t) = [V1 − VC1 (t0 )][1 − cos ω1 t]] + VC1 (t0 ),
sin ω1 t
iL3 (t) = [VC1 (t0 ) − V1 ]
,
ω1 L3
iL2 (t) =
where ω1 =
√ 1
.
L3 C1
(6.1)
58
6 A Chaotic Soft Switching PWM Boost Converter
ng
Li
(a) mode 1
(c) mode 3
(e) mode 5
er
ta
tio
(d) mode 4
n
Ho
(b) mode 2
ss
(f) mode 6
(g) mode 7
Di
Figure 6.2: Circuits equivalent to the soft switching boost converter in different modes
Mode 2 (t ∈ [t1 , t2 ))
Since D1 is off, the operations of this mode can be represented by the equivalent circuit shown
in Figure 6.2(b). The capacitor C1 is to be completely discharged and VC1 eventually reaches
zero at t2 . Assuming that the initial values of L3 , L2 , and C1 are equal to iL3 (t1 ), iL2 (t1 ) + I1 ,
and VC1 (t1 ), respectively, evaluated at the end of Mode 1, one has
VC1 (t) = −VC1 (t1 )(2 − cos ω2 t) −
iL3 (t1 )
sin ω2 t,
ω2 C1
VC1 (t1 )
sin ω2 t + iL3 (t1 ) cos ω2 t,
ω2 (L2 + L3 )
VC1 (t1 )
iL2 (t) =
sin ω2 t + iL3 (t1 ) cos ω2 t + I1 ,
ω2 (L2 + L3 )
iL3 (t) =
where ω2 = √
1
.
(L2 +L3 )C1
(6.2)
6 A Chaotic Soft Switching PWM Boost Converter
59
Mode 3 (t ∈ [t2 , t3 ))
The equivalent circuit for this mode is shown in Figure 6.2(c), where the initial conditions of
iL2 , iL3 , and VC1 are iL2 (t2 ), iL3 (t2 ), and zero, respectively. From t2 to t3 , the current iL3 (t)
drops and becomes zero at t3 . The expression for iL3 is given by
iL3 (t) =
−VS L2
t + iL3 (t2 ).
L 1 L2 + L2 L 3 + L 3 L 1
(6.3)
Mode 4 ( t ∈ [t3 , t4 ))
iL1 (t) = iL2 (t) =
1
− RC
t
Mode 5 (t ∈ [t4 , t5 ))
2
VS
t + I1 ,
(L1 + L2 )
.
Ho
Vout (t) = V1 e
ng
Li
The equivalent circuit for this mode is shown in Figure 6.2(d). At t4 , the end of this operational
mode, iL1 (t) and Vout (t) attain the values I2 and V2 , respectively, and the switch S1 is turned
off. Hence, one has
(6.4)
tio
n
For this mode, after S1 turns off, the current iL2 (t) drops and reaches zero at t5 . The equivalent
circuit is shown in Figure 6.2(e), where the initial condition of iL2 is I2 . The expressions for
iL2 , iL3 , and VC1 are then obtained as
VC1 (t) = V2 (1 − cos ω3 t) +
I2
sin ω3 t,
ω3 C1
er
ta
L2
[V2 C1 ω3 sin ω3 t − I2 (1 − cos ω3 t)] + I2 ,
L 2 + L3
L2
iL3 (t) =
[V2 C1 ω3 sin ω3 t − I2 (1 − cos ω3 t)],
L 2 + L3
iL2 (t) =
1
ss
q
(6.5)
L2 L3
(L2 +L3 )C1
.
Di
where ω3 =
Mode 6 (t ∈ [t5 , t6 ))
In this mode, the current iL3 decreases and becomes zero at t6 , in terms of the equivalent circuit
given in Figure 6.2(f). The expressions for iL3 and VC1 can be derived as
VC1 (t5 ) − V2
sin ω1 t + iL3 (t5 ) cos ω1 t,
L3 ω1
iL3 (t5 )
VC1 (t) =[VC1 (t5 ) − V2 ][cos ω1 t − 1] −
sin ω1 t.
ω1 C1
iL3 (t) =
(6.6)
Mode 7 (t ∈ [t6 , t7 ))
The last mode is under the conditions of having zero iL2 and zero iL3 . Figure 6.2(g) depicts
its equivalent circuit, which is also the normal mode of the boost converter. At the end of this
mode or at t7 , S1 is turned on at zero current, the inductor current iL1 will reach I1 and Vout
60
6 A Chaotic Soft Switching PWM Boost Converter
will reach V1 . Therefore, one has
Vout (t) = e−αt [A sin ω4 t + B sin ω4 t] + VS ,
Vout (t)
iL1 (t) =
+ e−αt
R
[(−BC2 α + AC2 ω4 ) cos ω4 t
−(AC2 α + BC2 ω4 ) sin ω4 t],
where α =
6.2.2
1
,
2RC2
ω4 =
√ 1
,
L1 C2
A=
I2
ω4 C2
−
V2
Rω4 C2
+
α(V2 −VS )
ω4
(6.7)
and B = V2 − VS .
Chaotic Soft Switching PWM Control
Ho
ng
Li
With traditional PWM control, the carrier frequency fC is invariant and has biggish peaks
close to the carrier frequency or its multiples in the spectrum, making it difficult for the DCDC converters to satisfy the international standards for Electromagnetic Compatibility (EMC).
The problem can be solved by using CPWM control [7, 37, 50, 69, 70, 72], in which a chaotic
carrier is integrated. The reason is that the chaotic carrier can distribute the spectrum continuously and evenly over a wide range of frequencies. Although the total energy may not be
altered, the magnitudes of the peaks are reduced, thus EMI is restrained.
A Digital Chaotic Carrier
Xn-1
er
ta
tio
n
The chaotic carrier to be combined with soft switching can be analogue or digital depending
on the application of interest. The design of an analogue chaotic carrier has been introduced in
Chapter 5 Therefore, this subsection just introduces the design of an applicable digital chaotic
carrier.
xn=u
u.ß.TC + TC
T’nC
Di
ss
Chaotic mapping
Pulse signal
No
Yes
, the given samples
in each period length
Vlow+(Vupp-Vlow)(N-1)/(N-1)=Vupp
Vlow+(Vupp-Vlow)(N-2)/(N-1)
Vlow+(Vupp-Vlow)(N-n)/(N-1)
Vlow+(Vupp-Vlow)/(N-1)
Vlow
T’nC /N
Sawtooth generator
n=N?
Figure 6.3: Generation of chaotic carrier
The diagram of the proposed design is depicted in Figure 6.3, based on a chaotic mapping and
a sawtooth generator. It is remarked that the chaotic carrier is being generated as the DC-DC
converter is running. The period length of the n-th sawtooth signal can be determined by the
following mapping:
0
TnC
= xn βTC + TC , xn ∈ [−1, 1], β ∈ [0, 1),
(6.8)
where TC is the fundamental frequency of the switch, which is a constant, xn is the n-th output
of the chaotic mapping, and β is a modulation factor, which can slightly modulate the trade-off
between ripple and EMI.
6 A Chaotic Soft Switching PWM Boost Converter
61
Here, the chaotic sequence xn is generated by the logistic mapping, which is described as
f (xn ) = 1 − µx2n , x ∈ [−1, 1].
(6.9)
ng
Li
where µ = 2 (at which the largest chaoticity is reached).
Let TC = 10µs, the corresponding periodic and chaotic sawtooth carriers are shown in Figure 6.4
for β = 0.05 and 0.2. It should be emphasised that some other chaotic mappings, such as the
shift mapping or tent mapping, can also be applied.
(b) Chaotic carrier at β = 0.05
tio
n
Ho
(a) Periodic carrier
er
ta
(c) Chaotic carrier at β = 0.2
Figure 6.4: Different carrier waveforms generated according to Figure 6.3
ss
Experiment
Di
The generation process of the chaotic carrier is shown in Figure 6.3 in form of a flow diagram. An
experiment is conducted using a single-chip computer of type C8051F410, which can download
programs from a PC through a USB debug adaptor, as shown in Figure 6.5.
Figure 6.5: Illustration of the hardware connection
Let TC = 0.001s, Vupp = 1.5V , Vlow = 0V , and β = 0.2 and β = 0.5, respectively. After
programming the single-chip computer with the method introduced in Section 6.2.2, the digital
chaotic carrier is obtained as shown in Figure 6.6.
6 A Chaotic Soft Switching PWM Boost Converter
Li
62
(a) β = 0.2
(b) β = 0.5
Simulations and Performance Evaluation
Ho
6.3
ng
Figure 6.6: Digital chaotic carriers for different β
Di
ss
er
ta
tio
n
In this section, the proposed chaotic soft switching PWM boost converter is first simulated. In
order to highlight its merits, then comparisons with hard switching PWM and soft switching
PWM are carried out focusing on their performance in ripple suppression and the improvement
of EMC and efficiency.
The chaotic soft switching PWM boost converter is shown in Figure 6.1, where VS = 10V ,
L1 = 0.6mH, C2 = 10µF , R = 200Ω, Iref = 1A, and TC = 10µs. For the soft switching
control, assume that L2 = L3 = 10µH and C1 = 10nF , while the components L1 , L2 , C1 , D1 ,
and D2 are not necessary for hard switching PWM control.
(a) Inductor current
(b) Output voltage
Figure 6.7: Output waveforms of the boost converter with hard switching PWM
The inductor currents iL1 and output voltages Vout obtained for the three control methods are
shown in Figures 6.7 – 6.10, respectively, and the corresponding power spectral densities (PSD)
of the inductor currents are depicted in Figure 6.11. From this figure it is obvious that even a
very small chaotic disturbance to a sawtooth carrier frequency can greatly improve the EMC.
For ease of comparison, in Table 6.1 the results are compiled. It is observed that the ripples are
similar; however, significant improvements of EMC and efficiency are observed, as compared
with the results for hard and soft switching PWM.
It is also observed that the overshoot of the inductor current is largest for hard switching PWM,
but that its voltage overshoot is smallest. By comparing the results with soft switching and
chaotic soft switching, the current overshoot and the voltage overshoot are found to be almost
the same.
6 A Chaotic Soft Switching PWM Boost Converter
(b) Output voltage
Li
(a) Inductor current
63
tio
n
Ho
ng
Figure 6.8: Output waveforms of the boost converter with soft switching PWM
(b) Output voltage
er
ta
(a) Inductor current
Di
ss
Figure 6.9: Output waveforms of the boost converter with chaotic soft switching PWM at
β=0.05
(a) Inductor current
(b) Output voltage
Figure 6.10: Output waveforms of the boost converter with chaotic soft switching PWM at
β=0.2
64
6 A Chaotic Soft Switching PWM Boost Converter
40
20
Amplitude
0
-20
-40
-60
-80
-100
2
3
4
5
6
Frequency (MHz)
7
8
9
(a) PSD of inductor current with hard switching PWM
40
ng
20
0
-20
-40
Ho
Amplitude
10
Li
0
1
Frame: 13
-60
-80
-100
2
3
4
5
6
Frequency (MHz)
7
8
9
10
n
0
1
Frame: 13
tio
(b) PSD of inductor current with soft switching PWM
40
20
Amplitude
er
ta
0
-20
-40
-60
-80
ss
-100
0
1
Frame: 13
2
3
4
5
6
Frequency (MHz)
7
8
9
10
Di
(c) PSD of inductor current with chaotic soft switching PWM at β =0.05
40
20
Amplitude
0
-20
-40
-60
-80
-100
0
1
Frame: 13
2
3
4
5
6
Frequency (MHz)
7
8
9
10
(d) PSD of inductor current with chaotic soft switching PWM at β =0.2
Figure 6.11: PSDs of inductor currents based on different control methods
6 A Chaotic Soft Switching PWM Boost Converter
65
It should be noticed that the proposed chaotic soft switching PWM control can be tuned
easily. The modulation factor β can be tuned to reach any trade-off performance between
ripple magnitude and EMC. In addition, since a constant TC is used and the chaotic carrier
frequency is close to TC , the system parameters of the DC-DC converter can easily be obtained
according to the standard design procedures for the periodic mode, depending on the switching
frequency. This is particularly obvious for the case that β is very small.
Table 6.1: Performance comparison of the boost converter with three different control methods
chaotic soft
switching PWM
β=0.05 β=0.2
soft switching
PWM
1.2765
-0.216
18.9355
28.05
28.045
28.0532
0.0679
0.0669
0.0783
0.0840
0.0481
87.52
0.0507
91.56
0.1105
91.32
-0.216
ng
Ho
0.0410
78.92
Li
hard switching
PWM
-0.216
6.4
Summary
tio
n
Parameters
for comparison
current
overshoot(A)
voltage
overshoot(V)
current
ripple(A)
voltage
ripple(V)
efficiency(%)
Di
ss
er
ta
A chaotic switching PWM has been proposed in this chapter. It can improve EMI and efficiency
as compared with both hard and soft switching PWM, at the price of a small increase in ripple
magnitude. However, it is noted that this approach leads to a relatively complicated circuit,
increasing cost and size of the final circuit. Fortunately, this problem can be alleviated by the
rapid development of large scale integration.
66
7 Invariant Densities of Chaotic Mappings
ng
Invariant Densities of Chaotic
Mappings
Li
Chapter 7
7.1
Introduction
tio
n
Ho
This chapter is concerned with applying probability analysis to the chaotic mappings employed
in the control of DC-DC converters. A computation method for the invariant density of a chaotic
mapping is proposed by using the eigenvector method, which is to facilitate the accurate design
of the DC-DC converter parameters. Moreover, the power spectral density of the input to a
DC-DC converter and the average frequency of switching are deduced. Finally, some application
examples are given to illustrate the effectiveness of the method proposed.
Di
ss
er
ta
It is known that chaotic motion is an unstable, aperiodic behaviour within a bounded area,
and that its long-term behaviour shows random-like characteristics, which can be studied using
probability theory.
The invariant density is a basic and important characteristic of chaos. For a DC-DC converter,
a one-dimensional mapping can be derived under some reasonable assumptions, which can
then be used to analyse the chaotic behaviour of the DC-DC converter. Several methods were
proposed to calculate the invariant densities of chaotic mappings used for DC-DC converters.
However, these methods have their own drawbacks. For instance, the method presented in [25]
is difficult to realise by computer due to the immense increase of calculation complexity as
the iteration of the mapping advances just slightly. Moreover, this method does not require
the mapping to have a finite number of Markov partitions [38]. The method described in [71]
uses the Frobenius-Perron operator equation to calculate invariant densities. Since it is well
known that very few Frobenius-Perron operator equations of chaotic mappings can be solved
analytically, this method can be applied in a few special cases, only.
In this chapter, a boost converter operating in a chaotic mode is described by a one-dimensional
mapping, based on which the chaotic mapping’s invariant density is then calculated using
the eigenvector method. Comparing the invariant density of the chaotic mapping with its
phase portrait and its bifurcation diagram shows that the method is appropriate to calculate
invariant densities of the chaotic mappings used to control DC-DC converters. Furthermore,
The calculation results can also be used to estimate the power spectral densities of the inputs,
calculate the average switching frequencies of DC-DC converters, and accurately design the
system parameters. Finally, simulation examples will be given to illustrate the effectiveness of
the method.
7 Invariant Densities of Chaotic Mappings
7.2
67
1-D Mapping for a Boost Converter
A one-dimensional mapping describing the behaviour of the boost converter in Figure 7.1 was
given in [25], and has the form of (7.1), with the inductor current i(t) sketched in Figure 7.2:
xn+1 = α(1 − (xn mod 1)),
tn
,
Tc
α=
V̄O
VI
− 1, and tn =
(Iref −in )L
.
VI
n
Ho
ng
Li
where xn =
(7.1)
Di
ss
er
ta
tio
Figure 7.1: Peak current mode controlled boost converter
Figure 7.2: Current waveform iL (t) in a boost converter
For a boost converter, one has α > 0 due to V̄O > VI . It is easy to see by the Lyapunov exponent
that for α > 1 the sequence {x0 , x1 , . . . , xn , . . .} is chaotic within the range [0, α] [35]. The
mapping (7.1) or its normalisation has extensively been studied, most notably by Rényi [41, 60].
It is shown there by the Rényi transformation that the Frobenius-Perron equation — to be
defined in Section 7.3 — has an invariant density ρ(x), which is (1) absolutely continuous with
respect to the Lebesgue measure on the interval [0, α], as well as (2) ergodic and asymptotically
stable [41]. Due to the random-like characteristic of chaos, the eigenvector method derived
from probability theory and to be introduced in Section 7.4 is employed here to calculate the
invariant density of a chaotic mapping.
68
7.3
7 Invariant Densities of Chaotic Mappings
Invariant Density of a Chaotic Mapping
Li
Chaos is a kind of unstable behaviour in a bounded area. Its long-term behaviour shows
random-like characteristics. Thus, it is possible to characterise it with probability theory, using
the invariant densities ρ(x) of chaotic mappings. The term “invariant” means that the number
of orbit points of a chaotic mapping is invariant under the iterations of the mapping [35].
For some simple cases, such as the parabola mapping, it is possible to represent the invariant
densities analytically. But for general cases, calculating ρ(x) requires to employ the PerronFrobenious equation to obtain numerical solutions. The Perron-Frobenious equation is based
on “conservation of quantity” [35]. Figure 7.3 shows a non-linear function, where y has two
inverse images x1 and x2 , namely, y = f (x1 ) = f (x2 ).
ng
f ( x)
∆
∆1
∆2
x2
x
n
x1
Ho
y
tio
Figure 7.3: Mapping of a non-linear function
er
ta
Denote the small neighbourhoods of x1 , x2 , and y as ∆1 , ∆2 , and ∆, respectively, and the
corresponding probability densities as ρ(x1 ), ρ(x2 ), and ρ(y). According to the law of conserving
quantity [35], one has
ρ(y)∆ = ρ(x1 )∆1 + ρ(x2 )∆2 .
(7.2)
ρ(y) =
Di
ss
When ∆1 , ∆2 , and ∆ are small enough, (7.2) can be recast as,
ρ(x2 )
ρ(x1 )
+ 0
,
0
|f (x1 )| |f (x2 )|
(7.3)
where f 0 (x1 ) = ∆∆1 and f 0 (x2 ) = ∆∆2 . If f (x) has more than 2 inverse images, there exist
xi = f −1 (y), i > 2, and (7.3) can be denoted as
X
ρ(y) =
{xi
=f −1 (y)}
ρ(xi )
.
|f 0 (xi )|
(7.4)
This is the so-called Perron-Frobenious equation, on which the calculation of invariant densities
using the eigenvector method can be based.
7.4
Eigenvector Method
For a non-linear function f (x), f : I → I, the interval I can equally be divided into M
segments. If M is large enough, ρ(x) can be regarded as “invariant” in each small interval.
69
Li
7 Invariant Densities of Chaotic Mappings
ng
Figure 7.4: Partial sketch of a chaotic mapping
tio
n
Ho
Then, ρ(x) can be expressed as M discrete values ρ(x1 ), ρ(x2 ), . . . , ρ(xM ) or in vector form
R = [ρ(x1 ), ρ(x2 ), . . . , ρ(xM )] [24].
In Figure 7.4, pi,j is the transition probability of the j-th interval, and the transition probability
matrix is denoted by
p1,1 p1,2 · · · p1,M p2,1 p2,2 · · · p2,M ,
P =
(7.5)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
M,1 pM,2 · · · pM,M er
ta
in which the entries can be derived by

pm,j = (xn − xm )/L,



pm+1,j = (xs − xn )/L,
pm+2,j = (xc − xs )/L,



pi,j = 0 (1 ≤ i ≤ M, i 6= m, m + 1, m + 2).
(7.6)
Di
ss
Thus, it is easy to see that the calculation of the transition probability matrix P is easy as long
as f (x) and M are known. From the definitions of P , R, and the Perron-Frobenious equation,
P and R satisfy the following equality,
P R = R.
(7.7)
It is concluded from (7.7) that R is the eigenvector of P with eigenvalue 1. Thus, the calculation
of the invariant density is reduced to a calculation of the eigenvector of the transition probability
matrix P .
7.5
Invariant Density of the Boost Converter’s Chaotic
Mapping
For the above mentioned boost converter, according to Eqs. (7.1)–7.7, and by dividing the
interval [0, α] into M equal segments, the eigenvector R = [ρ(x1 ), ρ(x2 ), . . . , ρ(xM )] of P , i.e.,
the invariant density of the chaotic mapping, can be calculated. For α assuming different values,
simulation results are presented below.
For α = 1.30, the phase portrait of the mapping is shown in Figure 7.5(a), and the corresponding
bifurcation diagram and invariant density are given in Figures 7.5(b) and 7.5(c). From these
70
7 Invariant Densities of Chaotic Mappings
(b)
(c)
Ho
ng
Li
(a)
n
Figure 7.5: Chaotic mapping (a), bifurcation diagram (b), and invariant density (c) at α = 1.30
er
ta
tio
figures, it is obvious to see that they inosculate quite well. It is remarked that the invariant
density reflects the operating status of the boost converter from a special perspective.
It is seen from Figure 7.5(a) that there are no orbit points in the intervals [0.13, 0.91] and
[1.10, 1.15], corresponding to the zero invariant density in these intervals. Similarly, for the
cases α = 1.52 and α = 2.65, the simulation results are illustrated in Figures 7.6 and 7.7. The
simulation results illustrate the accuracy of the eigenvector method in calculating the invariant
density.
Examples of Applying Invariant Densities
ss
7.6
Di
The invariant density of a DC-DC converter can be used to calculate the power spectral density
of its input, to estimate its average switching frequency, and to accurately design its parameters.
Two examples are given in the following for illustration.
7.6.1
Power Spectral Density of a DC-DC Converter’s Input Current
Consider the boost converter introduced above. The quadratic derivative of its inductor current
depicted in Figure 7.2 is shown in Figure 7.8. According to [25], the inductor current can be
expressed by
V̄O
d2 i
=
−
{δ(t) − δ(t − TC x1 ) + δ[t − TC (1 + bx1 c)] − δ[t − TC (1 + bx1 c + x2 )]
dt2
L
N
−1
N
X
X
bxk c) + xN ] + δ[t − TC (N +
bxk c)]},
+ · · · − δ[t − TC (N − 1 +
k=1
k=1
(7.8)
7 Invariant Densities of Chaotic Mappings
71
ng
Li
where bxc means the round-off number. Employing the following Fourier transformation,
Z t
1
g(u)du G(ω),
g(t) G(ω) ⇒
jω
−∞
(b)
tio
n
Ho
(a)
(c)
Di
ss
er
ta
Figure 7.6: Chaotic mapping (a), bifurcation diagram (b), and invariant density (c) at α = 1.52
(a)
(b)
(c)
Figure 7.7: ´Chaotic mapping (a), bifurcation diagram (b), and invariant density (c) at α = 2.65
72
7 Invariant Densities of Chaotic Mappings
g(t) G(ω) ⇒ g(t − τ ) e−jωt G(ω),
ng
and
Li
Figure 7.8: Quadratic derivative of inductor current
δ(t) 1,
Ho
results in the Fourier transform of the inductor current to be
1
V̄O
lim
[{1 − exp(−jωTC x1 )} + exp(−jωTC [1 + bx1 c]){1 − exp(jωTC x2 )}
2
ω L N →∞ TN
N
−1
X
bxk c])(1 − exp(−jωTC xN )].
(7.9)
+ · · · + exp(−jωTC [N − 1 +
With the denotations
Jn =
0
PN −1
and
1 + bxk c = n − 1 +
er
ta
k=1
tio
k=1
n
A(ω) = −
k=1 bxk c
for n = 1
,
for n > 1
1 + bxn c,
(7.10)
(7.11)
n=1
ss
Tn =
N
X
PN −1
Eq. (7.9) can be re-written as
Di
N
V̄O
1 X −jωTC Jn
A(ω) = − 2 lim
e
{1 − e−jωTC xn }.
ω L N →∞ TN n=1
(7.12)
The power spectral density of the inductor current is defined as |A(ω)|2 .
When ω = mωc , with ωc the clock angular frequency, one has
N
V̄O
1 X
Am = − 2 lim
1 − e−2jπmxn ,
ω L N →∞ TN n=1
(7.13)
where Am stands for the peak values.
According to Birkhoff’s ergodic theory [30], a mapping f , which is an invariant density, satisfies
the relationship,
Z α
N
1 X
n−1
lim
φ(f (x)) =
φ(y)ρ(y)dy.
N →∞ N
0
n=1
(7.14)
7 Invariant Densities of Chaotic Mappings
73
Thus, A˜m , |Am |2 can be expressed by the invariant density ρ(x) as
Z α
Z α
V̄O
2
2
2
sin2πmxdx)2 ],
cos 2πmxdx − 1) + (
] × [(
Ãm = |Am | = [− 2 2
m ωc LhT i
0
0
(7.15)
where
TN
1
= TC (1 + lim
bxn c).
N →∞ N
N →∞ N
hT i = lim
(b) Enlargement of (a)
er
ta
(a)
tio
n
Ho
ng
Li
A comparison of the power spectral densities calculated by (7.13) without using the invariant
density, and by (7.15) using the invariant density is illustrated in Figure 7.9, and shows that
both have almost the same accuracy, but that the calculation with the invariant density takes
much shorter time, because (7.13) includes exponential operations to be calculated N times
with N → ∞; whereas (7.15) just needs a single calculation, since the invariant density is
known.
Figure 7.9: Comparison of (7.13) shown as “+”, and (7.15) shown as “x”
Average Switching Frequency
ss
7.6.2
Di
Chaos control of DC-DC converters cannot only reduce electromagnetic interference of the converters [27, 34, 74], but also reduce their average switching frequencies, which is very important
for reducing switching loss and increasing stability. The average switching frequency can be
calculated with the invariant density.
If the boost converter shown in Figure 7.1 operates properly, one can assume the total increment
of the inductor current ∆i+(total) to be equal to the total decrement of the inductor current
∆i−(total) for a relatively long time, namely, ∆i+(total) = ∆i−(total) as shown in Figure 7.10.
From Figure 7.10, the total time corresponding to the increasing inductor current is (t0 + t1 +
· · · + tN −1 ). Then, the total time corresponding to the decreasing inductor current, tdown , can
be obtained by,
(t0 + t1 + · · · + tN −1 )m1 = tdown m2 ,
(7.16)
¯
where m1 = VLI and m2 = VOL−VI are the rates of increment and decrement of the inductor
current, respectively. Then, tdown can be obtained from (7.16) as
tdown =
m1
1
(t0 + t1 + · · · + tN −1 ) = (t0 + t1 + · · · + tN −1 ),
m2
α
(7.17)
7 Invariant Densities of Chaotic Mappings
Li
74
ng
Figure 7.10: Times of rising and falling inductor current
and the total duration of switching N times is
1
1
)(t0 + t1 + · · · + tN −1 ) = (1 + )(x0 + x1 + · · · + xN −1 )TC .
α
α
Ho
TN = (1 +
(7.18)
Thus, the total number of clock cycles, denoted by L, is
TN
1
= (1 + )(x0 + x1 + · · · + xN −1 ),
TC
α
(7.19)
n
L=
tio
and the total number of switchings is N .
The average switching frequency is defined [22] as,
N
1
N
Rα
= lim
=
.
1
1
N →∞ (1 + )(x0 + x1 + · · · + xN −1 )
N →∞ L
(1 + α )( 0 ρ(x)xdx)
α
(7.20)
er
ta
hsi = lim
ss
To simplify the analysis, let α be an integer larger than 1. By the chaotic mapping, it is easy to
find that ρ(x) = α1 for integers α ≥ 1. Then, the average switching frequency can be obtained
as
2
hsi =
.
(7.21)
1+α
Di
From (7.21), it is obvious that hsi = 1 when α = 1, implying that the boost converter runs
periodically; and hsi < 1 when α > 1. The boost converter will operate in a chaotic mode when
α > 1, by which the boost converter has a low average switching frequency and low switching
loss. Further, as α increases, the average switching frequency decreases.
7.6.3
Parameter Design with Invariant Density
In designing a DC-DC converter, e.g., the boost converter shown in Figure 7.1, one needs know
the value of the reference current Iref . Generally speaking, the values of input and output
voltage are known conditions. According to [25], Iref can be calculated from the formula,
VI Tc
RTc VI3
3
V¯O + V¯O (
− Iref )RVI −
= 0.
2L
2L
(7.22)
Employing the invariant density, one can accurately design the parameters for a chaotic DC-DC
converter. To simplify the calculation, α is restricted to integers between 2 to 10, because the
invariant density is α1 when α takes on integer values larger than 1.
7 Invariant Densities of Chaotic Mappings
75
Denote the quantity of electric charge through the diode D at the n-th time as Q(xn ). Referring
to the Figure 7.2 and using the physical definition of quantity of electric charge, one has
m2 (1 + bxn c − xn )Tc
)(1 + bxn c − xn )Tc ).
2
Using Birkhoff’s ergodic theory and the invariant density, one can obtain
Z α
N −1
1 X
α+1
hT i = lim
Tc (1 + bxn c) = Tc
(1 + bxc)ρ(x)dx =
Tc ,
N →∞ N
2
0
n=0
Q(xn ) = (Iref −
(7.23)
(7.24)
and
Li
Z α
N −1
1 X
1
m2 Tc 2
hQi = lim
Q(x)f (x)dx = Iref Tc −
Q(xn ) =
.
N →∞ N
2
6
0
n=0
(7.25)
ng
Because of
(7.26)
Ho
V¯O
Q̄
, and V¯O = (1 + α)VI ,
I¯D = , Q̄ = hQi, T̄ = hT i, I¯D =
R
T̄
the reference current Iref can be expressed as
(1 + α)2 VI αVI Tc
+
.
(7.27)
R
3L
A comparison of the Iref s calculated by (7.22) and (7.27) using the invariant density, and
determined experimentally, as shown in Figure 7.11, reveals that the estimation of Iref with
the invariant density is much more accurate.
Di
ss
er
ta
tio
n
Iref =
Figure 7.11: Comparison of Iref s obtained by (7.22) (“*”), (7.27) (“x”), and experimentally
(“.”)
7.7
Summary
The invariant density of a one-dimensional chaotic mapping used in the control of DC-DC
converters has been calculated in terms of the eigenvector method in this chapter. Further,
applications of the invariant density have been introduced.
76
8 Stability of a Chaotic PWM Boost Converter
Chapter 8
ng
Li
Stability of a Chaotic PWM Boost
Converter
Introduction
er
ta
8.1
tio
n
Ho
In the previous chapters, a chaotic pulse width modulation (PWM) boost converter has been
proposed to reduce EMI in DC-DC converters, circuit design and simulations have been conducted. Remaining problems such as mean value estimation of state variables for circuit parameter design, ripple estimation of the input current, and stability analysis are addressed in
this chapter. First, a mean value estimation method is proposed, which is used to estimate
the mean values of state variables of chaotic PWM boost converters to facilitate the design
of circuit parameters and the selection of circuit components. Although ripples are slightly
increased when adopting chaotic carriers, DC-DC converters with reduced EMI are still stable
under chaotic PWM control. This chapter provides a theoretic verification of the effectiveness
and practicability of the chaotic PWM DC-DC converters proposed.
Di
ss
Chaotic PWM control has recently been recognised as an effective technology to suppress
electromagnetic interference (EMI) [23, 44, 45, 69, 70, 75], and is used in switched-mode power
supply (SMPS) converters [44, 69, 75] and in motor drives [23, 70]. Literature shows that
previous research was focused on analysing the introduced chaotic signals and the improved
spectra, but ignored some basic problems such as the mean values of inputs and outputs used
for system design and ripple estimation, as well as system stability under chaotic PWM control.
In Chapters 4 and 6, and in [44, 45] chaotic PWM has been proposed to control a boost DCDC converter in order to suppress EMI by applying the continuous power spectrum feature
of chaos to spread the harmonics of DC-DC converters continuously and evenly over wide
frequency ranges. Therein, a chaotic carrier plays a key role in generating chaotic signals,
whose circuit was designed. Simulation results have shown the effectiveness of the technology
proposed. However, the problems of how to estimate the mean value of the input current to
facilitate circuit parameter design and selection of circuit components, of how to calculate the
ripple increment, and of how to analyse stability of chaotic PWM DC-DC converters remain
open. To the best of our knowledge, these problems are addressed here first.
This chapter is organised as follows: Section 8.2 describes the circuit of the chaotic PWM
boost converter; Section 8.3 proposes an estimation method for the mean values of the state
variables, i.e., input current and output voltage, to facilitate parameter design of the control
part; in Section 8.4 only the ripple of the input current is estimated, since this chaotic PWM
control is a kind of current mode control; finally, in Section 8.5.2, the stability of the chaotic
PWM boost converter is analysed.
8 Stability of a Chaotic PWM Boost Converter
77
Ho
ng
Li
(a) Main circuit of boost converter
(b) Chaotic PWM control
Chaotic PWM Boost Converters
tio
8.2
n
Figure 8.1: Chaotic PWM boost converter
f (xn ) = 1 − µx2n , x ∈ [−1, 1],
(8.1)
Di
ss
er
ta
The chaotic PWM control proposed in Chapter 4 can be used for many kinds of SMPS converters. Here, a boost converter with chaotic PWM control is adopted as test-bed due to its
simplicity and wide application. The main circuit and control part of the boost converter are
shown in Figure 8.1. The difference to traditional PWM lies in the fact that the periodic carrier
is replaced by a chaotic one, whose frequency is determined by a chaos mapping.
Here, the logistic mapping is employed to generate chaotic sequences, which is described by
with µ = 2, where the largest chaoticity is reached.
The circuit parameters are the same as the ones used in Chapter 6, i.e., VI = 10V , L = 6e−4H,
C = 1e − 5F , R = 200Ω, Iref = 1A, and TC = 1e − 5s.
8.3
Estimation of the Mean State Variables
Estimation of the mean state variables is of significance to facilitate proper design of the system
parameters.
To obtain the mean values of input current iL and output voltage uC , first, the output voltage
is assumed to be a constant V¯O for the big output filter capacitance C, and the input current’s
chaotic waveform is regarded to be equivalent to periodic waveforms in terms of the same mean
value, as shown in Figure 8.2.
Denote the mean clock cycle as T̄ , then V¯O can be estimated by assuming that S is switched on
for a time D̄T̄ within the mean clock cycle T̄ , where D̄ is the mean duty cycle of S. Therefore,
78
8 Stability of a Chaotic PWM Boost Converter
Equivalent periodic input current
waveform
Chaotic input current waveform
Imax
Same mean values
IL
ΔIL
iL
DT
Li
T
Rising slope = VI/L and falling slope = (VO-VI)/L
Rising slope = VI/L and falling slope = (VO-VI)/L
ng
Figure 8.2: Sketch of equivalent input currents
V¯O is estimated by
er
ta
tio
n
Ho
¯
∆i
V¯O = R(1 − D̄)(Imax −
),
(8.2)
2
where R is the load resistance, Imax is the maximum value of the equivalent periodic input
current, and ∆IL is the ripple of the equivalent periodic input current (refer to Figure 8.2).
The equation implies that the current through the diode is either zero (for the time D̄T̄ ) or
Imax − ∆IL /2 (for the time (1 − D̄)T̄ ). As S is switched on, iL rises at a rate of VLI for a time
¯
D̄T̄ , while as S is switched off, iL falls at a rate VOL−VI for a time (1 − D̄)T̄ [25].
Since the chaotic carrier can be equivalent to a periodic carrier with period T̄ in terms of
equivalence of the mean input current IL , one has
A(Iref − Imax ) = Vlow +
(Vupp − Vlow )
D̄T̄ ,
T̄
(8.3)
ss
where A is the amplification coefficient.
Here, assuming A = 1 and Vlow = 0, one has
Iref − Imax = Vupp D̄.
(8.4)
Di
In terms of the mean input current increment ∆i¯L+ and decrement ∆i¯L− , it is easy to obtain
that
VI
V¯O − VI
∆i¯L+ = D̄T̄ , ∆i¯L− =
(1 − D̄)T̄ ,
L
L
and ∆i¯L+ = ∆i¯L− = ∆IL .
(8.5)
Eliminating ∆i¯L+ , ∆i¯L− , ∆IL , Imax , and D̄ from (8.2), (8.4), and (8.5) yields
VI T̄
VI T̄
3
V¯O + VI R(Vupp +
− Iref )V¯O − VI2 R(Vupp +
)=0
2L
2L
(8.6)
It is obvious that the mean output voltage and mean input current can be obtained if T̄ is
known, which is determined by the corresponding chaotic mapping.
In chaotic PWM control, each period length of the chaotic carrier is determined by
Tn = xn βTC + TC , n = 1, 2, 3, ...
(8.7)
8 Stability of a Chaotic PWM Boost Converter
79
where xn is the output of the logistic mapping.
Thus, the mean period of the carrier can be expressed as
N
N
1 X
1 X
T̄ = lim
Tn = TC + βTC lim
xn .
N →∞ N
N →∞ N
n=1
n=1
(8.8)
Li
Now, the problem remaining is to derive (8.8), which can be addressed by using the ergodicity
of the invariant density ρ of the mapping f in terms of Birkhoff’s ergodic theory [36]. Given
an expanding mapping f , which preservers the ergodic measure with density ρ(x) on (−1, 1),
one has
Z 1
N
1 X
[n−1]
φ(y)ρ(y)dy.
(8.9)
φ(f
(x)) =
lim
N →∞ N
−1
n=1
For the logistic mapping the invariant density can easily be obtained analytically [36] as
N
ng
1
ρ(x) = √
.
π 1 − x2
Substituting (8.9) and (8.10) into (8.8) yields
(8.10)
ss
er
ta
tio
n
Ho
1 X
T̄ = TC + βTC lim
xn
(8.11)
N →∞ N
n=1
Z 1
1
= TC + βTC
x √
dx = TC .
2
−1 π 1 − x
Now, substituting T̄ = TC into (8.6), one obtains V¯O . It follows that D̄ = 1 − VV¯OI , Imax =
Iref − Vupp D̄, ∆i = VLI D̄T̄ , and the mean input current IL = Imax − ∆I2 L can thus be derived.
Table 8.1 shows the mean input currents and output voltages obtained by the estimation
method outlined above and by circuit simulation based on Simulink with various input voltages
and values for β. The table indicates that β does not contribute to the mean values of the
state variables when the logistic mapping is employed to generate chaotic sequences, which is
consistent with the results of estimation and simulation. It is also remarked that the differences
between estimation and circuit simulation are caused by circuit components.
Di
Table 8.1: Mean values of state variables obtained by estimation and simulation
VI
VI
VI
VI
Parameters
for comparison
= 10V β = 0.05
= 10V β = 0.2
= 12V β = 0.05
= 12V β = 0.2
Mean state variables obtained by
estimation method
circuit simulation
¯
IL
VO
IL
V¯O
0.1156A 15.2056V 0.1193A 15.4467V
0.1156A 15.2056V 0.1192A 15.4402V
0.1348A 17.9850V 0.1398A 18.3172V
0.1348A 17.9850V 0.1397A 18.3107V
The above proposed estimation method is also applicable to other chaotic mappings, although
the invariant densities of some chaotic mappings might not be obtained analytically. Fortunately, a numerical method to solve for invariant densities has been reported in [25, 46].
The estimation results of the mean state variables are very helpful in practice to choose the
circuit components, because different currents are allowed for different components. Further,
(8.6) appearing in the estimation method can be used to design the parameters in the control
part: normally, VI , V¯O , R, and TC are given, therefore, Iref and Vupp can be obtained if any one
is given.
80
8.4
8 Stability of a Chaotic PWM Boost Converter
Feedback variable
Ripple Estimation of the Input Current
It is known from Chapters 4 and 6, that chaotic PWM control can greatly suppress EMI. In
doing so, it causes the ripples of input current and output voltage to increase. Since ripple is
Chaotic PWM waveform
an important index of SMPS converters, it is of significance to know how much the ripples will
be increased.
As current mode control is adopted in this chapter, the ripple of the current will be estimated.
The output waveforms of chaotic PWM control are shown in Figure 8.3.
Li
Chaotic carrier
In+2
In
In+3
ng
In+1
I’n+2
I’n
I’n+3
tn+3
tn+2
Tn+2
Tn+3
Tn+1
PWM signal
tio
n
Tn-1
tn
tn+1
Tn
Ho
I’n+1
Iref - iL
er
ta
Figure 8.3: Output waveforms for chaotic PWM control
It is known that the rising slope of iL is VI /L, and the falling slope is
terms of Figure 8.3, one has
In = Iref − iLn ,
V¯O −VI
.
L
Therefore, in
(8.12)
Di
ss
where iLn means the input current at any moment when S turns on, and
In0 = In −
VI
tn .
L
(8.13)
In terms of the control part, one has
In0 =
Vupp
tn .
Tn
(8.14)
Eliminating In0 from (8.13) and (8.14) yields
tn =
In
VI
L
+
Vupp
Tn
.
(8.15)
Substituting (8.15) into (8.14) results in
In0 =
In
Vupp
(V
).
Tn LI + VTupp
n
(8.16)
81
Li
8 Stability of a Chaotic PWM Boost Converter
(b) by circuit simulation
ng
(a) by iteration method
Ho
Figure 8.4: Estimation of input current iL
Then, the current mapping can be derived from Figure 8.3 and (8.12) – (8.16),
V¯O − VI
(Tn − tn )
L
Vupp V¯O − VI
V¯O − VI
=(
)tn +
Tn
−
Tn
L
L
V¯O − VI
Vupp V¯O − VI
In
+
=(
)V
Tn ,
−
Vupp
I
Tn
L
L
+
L
T
(8.17)
tio
n
In+1 = In0 +
n
Di
ss
er
ta
Due to the complexity of the chaotic mapping (8.17), it is impossible to obtain an analytical
representation of the input current ripple. Instead, it has to be determined numerically.
By observing the maximum of In and the minimum of In0 within 1000 or more iterations, the
ripple can be obtained approximately by max(In ) − min(In0 ).
Here, let (8.17) and (8.16) iterate 1000 times with the initial values I0 = Iref − Imax and
x0 = 0.625. Then, the input current iL can be drawn according to the iteration, as shown in
Figure 8.4(a). Figure 8.4(b) shows the resulting input current when simulating the circuit with
the same parameters as used in the above iteration. It is seen in Figure 8.4 that their ripples
are very close.
Table 8.2 shows the ripple of the input currents obtained by iteration and circuit simulation
with various selections of β and input voltage VI , and the corresponding increments of the
ripples in chaotic mode and in periodic mode (i.e., β = 0).
Normally, the output voltage ripple is not allowed to exceed 1% of the output voltage. It is
seen from Table 8.2 that, although the current ripple seems to increase somewhat, the ripple of
the output voltage is still very small, which can be estimated by multiplying the input current
ripple with the equivalent series resistance (ESR). For instance, as VI = 10V and β = 0.2, the
ripple of the output voltage is only 0.48% of the latter.
Moreover, based on ripple estimation, the relationship between input current ripple and β
is illustrated in Figure 8.5. It is obvious that as β grows, the input current increases as
shown with the “black line” in Figure 8.5, which can be fitted with the polynomial ripple =
−0.0469β 2 + 0.1084 β + 0.0559 as shown with the “red line” in Figure 8.5.
Therefore, the ripple can be calculated from β directly, which is an easy way to estimate ripple
in practice.
82
8 Stability of a Chaotic PWM Boost Converter
Table 8.2: Comparison of input current ripples obtained by iteration method and circuit simulation, and ripple increments
Ripple with
β=0
0.0571A
0.0571A
0.0664A
0.0664A
Ripple
increment
0.0047A
0.0184A
0.0057A
0.022A
er
ta
tio
n
Ho
ng
Li
VI
VI
VI
VI
Parameters
= 10V β = 0.05
= 10V β = 0.2
= 12V β = 0.05
= 12V β = 0.2
Ripple obtained by
iteration simulation
0.0618A
0.0618A
0.0753A
0.0755A
0.0722A
0.0721A
0.0884A
0.0884A
Figure 8.5: Relationship between β and ripple
Stability
8.5.1
Two Operation Modes of the Boost Converter
ss
8.5
Di
A boost converter has two operation phases or two switching modes: when the switch S is
turned on, the state equation refers to Mode I, described by (8.18) and shown in the upper
part of Figure 8.6, and when the switch S is turned off, the state equation refers to Mode II,
described by (8.19) and shown in the lower part of Figure 8.6.
duC
1
= − RC
uC
Mode I didtL
(8.18)
1
= − L VI
dt
Mode II
duC
dt
diL
dt
1
= − RC
uC + C1 iL
= − L1 uC + L1 VI
(8.19)
Assume that the mean duty cycle of S is D̄, the mean state equations can be obtained by
applying state space averaging [51, 64] to (8.18) and (8.19),
duC
1
= − RC
uC + 1−CD̄ iL
dt
(8.20)
diL
1−D̄
1
=
−
u
+
V
C
I
dt
L
L
8 Stability of a Chaotic PWM Boost Converter
83
Figure 8.6: The two operation modes of the boost converter
Li
From (8.20), the output voltage uC and the input current iL in the steady state can be obtained
as follows,
8.5.2
ng
V¯O = VI /(1 − D̄)
¯O
IL = (1−VD̄)R
(8.21)
Ho
(
Stability
er
ta
tio
n
First, it is assumed that every transition state in starting up the converter is supposed to be a
“quasi-steady state”. The state variables slowly increase in the start-up transition and, finally,
reach their own values of the “complete steady state”. So, it seems reasonable to assume the
“quasi-steady state” in the start-up transition. Secondly, suppose that the duty ratio changes
from cycle to cycle, i.e., D̄(t) = D̄(t)+∆D̄, where D̄ is the duty cycle of the “quasi-steady state”
and ∆D̄ is a super-imposed variation. With the corresponding disturbance, the load resistance
R(t) = R + ∆R, the input voltage VI (t) = VI + ∆VI , the input current IL (t) = IL + ∆IL , and
the output voltage V¯O (t) = V¯O + ∆V¯O , the basic equations become
d∆V¯O
dt
d∆IL
dt
¯
¯
(1−D̄)∆IL −IL ∆D̄
C
V¯O ∆D̄−(1−D̄)∆V¯O
∆VI
+ L
L
VO −VO ∆R
= − R∆
+
RC(R+∆R)
=
(8.22)
ss
(
Di
in which the second-order terms of (8.22) have been neglected. Since chaotic PWM control is a
current mode control, the Laplace transform of (8.22) leads to an expression for the disturbance
of the input current of the form,
(R2 LCs2 + RLs + R2 (1 − D̄)2 )∆IL (s)
= (R2 V¯O Cs + RV¯O + R2 IL (1 − D̄))∆D̄(s)
− V¯O (1 − D̄)∆R(s) + (R2 Cs + R)∆VI (s)
(8.23)
Similarly, according to the control part, there are Iref − (Imax + ∆Imax ) = Vupp (D̄ + ∆D̄),
IL + ∆IL = (Imax + ∆Imax ) − (IL∆ + ∆IL∆ )/2), and i∆ + ∆i∆ /2 = (VI + ∆VI )(D̄ + ∆D̄)T̄ /L,
thus ∆IL = − VuppL+VI T̄ ∆D̄ − D̄LT̄ ∆VI , and ∆D̄(s) = −k1 ∆IL (s) − k2 ∆VI (s), k1 , k2 ∈ (0, +∞),
where k1 and k2 are the feedback gains of the control circuit. Then, the disturbance of the
input current can be re-written as:
∆IL (s) =
GV (s)
GR (s)
∆R(s) −
∆VI ,
1 + k1 G(s)
1 + k1 G(s)
(8.24)
84
8 Stability of a Chaotic PWM Boost Converter
where
(1 − D̄)2 IL
,
RLCs2 + Ls + R(1 − D̄)2
(RC − k2 RC V¯O )s + 1 − 2k2 V¯O
GV (s) =
,
RLCs2 + Ls + R(1 − D̄)2
GR (s) =
and
RC V¯O s + 2V¯O
.
RLCs2 + Ls + R(1 − D̄)2
Therefore, the characteristic equation can be obtained as
G(s) =
(8.25)
Li
1 + k1 G(s) = 0
and (8.25) can be further written as
(8.26)
ng
RLCs2 + (L + k1 RC V¯O )s + R(1 − D̄)2 + 2V¯O = 0.
Di
ss
er
ta
tio
n
Ho
It is well known that the root locus of the characteristic equation can be used to judge the
stability of a system [61]. If all roots, obtained when k1 increases from 0 to infinity, distribute
on the left plane, then the system will be stable. The root locus of (8.26) is shown as Figure 8.7.
Figure 8.7: Root locus of characteristic equation (8.26)), k1 ∈ [0, +∞)
According to the root locus of characteristic equation (8.26), the boost converter is stable
for k1 > 0. Furthermore, according to the control part, one has k1 = VuppL+VI T̄ . Therefore, the
difference between chaotic PWM control and traditional PWM control lies in T̄ . For traditional
PWM control as well as for chaotic PWM control using the logistic mapping it holds T̄ = TC .
If other chaotic mappings are employed, it holds always T̄ > 0, implying that k1 > 0. In
summary, the boost converter is stable under this kind of chaotic PWM control.
8.6
Summary
The chapter has addressed estimating the mean values of state variables and the ripples for
chaotic PWM DC-DC converters, which are significant for their design. Finally, the stability
of DC-DC converters under CPWM control has been verified.
9 Chaotic Spectra Analysis Using the Prony Method
85
Chapter 9
ng
Li
Chaotic Spectra Analysis Using the
Prony Method
9.1
tio
n
Ho
It is well known that chaotic DC-DC converters are mainly used to reduce EMI, which is
estimated by its spectrum. Conventionally, the Fast Fourier Transform (FFT) is used to analyse
the spectra. However, it is not applicable to the inner-harmonics, i.e., the non-integral multiples
of the fundamental frequency, which is a prominent feature of chaotic signals. In this chapter,
the Prony method is suggested for spectral estimation of chaos-controlled DC-DC converters.
Numerical simulations show its advantages over the traditional FFT.
Introduction
Di
ss
er
ta
Traditionally, the strength of EMI is measured by estimating the system harmonics, namely, by
deriving the power spectral density (PSD) based on FFT [49]. This spectral analysis approach is
computationally efficient and, in most cases, can provide reasonable results for signal processes.
It has, however, some drawbacks. The most prominent one is that of frequency resolution, i.e.,
the ability to distinguish the spectral responses of two or more signals. The frequency resolution
measured in Hertz is roughly the reciprocal of the time interval in seconds, over which sampled
data are available. The second shortcoming is due to the implicit windowing of the data
that occurs when processing by FFT. Windowing manifests itself as “leakage” in the spectral
domain, i.e., energy in the main lobe of a spectral response “leaks” into the side-lobes, obscuring
and distorting other nearby spectral responses being present [54]. These two drawbacks limit
the application of FFT in analysing short sampled data sequences, which occur frequently in
practice, because many process measurements are short in duration or have slowly time-varying
spectra that are often considered as constant in short sampling intervals. Further, FFT cannot
efficiently estimate inner-harmonics, since it assumes the harmonics to be integral multiples of
the fundamental frequency [47].
To alleviate the limitations of FFT, several new modern spectral estimation methods have been
proposed [39, 53, 56, 63, 68]. In this chapter, one of the available spectral estimation methods,
the Prony method, is employed to investigate and analyse chaotic signals [43, 68]. The Prony
method improves the frequency resolution and is not affected by windowing. Thus, the Prony
method cannot only be applied to spectral estimation, but also to obtaining information about
amplitudes, phases, frequencies, and damping factors of harmonics. Furthermore, it is shown
that the Prony method can be used to reconstruct or to fit sampled data. Finally, some
simulation results are presented for illustration.
86
9 Chaotic Spectra Analysis Using the Prony Method
9.2
Prony Method
Consider N complex sampled data, x(0), x(1), . . . , x(N − 1), which can be fitted by using P
polynomial exponential functions:
x̂(n) =
P
X
bk zkn , n = 0, 1, . . . , N − 1,
(9.1)
k=1
bk = Ak ejθk ,
(9.2)
zk = e(αk +j2πfk )∆t ,
(9.3)
ng
Li
where x̂(n), n = 0, 1, . . . , N − 1, are the fitted data, θk the phase, ∆t the sampling period, Ak
the amplitude, αk the damping factor, and fk the frequency. Traditionally, the fitting problem
is based on minimising the sum of squared errors between measured data x(n) and fitted values
x̂(n):
N
−1
X
ε=
|x(n) − x̂(n)|2 .
(9.4)
Ho
n=0
n
However, it is very difficult, if not impossible, to derive the coefficients {Ak , αk , fk , θk } due to the
existence of the exponential terms, which require to solve a complicated non-linear problem.
Thanks to the Prony method, one can convert this problem to deriving the homogeneous
solution of a constant-coefficient linear difference equation of the form [66]:
ak x̂(n − k),
tio
x̂(n) = −
P
X
(9.5)
k=1
er
ta
by defining the polynomial that has the exponents zk as its roots
F (z) =
P
Y
(z − zk ) = (z − z1 )(z − z2 )...(z − zP )
k=1
ss
=
P
X
ak z P −k , a0 = 1.
(9.6)
k=0
Di
Denote e(n) = x(n) − x̂(n). Then (9.5) can be written as
x(n) = −
P
X
ak x(n − k) +
k=1
Define
u(n) =
P
X
ak · e(n − k), a0 = 1.
(9.7)
k=0
P
X
ak · e(n − k), a0 = 1,
(9.8)
k=0
then, (9.8) can be recast as
x(n) = −
P
X
ak x(n − k) + u(n).
(9.9)
k=1
Here, x(n) is regarded as the output of the P -th order autoregressive (AR) model driven by
noise u(n). Minimising the quadratic sum of u(n) results in the parameter ak (k = 1, 2, . . . , P )
9 Chaotic Spectra Analysis Using the Prony Method
87
[43]. Substituting ak (k = 1, 2, . . . , P ) into (9.5), one can obtain the polynomial equation (9.10),
whose roots are zk (k = 1, 2, . . . , P ), which can easily be calculated by using Matlab,
P
X
ak zkP −k = 0.
(9.10)
k=0
Further substituting zk (k = 1, 2, . . . , P ) into (9.3) yields the frequency fk and the damping
factor αk ,
fk = arctan[Im (zk )/Re (zk )]/2π∆t,
k = 1, 2, . . . , P,
(9.11)
αk = ln|zk |/∆t,


where V = 

1
z1
..
.
1
z2
..
.
...
...
..
.

1
zP
..
.
z1N −1 z2N −1 . . . zPN −1
least-square equation (9.12) gives


,







 , and x = 


Ho

V b = x,

b1
 b2

b =  ..
 .
bP
ng
Li
where Im (∗) and Re (∗) denote the imaginary part and the real part of complex numbers.
Replacing the fitted data x̂(n) by the sampled data x(n) in (9.1)) results in the matrix equation,
x(0)
x(1)
..
.
x(N − 1)



 . Solving the

(9.13)
tio
n
b = (V H V )−1 V H x,
(9.12)
er
ta
in which V H stands for the conjugate transpose matrix of V .
Finally, in terms of (9.2), the amplitudes Ak and the phases θk are obtained as
Ak = |bk |,
k = 1, 2, . . . , P.
θk = arctan[Im (bk )/Re (bk )],
(9.14)
Di
where
ss
Thus, x̂(n) (n = 0, 1, . . . , N − 1) are obtained and denoted in vector form as x̂.
Denote the Fourier transform of x̂ by X̂(f ). Then, the PSD of the N sampled data (P̂P rony (f ))
can be expressed as
P̂P rony (f ) = |X̂(f )|2 ,
(9.15)
X̂(f ) =
P
X
k=1
9.3
Ak ejθ
2αk
.
|αk | + (2π(f − fk ))2
2
Deriving the Power Spectral Density
It is known that the frequency resolution of FFT is proportional to 1/N ∆t, where ∆t is the
sampling period. DC-DC converters always work at high frequencies, so that the sampling
period must be very small. Thus, the resolution of FFT is not satisfactory in practice. In
addition, for the case of short data sequences, e.g., for data obtained in failure diagnosis, where
N is small, the resolution of FFT is also very low.
The Prony method overcomes these drawbacks, at the price that its computation is a little bit
more complex than that of FFT. It can be used to estimate the PSD of DC-DC converters,
especially when converters work in chaotic mode.
88
9 Chaotic Spectra Analysis Using the Prony Method
To show the effectiveness of the Prony method in improving the frequency resolution of the
PSD as compared with that of the FFT, the periodic signal equation below is taken as an
example to derive its PSD with the two methods, respectively:
y(t) = sin(2πf1 t) + 0.6 cos(2πf2 t) + 2 sin(2πf3 t),
(9.16)
Ho
ng
Li
where f1 = 100Hz, f2 = 98Hz, and f3 = 25Hz. Let N = 128 be the number of data sampled,
and fs = 1000Hz the sampling frequency.
n
Figure 9.1: PSD obtained by using the Prony method
tio
Figure 9.1 shows the PSD plot, and the related coefficients derived for P = 10 are given in
Table 9.1.
er
ta
Table 9.1: Coefficients derived for P = 10
Di
ss
Ak
5.97E-38
2.58E-12
2.58E-12
1
1
0.5
0.5
0.3
0.3
4.21E-09
fk
500
467.34
-467.3
25
-25
100
-100
98
-98
0
αk
654.48
26.938
26.938
-2.09E-10
-2.09E-10
3.09E-06
3.09E-06
2.46E-06
2.46E-06
-1106.9
θk
-3.1416
0.6876
-0.68759
-1.3982
1.3982
-0.88027
0.88027
0.67671
-0.67671
-3.1416
Investigating Ak and fk in Table 9.1, it can be seen that by discarding the negative frequencies
and those corresponding to small values of Ak , only three positive frequencies, i.e., f = 25Hz,
f = 100Hz, and f = 98Hz, remain. This is consistent with Eq. (9.16). Further investigating
the damping factors αk , it is noted that the three damping factors corresponding to the three
positive frequencies are very small, implying that the corresponding signals in the polynomial
exponential function (9.1) are periodic, while the others with big damping factors are constant.
In addition, the Prony method can be employed to reconstruct the sampled data of the signal
y using the obtained parameters Ak , fk , αk , and θk as shown in Figure 9.2. It can be seen in
Figure 9.3 that the error between the real signal and the reconstructed one is very small, viz.,
of the order of 10−9 .
9 Chaotic Spectra Analysis Using the Prony Method
Figure 9.3: Error signal
Li
Figure 9.2: Reconstructed signal
89
er
ta
tio
n
Ho
ng
For comparison purposes, FFT is adopted, whose frequency resolution is ∆f = fs /N =
7.8125Hz [48]. This means, if |f1 − f2 | ≤ ∆f , FFT is not able to distinguish these two frequencies. It is shown in Figure 9.4 that using FFT only two peaks are identified, at f1 = 23.4375Hz
and f2 = 101.5625Hz, respectively.
Figure 9.4: PSD obtained by using FFT
Di
ss
It is remarked that although the FFT method is simple and computationally effective, its
frequency resolution is low, especially for short sampled data sequences. In contrast, the Prony
method has its merits in improving frequency resolution and data reconstruction. In particular,
due to the existence of rich inner-harmonics and random-like behaviour in chaotic systems, the
Prony method is more powerful and effective than the FFT method.
9.4
Chaotic Spectral Estimation of DC-DC Converters
It is known that DC-DC converters produce electromagnetic interferences and, thus, electromagnetic pollution. With the increasing use of electronic equipment, the problem of EMI has
attracted increasing attention from engineers [4, 10, 16]. Recently, studies have shown that DCDC converters have broadband spectra when they operate in chaotic modes, and the energy
of EMI is more evenly distributed on the frequency band [27]. Thus, the peak values of EMI
can be decreased, but rich inner-harmonics are generated. The inner-harmonics may result in
quality degradation of the transmission energy, increase of power loss, reliability degradation
of the converter systems, etc. [12, 42]. Thus, it is of significance to detect the inner-harmonics
in the control systems.
9 Chaotic Spectra Analysis Using the Prony Method
ng
Figure 9.5: Ccurrent-controlled boost converter
Li
90
Di
ss
er
ta
tio
n
Ho
As traditional FFT can only detect the fundamental frequency and its integral multiples, it is
not applicable for this case of inner-harmonics. Instead, the Prony method is employed here
for the spectral estimation of the inductor current of a basic DC-DC converter, viz., the boost
converter, whose circuitry is shown in Figure 9.5. Therein, the reference current Iref serves
as the control parameter. By adjusting the reference current, the boost converter can exhibit
period-1, period-2 and chaotic oscillations. In the sequel, the Prony Method is used for spectral
estimation of the inductor current corresponding to the three operating modes.
Assume the circuit parameters to be Vin = 10V , L = 1mH, C = 12µF , R = 20Ω, and
fc = 10kHz, where Vin is the input voltage, L the input inductance, C the output capacity, R
the load resistance, and fc the clock frequency, which lead the converter to operate in continuous
current mode (CCM).
In the simulation, 128 sampled data, in (n = 0, 1, . . . , 127) are taken from the input end
of inductor current. It is shown that the system exhibits period-1 behaviour for Iref = 1A
(Figure 9.6), period-2 behaviour for Iref = 1.8A (Figure 9.7), and chaotic behaviour for Iref =
4A (Figure 9.8).
Figure 9.6: Sampled current
waveform for Iref = 1A
Figure 9.7: Sampled current
waveform for Iref = 1.8A
Figure 9.8: Sampled current
waveform for Iref = 4A
In order to carry out the spectral estimation, we assume that Iref = 1A corresponding to the
period-1 mode and P = 40, which is an empirical value. Using the Prony method introduced
in Section 9.2, the coefficients can be derived as given in Table 9.2 by omitting the negative
frequencies.
It is seen from Table 9.2 that the direct current (DC) component 0.88179A with zero values
of fk and the alternating current (AC) components with non-zero values of fk can be decomposed. That is, by investigating fk , one cannot only distinguish the fundamental frequency and
its integral multiples but also the inner-harmonics. By observing Ak it is known that the amplitude of the fundamental frequency component is the largest one among all AC components.
9 Chaotic Spectra Analysis Using the Prony Method
91
Table 9.2: Parameter values derived for P = 40
Li
θk
3.95E-17
-0.21988
0.39381
0.34639
-0.68313
1.5196
-1.6553
2.6354
-1.2549
-2.4941
-0.8473
-1.2301
-1.9439
0.12254
-2.9312
1.4145
-2.5208
1.24E-19
-2.609
-2.1129
2.6193
ng
αk
23.547
-5102.4
19.932
-4704.9
-358.21
-4605.4
14.556
-5040
10.724
-5306.1
5.6684
-5582
-92.27
-6200.1
3.0246
-6989.8
1.138
0.060618
-6929.6
0.096451
-7176.4
n
Ho
fk
1.00E+05
95246
90000
85613
79998
75738
69998
65823
60000
55824
50002
45704
40000
35518
30000
25385
20000
0
5085.9
10000
15281
Di
ss
er
ta
tio
Ak
0.0015954
1.35E-05
0.0011592
2.38E-05
0.00013856
3.13E-05
0.0014441
4.96E-05
0.0024704
6.79E-05
0.0022907
8.80E-05
0.0002811
0.00012273
0.0056313
0.00019746
0.017208
0.88179
0.0010786
0.048575
0.00034827
(a)
(b)
Figure 9.9: PSD obtained by using (a) Prony (b) FFT method for Iref = 1A
Figures 9.9(a) and 9.9(b) show that the two Ak corresponding to fk = 40kHz and fk = 80kHz
are much smaller than that corresponding to the fundamental frequency and its integral multiples. For the cases Iref = 1.8A and Iref = 4A corresponding to period-2 and chaotic modes,
respectively, similar results can be obtained.
Figures 9.10(a), 9.10(b), and 9.10(c) show the errors between the real signals and the reconstructed ones in the three respective cases considered here.
The simulation results of the spectral estimation using the Prony method are illustrated in
Figures 9.9(a), 9.11(a), and 9.12(a). For comparison, a similar simulation using the FFT
method was also carried out and its results are shown in Figures 9.9(b), 9.11(b), and 9.12(b).
It is obvious that the Prony method can much more accurately locate the frequencies of the
harmonics corresponding to peaks for all cases.
92
9 Chaotic Spectra Analysis Using the Prony Method
(a)
(b)
(c)
(a)
n
Ho
ng
Li
Figure 9.10: Error signals obtained with Prony method for (a) Iref = 1A (b) Iref = 1.8A and
(c) Iref = 4A
(b)
tio
Figure 9.11: PSD obtained by using (a) Prony (b) FFT method for Iref = 1.8A
Di
ss
er
ta
Figure 9.12(a) shows that there exist two inner-harmonics, 5kHz and 17kHz, corresponding
to two peaks of the PSD, which are not made visible by the FFT method (see Figure 9.12(b)).
Therefore, for chaotic signals, the Prony method is more accurate and effective than FFT.
(a)
(b)
Figure 9.12: PSD obtained by using (a) Prony (b) FFT method for Iref = 4A
9.5
Summary
This chapter put effort into finding a more accurate algorithm to calculate the spectra of chaotic
signals. Simulation results reveal that the proposed Prony method is more effective than the
conventional FFT method in estimating chaotic spectra accurately.
10 Conclusion
93
Chapter 10
Li
Conclusion
ng
This dissertation has contributed to the application of chaos control in DC-DC converters to the
end of reducing EMI, but also to system design, dynamics analysis, simulation, and hardware
implementation of chaos-controlled DC-DC converters. In particular, the contributions of the
dissertation are the following.
tio
n
Ho
1. The rapid development and application of electronic devices and products have caused
serious EMI problem. The EMI standards and the international EMC standards required
to be satisfied by converters have been introduced. After surveying the conventional
EMI suppression techniques for DC-DC converters, it has been pointed out that a new
theory, i.e., chaos theory, has great potential to provide a new means for coping with EMI
problems.
er
ta
2. The periodic and chaotic behaviour of DC-DC converters under different parametric conditions has experimentally been exhibited. Since chaos control has been proposed to
improve EMC of DC-DC converters for several decades, the conventional chaos control
methods and their advantages and disadvantages have been discussed. Some examples of
chaos control in DC-DC converters have been considered to verify their good performance
in reducing EMI.
Di
ss
3. Based on the conventional chaos control methods, a novel chaotic peak current mode
boost converter has been proposed. By the use of upper and lower reference currents,
the chaos control proposed can adjust the magnitudes of the output ripples easily, as
well as reduce EMI. A chaotic mapping corresponding to this boost converter has also
been derived, showing more complex bifurcation and chaotic phenomena. It has also been
noticed that the introduction of Ilow can facilitate bifurcation and drive the system into
chaotic mode more easily. The novel chaos control has been verified both by simulations
and experiments with simple circuitry design. It has been confirmed that not only EMI
can be suppressed, but that also the output ripples can be duly reduced by the control of
the reference current Ilow as compared with [25]. From both simulation and experimental
results, a shift of the dominant frequencies has been observed in the power spectrum when
Ilow is increased. Some further studies will be carried out in the future, so as to identify
the factors influencing the energy distribution in the chaotic power converter proposed.
4. A method for CPWM control by varying carrier frequencies or varying carrier amplitudes
has been proposed. It can distribute spectra continuously and evenly over wide frequency
ranges, thus improving the EMC of DC-DC converters. In addition, the average switching frequencies and switching dissipation of DC-DC converters are accordingly reduced,
and stability is enhanced. Analyses of the output waves and EMI properties of DC-DC
94
10 Conclusion
converters under CPWM control have been carried out. This approach provides a good
example of applying chaos control in engineering practice.
5. For implementing CPWM in practice, a novel analogue chaotic carrier has been proposed and applied in a boost converter. To generate the analogue chaotic carrier, chaotic
oscillator circuits have been introduced. The generation of analogue chaotic carriers is
simpler and cheaper than of digital ones. The simulation and experimental results show
that CPWM control with analogue chaotic carriers can greatly suppress EMI of boost
converters while the other characteristics of operation performance are well maintained.
Ho
ng
Li
6. A novel approach combining the technique of soft switching and chaos control has been
proposed for EMI reduction. Further, the digital design of chaotic carriers has been
addressed, too. Chaotic soft switching PWM has been applied in a boost converter, and
the results obtained show that EMI and efficiency of the boost converter can be improved
by chaotic soft switching PWM as compared with hard switching PWM and conventional
soft switching PWM control. This chaotic soft switching PWM control can easily be used
in different kinds of DC-DC converters. In the future, a hardware implementation and
experimental verifications will be carried further.
er
ta
tio
n
7. A one-dimensional chaotic mapping for DC-DC converters has been derived, and use of the
eigenvector method from probability theory has been proposed to calculate the invariant
density of the chaotic mapping, since chaos has random-like characteristic. Further, the
invariant density has been used to calculate the PSD and the average switching frequency
of a DC-DC converter. When a DC-DC converter works in a chaotic mode, its average
switching frequency is lower than when it works in a periodic mode. Consequently, the
switching loss of the DC-DC converter can be reduced. Moreover, the invariant density
can be used to accurately design the parameters of DC-DC converters. Simulation results
have illustrated the effectiveness of the eigenvector method.
Di
ss
8. The mean values of state variables and the size of the ripples in the input current of a
CPWM controlled DC-DC converter have been estimated. Comparing these estimation
results with ones obtained by circuit simulation, it has been found that the estimation
methods proposed are very accurate. Finally, stability, not only for the steady state but
also the dynamic state, has been proven based on the state space averaging method.
According to the above mentioned analysis, it can be concluded that CPWM control can
be applied in practice, since it is effective in suppressing EMI, stable, and causes a little
ripple increment, only.
9. The Prony method has been employed for spectral estimation of the inputs (or outputs)
of chaotic DC-DC converters. As compared with FFT, the Prony method has shown its
merits, such as improving the frequency resolution and accuracy in locating harmonics.
Thus, for analysing chaotic signals it is a better tool. In addition, the frequencies, phases,
amplitudes, and damping factors of the harmonics of currents or voltages of DC-DC
converters can also be obtained with the Prony method. The Prony method can also
distinguish between the DC and AC components of a signal. Therefore, it is recommended
to employ the Prony method of the popular FFT in such applications as the spectral
analysis of converters involving chaotic signals.
Although great effort has been practically and theoretically made in this dissertation to make
chaos control more suitable for practical applications, there are still some issues to be further
addressed in the future.
10 Conclusion
95
1. The theoretical analysis of chaotic DC-DC converters is still not self-contained, although
some analyses have been given in Chapters 7 – 9. Further issues, such as lifetime analysis
of the components in chaotic DC-DC converters, or the factors influencing the background
spectrum, are worth being investigated.
2. For CPWM control, the control circuits are to be further integrated. New application
fields for chaos control in power electronics should be explored.
Li
3. In this dissertation, chaos control has been combined with peak current mode control,
PWM control, and soft switching PWM control. Similarly, chaos control could be combined with other control schemes, such as PID or sliding mode control, to realise more
functions desirable for certain purposes.
ng
4. Chaos control should be tested in real products, such as adaptors of laptop computers or
mobile charger, to further prove the good characteristic of suppressing EMI.
Di
ss
er
ta
tio
n
Ho
5. The toolbox for spectral estimation toolbox of chaotic signals will continuously be developed and improved.
96
References
References
Li
[1] A. A. Amini and J. Nazarzadeh. Improvement behavior and chaos control of buck converter
in current mode control. Proc. IEEE Int. Conf. Industrial Technology, pp. 1 – 6, 2008.
ng
[2] M. Bagewadi, B. Fernandes, and R. Subrahmanyam. A novel soft switched boost converter
using a single switch. Proc. Power Electronics and Motion Control Conf., Vol. 1, pp. 412
– 416, 2000.
Ho
[3] M. Balestra, M. Lazzarini, G. Setti, and R. Rovatti. Experimental performance evaluation
of a low-EMI chaos-based current-programmed DC-DC boost converter. Proc. IEEE Int.
Symp. Circuits and Systems, Vol. 2, pp. 1489 – 1492, 2005.
n
[4] S. Banerjee, D. Kastha, and S. SenGupta. Minimizing EMI problems with chaos. Proc.
Int. Conf. Electromagnetic Interference and Compatibility, pp. 162 – 167, 2002.
tio
[5] A. L. Baranovski, H. Gueldner, W. Schwarz, J. Weber, and O. Woywode. On the trade-off
of ripple and spectral properties of chaotic DC-DC converters. Proc. Int. Symp. Nonlinear
Theory and Its Applications, 2002.
er
ta
[6] A. L. Baranovski, A. Mogel, W. Schwarz, and O. Woywode. Chaotic control of a DC-DC
converter. Proc. IEEE Int. Symp. Circuits and Systems, pp. II/108–II/111, 2000.
ss
[7] A. Bellini, G. Franceschini, R. Rovatti, G. Setti, and C. Tassoni. Generation of low-EMI
PWM patterns for induction motor drives with chaotic maps. Proc. 27th Annual Conf.
IEEE Industrial Electronics Society, Vol. 2, pp. 1527 – 1532, 2001.
Di
[8] E. Bilotta, P. Pantano, and F. Stranges. A gallery of Chua attractors: Part I. Int. J.
Bifurcation and Chaos, 17: 1 – 60, 2007.
[9] A. Boukabou and A. Belmahboul. Anticontrol of nonlinear dynamical systems. Proc. Int.
Conf. Information and Communication Technologies: From Theory to Applications, pp. 1
– 4, 2008.
[10] B. Bryant and M. K. Kazimierczuk. Voltage loop of boost PWM DC-DC converters with
peak current-mode control. IEEE Trans. Circuits and Systems–I, 53 (1): 99 – 105, 2006.
[11] M. C. Caponet, F. Profumo, and A. Tenconi. EMI filters design for power electronics. Proc.
IEEE 33rd Annual Power Electronics Specialists Conf., pp. 2027 – 2032, 2002.
[12] C. L. Chang and B. Hsunling. Experimental study on the performance of a single discharge
wire-plate electrostatic precipitator with back corona. Journal of Aerosol Science, 30 (3):
325 – 340, 1999.
[13] Chaos & Fractals. http://www.pha.jhu.edu/ ldb/seminar/butterfly.html, 2008.
References
97
[14] G. Chen. Controlling Chua’s global unfolding circuit family. IEEE Trans. Circuits and
Systems–I, 40: 829 – 832, 1993.
[15] K. Chen and T. A. Stuart. Soft switch-avalanche IGBT convertor. Electron. Lett., 26 (19):
1623 – 1625, 1990.
[16] X. W. Chen, W. N. Zhang, and W. D. Zhang. Chaotic and subharmonic oscillations of a
nonlinear power system. IEEE Trans. Circuits and Systems–II, 52 (12): 811 – 815, 2005.
[17] L. O. Chua, M. Komuro, and T. Matsumoto. The double scroll familly. Part I: Rigorous
proof of chaos. IEEE Trans. Circuits and Systems, 33: 1072 – 1096, 1986.
Li
[18] L. O. Chua. http://www.scholarpedia.org/article/Chua circuit, 2007.
ng
[19] H. Chung, S. Y. R. Hui, and K. K. Tse. Reduction of EMI emission from power converters using soft-switching technique. Proc. Int. Conf. Power Electronics and Variable Speed
Drives, pp. 156 – 161, 1996.
Ho
[20] H. Chung, S. Y. R. Hui, and K. K. Tse. Reduction of EMI emission from power converter
using soft-switching techniques. Electron. Lett., 32 (11): 977 – 979, 1996.
n
[21] H. Chung, S. Y. R. Hui, and K. K. Tse. Reduction of power converter EMI emission using
soft-switching technique. IEEE Trans. Electromagnetic Compatibility, 40 (3): 282 – 287,
1998.
tio
[22] P. C. Costa, A. S. Carvalho, M. F. Chouzal, and C. A. Martins. Direct torque controlfrequency analysis. Advanced Motion Control, 29: 21 – 23, 1998.
er
ta
[23] W. Cui, K. T. Chau, Z. Wang, and J. Z. Jiang. Application of chaotic modulation to AC
motors for harmonics suppression. Proc. IEEE Int. Conf. Industrial Technology, pp. 2343
– 2347, 2006.
ss
[24] X. C. Dai, J. G. Zhang, and P. X. Xu. Calculation of invariant probability distribution for
chaotic maps using eigenvector method. Journal of Applied Sciences, 4 (17): 417 – 418,
1999.
Di
[25] J. H. B. Deane, P. Ashwin, D. C. Hamill, and D. J. Jefferies. Calculation of the periodic
spectral components in a chaotic DC-DC converter. IEEE Trans. Circuits and Systems–I,
46 (11): 1313 – 1319, 1999.
[26] J. H. B. Deane and D. C. Hamill. Instability, subharmonics and chaos in power electronic
systems. IEEE Trans. Power Electronics, 5: 260 – 268, 1990.
[27] J. H. B. Deane and D. C. Hamill. Improvement of power supply EMC by chaos. Electron.
Lett., 32 (12): 1045, 1996.
[28] M. Debbat, A. El Aroudi, R. Giral, and L. Martinez-Salamero. Hopf bifurcation in PWM
controlled asymmetrical interleaved dual boost DC-DC converter. Proc. IEEE Int. Conf.
Industrial Technology, Vol. 2, pp. 860 – 865, 2003.
[29] R. C. Dixon. Spread Spectrum Systems. New York: IEEE Press, 1976.
[30] J. P. Eckmann and D. Ruelle. Ergodic theory of chaos and strange attractors. Rev. Modern
Phys., 57 (3): 617 – 656, 1985.
98
References
[31] A. S. Elwakil and M. P. Kennedy. Chua’s circuit decomposition: A systematic design
approach for chaotic oscillators. Journal of the Franklin Institute, 337: 251–265, 2000.
[32] A. Grial, A. EI Aroudi, L. Martinez-Salamero, R. Leyva, and J. Maixe. Current control
technique for improving EMC in power converters. Electron. Lett., 37 (5): 274 – 275, 2001.
[33] D. C. Hamill, J. H. B. Deane, and P. J. Aston. Some applications of chaos in power
converters.Proc. IEE Colloquium New Power Electronic Techniques (Digest No. 1997/091),
pp. 5/1 – 5/5, 1997.
Li
[34] D. C. Hamill and D. J. Jefferies. Subharmonics and chaos in a controlled switched-mode
power converter. IEEE Trans. Circuits and Systems, 35 (8): 1059 – 1061, 1998.
ng
[35] B. L. Hao. Starting from Parabola. Shanghai: Science and Technology Publishing Company,
1992.
[36] B. L. Hao. Chaotic Dynamics from Parabolic Curve. Shanghai Science and Technology
Educational Press, 1993.
Ho
[37] S. Y. R. Hui, S. Sathiakumar, and Y. Shrivastava. Progressive change of chaotic PWM
patterns in DC-AC random PWM schemes using weighted switching decision. Proc. Power
Electronics Specialists Conf., Vol. 2, pp. 1454 – 1461, 1997.
n
[38] S. H. Isabelle. A Signal Processing Framework for the Analysis and Application of Chaotic
Systems. PhD dissertation, Inst. Technol., Cambridge, MA, 1995.
er
ta
tio
[39] I. Kamwa, R. Grondin, and D. McNabb. On-line tracking of changing harmonics in stressed
power systems: Application to Hydro-Quebec network. IEEE Trans. Power Delivery, 11
(4): 2020 – 2027, 1996.
[40] M. Kuisma. Variable frequency switching in power supply EMI-control: An overview. IEEE
AES Systems Magazine, 18 (12): 18 – 22, 2003.
ss
[41] A. Lasota and M. Mackey. Chaos, Fractals and Noise: Stochastic Aspects of Dynamics,
Vol. 9. Applied Mathematical Sciences Series. New York: Springer-Verlag, 1994.
Di
[42] J. H. Lee and H. T. Kim. Selecting sampling interval of transient response for the improved
Prony method. IEEE Trans. Antennas and Propagation, 50 (1): 74 – 76, 2003.
[43] Z. Leonowicz, T. Lobos, and J. Rezmer. Advanced spectrum estimation methods for signal
analysis in power electronics. IEEE Trans. Industrial Electronics, 50 (3): 514 – 519, 2003.
[44] H. Li, Z. Li, W. A. Halang, and B. Zhang. Controlling DC-DC converter with chaos-based
PWM. Proc. 5th EUROMECH Nonlinear Dynamics Conf., pp. 1207 – 1211, 2005.
[45] H. Li, Z. Li, K. S. Tang, and W. A. Halang. A chaotic soft-switching PWM boost converter
for EMI reduction. Proc. IEEE Int. Symp. Industrial Electronics, pp. 341 – 346, 2008.
[46] H. Li and B. Zhang. Calculation of invariant probability density distribution for chaotic
map in DC-DC converter and its application. Proc. Chinese Society for Electrical Engineering, 23 (25): 54 – 60, 2005.
[47] T. Lobos, Z. Leonowicz, and J. Rezmer. Harmonics and interharmonics estimation using
advanced signal processing methods. Proc. 9th IEEE Int. Conf. Harmonics and Quality of
Power, Vol. I, pp. 335 – 340, 2000.
References
99
[48] T. Lobos, J. Rezmer, and H. J. Koglin. Analysis of power system transients using wavelets
and prony methods. Proc. IEEE Porto Power Tech Conf., pp. 10 – 13, 2001.
[49] T. Lobos, J. Rezmer, and P. Schegner. Parameter estimation of distorted signal using
prony method. Proc. IEEE Bologna Power Tech Conf., pp. 23 – 26, 2003.
[50] Y. Lu, X. Huang, B. Zhang, and Z. Mao. Two chaos-based PWM strategies for suppression
of harmonics. Proc. 6th World Congress Intelligent Control and Automation, Vol. 1, pp.
953 – 957, 2006.
Li
[51] J. Mahdavi, A. Emaadi, M. D. Bellar, and M. Ehsani. Analysis of power electronic converters using the generalized state-space averaging approach. IEEE Trans. Circuits and
Systems–I, 44 (8): 767 – 770, 1997.
ng
[52] S. Maity, D. Tripathy, T. K. Bhattacharya, and S. Banerjee. Bifurcation analysis of PWM1 voltage-mode-controlled buck converter using the exact discrete model. IEEE Trans.
Circuits and Systems–I, 54 (5): 1120 – 1130, 2007.
Ho
[53] S. L. Marple. Digital Spectral Analysis with Applications. Englewood Cliffs, NJ: Prentice
Hall, 1987.
n
[54] S. L. Marple. A tutorial overview of modern spectral estimation. Proc. IEEE Int. Conf.
Acoustics, Speech, and Signal Processing, Vol. 4, pp. 2152 – 2157, 1989.
tio
[55] R. Martin. Noise power spectral density estimation based on optimal smoothing and minimum statistics. IEEE Trans. Speech and Audio Processing, 9: 504 – 512, 2001.
er
ta
[56] M. F. McGranaghan, R. M. Zavadil, and G. Hensley. Impact of utility switched capacitors
on customer systems-magnification at low voltage capacitors. IEEE Trans. Power Delivery,
7 (2): 862 – 868, 1992.
ss
[57] R. Mukherjee, S. Nandi, and S. Banerjee. Reduction in spectral peaks of DC-DC converters
using chaos-modulated clock. Proc. IEEE Int. Symp. Circuits and Systems, Vol. 4, pp. 3367
– 3370, 2005.
Di
[58] E. Ott, C. Grebogi, and J. A. Yorke. Controlling chaos. Physical Review Letters, 64: 1196
– 1199, 1990.
[59] G. Poddar, K. Chakrabarty, and S. Banerjee. Control of chaos in DC-DC converters. IEEE
Trans. Circuits and Systems–I, 45: 672 – 676, 1998.
[60] A. Rényi. Representation for real numbers and their ergodic properties. Acta Math. Acad.
Sci. Hung., 8: 477 – 493, 1957.
[61] C. Rohrs, J. Melsa, and D. G. Schultz. Linear Control Systems. Electronic Technical Publishing Services, 1993.
[62] P. S. Ruggera and E. R. O’Bryan. Studies of apnea monitor radio frequency electromagnetic
interference. Proc. 13th Annual Int. Conf. IEEE Engineering in Medicine and Biology
Society, Vol. 13, pp. 1641 – 1643, 1991.
[63] V. M. M. Saiz and J. B. Guadalupe. Application of Kalman filtering for continuous realtime tracking of power system harmonics. IEE Proc. Generation, Transmission and Distribution, 144 (1): 13 – 20, 1997.
100
References
[64] E. Sakai, K. Harada, G. Ariyoshi, and K. Yamasaki. Stability analysis of boost converters
using electric double-layer capacitors as output filter. Proc. 29th IEEE Power Electronics
Specialists Conf., Vol. 1, pp. 367 – 373, 1998.
[65] J. Shao, R. L. Lin, F. C. Lee, and D. Y. Chen. Characterization of EMI performance for
hard and soft-switched inverters. Proc. Applied Power Electronics Conf. and Exposition,
Vol. 2, pp. 1009 – 1014, 2000.
[66] M. M. Tawfic and M. M. Morcos. ANN-based techniques for estimating fault location on
transmission lines using Prony method. IEEE Power Engineering Review, 16 (2): 219 –
224, 2001.
Li
[67] S. J. Underwood. DC-DC converters suppress EMI: Minimizing EMI at its source.
http://powerelectronics.com/mag/power dcdc converters suppress/, 2002.
ng
[68] Y. Wang and N. H. Wang. Study of analyzing electrostatic precipitator discharge signal
based on the Prony method. The Proc. of CSEE, 23 (1): 141 – 144, 2003.
Ho
[69] Z. Wang and K. T. Chau. Design and analysis of a chaotic PWM inverter for electric
vehicles. Proc. Industry Applications Conf., pp. 1954 – 1961, 2007.
n
[70] Z. Wang, K. T. Chau, and C. Liu. Improvement of electromagnetic compatibility of motor
drives using chaotic PWM. IEEE Trans. Magnetics, 43 (6): 2612 – 2614, 2007.
tio
[71] J. Weber, O. Woywode, H. Guldner, A. L. Baranovski, and W. Schwarz. New method
for tailoring ripple and spectral properties of chaotic DC-DC converters. Proc. IEEE Int.
Symposium Circuits and Systems, Vol. 4, pp. IV-556 – IV-559, 2002.
er
ta
[72] C. Wei, K. T. Chau, Z. Wang, and J. Z. Jiang. Application of chaotic modulation to AC
motors for harmonic suppression. Proc. IEEE Int. Conf. Industrial Technology, pp. 2343
– 2347, 2006.
ss
[73] D. M. Witters and P. S. Ruggera. Electromagnetic compatibility (EMC) of powered wheelchairs and scooters. Proc. Rehabilitation Society of North America, pp. 359 – 360, 1994.
Di
[74] J. R. Wood. Chaos: A real phenomenon in power electronics. Proc. IEEE Applied Power
Electronics Conf. Rec., pp. 115 – 124, 1989.
[75] R. Yang, B. Zhang, F. Li, and J. J. Jiang. Experiment research of chaotic PWM suppressing
EMI in converter. Proc. IEEE 5th Int. Conf. Power Electronics and Motion Control, Vol. 1,
pp. 1 – 5, 2006.
[76] R. Yang, B. Zhang, and Y. P. Zhang. A novel chaotification control scheme in DC-DC
converter. Proc. Applied Power Electronics Conf., pp. 1489 – 1494, 2007.