* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download INFS 795 PROJECT: Custering Time Series
Survey
Document related concepts
Transcript
INFS 795 PROJECT:
Clustering
Time Series
presented by
Rafal Ladysz
AGENDA
• INTRODUCTION
– theoretical background
– project objectives
– other works
• EXPERIMENTAL SETUP
– data description
– data preprocessing
– tools and procedures
• RESULTS AND CONCLUSIONS (so far)
• NEXT STEPS
• REFERENCES
INTRODUCTION: theoretical background
• clustering: unsupervised ML technique of grouping similar,
unlabeled objects without prior knowledge about them
• clustering techniques can be divided and compared in many
ways, e.g.:
–
–
–
–
exclusive vs. overlapping
deterministic vs. probabilistic
incremental vs. batch learning
hierarchical vs. flat
or:
–
–
–
–
partitioning (e.g. k-means, EM)
hierarchical (agglomerative, divisive)
density-based
model-based: a model is hypothesized for each of the clusters to find
the best fit of that model to each other
INTRODUCTION : theoretical background
•
example of partitioning algorithms:
– k-means
– EM: probabilistic generalization of k-means
•
k-means characteristics:
– suboptimal (susceptible to local minima)
– sensitive to initial conditions and... outliers
– requires number of clusters (k) as part of the input
– Euclidean distance is its most natural dissimilarity metrics (spherical)
– we remember how it works: re-partitioning until no changes
•
EM characteristics:
– generalization of k-means to probabilistic setting (maintains probability of
membership of all clusters rather than assign elements to initial clusters)
– works iteratively:
• initialize means and covariance matrix
• while the convergence criteria is not met compute the probability of
each data belonging to each cluster
• recompute the cluster distributions using the current membership
probabilities
– cluster probabilities are stored as instance weights using means and standard
deviations of the attributes
– procedure stops when likelihood saturates
INTRODUCTION: theoretical background
• distance / (dis)similarity measures
– Euclidean: root square of sum of squares
– main limitation: very sensitive to outliers!
• Keogh claims that
– Euclidean distance error rate: about 30%
– DTW error rate: 3%
• but there is cost for accuracy:
– time to classify an instance using Euclidean distance 1 sec
– time to classify an instance using DTW 4,320 sec
• by the way: DTW stands for Dynamic Time Warping
(illustration and formula follow)
INTRODUCTION: project objectives
• in general: clustering of “evolving” time series data
– issues to be taken into consideration:
• dimensionality
• outliers
• similarity measure(s)
• number of elements (subsequences)
• overall evaluation measure(s)
– context: recognition-based support for another algorithm
• in particular: comparing and/or evaluating
– efficiency and accuracy of k-means and EM
– effect of initial cluster position for k-means accuracy
– efficiency* and accuracy** of Euclidean and DTW distance
measures in initializing cluster seeds for k-means
INTRODUCTION: other works
• E. Keogh et al.: inspired to use DTW as
alternative for Euclidean (DTW origins from
experiments in 1970s with voice recognition)
• D. Barbara: outlined prerequisites for clustering
data streams
• H. Wanng et al.: described techniques used in
detecting pattern similarity
– similarity is “buried” deeply in subspaces; not direct
relevance to my experiments since arbitrarily
selected attributes (time series require temporal
order)
PROJECT OBJECTIVES: summary
• challenges
– data: evolving time series (?!)
– k-means: initialization of seeds position and k
(attempt of automatic optimization for the evolving data)
– similarity measure: Euclidean - error-prone, DTW - costly
– real time requirement (as target solution, not in the project)
– tools: necessity to create (some of them) from scratch
– not encountered in the literature
• motivation
– support for already designed and implemented software
– comparing k-means vs. EM and Euclidean vs. DTW
– the challenges listed above
EXPERIMENTAL DESIGN: data description
• three sources of data for more general results
– medical: EEG* and EKG* http:
– financial: NYSE* and currency exchange http:
– climatological: temperature and SOI* http:
• all the data are temporal (time series), generated in
their natural (not simulated) environments
• some knowledge available (for experimentator, not
the machine)
• brief characteristics:
EXPERIMENTAL DESIGN: data description
heart
failure
occurrences
epileptic
seizure
duration
examples of medical data: heart-related EKG (top) and brain-related EEG (bottom)
EXPERIMENTAL DESIGN: data description
seasonality
(annual cycle)
periodicity
or chaos?
examples of medical data:
temperature in Virginia (top)
Southern Oscillation Index
(bottom)
EXPERIMENTAL DESIGN: data description
do we see any patterns
in either of these two?
examples of financial data:
New York Stock Exchange (top)
and currency exchange rate (bottom)
notice: both time series
originates from “cultural”
rather than “natural”
environment
Dynamic Time Warping
Euclidean
one-to-one
(i-1, j)
(i, j)
Dynamic Time Warping
many-to-many
(i-1, j-1)
(i, j ) d (qi , c j ) min{ (i 1, j 1), (i 1, j ), (i, j 1)}
(i, j-1)
where γ(i, j) is the cumulative distance of the
distance d(i, j) and its minimum
cumulative distance among the adjacent cells
EXPERIMENTAL DESIGN: data preprocessing
• normalization: not necessary*
• outliers detection: not done for the exper. data
sets
remark: not feasible for real-time scenario (assumed)
• subsequencing: using another program (LET*)
for Euclidean distance measure: equal length required –
done
• computing mean for each subsequence and
value shifting
to enable Euclidean metrics capture
similarity of s.s. – done
• applying weighs to each
“dimension” (discrete sample value)
to favorize dimensions (points) closer
to cut-off (beginning) of the s.s.
EXPERIMENTAL DESIGN: big picture
• the general experimental proceeding regarding
initialization:
FOR all (six) time series data
FOR dimensionalities D = 30, 100
FOR subsequence weights w(1)*, w(1.05)*
FOR = 5%, 10%
FOR both (E, DTW) distance measures
FOR both constraints (Kmax, Ŝ)
– capture and remember cluster seeds
– apply to “real” clustering
6x2x2x2x2x2 = 192 seed sets
– evaluate final goodness
EXPERIMENTAL DESIGN: initialization
• initialization phase: collecting cluster seeds
subsequences in D-dimensional space
• computing distance between the subsequences using
Euclidean (E) and DTW (D) measures using matrices
• compare pair wise distances from matrices E and D
• based on the above, create initial cluster seeds
• see next slide (SPSS)
EXPERIMENTAL DESIGN:
tools and procedures
• the core for the experiment is generating initial k
cluster seeds (to be further used by k-means)
• that is done using 2 distance measures: E. and DTW
• once the k seeds are generated (either way), their
positions are remembered and:
– each seed is assigned a class for final evaluation
– the initial cluster positions and/or classes are passed on
to the clustering program (SPSS and/or Weka)
• effective that moment, the algorithms are working
unattended
• the objective is to evaluate impact of initial clusters
optimization (in terms of their positions and number)
EXPERIMENTAL DESIGN:
tools and procedures
• initial cluster seeds – algorithmic approach
– define constraints: Kmin, Kmax, k = 0, , S, Ŝ
– start capturing time series subsequences (s.s.)
– assign first seed to first s.s., increment k
– do while either condition is fulfilled:
k = Kmax OR S = Ŝ OR no more subsequences
if new s.s. is farther than from any seeds,
create new seed assigned to that s.s., increment k
otherwise merge the s.s. to existing seed not farther than
compute S
• stop capturing s.s., label all generated seeds
EXPERIMENTAL DESIGN:
tools and procedures
• how the number of clusters (seeds) is
computed?
• as we know, a “good” k-means algorithm
minimizes intra- while maximizing interdistances (thus grouping similar objects in
separate clusters, not too many, not too few)
• the objective function used in the project is
S = <intracl. dist.>/<intercl. dist.>
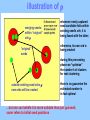
illustration of S
S = <intra>/<inter>
Kmin
k: number of clusters
this plot shows the idea of when to stop capturing new cluster seeds;
the measure is the slope between two neigboring points
to avoid “too early” termination, constrain of Kmin should be imposed
illustration of
merging seeds:
within “original”
orb
“original”
seeds
whenever newly captured
seed candidate falls within
existing seed’s orb, it is
being fused with the latter;
otherwise, its own orb is
being created
during this processing
phase we “optimize”
the number k of clusters
for real clustering
outside existing seed orbs :
new orbs will be created
there is no guarantee the
estimated number is
in fact optimal
...but one can beliefe it is more suitable than just guessed;
same refers to initial seed positions
EXPERIMENTAL DESIGN:
tools and procedures
• computing Euclidean and DWT distances:
– coding my own program;
– temporarily: using a program downloaded from Internet
time series
subsequences
computing distances
(Euclidean and DTW)
k-means, EM
(SPSS)
• evaluating influence of initialization on clustering accuracy:
SPSS for Windows, ver. 11 (Standard Edition)*
• comparing performance (accuracy and runtime) of k-means
and EM: Weka
RESULTS AND CONCLUSIONS (so far)
• after running 12 k-means sessions over 6
preprocessed datasets,
• the average improvement WITH
INITIALIZATION over WITHOUT can be
approximated as
39.4/112 vs. 77/110, i.e.
0.35 vs. 0.7
• “improvement” is computed as the ratio of
intra/inter
summarizing: RESULTS to be reported
• performance measure of k-means WITH and
WITHOUT initialization
– goodness evaluation (S)
– subjective evaluation of clustering
• performance comparison of k-means and EM
in same circumstances
• performance comparison of Eucl. and DTW
– error
– runtime
NEXT STEPS
• since now to project deadline
– finishing E/DTW distance computing program
– finishing k-optimizing program
– generating 192 initial cluster seeds
– clustering using the above initial cluster seeds
– comparing with no initialization
• after deadline (continuation if time allows)
– write own k-means program (to run the whole
process in one batch, thus truly measuring
performance)
– if results promising, embedding into another
program (LET*)
REFERENCES
Wang, H. et al.: Clustering by Pattern Similarity in Large Data Sets
Perng, C-S. et al.: Landmarks: A New Model for Similarity-Based Pattern...
Aggarwal, C. et al.: A Framework for Clustering Evolving Data Streams
Barbara, D.: Requirements for Clustering Data Streams
Keogh, E., Shruti, K.: On the Need for Time Series Data Mining...
Gunopulas, D., Das, G.: Finding Similar Time Series
Keogh, E. et al.: Clustering of Time Series Subsequences is Meaningless...
Lin, J. et al.: Iterative Incremental Clustering of Time Series
Keogh, E., Pazzani, J.: An enhanced representation of rime series...
Kahveci, T. et al.: Similarity Searching for Multi-attribute Sequences
and other information and public software resources found over Internet.