Download Internal Resistance of a Battery Activity

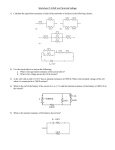
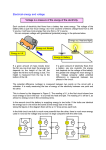
Internal Resistance of a Battery Lab
Name:
Period:
AP Physics
One of the interesting ideas that might occur to you in thinking about circuits is that if a battery were hooked up to a
conductor with zero resistance, there would be no limit on the amount of current flowing through the resistor:
V 9V
I= =
= ∞ A.
R 0
There are such things as conductors with no resistance – they are called superconductors – however they never end up with
unlimited amounts of current flowing through them. This is because every voltage supply – even a battery – has some
resistance inside of it – we call it the internal resistance – and this limits how much current that battery can supply.
An interesting effect of the internal resistance is that it causes the charges in the current to lose some of their voltage
before they even make it out of the battery. This means the voltage supplied by the battery is actually less than it
theoretically should be. We call the theoretical voltage supplied by a battery its electromotive force (or EMF for short) and
the actual voltage that we measure at its electrodes is called its terminal voltage.
The internal resistance of a battery depends on the materials from which the battery is made and the condition it is in. As
batteries get older their internal resistance increases, which means more of the EMF is used up getting through the battery
and less it available as terminal voltage to power a circuit.
To analyze the effect of the internal resistance, we treat it like it is in series with the rest of the load – in this case a single
variable resistor – called a potentiometer or a rheostat.
The circuit we are analyzing
looks like this:
If we break the battery down
into its parts: the supplier of
EMF and the internal
resistance, r.
Put it all together and you’ve
got:
where V is the terminal voltage
of the battery and R is the
variable resistor in the load.
Circuit Analysis:
1. Find an expression (using variables) for the
total resistance of the circuit:
2. Use Ohm’s Law (Vtotal=IRtotal) and find an
expression relating the EMF, measured current
and total resistance:
3. Solve your expression for IR:
4. Realizing that the terminal voltage, V is equal
to IR (this is ohm’s law as we’ve been using it all
along) find an expression for terminal voltage as a
function of EMF, I and r:
Procedure:
1. Connect voltmeter and ammeter to circuit as
shown in this diagram:
2. Measure the terminal voltage of the battery on the voltmeter and the current through the circuit on the
ammeter at a variety of settings for R. You will not measure R, simply adjust it and read off the
terminal voltage and the current.
Terminal Voltage (V)
Current (I)
3. Graph your results (terminal voltage on the y-axis and current on the x-axis) and find the equation for
your line of best fit.
4. Based on the equation you derived in step 4 of the circuit analysis and your graph determine the EMF
of the battery and its internal resistance, r. (How does your theortetical equation correspond to the best
fit equation for graph?),
EMF =
r=