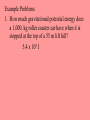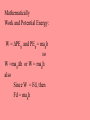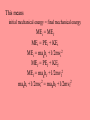* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download Chapter 8 PowerPoint
Survey
Document related concepts
Transcript
Chapter 8 Work, Energy, and Power Chapter Warm Up 1. What is a non-science meaning of the term “work”? Give an example. 2. What is the scientific meaning of the term “work”? Give an example. 3. What is a non-science meaning of the term “energy”? Give an example. 4. What is the scientific meaning of the term “energy”? Give an example. 5. What are two different types of energy? 6. What is the Law of Conservation of Energy? Section 1: Work Definition: The product of the force on an object and the distance through which the object is moved. Work is done when a force moves an object through a distance. Work is done by the force on the object. The force and direction must be parallel. Symbol: W Units: kgm2/s2= Joule (J) Equation: W Force; W distance (d) W Fd; if force in kgm/s2 and distance in m, Then W=Fd Not a vector quantity(it’s something called a dot product) 1J = work done lifting 1 kg a height of 1 meter. Example Problems 1. A tugboat pulls a ship with a constant horizontal force of 5.00 x 103 N across a harbor. How much work is done on the ship if it moves 3.00 km? 1.50 x 107 J 2. What net force is required to do 2.55 x 103 J of work on a crate to move it 5.00 m? 5.10 x 102 N 3. How far will a car move if 4.58 x 107 J of work is done on it by a net force of 362 N? 1.27 x 105 m Section 2: Energy Definition: Capacity or ability to do work Ways to classify energy: Source: Nuclear, chemical, mechanical, magnetic, electrical, gravitational, solar, hydrodynamic, thermal, wind, geothermal Physical Form Mechanical Nonmechanical We will deal with mechanical energy only Two Types of Mechanical Energy: Potential Kinetic Potential Energy Energy of position Energy an object has due to its position in a field 3 classifications Gravitational Potential Energy Magnetic Potential Energy Electrical Potential Energy Gravitational Potential Energy Definition: The energy an object has due to its position in a gravitational field The amount of gravitational potential energy an object has is independent of the path it took to get to its position Example The amount of potential energy a hiker gains climbing a mountain. Symbol: PEg Units: kgm2/s2 (Joule) Equation: PEg mass, height, and acceleration PEg = magh use h instead of y -- convention Example Problems 1. How much gravitational potential energy does a 1,000. kg roller coaster car have when it is stopped at the top of a 55 m lift hill? 5.4 x 105 J 2. A ski lift has a vertical elevation change of 1390 m. If a skier rides to the top of the lift and gains1152 kJ of gravitational potential energy, what is the skier’s mass? 8.45 x 101 kg 3. An apple with a mass of 95.0 g is carried from the street level of a building to its roof and gains 355 J of gravitational potential energy. How tall is the building? 3.81 x 102 m Kinetic Energy Definition: The energy an object has due its motion. Example: The energy a baseball has as it is flying through the air towards home plate. Symbol: KE Units: kgm2/s2 (Joule) – it is energy after all! Equation: KE mass; KE velocity – after a lot of algebra, get KE = ½ mv2 Example Problems: 1. How much kinetic energy does an 850. kg car have if it is traveling at 35.0 m/s? 5.21 X 105 J 2. A cheetah is traveling at a speed of 31.3 m/s. If it has 3.11x 104 J of kinetic energy, what is the mass of the cheetah? 63.5 kg 3. An emperor penguin has a mass of 35 kg. The penguin has 149 J of kinetic energy. How fast is the penguin swimming? 2.9 m/s Section 3: Work and Energy How can work and energy be related? Work is the amount of PEg an object gains when moved in a gravitational field, And KE is the amount of work an object can do while changing velocity Mathematically Work and Potential Energy: W = PEg and PEg = magh so W =magh or W = magh also Since W = Fd, then Fd = magh Example Problems 1. How much work is done by a hiker on a 15.0 kg backpack that is lifted up a height of 10.0 m? 1.47 x 103 J 2. How far does a 2.50 kg book have to be raised to do 12.5 J of work on the book? 0.510 m 3. 1.25 J of work is done on a Teddy Bear by raising it 1.10 m in to the air. What is the mass of the Teddy Bear? 0.116 kg Work and Kinetic Energy: Work – Kinetic Energy Theory W = KE W = KEf - KEi W = 1/2mvf2 – 1/2mvi2 Since W= Fd; Fd = 1/2mvf2 – 1/2mvi2 Example Problems; 1. 75 kg bobsled is pushed from rest along a horizontal surface by two athletes. After the bobsled has been pushed a distance of 4.5 m, its speed is 6.0 m/s. What is the magnitude of the net force on the bobsled? 3.0 x 102 N 2. A 30.0 kg box initially sliding at 5.00 m/s on a rough surface is brought to rest by 20.0 N of friction. What distance does the box slide? 18.8m 3. A space ship of mass 5.00×104 kg is traveling at a speed 1.15 × 104 m/s in outer space. Except for the force generated by its own engine, no other force acts on the ship. As the engine exerts a constant force of 4.00 × 105 N, the ship moves a distance of 2.50 × 106 m in the direction of the force of the engine. Determine the final speed of the ship. 1.31 x 104 m/s 4. A car experiences a net force of 57.7 N while it is slowing down from 25.0 m/s to 20.0 m/s over a distance of 325m. What was the car’s mass? 1.67 x 102 kg Section 4: Conservation of Energy LAW OF CONSERVATION OF ENERGY: Energy may not be created nor destroyed, it only changes form. OR The amount of energy in a closed system is constant. Conservation of Mechanical Energy Mechanical energy is the energy an object has due to its position or motion. Mechanical energy is not always conserved – some may be converted to heat energy(friction) But, if friction is negligible, mechanical energy is conserved. This means initial mechanical energy = final mechanical energy MEi = MEf MEi = PEi + KEi MEi = maghi +1/2mvi2 MEf = PEf + KEf MEf = maghf +1/2mvf2 maghi +1/2mvi2 = maghf +1/2mvf2 Example Problems 1. Donald Duck is at the top of Mt. Gushmore, at an elevation of 28.0 meters. Donald has a mass of 52.5 kg. He goes down the waterslide to the bottom of Mt. Gushmore. How fast is Donald going when he is at the bottom of the slide? 23.4 m/s 2. A pendulum bob is released from some initial height such that the speed of the bob at the bottom of its swing is 1.9 m/s. What is the initial height of the bob? 0.18m 3. Starting from rest, a 25.0 kg child goes down a 3.00 m tall slide. How fast is she going when she is halfway down the slide? 5.42 m/s Section 5: Power Definition: The rate at which energy is transferred from one form to another. Rate at which work is done. Rate implies time Symbol: P Unit: kgm2/s3 = Watt (W) – J/s Equations Power = P = work/t If vertical motion: P = mag(hf –hi)/t If horizontal motion: P = Fd/t Example Problems: 1. A 193 kg curtain must be raised 7.5 m in no more than 5.0 seconds. How much power is needed to do this? 2.8 X 103 kgm2/s3 (W) 2. A rain cloud contains 2.66 x 107 kg of water vapor. How long would it take for a 2.00 x 103 W pump to raise the same amount of water to the cloud’s altitude, 2.00 km? 2.61 x 108 s 3. A ship generates 5.6 x 107 W of power. How much work can this ship do in 1.0 hour? 2.0 x 1011 kgm2/s2 (J)