Download Putting electrons in motion Electron movement through conductors

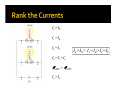
Putting electrons in motion
Electron movement through conductors
 Resistivity and Resistance – Ohm’s Law
 Electrical Power


Current is the flow rate of charges through a surface area.
 The direction of the current is the direction of the flow of positive charges.

Q
I av 
t
dQ
I (t ) 
dt
(C/s=Amperes)
Q  ( nV ) q
Q  ( nAx ) q
Q  ( nAvd t ) q
Q
I av 
 nqvd A
t
vd : Drift Velocity
A = 3.31 x 10-6 m2
I = 10 A
Cu = 8.92 g/cm3
Q
 nqvd A
I av 
t
10 A  nvd 1.6 10 19 3.3110 6

V
m = 63.5 g/mol
NA = 6.02 x 1023 at/mol
1 electron per Cu atom
m




63.5
 7.12cm3 / mol
8.92
N A 6.02 10 23

 8.46 10 22 el / cm3  8.46  10 28 el / m 3
n
V
7.12
10
4
vd 

2
.
23

10
m/s
19
6
28
1.6  10
3.31 10 8.46  10




Current Density:
I
J   nqvd
A
J  nqv d
(for a uniform current
perpendicular to the cross-section)
General vector definition
In some materials, the field applied and the current
density are proportional.
Ohm’s Law:
J  E
Most metals obey Ohm’s Law
: conductivity
V  El 
R
Metal
 l 
l   I

 A 
J
l
V

A
I
Semiconductor diode
(V/A = )
Resistivity is the inverse of conductivity.
 Both are intrinsic properties of the material.
 Resistance is a also a function of the shape and size of the device.


1

l
R
A
Material
 (.m)
Copper
1.7x10-8
Gold
2.44x10-8
Aluminum
2.82x10-8
Silicon
640
Rubber
~1013
A=2x10-4 m2
Al = 2.82x10-8 .m
10 cm
RAl   Al
Glass = 3x1010 .m
l
 2.82  10 8
A



RGlass   Glass

 0.1 
5
1
.
41
10





4
 2 10 
l
 0.1 
13

1
.
5

10

 3  1010 

4
A
 2 10 
 b
R
ln 
2L  a 
C
L
b
2ke ln 
a
Atoms
Electrons
A regular array of
atoms surrounded
by a “cloud” of free
electrons
Random
movement under
zero field
Random
movement
modified by a field
F  qE  mea
qE
a
me
J  E
qE
t
v f  v i  at  v i 
me
Now take the average over all
times. Then vi = 0 (random
movement),
v f  vd 
nq 2 E

J  nqvd 
me
qE
qE

t
me
me
, where  is the mean
time between collisions
nq 2

me
me
 2
nq 
l    vd
is the mean free path
Resistivity in metals is linear with temperature over a limited range
   0 1   T  T0 
R  R0 1   T  T0 
: temperature coefficient of resistivity
1 

 0 T
(C-1)
U battery  QV
I
U resistor (heat )  U battery
+
-
V
R
U QV

 IV
Electrical Power
t
t
V.A = Watts(W)
P  IV

V 
R
2
Symbol of a Resistor
P I
2
R
Power Dissipated
on a Resistor
Ia=Ib
Ic=Id
Ie=If
Ia=Ic+Ie
P60W > P30W
Ic>Ie
Ia=Ib> Ic=Id>Ie=If
Current is the net rate of charge flow.
Electrons move at the drift velocity.
Resistance is the ratio of voltage applied to current. The ratio is linear for most metals.
 Resistivity is a material property.
 Electrical energy will be converted to thermal energy on a resistor. The rate of conversion is the power.




Reading Assignment
 Chapter 28 – Direct Current Circuits

WebAssign: Assignment 5