Download Numerical Ages 1 -

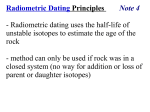
Absolute Time
Part 1 -- Radioactivity
Unless otherwise noted the artwork and photographs in this slide show are original and © by Burt Carter.
Permission is granted to use them for non-commercial, non-profit educational purposes provided that credit is given for their origin.
Permission is not granted for any commercial or for-profit use, including use at for-profit educational facilities.
Other copyrighted material is used under the fair use clause of the copyright law of the United States.
What to Look For:
• Certain configurations of atomic nuclei are inherently unstable.
We call atoms that have these configurations radioactive
isotopes.
• These atoms are subject to spontaneous “decay” which stabilizes
the structure, either in one or several steps.
• beta decay occurs when a neutron expels an electron, leaving it
(+), and therefore a proton. This raises the atomic number by 1
but doesn’t change the atomic mass. (14C to 14N)
• electron capture decay is the opposite. A proton absorbs an
electron and becomes a neutron. This lowers the atomic number
without changing the atomic mass. (14N to 14C)
• alpha decay occurs when the nucleus emits 2 protons and 2
neutrons – a helium nucleus or alpha particle. (U to Pb involves
several of these, as well as some betas).
• The half-lives of even very long-lived isotopes can be determined
by calculation from their easily determined decay constants.
When Earnest Rutherford received the Nobel
prize it was not just for working out the amount
of heat energy released by radioactive
elements. It was for working out the
mechanism of that heat release and its
consequences and implications.
Not only did that work “discover the additional
heat source” supposedly postulated by Kelvin,
it also discovered, at last, a type of natural
clock which was “wound” at the appropriate
time for determining the age of the Earth
(unlike the “Nile Delta clock” discussed earlier)
and which has not yet run down (unlike the
Ocean Salinity clock). Furthermore there are
many copies of this clock in the world, all of
them wound at different, but known, times, so
we can date many events other than the origin
of Earth. Finally, various versions of the clock
run at different rates, so we can date very old
events with some clocks almost as precisely as
we can young events with other clocks.
Ernest Lord Rutherford.
Photographer unknown.
First let’s look at the ways natural clocks work, both those that are useful and
those that are not. We will begin with linear clocks. One way people used to
keep track of short (but not tiny) periods of time was by carefully burning candles.
This system works if 1) you are not interested in very
small blocks of time, and 2) you are only interested in
fairly short blocks, or, alternately, 3) you are
careful to light a new candle at the exact
time the old one burns out, for as long
as is necessary to measure a big
block of time.
This works because candles deliver fuel
(wax) to the flame at a pretty predictable
rate. The wax (similar to oil when melted)
“wicks” up the “wick” because of its surface
tension and cohesion. Because the
properties of molten wax and candle wicks
are pretty consistent, the rate of delivery
and therefore the burn rate is fairly constant.
This is a “linear” process because if you graph the candle length against the time that it has
been burning the result is a straight line. In this diagram we have used “half-lives” as the
unit of time, for reasons that will become obvious. If the entire candle will burn for, say, two
hours, the “half-life” is one hour. Note the straight line (dotted) that describes the burn rate.
Both the accumulation of sediment on the Nile Delta and the accumulation of salt in the
ocean were assumed to be linear, and this is probably not too bad an assumption. (Until
the sediment source is worn down.) Notice that after two half-lives the candle is gone, as
the ocean was “full” of salt. The clock runs down and afterwards you can’t tell when it did.
Of course a candle can be marked
off into however many segments
you wish if you have a good ruler.
Photograph by Thomas H. Johnson, Jr.
Not all burning is linear, however. You are probably familiar with how open fires work.
Once burning, with a good load of wood, they blaze bright and hot, but if you don’t add
more wood periodically they “burn down”.
They way a fire burns down is “non-linear” because the fuel is not delivered at a steady rate to
the flame. There is, over time, less fuel available, so the fire “burns down” over time. As long
as you sit beside the fire this is obvious and you can add more wood to keep the flame the size
you like, but once you crawl into the tent the fire inevitably goes out. But the rate at which it
goes out slows, so if you’re lucky there will still be hot coals in the morning to restart it.
The graph shows the rate of wood consumption of a typical fire. early on
the fire burns the fuel rapidly, producing a lot of heat and light, but this rate
slows, predictably, and the heat/light output diminishes as a result. The red
lines point out that half the wood is consumed in far less than half the total
burn time. That is, there are more than two half-lives in the process.
It would seem that a non-linear process like an open fire might make a better clock
than a candle because you wouldn’t have to light a new one as often. However,
there are too many variables for this to be accurate. Different types of wood burn at
different rates, different sizes of wood from the same tree burn at different rates
because of differences in surface area and volume. And whereas it is easy to make
a mark half-way down a candle, it is essentially impossible to tell when exactly half
a stack of wood has burned away. Most of the product goes up in smoke, literally.
Still, if you’ve seen enough old cowboy movies you know that posse scouts use
fires as rough clocks. A good one can tell how many hours ahead the bad guys are
by how warm their fire still is. This works because oater bad guys, being bad guys,
ignore Smokey Bear and never put out their campfires. Idiots.
(Incidentally, if you don’t know that good
posse scouts can do this then you need to go
check out more cowboy movies. You’re
Americans for crying out loud (or learning
about American culture) and you should be
familiar with cowboy mythology. Be sure you
include “Shane”, some John Wayne (including
the first “True Grit”), and the spaghetti
westerns of Sergio Leone and Clint Eastwood
in your viewing list.)
The most important thing that Rutherford discovered about radioactivity (for our
purposes in this class) was that it can be used as a non-linear clock that doesn’t
have the same problems as an ordinary fire.
Unlike an unfed fire (which will last a matter of hours or days) it runs for a long
time (1000’s to over 10 billion years) in enough (but not all) cases to be useful.
In addition it is comparatively easy to tell at any point in the process how far it
has proceeded, if you have the right equipment, because all of the residue
ordinarily remains and can be measured along with the unconsumed “fuel”. If this
is not the case, it will be obvious.
First we will look at the process and a bit of how Rutherford worked out its
characteristics, then we’ll look at the machine and what can be done with it.
Finally we will look at some critical tests of the hypothesis that it is reliable.
(Actually the hypothesis will be that it is unreliable, but we will disprove it.)
Consider first a “normal” atom of carbon.
The other versions of carbon we will see
are perfectly real and in no way
“abnormal”, except that they do not have
the simplest predictable nuclear structure.
The atomic number of this atom is 6 (as in
all carbon) because it has 6 (+) protons,
represented here by purple balls. The
atomic mass is 12 because there are 12
total mass units – 6 (+) and 6 (electrically
neutral) neutrons (n).
electron – e-
neutron – (n)
proton – (+)
There are 6 electrons to balance the 6
protons in two shells – 2 in an inner and 4
in an outer shell. These are interesting
che4mically, but not in terms of the
nuclear reactions we will examine, so this
is the last time we will show them.
Remember that they are there even if we
don’t show them in our diagrams.
We’ve seen that “ordinary” carbon has an
atomic mass of 12 because it has 12 massbearing nuclear particles. This version is
designated 12C.
Other versions of carbon exist, differing not in
their number of protons (which is what makes
them carbon in the first place) but in their
mass -- the total number of nuclear particles.
Because the proton number must be the
same in any version of carbon, the difference
is therefore the number of neutrons. One
fairly uncommon version has one additional
neutron and is therefore 13C.
The version we will examine has two
additional neutrons and is therefore 14C.
Different mass versions of the same element
are called isotopes. 14C is a radioactive
isotope. This means it is unstable and has a
high probability of being modified by a
process we call radioactive decay.
In the first geology course we usually introduce protons as particles with no charge, but certain
types of nuclear reactions indicate that this is not exactly true. In such reactions either a
neutron can be given a positive charge (making it a proton) or a proton can be neutralized
(making it a neutron). Both reactions also involve a small, massless particle of charge (-1).
This of course is an electron. So a neutron has the same mass as a proton because it is a
proton, but with it’s charge neutralized by a contained electron.
a neutron is …
(+)
neu
a neutralized
proton
(-)
There are three common ways that a radioactive
isotope decays. 14C does it in a way called beta
decay.
beta (= e-)
14C
One of the neutrons spontaneously (and randomly)
emits a beta particle which is, in effect, an
electron. As a result, that neutron is no longer
neutral, but positive.
Recall that an electron has effectively no mass.
The particle that remains in the nucleus therefore
has the same mass as ever, but is now positive. In
other words it is a proton. This means that the
atom now has 7 rather than 6 protons. (The outer
e- shell will add an electron to balance this charge.)
An atom with 7 protons (atomic number 7) is not
carbon, but rather nitrogen. One element has
transformed into another – 14C is now 14N!
14N
In this instance C is the parent and N the daughter
isotope.
The atmosphere is mostly nitrogen and in its upper part
(the ionosphere) the N atoms are constantly bombarded
by and are “absorbing” ionized particles from the sun.
This is the solar wind. and it doesn’t reach the surface
(and wreck living tissue) partly because of this process of
“absorption” in the ionosphere.
e14N
Some of the solar wind particles are electrons and they
can interact with 14N in such a way that the previous
process is reversed – a proton “absorbs” an electron,
neutralizing its positive charge and making it a neutron.
This is electron capture.
Now the atom has 6 protons and 8 neutrons so it is no
longer 14N but has changed to 14C.
Electron capture in this case has created a radioactive
atom that is now subject to beta decay, and so can
produce 14N again!
This ability to undo decay and recreate the original atom,
then cycle through another decay is possible in some
radioactive isotopes but not all. We will come back to this
point later as we discuss tests of the hypothesis of
radioactive dating.
14C
For the final type of decay we will use a
hypothetical atom of 6 protons to show
the process, but be warned – carbon
atoms themselves do not experience
this type of decay.
I use a small atom schematically to
avoid having to draw (and have you
count the particles in) a very large one.
HYPOTHETICAL
SMALL PARENT
ATOM THAT IS NOT
CARBON!!!!
In the final decay type a very large nucleus may
eject four mass particles – two each of protons
and neutrons – as a unit. this is effectively a
helium (4He) nucleus. These large particles are
potentially very damaging and carry a lot of
energy. This is where most of the heat that
Rutherford discovered comes from.
Alpha decay leaves the parent isotope 4 mass
units lighter and two atomic numbers lower. If
carbon did decay this way (it does not – don’t
forget it) the daughter isotope would have atomic
number 4 and atomic mass 8. It would be 8Be in
other words.
4He
HYPOTHETICAL
SMALL DAUGHTER
ATOM THAT IS NOT
BERYLLIUM!!!!
nucleus (or “alpha particle”)
(or “alpha ray”) emitted
There are a fairly large number of radioactive isotopes in the universe, but for now
we are only interested in a small percentage of them. Some of the larger atoms
(like certain Uranium (U) isotopes) do not decay directly to their daughter (a lead
(Pb) isotope in the case of U), but do so through a series of alpha, beta, e- capture
steps.
Whereas the total pathway from U to Pb has an exceptionally long half-life, the
intermediates have much shorter ones. They decay at rates measurable in realtime in a laboratory. It was by studying these decay events that Rutherford
discovered the principle of the decay constant. This is an easily determined
value from which can be calculated the half life of even very long-lived isotopes.
This illustrates very nicely an idea we presented on day 1 – how to know
something. We know the half-lives of many short-lived isotopes from direct
observation. We know that the decay constant in each case can be used to
predict that half-life. Therefore we “know” that the decay constant of U or some
other long-lived isotope can be predicted from its decay constant.
That is, there is an intermediate (but mathematically provable) intermediate step
required to know what the half-life of a long-lived isotope is. We do not exist,
either individually or collectively, for long enough to measure it directly.
Take-Home Message
• Certain configurations of atomic nuclei are inherently unstable.
We call atoms that have these configurations radioactive
isotopes.
• These atoms are subject to spontaneous “decay” which stabilizes
the structure, either in one or several steps.
• beta decay occurs when a neutron expels an electron, leaving it
(+), and therefore a proton. This raises the atomic number by 1
but doesn’t change the atomic mass. (14C to 14N)
• electron capture is the opposite. A proton absorbs an electron
and becomes a neutron. This lowers the atomic number without
changing the atomic mass. (14N to 14C)
• alpha decay occurs when the nucleus emits 2 protons and 2
neutrons – a helium nucleus or alpha particle. (U to Pb involves
several of these, as well as some betas).
• The half-lives of even very long-lived isotopes can be determined
by calculation from their easily determined decay constants.