Download Polarimetry in Astrophysics and Cosmology

POLARIMETRY IN ASTROPHYSICS AND
COSMOLOGY
by
Lingzhen Zeng
A dissertation submitted to The Johns Hopkins University in conformity with the
requirements for the degree of Doctor of Philosophy.
Baltimore, Maryland
June, 2012
c Lingzhen Zeng 2012
All rights reserved
Abstract
Astrophysicists are mostly limited to passively observing electromagnetic radiation from a distance, which generally shows some degree of polarization. Polarization often carries a wealth of information on the physical state and geometry of the
emitting object and intervening material. In the microwave part of the spectrum,
polarization provides information about galactic magnetic fields and the physics of
interstellar dust. The measurement of this polarized radiation is central to much
modern astrophysical research.
The first part of this thesis is about polarimetry in astrophysics. In Chapter 1,
I review the basics of polarization and summarize the most important mechanisms
that generate polarization in astrophysics. In Chapter 2, I describe the data analysis
of polarization observation on M17 (a young, massive star formation region in the
Galaxy) from Caltech Submillimeter Observatory (CSO) and show the physics that
we learn about M17 from the polarimetry.
Polarimetry also plays an important role in modern cosmology. Inflation theory
predicts two types of polarization in the Cosmic Microwave Background (CMB) radiation, called E-modes and B-modes. Measurements to date of the E-mode signal are
consistent with the predictions of anisotropic Thompson scattering, while the B-mode
signal has yet to be detected. The B-mode power spectrum amplitude can be parameterized by the relative amplitude of the tensor to scalar modes r. For the simplest
inflation models, the expected deviation from scale invariance (ns = 0.963 ± 0.012) is
coupled to gravitational waves with r ≈ 0.1. These considerations establish a strong
motivation to search for this remnant from when the universe was about 10−32 seconds
ii
old.
The second part of this thesis is about the Cosmology Large Angular Scale Surveyor (CLASS) experiment, that is designed to have an unprecedented ability to
detect the B-mode polarization to the level of r ≤ 0.01. Chapter 3 is an introduction
to cosmology, including the big bang theory, inflation, ΛCDM model and polarization of the CMB radiation. Chapter 4 is about CLASS, including science motivation,
instrument optimization and lab testing.
Advisor: Prof. Charles L. Bennett
Second reader: Prof. Tobias Marriage
iii
Acknowledgements
The work described in this thesis would not have been possible without the support
of many people. Foremost, I would like to express my sincere gratitude to my advisor
Prof. Chuck Bennett for the continuous support of my Ph.D study and research, for
his patience, motivation, enthusiasm, and immense knowledge. His guidance helped
me in all the time of research and writing of this thesis. I could not have imagined
having a better advisor and mentor for my Ph.D study.
Besides my advisor, I would like to thank Dave Chuss. In many research projects,
I have been aided for many years by him. Dave is patient and always ready to discuss
whatever problems are on my mind. I would like to thank Prof. Giles Novak, who
offered me much advice and insight on the millimeter/submillimeter polarimetry. I
will miss the time when we worked together on Mauna Kea summit.
I gratefully acknowledge Prof. Toby Marriage for his valuable advice in lab discussions, supervision on lab instrument development. I would also like to thank Toby
for his great help in my job application.
I would like to thank David Larson and Joseph Eimer. We worked together for
many years and have so many useful discussions and collaborations.
My sincere thanks also goes to Ed Wollack, John Vaillancourt, George Voellmer,
Gary Hinshaw, John Karakla, Karwan Rostem, Tom Essinger-Hileman and Paul Mirel
for offering me help and discussions on the various research projects.
I thank my fellow graduate/undergraduate students in the research group at Johns
Hopkins University: Dominik Gothe, Zhilei Xu, Aamir Ali, Dave Holtz, Connor Henley and Tiffany Wei for the fun and proud of working together on the CLASS project.
It is a pleasure to thank my friends at JHU for making my life fun: Jiming Shi,
iv
Jianjun Jia, Jun Wu, Zhouhan Liang, Jian Su, Sunxiang Huang, Yuan Yuan, Longzhi
Lin, Hao Chang, Di Yang, Xin Guo, Jie Chen, Xiulin Sun, Jianhua Yu, Xin Yu, Wen
Wang, Hui Gao, Jinsheng Li, Jiarong Hong and Yuan Lu. I am grateful to many
others for making my time at JHU enjoyable. Unfortunately, there are too many to
name individually.
I would also like to thank my undergraduate classmates: Huaze Ding, Xiao Hu
and Jun Li for our longtime friendship. I wish all of you the best in the future.
Last but not the least, I would like to thank my family: my parents Xiangxiong
Zeng and Qiuying Li, for giving birth to me at the first place and supporting me
spiritually throughout my life, and my sister Lingfang Zeng and brother Lingyao
Zeng, for their understanding and support in so many years.
v
Contents
Abstract
ii
Acknowledgements
iv
List of Tables
ix
List of Figures
x
I
1
Polarimetry in Astrophysics
1 Introduction to Polarization in Astrophysics
1.1 Plane Wave . . . . . . . . . . . . . . . . . . . . . . .
1.2 Stokes Parameters . . . . . . . . . . . . . . . . . . .
1.3 Poincaré Sphere . . . . . . . . . . . . . . . . . . . . .
1.4 Polarization in Astrophysics . . . . . . . . . . . . . .
1.4.1 Synchrotron Emission . . . . . . . . . . . . .
1.4.2 Thermal Dust Emission and Absorption . . .
1.4.3 Examples of Polarization from Absorption and
1.4.4 Anomalous Dust Emission . . . . . . . . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
Scattering
. . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
2 Submillimeter Polarimetry of M17
2.1 Introduction to Submillimter Polarimetry . . . . . . . . . . . . . . . .
2.2 Polarimetry at Caltech Submillimeter Observatory . . . . . . . . . . .
2.3 SHARP Data Pipeline . . . . . . . . . . . . . . . . . . . . . . . . . .
2.4 Introduction to M17 . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.5 M17 Polarimetry Results . . . . . . . . . . . . . . . . . . . . . . . . .
2.5.1 General Results . . . . . . . . . . . . . . . . . . . . . . . . . .
2.5.2 Polarization Spectrum . . . . . . . . . . . . . . . . . . . . . .
2.5.3 Spatial Distribution of Magnetic Field and Polarization Spectrum
2.5.4 Conclusion . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
vi
2
2
3
7
8
8
10
13
15
16
16
17
20
22
23
23
27
30
38
II
Polarimetry in Cosmology
39
3 Introduction to Polarization in Cosmology
3.1 The Big Bang Theory . . . . . . . . . . . . . . . . . . . . . .
3.1.1 The Expanding Universe–Hubble’s Law . . . . . . . . .
3.1.2 Big Bang Nucleosynthesis (BBN) . . . . . . . . . . . .
3.1.3 The Cosmic Microwave Background (CMB) Radiation
3.1.4 Other Evidence . . . . . . . . . . . . . . . . . . . . . .
3.2 Cosmic Inflation . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2.1 The Structure Problem . . . . . . . . . . . . . . . . . .
3.2.2 The Flatness Problem . . . . . . . . . . . . . . . . . .
3.2.3 The Horizon Problem . . . . . . . . . . . . . . . . . . .
3.2.4 The Magnetic Monopole Problem . . . . . . . . . . . .
3.3 ΛCDM Cosmological Model . . . . . . . . . . . . . . . . . . .
3.3.1 Cosmological Principles and FLRW metric . . . . . . .
3.3.2 Einstein Field Equations and Friedmann Equation . . .
3.3.3 Best-fit ΛCDM Model Parameters . . . . . . . . . . . .
3.4 The Cosmic Microwave Background Radiation . . . . . . . . .
3.4.1 The CMB Anisotropy . . . . . . . . . . . . . . . . . . .
3.4.2 The CMB Polarization . . . . . . . . . . . . . . . . . .
4 The Cosmology Large Angular Scale Surveyor (CLASS)
4.1 Scientific Overview . . . . . . . . . . . . . . . . . . . . . .
4.2 Sensitivity Calculation and Bandpass Optimization . . . .
4.2.1 Sensitivity Calculation . . . . . . . . . . . . . . . .
4.2.2 Bandpass Optimization . . . . . . . . . . . . . . . .
4.3 The Variable-delay Polarization Modulator . . . . . . . . .
4.3.1 Polarization Transfer Function . . . . . . . . . . . .
4.3.2 VPM Grid Optimization . . . . . . . . . . . . . . .
4.3.3 VPM Mirror Throw Optimization . . . . . . . . . .
4.3.4 VPM Efficiency . . . . . . . . . . . . . . . . . . . .
4.3.5 Current Status . . . . . . . . . . . . . . . . . . . .
4.4 CLASS Optics . . . . . . . . . . . . . . . . . . . . . . . . .
4.5 Smooth-walled Feedhorn . . . . . . . . . . . . . . . . . . .
4.5.1 Smooth-walled Feedhorn Optimization . . . . . . .
4.5.2 Smooth-walled Feedhorn for CLASS . . . . . . . . .
4.6 CLASS Detectors . . . . . . . . . . . . . . . . . . . . . . .
4.6.1 Focal Plane . . . . . . . . . . . . . . . . . . . . . .
4.6.2 TES Bolometers . . . . . . . . . . . . . . . . . . . .
4.7 Lab Set up for Detector Testing . . . . . . . . . . . . . . .
4.7.1 Cryostat . . . . . . . . . . . . . . . . . . . . . . . .
4.7.2 Thermometry . . . . . . . . . . . . . . . . . . . . .
vii
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
40
40
40
41
42
42
43
43
44
44
44
45
45
47
49
54
56
57
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
62
64
67
68
71
79
80
81
83
89
91
92
98
98
102
111
111
113
116
116
118
4.7.3
4.7.4
Cryostat Performance . . . . . . . . . . . . . . . . . . . . . . 118
Detector Readout . . . . . . . . . . . . . . . . . . . . . . . . . 119
A M17 Polarization Data
A.1 Polarziation Spectrum:
A.2 Polarziation Spectrum:
A.3 Polarziation Spectrum:
A.4 Polarziation Spectrum:
A.5 Polarization Vectors .
450 um vs
450 um vs
450 um vs
450 um vs
. . . . . .
60 um . .
100 um .
350 um at
350 um at
. . . . . .
. . . . . . . . . .
. . . . . . . . . .
RA > 18h 17m 30s
RA < 18h 17m 30s
. . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
125
125
127
129
130
132
B Blackbody Radiation
136
C NEP of Photons in a Blackbody Radiation Field
138
D A Low Cross-Polarization Smooth-Walled Horn with Improved Bandwidth
140
D.1 Smooth-walled Feedhorn Optimization . . . . . . . . . . . . . . . . . 141
D.1.1 Beam Response Calculation . . . . . . . . . . . . . . . . . . . 141
D.1.2 Penalty Function . . . . . . . . . . . . . . . . . . . . . . . . . 142
D.1.3 Feedhorn Optimization . . . . . . . . . . . . . . . . . . . . . . 143
D.2 Feedhorn Fabrication and Measurement . . . . . . . . . . . . . . . . . 145
D.3 Conclusion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 148
E CLASS 40 GHz Feedhorn Profile
153
F Lab Cryostat Thermometry Codes
159
Vita
189
viii
List of Tables
2.1
2.2
SHARP Instrument Specifications . . . . . . . . . . . . . . . . . . . .
M17 Polarization Spectrum Data . . . . . . . . . . . . . . . . . . . .
19
30
3.1
Best-fit ΛCDM Model Parameters . . . . . . . . . . . . . . . . . . . .
50
4.1
4.2
4.3
4.4
4.5
4.6
4.7
4.8
4.9
CLASS Scientific Overview . . . . . . . . . . . .
CLASS Detector Parameters . . . . . . . . . . .
CLASS VPM Mirror Throw Optimization . . .
CLASS Optics Overview . . . . . . . . . . . . .
CLASS 40 GHz Feedhorn Requirements . . . .
Feedhorn Profile Approximation (in Millimeters)
Feedhorn Performance . . . . . . . . . . . . . .
Beam Parameters . . . . . . . . . . . . . . . . .
Cryostat Thermometry Readout . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
66
70
88
94
102
104
105
110
122
D.1 Spline Approximation to Optimized Profile (in Millimeters) . . . . . . 148
D.2 Beam Parameters . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 150
ix
List of Figures
1.1
1.2
1.3
1.4
1.5
2.1
2.2
A simple plane wave. The electric (E, in x-z plane) and magnetic field
(B, in y-z plane) is perpendicular to each other and to the direction of
propagation (z). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Polarization ellipse. It shows the (ξ, η) coordinates with respect to the
(x, y) coordinates and the definitions of orientation angle ψ, ellipticity
angle χ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Poincaré sphere, defining the polarization in spherical coordinates. It
also shows the relation between (Q, U, V ) and (Ip , χ, ψ) [1]. . . . . .
CMB foreground radiation in WMAP bands [2]. The synchrotron radiation dominates the low frequency range below 60 GHz. Radiation
from dust contributes mostly above 70 GHz. . . . . . . . . . . . . . .
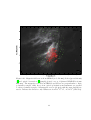
Starlight polarization vectors in Galactic coordinates. The upper panel
shows polarization vectors in local clouds. The polarization averaged
over many clouds in the Galactic plane is shown in the lower panel.
The magnetic field is parallel to the polarization angle. . . . . . . . .
NEFD350 µm measurements (points) from Jan 2003 compared to theoretical expectation (solid line) from equation 2.1 [3]. The performance
is about 1 Jy s1/2 for τ225 GHz = 0.05. . . . . . . . . . . . . . . . . . .
The polarization splitting optics of SHARP [4] for reconstituting the
image with an offset between the two polarization components. Left:
The expanding beam from the CSO focus is reflected by P1 (paraboloid),
F1 (flat mirror), through the HWP (half wave plate), and reaches the
XG (crossed grid), where the polarization radiation is separated into
two orthogonal (horizontal and vertical) components. Right: View toward the CSO focus. The vertical and horizontal components undergo
further reflections by a series of mirrors and grids, and are displaced
laterally at the BC (beam combiner), before being directed toward
SHARC II. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
x
4
5
7
9
14
18
19
2.3
Flow chart of “SharpInteg”. It starts by masking the raw data file
with an “rgm” file. Then, it demodulates the chopping to calculate the
chopped data. After applying the relative data gain factor between the
horizontal and vertical array, it calculates the I, I-error, Q, Q-error, U
and U-error components and saves them into a new file. . . . . . . . .
2.4 Flow chart of “Sharpcombine”. It applies τ and telescope pointing
correction, background subtraction (BS), instrument polarization (I.P.)
subtraction and polarization angle rotation to sky coordinates (Rot) to
each sub-map before it combines them into a large map and smooths it.
2.5 M17 is a premier example of a young, massive star formation region
in the Galaxy. Left: A M17 image from my 80 mm aperture optical
telescope. Right: A false color image from Spitzer GLIMPSE (red: 5.8
um; green: 4.5 um; blue: 3.6 um.) [5]. . . . . . . . . . . . . . . . . . .
2.6 A M17 model from [6]. The system can be described as a central cluster
of stars surrounded by successive layers of H+ , H0 , and H2 gas, that
expanding with different velocities to the outer side of the cloud. . . .
2.7 M17 polarization fraction vectors are plotted over the 450 um uncalibrated flux map. Thick vectors are detected with greater than or equal
to 3σ level and thin vectors are between 2σ and 3σ level. The circle on
the bottom right shows the SHARP beamsize. Some parts of the flux
map is removed due to high noise levels. Offsets are from 18h 17m 32s ,
-16◦14′ 25′′ (B1950.0). . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.8 Histogram of M17 polarization fraction. This distribution includes all
vectors at greater or equal to than 2σ level. All vectors greater than
10% are 2σ vectors. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.9 Histogram of M17 polarization angle. Polarization angles are measured
from north to east. The resulting net magnetic field is almost parallel
to the RA direction. . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.10 Magnetic field vectors from SHARP (red, 450 um), Stokes (green,100
um) [7] and optical observation [8] (purple) plotted on top of Spitzer
GLIMPSE 8.00 um flux map. The magnetic vectors from SHARP
and Stokes are perpendicular to their polarization angles, while those
from optical polarization measurement are parallel to their polarization
angles. All magnetic vectors (plotted with the same length) are used
to indicate the direction only. Offsets are from 18h 17m 32s , -16◦14′ 25′′
(B1950.0). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.11 The common area (green shadow) for polarization spectrum analysis.
It is between 18h 17m 30s and 18h 17m 37s in Ra (B1950), −16◦ 16′20′′ and
−16◦ 13′ 00′′ in Dec (B1950). The selected polarization vectors are at
60 µm (yellow), 100 µm (green), 350 µm (blue) and 450 µm (red).
Background is the 450 µm flux map. Offsets are from 18h 17m 32s , 16◦ 14′ 25′′ (B1950.0). . . . . . . . . . . . . . . . . . . . . . . . . . . .
xi
20
21
22
24
25
26
26
28
29
2.12 Polarization spectrum of some popular interstellar molecular clouds [9].
The median polarization ratio are normalize by the value at 350 µm.
In contrast to the results from other clouds, our work shows that, the
M17 has lower median polarization at 450 µm than at 350 µm. The
polarization spectrum falls monotonically from 60 µm to 450 µm. . .
2.13 Magnetic vectors from SHARP plotted over the [21 cm]/[450 µm] flux
ratio map, showing that the shock front is passing through the cloud.
The contour levels are {0.1, 0.3, 0.5, 0.7, 0.9}. The “X” axis is defined
by fitting contour level = 0.1. The new “X-Y” coordinate system is
about 66.3◦ with respect to the “Ra-Dec” coordinates. The shock is
following the “-Y” direction. The “y=0” and “y=-50 arcsec” lines separate the cloud into “post-shocked” (y > 0), “shock front” (-50 < y < 0)
and “pre-shocked” (y < -50) regions. The polarization directions and
magnitudes in these regions are different (figure 2.14 and 2.15). The
magnetic fields in the dense cloud (can also be seen in figure 2.10) at
the top of the map survive the windswept. Offsets are from 18h 17m 32s ,
-16◦14′ 25′′ (B1950.0). . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.14 Correlation between polarization angle and the Y direction (zero at
18h 17m 32s , −16◦ 14′ 25′′ ), showing a linear relationship. The “postshocked” region is at y > 0 and the “pre-shocked” region is at y < −50
arcsec. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.15 Correlation between polarization fraction and Y direction (zero at
18h 17m 32s , −16◦ 14′ 25′′ ), showing a “U” like shape. The polarization
fraction is higher at the “post-shocked” region at y > 0 and the “preshocked” region at y < −50 arcsec. . . . . . . . . . . . . . . . . . . .
2.16 Magnetic field vectors (red) and intensity contours of SHARP (green,
levels = {0.0, 0.2, 0.4, 0.6, 0.8, 1.0}) are over plotted on the 21 cm
absorption-line contour and the ratio of neutral HI (NHI) column density to the spin temperature Tspin distribution map in the 17.5-22 km/s
velocity area from [6]. This velocity component is correlated with the
“post-shocked” and part of “shock front” region. The NHI/Tspin density at the dense cloud region (see figure 2.13) is low. . . . . . . . . .
2.17 The [450 µm]/[350 µm] polarization ratio vectors over plotted on the
[21 cm]/[450 µm] flux ratio map with contour levels = {0.1, 0.3, 0.5,
0.7, 0.9}. The blue (red) vectors represent P450 < (>) P350 . The
length of the 2% bar at bottom left is equivalent to P450 /P350 = 1.0.
The directions of the vectors are parallel to their polarization angles.
Offsets are from 18h 17m 32s , -16◦14′ 25′′ (B1950.0). . . . . . . . . . . .
2.18 The [450 µm]/[350 µm] polarization ratio vectors and 450 µm intensity
contours of SHARP (green, levels = {0.0, 0.2, 0.4, 0.6, 0.8, 1.0}) over
plotted on the Fig.1 from [7]. The blue vectors is found to be correlated
with the [OI] line, which is a tracer for the atomic gas. . . . . . . . .
xii
31
33
34
34
35
36
37
3.1
3.2
3.3
3.4
3.5
4.1
4.2
4.3
4.4
Timeline of the universe. The CMB radiation from the last scattering
surface (LSS) when the universe is about 380,000 years old with the
temperature of about 3,000 K [10]. . . . . . . . . . . . . . . . . . . .
The internal linear combination map from WMAP [11], showing the
all sky CMB temperature anisotropy. . . . . . . . . . . . . . . . . . .
The angular power spectrum from WMAP [12], showing the detection
of the first three peaks. The first peak is at ℓ ≈ 220, corresponding to
an angular scale of about 1◦ . . . . . . . . . . . . . . . . . . . . . . . .
Left: Quadrupole polarization from Thomson scattering of the CMB
photons with free electrons. Right: The E and B mode patterns. The
E-modes are curl-free components with no handedness. The B-modes
are curl components with handedness. . . . . . . . . . . . . . . . . . .
Plots of signal for TT (black), TE (red ), and EE ( green). The notyet-detected BB (blue dots) signal is from a model with r = 0.3. The
BB lensing signal is shown as a blue dashed line. The foreground model
for synchrotron plus dust emission is shown as straight dashed lines [13].
Two-dimensional joint marginalized constraint (68% and 95% CL) on
scalar spectral index (ns ) and tensor to scalar ratio (r), derived from
the data combination of WMAP + BAO + H0 [14]. Three linear fits
are from different simple inflation models. . . . . . . . . . . . . . . .
The background is the WMAP 7 year all sky Q band polarization map
in Galactic coordinates showing the sky coverage of CLASS experiment. Observing from the Atacama Desert in Chile, CLASS covers
∼ 65.1% of the sky above 45◦ elevation. Excluding the Galactic mask
area, the visible sky left is ∼ 46.8% (bright region). The dark circle at
the south pole is about 22◦ in radius. Figure courtesy of David Larson.
CLASS instrument overview for the 40 GHz band. The instrument
consists a front-end variable-delay polarization modulator, catadioptric
optic system and a field cryostat. The lenses are cooled to about 4 K
and the smooth-walled feedhorn-coupled TES bolometer array operates
at 100 mK. Figure courtesy of Joseph Eimer. . . . . . . . . . . . . . .
CLASS wavebands and sensitivity curve from [15]. Left: The frequency
bands of CLASS are chosen to straddle the Galactic foreground spectral minimum and to minimize atmospheric effects (see section 4.2.2).
Right: The CLASS sensitivity curve, shown by the dashed curve along
the shaded boundary, is the 1σ limit for each l and assumes 3 years
of observing with a conservative 50% efficiency for down-time (see section 4.2.1). CLASS has the sensitivity to definitively detect B-modes
at the cosmologically interesting limit of r ∼ 0.01. . . . . . . . . . . .
xiii
55
56
58
59
60
63
64
65
68
4.5
Annual variation of the Precipitable Water Vapor (PWV) content at
Chajnantor, based on 10 years of site testing. Conditions are worse
during the winter from the end of December to early April. The expected median PWV for the rest of the year is around 1 mm, while
conditions of PWV < 0.5 mm can be expected up to 25% of the time
[16]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.6 Atmospheric transmission and brightness temperature at CLASS site
from 5 to 1000 GHz. ATM parameters: ground temperature = 275 K,
ground pressure = 558 mb, PWV = 1.0 mm, elevation = 45◦ , altidude
= 5180 m. ATM version: atm2011 03 15.exe. . . . . . . . . . . . . . .
4.7 Top: the CMB signal (equation 4.20) and Bottom: atmospheric noise
source (equation 4.16) for the relative signal-to-noise ratio calculation
(equation 4.21). The red, green and blue lines shows our optimized
bandwidth for 40, 90 and 150 GHz band: (30.3 GHz - 40.3 GHz), (77.3
GHz - 108.3 GHz) and (126.8 GHz - 164.3 GHz). . . . . . . . . . . .
4.8 The 2-D plot of relative signal-to-noise ratio (equation 4.22) from 0 to
200 GHz showing our optimization results. The cross points of red,
green and white lines are the locations of the local maxima. For the
40 GHz band, we only search for the maximum in the range of ν > 30
GHz. The coordinates are (30.3, 40.3), (77.3, 108.3) and (126.8, 164.3).
4.9 As shown in Poincaré sphere, VPM modulates between Q and V , while
the HWP mix Q and U. In the case of VPM, the residuals due to the
spectral effects (shown in blue) are a function of measurable modulation parameters. Figure courtesy of David Chuss. . . . . . . . . . . .
4.10 VPM modulates polarization by introducing a controlled variable path
difference between two orthogonal linear polarizations. Dots show the
component with polarization angle parallel to the grid; Double arrow
show that with angle perpendicular to the grid. By moving the mirror up and down, VPM introduces a path difference x(t) = 2d(t)cosθ
between these two orthogonal polarization components. . . . . . . . .
4.11 The wire grid performances for two different wavelengths from a simulation [17]. In the limit of g/λ ≪ 1, a sinusoidal form for Stokes Q
is in good agreement with an ideal grid (equation 4.29). The VPM
reflection phase delay differs from the free-space grid-mirror delay if
the conditions are changed. . . . . . . . . . . . . . . . . . . . . . . .
4.12 The contour plot of relative signal-to-noise ratio for Stokes Q, calculated from equation 4.42 with cosine chopping mode. This plot is for
the 40 GHz band (33 GHz to 43 GHz, λ0 = 7.89 mm). The maximum
is at (0.19 λ0 , 0.13 λ0 ) with the peak signal-to-noise ratio scaled to be
1.00. There are 4 other local maxima nearby: (0.19 λ0 , 0.39 λ0 ), (0.44
λ0 , 0.13 λ0 ), (0.44 λ0 , 0.39 λ0 ) and (0.27 λ0 , 0.26 λ0 ). Details are listed
in table 4.3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
xiv
73
74
77
78
79
80
82
86
4.13 The contour plot of relative signal-to-noise ratio for Stokes Q, calculated from equation 4.42 with linear chopping mode. This plot is for
the 40 GHz band (33 GHz to 43 GHz, λ0 = 7.89 mm). The maximum
is at (0.46 λ0 , 0.16 λ0 ) with the peak signal-to-noise ratio scaled to be
1.00. There are 2 other local maxima nearby: (0.63 λ0 , 0.19 λ0 ) and
(0.45 λ0 , 0.42 λ0 ). Details are listed in table 4.3. . . . . . . . . . . . . 87
4.14 VPM efficiency calculated from equation 4.55. The efficiency drops
quickly from r = 1.0 to r = 5.0 and becomes almost flat after r > 10.
The noise at large r is due to the rounding in the numerical calculations. 92
4.15 Photo of the prototype VPM grid. The wires are glued on an aluminium box frame with over 2 tons of stretch force. The diameter of
the flattener ring is 50 cm. The wire diameter, 2a, is 63.5 µm, with
wire pitch, g = 200 µm. 2a/g = 1/3.15 ≈ 1/π. The flatness of the grid
is better than 50 µm. The total length of the wires is longer than 2
miles. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 93
4.16 Top: Drawings of CLASS 40 GHz optics. It consists of a front-end
VPM, two mirrors, two lenses, a Lyot stop, a vacuum window and two
infrared (IR) blocking filters. Bottom: Drawing and the ray trace of
the cooled optics. Units are in mm. Figure courtesy of Joseph Eimer.
95
4.17 Ray trace of CLASS 40 GHz optics. Basic parameters: VPM diameter
= 60.0 cm, effective focal length = 70.5 cm, f/2.0, focal plane diameter
= 27.0 cm, Lyot stop diameter = 30.0 cm, FOV = 18.0◦ , number of
pixels = 36. Figure courtesy of Joseph Eimer. . . . . . . . . . . . . . 96
4.18 Point spread diagram of CLASS 40 GHz optics from Zeemax. Each
diagram in this figure represents a separate direction on the sky. The
circles show the first Airy disk at the corresponding location. This
diagram shows that the optics is diffraction limited. Figure courtesy
of Joseph Eimer. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 97
4.19 Flow chart of smooth-walled feedhorn optimization. Optimization begins with a sin0.75 profile, the method from [18] is used to calculate
the beam patterns. The feedhorn profile was found by this multi-step
iterative solution with different thresholds in each step. . . . . . . . 101
4.20 CLASS 40 GHz feedhorn profile. The 10.00 mm long input waveguide
has a radius of 3.334 mm, with fc = 26.349 GHz. The length of
the feedhorn is 100.00 mm. The aperture is 35.828 mm. This is a
monotonic profile that allows a progressive milling technique. . . . . . 103
4.21 CLASS feedhorn performance from 30 to 50 GHz. The dashed lines
define the -30 dB line, and the waveband limit of 33 GHz and 43 GHz.
The cut off frequency is fc = 26.349 GHz. . . . . . . . . . . . . . . . 103
4.22 Beam patterns of the CLASS smooth-walled feedhorn within azimuth
angles of ±90◦ , from 33 GHz to 38 GHz. . . . . . . . . . . . . . . . . 106
xv
4.23 Beam patterns of the CLASS smooth-walled feedhorn within azimuth
angles of ±90◦ , from 39 GHz to 44 GHz. . . . . . . . . . . . . . . . .
4.24 Beam patterns of the CLASS smooth-walled feedhorn within azimuth
angles of ±15◦ , from 33 GHz to 38 GHz. . . . . . . . . . . . . . . . .
4.25 Beam patterns of the CLASS smooth-walled feedhorn within azimuth
angles of ±15◦ , from 39 GHz to 44 GHz. . . . . . . . . . . . . . . . .
4.26 The averaged cross-pol, return-loss and edge-taper plot for the tolerance calculation from 0 to 300 um. For each tolerance, these values
were from the average of 120 calculations. (The plots are noisy at large
tolerance, more calculation would be required to smooth the plots.) .
4.27 Section view of CLASS 40 GHz focal plane. It consists of a array of 36
smooth-walled feedhorns, waveguide adapter, detector mounting plate
and clips. The focal plane will operate at a temperature of 100 mK.
Figure courtesy of Thomas Essinger-Hileman. . . . . . . . . . . . . .
4.28 The feedhorn-couple TES bolometers set up [15] and prototype detector chip for the 40 GHz CLASS [19]. Left: The detector set up
showing the feedhorn, detector housing, detector chip and backshort.
Right: Photo of a 40 GHz prototype detector chip, showing the OMT,
Magic Tees, filters and TES membranes. . . . . . . . . . . . . . . . .
4.29 The electro-thermal circuit diagram of a TES bolometer (modified from
[20]). Left: Each pix with a heat capacity of C at temperature T is
connected by a thermal link G to a thermal source with a temperature
of Tbath . The total power to the pixel is Pγ + PJ − PG . Right: TES
is biased by IB = VB /RB , in the case of RB ≫ RSH . For R ≫ RSH ,
the TES is bias by V = IB RSH , then fluctuations of R will result in
fluctuation in current, which is read out by the inductor L and the
superconducting quantum interference device (SQUID) amplifier. . .
4.30 Section view of model 104 Olympus ADR cryostat showing mechanical
heat switch controller, vacuum valve, pulse tube (PT) head, 60 K plate,
4 K plate, adiabatic demagnetization refrigerator (ADR), high temp
superconducting leads for 4 T magnet, thermal shielding, and vacuum
jacket [21]. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.31 Left: The ADR and the He-4 refrigerator mounted on the 4 K plate of
the HPD cryostat in the experimental cosmology lab at Johns Hopkins
University. Photo courtesy of David Larson. Right: the rack-mounted
devices for cryostat thermometry. From top to bottom, they are, a
SRS SIM900 mainframe with 2 MUXs, a diode moniter and an AC
bridge, a front panel, a NI GPIB to Ethernet adapter, a Lakeshore 370
AC resistance bridge and two Keithley 2440 current sources. . . . . .
4.32 Cryostat cool down curves. It takes about 24 hours for the cryostat to
cool down to the state with stable temperature readouts. The typical
values of the thermometers are listed in table 4.9. . . . . . . . . . . .
xvi
107
108
109
111
112
113
114
117
119
120
4.33 ADR cooling curves at 100 mK, showing the magnet current versus
time of the ADR with the loads of from 2.0 to 10.0 µW. Based on
these curves, the FAA pill of the ADR have higher cooling capacities
at lower loads. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 121
4.34 The FLL block diagram for TES detector readout, showing the cold
electronics inside the cryostat and the warm electronics (MCE) [22]. . 123
4.35 This photo shows the Multi-Channel Electronics (MCE) mounted on
the wall the cryostat in the experimental cosmology lab at Johns Hopkins University. The MCE is connected to a data-acquisition computer
by a pair of fiber optic cables (the orange wires). Photo courtesy of
David Larson. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 124
A.1 60 um polarization vectors from Stokes ([23], Yellow) and the 450
um result from SHARP (smoothed to 22′′ resolution, Red), center at
18h 17m 32s ,-16◦14′ 25′′ (B1950.0). . . . . . . . . . . . . . . . . . . . . . 126
A.2 100 um polarization vectors from Stokes ([23], Green) and the 450um
result from SHARP (smoothed to 35′′ resolution, Red), center at 18h 17m 32s ,16◦ 14′ 25′′ (B1950.0). . . . . . . . . . . . . . . . . . . . . . . . . . . . 128
A.3 350 um polarization vectors from Hertz ([24]) and the 450 um result
from SHARP (smoothed to 20′′ resolution, Red), center at 18h 17m 32s ,16◦ 14′ 25′′ (B1950.0). Blue: Hertz vectors at RA > 18h 17m 30s , Green:
Hertz vectors at RA < 18h 17m 30s . . . . . . . . . . . . . . . . . . . . 131
B.1 The Planck, Wien and Rayleigh-Jeans spectrum of a 2.725 K black
body. The Wien limit is a good approximation at ν > 250 GHz and
the Rayleigh-Jeans limit works well below 20 GHz. . . . . . . . . . . 137
D.1 The initial, intermediate and final profiles are shown. All dimensions
are given in units of the cuttoff wavelength of the input circular waveguide. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 145
D.2 (Top) The maximum cross-polar response across the band is shown
for the three profiles in Figure D.1. Measurements of the maximum
cross-polarization are superposed. (Bottom) The reflected power measurements for the final feed horn are shown plotted over the predicted
reflected power for the initial, intermediate, and final feedhorn profiles.
Frequency is given in units of the cutoff frequency of the input circular
waveguide. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 146
D.3 A smooth-walled feedhorn operating between 33 and 45 GHz was constructed. The horn is 140 mm long with an aperture radius of 22 mm.
The input circular waveguide radius is 3.334 mm. . . . . . . . . . . . 149
xvii
D.4 The measured E-, H-, and diagonal-plane angular responses for the
lower edge (33 GHz), center (39 GHz), and upper edge (45 GHz) of
the optimization band are shown. The cross-polar patterns in the
diagonal plane are shown in the bottom three panels for each of the
three frequencies. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 151
D.5 The maximum cross-polar response of the prototype feedhorn is compared to other implementations of smooth-walled feedhorns. The data
presented have been normalized to the design center frequencies as
specified by the respective authors. . . . . . . . . . . . . . . . . . . . 152
F.1
F.2
F.3
F.4
F.5
F.6
SRS readout program front panel. . . . . . . . .
PID control program front panel. . . . . . . . .
Block diagram of the SRS readout program. . .
Block diagram of the PID control program. Part
Block diagram of the PID control program. Part
Block diagram of the PID control program. Part
xviii
. . . .
. . . .
. . . .
1 of 3.
2 of 3.
3 of 3.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
160
160
161
162
163
164
Part I
Polarimetry in Astrophysics
1
Chapter 1
Introduction to Polarization in
Astrophysics
Astrophysicists are mostly limited to passively observing electromagnetic radiation
from a distance. This radiation is most generally described by a specific intensity
as a function of sky direction (θ, φ), frequency (ν) and polarization state. The
polarization information is important for astronomy. Radiation from astronomical
sources generally shows some degree of polarization. Although it is usually only
a small fraction of the total radiation, the polarization component often carries a
wealth of information on the physical state and geometry of the emitting object and
intervening material. In the microwave part of the spectrum, polarization provides
information about galactic magnetic fields and the physics of interstellar dust. The
measurement of this polarized radiation is central to much modern astrophysical
research.
1.1
Plane Wave
Polarization describes the orientation and phase coherence of the oscillations of
electromagnetic waves. Specifically, the polarization of a wave is described by specifying the orientation of the wave’s electric field at a point in space. Polarization is
most usefully illustrated using the concept of a plane wave, a monochromatic wave
2
having planar wave fronts that are infinite in extent. Figure 1.1 shows a simple plane
wave with its electric component parallel to the x axis.
Generally, the electric field of a plane wave can be written as:
~ r , t) = (Ex , Ey , Ez ) = (Ax cos(kz − ωt + φx ), Ay cos(kz − ωt + φy ), 0)
E(~
(1.1)
where (Ax , Ay ) and (φx , φy ) are the amplitudes and phase offsets of the x and y
component of the electric field; ω is the angular frequency; k is the wave number.
In the x − y plane, equation 1.1 can be simplified as:
Ex = Ax sin(ωt − φx )
Ey = Ay sin(ωt − φy ).
(1.2)
By defining φ = φx − φy , equation 1.2 can be written into an elliptical form:
Ex Ey
Ex2 Ey2
+ 2 −2
cosφ = sin2 φ.
2
Ax Ay
Ax Ay
(1.3)
For different phase offsets, the polarization state varies. From equation 1.3, if
φ = mπ (where m = 0, ±1, ±2, ...), then Ex /Ax ± Ey /Ay = 0 (linear polarization); if
φ = (2m + 1)π/2 and Ax = Ay , then Ex2 + Ey2 = A2x (circular polarization); if φ 6= mπ,
then it will be an elliptical polarization. In the latter cases (circular and elliptical
polarization), the oscillations can rotate either towards the right (0 < φ < π) or
towards the left (−π < φ < 0) in the direction of propagation.
1.2
Stokes Parameters
The parameters {Ax , Ay , φ} above, used to describe polarization have different
units. In 1852, George G. Stokes defined a set of 4 parameters (the Stokes parameters) as a mathematically convenient alternative. For the monochromatic plane wave
described above, the Stokes parameters are:
I = A2x + A2y
Q = A2x − A2y
U = 2Ax Ay cosφ
V = 2Ax Ay sinφ
3
(1.4)
y
x
B
E
z
Figure 1.1: A simple plane wave. The electric (E, in x-z plane) and magnetic field
(B, in y-z plane) is perpendicular to each other and to the direction of propagation
(z).
where I is the intensity of the radiation; Q describes the horizontal and vertical
linear polarization components; U are the linear components with 45◦ angle and V
represents the circular polarization components.
Generally, the amplitude and phase offset of the radiation are time-dependent
stochastic variables {Ax (t), Ay (t), φ(t)} and the observed radiation is a partially co-
herent superposition of many waves. As a result, the Stokes parameters for a general
radiation field are defined as averaged quantities over a period in time:
I = hA2x (t) + A2y (t)i
Q = hA2x (t) − A2y (t)i
U = 2hAx (t)Ay (t)cosφ(t)i
V = 2hAx (t)Ay (t)sinφ(t)i
(1.5)
where angular brackets denote averaging over many wave cycles.
Useful relation can be derived among the stokes parameters. For purely monochromatic (coherent) radiation
I 2 = Q2 + U 2 + V 2 .
4
(1.6)
y
E
η
ψ
ξ
x
χ
Figure 1.2: Polarization ellipse. It shows the (ξ, η) coordinates with respect to the
(x, y) coordinates and the definitions of orientation angle ψ, ellipticity angle χ.
For the partially-coherent radiation, the previous equation becomes an inequality
I 2 ≥ Q2 + U 2 + V 2 .
(1.7)
We can define a total polarization fraction (degree of polarization)
p = (Q2 + U 2 + V 2 )1/2 /I.
(1.8)
Most sources of electromagnetic radiation contain a large number of emitters that
are not necessarily correlated with each other either in phase or direction and emit over
a limit bandwidth, in which case the light is said to be unpolarized (p = 0). If there is
partial correlation between the emitters, the light is partially polarized (0 < p < 1).
If the polarization is consistent across the bandwidth of detectors, partially polarized
light can be described as a superposition of a completely unpolarized component, and
a completely polarized one (p = 1).
Another way to describe polarization is to use the polarization ellipse parameters,
by giving the semi-major and semi-minor axes of the polarization ellipse, its orientation, and the sense of rotation (Figure 1.2). This method uses the orientation angle
(ψ, the angle between the major semi-axis of the ellipse and the x-axis.) and ellipticity angle χ = arccot(ǫ), where ǫ is the ellipticity (the major-to-minor-axis ratio of
5
the ellipse).
We have a transform between (Eξ , Eη ) and (Ex , Ey )
Ex = Eξ cosψ − Eη sinψ
Ey = Eξ sinψ + Eη cosψ
(1.9)
and
Ax = a0 ((cos2 χcos2 ψ + sin2 χsin2 ψ)1/2
Ay = a0 ((cos2 χsin2 ψ + sin2 χcos2 ψ)1/2
tanφx = tanχtanψ
tanφy = −tanχcotψ
(1.10)
−
→
where Eξ and Eη are the amplitudes of E along the semi-major and semi-minor axes,
−
→
a0 is the average amplitude of E .
From equation 1.2, equation 1.3, equation 1.9 and equation 1.10, we have
Eξ = a0 cosχsinωt
Eη = a0 sinχcosωt
(1.11)
and
Eξ2
Eη2
+
= 1.
(1.12)
a20 cos2 χ a20 sin2 χ
An ellipticity of zero (χ = π/2) or infinity (χ = 0) corresponds to linear polarization
and an ellipticity of 1 (χ = π/4) corresponds to circular polarization.
The relation between Stokes parameters and polarization ellipse parameters is:
I = a20
Q = a20 cos2χcos2ψ
U = a20 cos2χsin2ψ
V = a20 sin2χ
(1.13)
with the following inverse equations:
tan2ψ = U/Q
sin2χ = V /(Q2 + U 2 + V 2 )1/2 .
6
(1.14)
(V)
(U)
(Q)
Figure 1.3: Poincaré sphere, defining the polarization in spherical coordinates. It also
shows the relation between (Q, U, V ) and (Ip , χ, ψ) [1].
1.3
Poincaré Sphere
From equation 1.13, the polarization state can be described in spherical coordinates, by replacing a20 with Ip :
Q = Ip cos2χcos2ψ
U = Ip cos2χsin2ψ
V = Ip sin2χ
(1.15)
where Ip = (Q2 + U 2 + V 2 )1/2 is the polarization intensity, 2χ and 2ψ are other two
axes in the spherical coordinates.
Equation 1.15 makes use of a convenient representation of the last three Stokes
parameters as components in a three-dimensional vector space. The Poincaré sphere
is the spherical surface occupied by polarization states having a constant polarization:
7
 
Q

1 
S= 
U


Ip
V
(1.16)
The Poincaré sphere provides a convenient way of representing polarization and
representing how any given retarder (i.e. the VPM described in section 4.3) will
change the polarization form. The north and south poles of the sphere represent
left and right circular polarization (V ). The points on the equator correspond to
linear polarization state (Q and U). Other points on the sphere represent elliptical
polarizations. If an arbitrarily chosen point on the equator designates horizontal
polarization, then the point which locates 180◦ opposite to it designates vertical
polarization. A general point (Ip ) on the surface of the Poincaré sphere is specific in
terms of the longitude (2ψ) and the latitude (2χ). The factor of 2 before ψ represents
the fact that any polarization ellipse is indistinguishable from one rotated by 180◦ ,
and the factor of 2 before χ indicates that an ellipse is indistinguishable from one
with the semi-axis lengths swapped by a 90◦ rotation.
1.4
Polarization in Astrophysics
Many mechanisms generate polarized emission in astrophysics, including synchrotron emission, dust emission, absorption (extinction) and scattering, such as
starlight polarization and free-free (bremsstrahlung) emission from cloud edges. Additional polarized components like the anomalous emission from dust have also been
discovered.
1.4.1
Synchrotron Emission
Synchrotron emission arises from the acceleration of cosmic-ray electrons in magnetic fields. Based on the results of Cosmic Microwave Background (CMB) foreground
studies [2] (Figure 1.4), synchrotron radiation dominates at frequencies below 60 GHz
(≥ 5 mm).
8
Antenna Temperature ( K, rms)
K
100
Ka
85
%
Sy
nc
Q
Sk
y(
V
CMB Anisotropy
Kp
2
o 77 )
e-f tro % S
ree n
ky
Fre
hr
(K p
10
1
20
W
40
st
Du
0)
60
80
100
Frequency (GHz)
200
Figure 1.4: CMB foreground radiation in WMAP bands [2]. The synchrotron radiation dominates the low frequency range below 60 GHz. Radiation from dust contributes mostly above 70 GHz.
If the energy spectrum of cosmic-ray electrons can be expressed as a power-law
distribution:
N(E) ∝ E −γ
(1.17)
where γ is the electron power-law index, then the synchrotron flux density spectral
index (α) and synchrotron emission spectral index (β) are related to γ, by:
γ −1
2
γ+3
β=−
2
α=−
(1.18)
and we have the flux density S(ν) ∝ ν α and the brightness temperature T (ν) ∝ ν β .
Assuming N(E) and a uniform magnetic field, the resulting emission is strongly
polarized with fractional linear polarization:
psyn =
γ+1
γ + 7/3
(1.19)
and aligned perpendicularly to the magnetic field [25]. At microwave frequencies, the
synchrotron emission spectral index observed is β ≈ −3 [26], so that synchrotron
9
emission could have fractional polarization as high as psyn = 75% (equation 1.18
and equation 1.19), which is almost never observed. The main reason for that is the
magnetic field distribution and the electron energy distribution are not uniform in the
Galaxy. The line of sight and beam averaging effects reduce the observed polarization
fraction by averaging over different regions in the Galaxy. At low frequencies (below
a few GHz) Faraday rotation (∝ λ2 ) will also reduce the polarization fraction for a
sufficiently wide passband.
1.4.2
Thermal Dust Emission and Absorption
The dominant source of Galactic emission at far-infrared (far-IR) and submillimeter (SMM) wavelengths (100 GHz - 6000 GHz) is thermal emission from interstellar
dust grains at temperatures of 10 - 100 K. The spectrum of this radiation is generally modelled with one or more thermal components with different temperatures by
a frequency dependent emission:
I(ν) =
n
X
Ai ν βi Bν (Ti )
(1.20)
i=1
Where ν is frequency, n is the total number of thermal components, Ai , νi and Ti
are the coefficient, spectral index and temperature of component i, Bν is the Planck
blackbody function (equation B.1).
Multiple temperatures and spectral indices are often needed to model the intensity
spectrum at any single point on the sky. For example, The Galactic dust emission has
been modelled by a two temperature component model of T1 = 9.5 K with β1 = 1.7
and T2 = 16 K with β2 = 2.7 [27].
Dust Grain Alignment
The radiation from the dust grains that have been aligned by interstellar magnetic
fields is partially polarized. The alignment requires: (1) The small axis (symmetry
axis) with the largest moment of inertia of the grain to be aligned with the spin axis;
(2) The spin axis is then aligned with the local magnetic field [28, 29, 30, 31, 32].
10
(1) Internal Dissipation Consider a dust grain with rotational energy of
1
Erot = (Ix Ω2x + Iy Ω2y + Iz Ω2z )
2
(1.21)
where Ix < Iy < Iz are the principal axes of inertia and Ωx , Ωy , Ωz are the angular
velocities. Such a dust grain has an angular momentum,
J = (Ix2 Ω2x + Iy2 Ω2y + Iz2 Ω2z )1/2
(1.22)
Suppose the total angular velocity Ω is not parallel to any of the principal axes, then
periodic motions will be executed with respect to these axes, which will mechanically stress the grain by the alternating centrifugal forces. As a result, heat will be
generated at the expense of Erot . Since J will not change (conservation of angular
momentum), this requires an increase in the time-average value of Ω2z relative to Ω2y
(or Ω2y to Ω2x ). The dissipation will not stop until Ω2x = Ω2y = 0 and Ω2z = J 2 /Iz2 .
The internal dissipation of the rotational energy in a free rotator forces the angular
velocity Ω toward the axis with the largest moment of inertia Ωz [33].
(2) Barnett Dissipation In 1915, Barnett found the magnetization of an uncharged body when spun on its axis [34]. A paramagnetic or ferromagnetic body
rotating freely will develop spontaneously a magnetic moment M parallel to the axis
of rotation (Barnett Effect):
M = χΩ/γ
(1.23)
where Ω is the angular velocity, χ is the magnetic susceptibility and γ is the gyromagnetic ratio for the material. The Barnett effect can be explained by considering that
some of the angular momentum is transferred to the unpaired electrons thus aligning
the magnetic moments. In the case of a dust grain, if the initial Ω is not parallel
to any principal axis, it will precess in the grain coordinates. The magnetic moment
will lag behind the precession, which will cause a dissipation (Barnett Dissipation)
of the rotational energy Erot . As a result, Ω will become parallel to Ωz and the local
magnetic field.
There is a balance between the alignment of the symmetry and spin axis of dust
grains with magnetic field and the collisions between the grains and gas molecules.
11
In order for the dust grains to become aligned, the time scale of the alignment must
be shorter than the time scale of the damping of collision. This condition is satisfied
if the grains are rotating supra thermally, Erot ≫ kT . The torques produced by the
formation and subsequent ejection of H2 molecules from grain surfaces could spin up
the grain to the necessary speeds [35, 33].
Photons can also provide the necessary torques to spin up the grain [36, 37, 38, 39].
It has been suggested by observation that photons can produce a net torque on
irregularly shaped grains because they present different cross sections to right- and
left-hand circularly polarized photons [30]. Modern grain alignment theory favors
radiative torques over H2 torques as the mechanism by which grains achieve high
angular velocities and align with magnetic fields. The angular momentum of a grain
may flip suddenly because of thermal fluctuations. One reason for this is that the H2
torques will change direction when the spin vector flips, causing the grain to spindown [40, 41]. Due to these “thermal flipping” and “thermal trapping” effects, grains
smaller than 1 µm cannot reach supra thermal velocities [42]. However, this is not
the case for radiative torques because the helicity of a grain does not depend on its
orientation.
While other alignment mechanisms may dominate in some select environments
[43], the above mechanism is favored in conditions prevalent throughout most of the
interstellar medium (ISM). The result of this mechanism is to align the grains with the
longest axis perpendicular to the magnetic field. Since the grains will emit, and absorb, most efficiently along the long grain axis, polarization is observed perpendicular
to the magnetic field in emission, but parallel to the field in absorption (extinction).
Polarization by Emission from Elongated Dust
The polarization of radiation emitted from dust grains is parallel to the long axis
of the grain and perpendicular to the aligning magnetic field. The lower limit on the
column densities of the clouds that can be traced by emission polarimetry is set by
the earth atmosphere absorption and instrument sensitivity. In some dense clouds,
which the interstellar radiation cannot penetrate deeply into, the embedded stars can
12
still provide the necessary radiative torques to spin up the grains [44].
Polarization by Absorption from Elongated Dust
Polarization of starlight from ultraviolet to near-infrared (NIR) wavelengths is
mostly due to selective extinction by grains that have been aligned by a local magnetic field [28]. The polarization will be parallel to the magnetic field, since starlight
is preferentially absorbed along the long axis of the grain. Observations of starlight
polarization have proven to be a useful tool for tracing the magnetic field structure
in diffuse ISM regions [45, 46]. However, at high extinctions, photons are completely
absorbed. Even at moderate extinctions, polarization by absorption is not a reliable
tracer of the magnetic field due to the drop in grain alignment efficiency [47]. Polarization by absorption cannot be used to reliably trace magnetic field structure in
regions where the extinction (AV ) is greater than 1.3 [48].
1.4.3
Examples of Polarization from Absorption and Scattering
Starlight Polarization
The polarization of starlight was first observed by [49] and [50]. As concluded in
the last section, starlight polarization is only measureable in regions of low extinction
(AV less than a few magnitudes for near-infrared observations), where near-visible
photons can traverse the ISM. This makes it a feasible tool for inferring the Galactic
magnetic field. The extinction places a limit on the most distant stars for which
polarization can be observed. At high Galactic latitude, most stars observed with
polarization are within 1 kpc of the Sun. While at low latitude, this distance extends
to as far as 2 kpc [45, 51].
Figure 1.5 shows an analysis [51] using the data from [45]. The low latitude
stars have higher polarization fraction (p ≈ 1.7%) and extinctions (E(B − V ) ≈ 0.5
mag), while the high latitude stars have significantly lower values (p ≈ 0.5% and
E(B − V ) ≈ 0.15 mag). There is a strong alignment of net starlight polarization
13
Figure 1.5: Starlight polarization vectors in Galactic coordinates. The upper panel
shows polarization vectors in local clouds. The polarization averaged over many
clouds in the Galactic plane is shown in the lower panel. The magnetic field is
parallel to the polarization angle.
vectors with the Galactic plane (see the lower panel).
Free-free Emission from Cloud Edges
Free-free (Bremsstrahlung) emission is due to electron-electron scattering from
ionized gas (with T ≈ 104 K) in the ISM. At frequencies higher than 10 GHz, the
free-free thermal emission has a spectrum of T ∼ ν β , with β = -2.15 [2].
The free-free emission is intrinsically unpolarized because of the randomization of
scattering directions. However, at the edges of bright free-free features (i.e. HII regions) a secondary polarization signature can occur as a result of anisotropic Thomson
scattering [25, 52]. This could cause significant polarization (≈ 10%) in the Galactic
plane at high angular resolution. However, at high Galactic latitudes, and with a low
resolution, the residual polarization is expected to be < 1%.
14
1.4.4
Anomalous Dust Emission
There are additional dust emission mechanisms that could produce a low level
of polarized emission. Some studies at high Galactic latitude [53, 54, 55, 56] and
individual Galactic clouds [57, 58], have observed unexpected emission in excess of
that from the three components discussed above (synchrotron, thermal dust, and freefree emission). This emission has been termed “anomalous” for the reason that its
provenance was not completely understood at this time. Some studies [57, 59, 60, 61]
show that this emission is correlated with large-scale maps of far infrared emission
from thermal dust.
There are two main hypotheses for the anomalous emission. The first mechanism
is the spinning dust model: small (≈ 1 nm), rapidly rotating dust grains emit electric
dipole radiation at microwave frequencies [62, 63, 64]. The second is the vibrating magnetic dust model: large (≥ 100 nm), thermally vibrating grains undergoing
fluctuations in their magnetization will emit magnetic dipole radiation at microwave
frequencies [65].
The spinning dust model is favored by some observations [66, 67]. However, emission from vibrating magnetic dust should exist at some level, because large grains are
known to exist from observed emission in the far infrared, and contain ferromagnetic
material [68, 69]. This is important for polarization observations as magnetic dust is
predicted to be better aligned to the magnetic fields than the spinning dust.
The spinning dusts aligned by paramagnetic dissipation [28] emit polarized radiation. Theory predicts the polarization from spinning dust peaks at about 2 GHz
(≈ 7%) and falls below 0.5% above 30 GHz [70]. Observations [71, 72] suggest that
the spinning dust grains are inefficiently aligned and will produce little polarization at
any frequency. There is evidence that the vibrating magnetic grains are well aligned
with the magnetic field. Theory predicts a maximum polarization fraction to be 40%
[65] with the polarization angle flipping within the ∼ 1 - 100 GHz range. The polarization is perpendicular to the magnetic field at higher frequencies, but parallel to
the field at lower frequencies.
15
Chapter 2
Submillimeter Polarimetry of M17
In this chapter, I present the data analysis process of 450 µm polarization observations of the M17 molecular cloud from the Caltech Submillimeter Observatory (CSO)
and discuss the physics of the cloud that we learn from the submillimeter polarimetry.
2.1
Introduction to Submillimter Polarimetry
Although it is possible to measure polarized thermal emission of aligned grains
from mid-IR to millimeter wavelengths [73, 23], for a blackbody spectrum, the peak
of the thermal emission spectrum of a typical molecular cloud (with a temperature
of about 10 K [74]) falls in the submillimeter band (see appendix B). Thus, the
submillimeter waveband is a very important window for studying the physics of these
interstellar medium.
Submillimeter polarimetry provides one of the best methods for mapping interstellar magnetic fields in star forming regions and other interstellar clouds [75]. Magnetic
fields are believed to play an important role in the support and evolution of molecular
clouds via the magnetic flux freezing effect [76].
The way in which polarization data traces the magnetic field is described in section 1.4.2. Basically, the magnetically aligned interstellar dust grains emit partially
polarized thermal radiation. The direction of polarization gives the orientation of the
interstellar magnetic field, as projected onto the plane of the sky (B⊥ ).
16
2.2
Polarimetry at Caltech Submillimeter Observatory
The earliest detections of far-IR/submillimeter polarization in astronomical objects were obtained during the 1980s using single-pixel polarimeters from balloons [77]
and aircraft [78]. In the 1990s, astronomers developed more powerful polarimeters
with tens of pixels, such as Stokes [79] for the Kuiper Airborne Observatory (KAO),
SCU-POL [80, 81] for the James Clerk Maxwell Telescope (JCMT) and Hertz [82] for
the CSO. Since 2006, SHARP [83] has served as a new polarimeter for the CSO.
The CSO is one of the world’s premier submillimeter telescopes on Mauna Kea.
It consists of a 10.4 meter diameter dish with a root-mean-square (rms) surface error
of about 20 µm [84] and an active optics system [85]. The superconductor-insulatorsuperconductor (SIS) receivers [86] of the CSO are available from 180 to 720 GHz
atmospheric windows with the performance close to the theoretical limit given by
“Quantum Noise” [87].
Submillimeter High Angular Resolution Camera II (SHARC II) [88] is a backgroundlimited “CCD-style” bolometer array with 12 × 32 semiconducting bolometric detec-
tors. As a facility camera for the CSO, SHARC II operates at 350 µm and 450 µm
wavebands. In the best 25% of winter nights on Mauna Kea (with τ225 GHz ≈ 0.05),
SHARC II is expected to have a noise equivalent flux density (NEFD 1 ) at 350 µm
of 1 Jy s1/2 or better (equation 2.1 [3] and figure 2.1).
NEFD350 µm = 1.0 × exp(25.0 × τ225 GHz × airmass − 1.6) Jy s1/2 .
(2.1)
SHARP [4] is a foreoptics module that converts the SHARC II camera into a
sensitive dual-beam 12 × 12 pixel imaging polarimeter at wavelengths of 350 and
450 µm. It splits the incident radiation into two orthogonally polarized beams that
are then reimaged onto 12 × 12 subarrays at opposite ends of the 32 ×12 array in
SHARC II. The polarization signal is modulated by a warm rotating half wave plate
(HWP) at front of the polarization-splitting optics.
1
NEFD is defined as the level of flux density required to obtain a unity signal to noise ratio in 1
17
Figure 2.1: NEFD350 µm measurements (points) from Jan 2003 compared to theoretical expectation (solid line) from equation 2.1 [3]. The performance is about 1 Jy s1/2
for τ225 GHz = 0.05.
Figure 2.2 shows the optics of SHARP. The submillimeter light beams from the
focus of the CSO telescope enter SHARP from the left, and are relayed through an
optical path including flat and curved mirrors and polarizing wire grids. The radiation
then passes the M4 mirror and enters the SHARC II camera. The key idea of the
design is to reconstitute the image with an offset between the two orthogonal linear
polarization components. SHARC II can be easily converted back to photometric
mode by removing mirror P1 and F5 in figure 2.2.
The SHARP instrument specification is listed in table 2.1 [89]. With a resolution of
about 5 arc seconds, high sensitivity and low systematic errors, SHARP is a powerful
tool for submillimeter polarimetry.
At present, SHARP and the submillimeter array (SMA) are the only two instruments with submillimeter polarimetric capabilities that are in service. The SMA is
a interferometer consisting of 8 six-meter dishes focusing on high resolution on small
scales. In addition, BLAST-pol, a successor to balloon-borne large-aperture submillimeter telescope (BLAST [90]), has had its first flight over Antarctica, and the data
obtained at 250, 350 and 500 µm are being reduced and analyzed. In the future, the
second of integration with the detector. See secton 4.2.1 for the definitions of NEP, NET and NEQ.
18
Figure 2.2: The polarization splitting optics of SHARP [4] for reconstituting the image
with an offset between the two polarization components. Left: The expanding beam
from the CSO focus is reflected by P1 (paraboloid), F1 (flat mirror), through the HWP
(half wave plate), and reaches the XG (crossed grid), where the polarization radiation
is separated into two orthogonal (horizontal and vertical) components. Right: View
toward the CSO focus. The vertical and horizontal components undergo further
reflections by a series of mirrors and grids, and are displaced laterally at the BC
(beam combiner), before being directed toward SHARC II.
Table 2.1: SHARP Instrument Specifications
λ0 (µm)
350
Bandwidth (∆λ/λ0 )
0.13
FOV (arc sec × arc sec)
55 × 55
Pixel Size (arc sec × arc sec)
4.6 × 4.6
Angular Resolution (arc sec)
9.0
FOV (arc sec × arc sec)
55 × 55
Point Source Flux for (σp = 1%) in 5 Hours (Jy)
3.6
Surface Brightness for (σp = 1%) in 5 Hours (Jy/pixel)
0.63
Max Separation of Main and Reference Beams (arc min)
5.0
Systematic Errors, σp (sys)
< 0.2%
19
450
0.10
55 × 55
4.6 × 4.6
11.0
55 × 55
2.0
0.35
5.0
< 0.2%
R
A
W
H/V
Gain
rgm
Demodula!on
Chopped
C
Data
I
Q
U
Figure 2.3: Flow chart of “SharpInteg”. It starts by masking the raw data file with an
“rgm” file. Then, it demodulates the chopping to calculate the chopped data. After
applying the relative data gain factor between the horizontal and vertical array, it
calculates the I, I-error, Q, Q-error, U and U-error components and saves them into
a new file.
SCUBA-2 [91] instrument being commissioned at the JCMT also has a polarimeter,
POL-2, and the ALMA interferometer should also have polarimetric capabilities at
multiple submillimeter/millimeter wavelengths.
2.3
SHARP Data Pipeline
There are two data processing programs for SHARP pipeline: “SharpInteg” and
“Sharpcombine”. “SharpInteg” is a program that takes a cycle of half wave plate measurement from SHARP and process it to for I, Q and U along with the corresponding
errors. “Sharpcombine” is for map combining and smoothing.
As shown in figure 2.3, “SharpInteg” first reads in the SHARC II raw data file and
apply a pixel mask to it from a pixel mask file (“rgm” file). After that, the chopping is
demodulated, and the data at different chop/nod positions is given a weight equals to
the number of samples at that position. The chopped data is calculated by summing
the weighted raw data within each sampling period. In the next step, the relative data
20
I
Q
U
I
Q
U
B
S
I
Q
U
I.P.
S
I
Q
U
I
Q
U
I
Q
U
B
S
I
Q
U
I.P.
S
I
Q
U
Rot
I
Q
U
Rot
I
Q
U
I
Q
U
I
Q
U
I
Q
U
B
S
I
Q
U
I.P.
S
I
Q
U
Rot
I
Q
U
Figure 2.4: Flow chart of “Sharpcombine”. It applies τ and telescope pointing correction, background subtraction (BS), instrument polarization (I.P.) subtraction and
polarization angle rotation to sky coordinates (Rot) to each sub-map before it combines them into a large map and smooths it.
gain factor (f) between the horizontal (“H”) and vertical (“V”) array is calculated by
taking all of the samples from a particular HWP position and fitting to the line of “V
= a H + b” using numerical method. After this is done for all HWP positions, the
median value is taken and f is set to the inverse value of the median. The “H” and
“V” array samples are combined after calculating the f value. Finally, The I, I-error,
Q, Q-error, U and U-error maps are calculated and saved to a FITS file.
“Sharpcombine” starts with the output FITS files from “SharpInteg” containing
the I, Q and U map. Each of them represents a small map to be combined to a large
map. In the first step, it applies τ (atmospheric optical depth) and telescope pointing
21
Figure 2.5: M17 is a premier example of a young, massive star formation region in
the Galaxy. Left: A M17 image from my 80 mm aperture optical telescope. Right:
A false color image from Spitzer GLIMPSE (red: 5.8 um; green: 4.5 um; blue: 3.6
um.) [5].
corrections to the small maps. After that, it applies background subtraction (BS)
to I, Q and U data, and instrument polarization (I.P.) subtraction to the Q and U
data in each map. All the maps are rotated to the sky direction (Rot) before being
combined to a big map. Finally, the I, Q and U maps are combined to a large map
and smoothed by interpolation (see figure 2.4).
2.4
Introduction to M17
M17, the Omega Nebula, locating at the constellation Sagittarius with (l, b) =
(15.05, -0.67), is a premier example of a young, massive star formation region in the
Galaxy. It is one of the brightest IR and thermal radio sources in the sky. The
distance of the M17 is measured to be 1.6 ± 0.3 kpc [92]. It covers an area of about
11 arc min × 9 arc min across the sky (figure 2.5).
A global shell structure geometric model of M17 is presented by [6]. In the in-
ner part of the nebula, a bright, photoionized region with a hollow conical shape
surrounds a central star cluster. This region is about 2 pc across and expanding
westward into the outer molecular cloud. There is a large, unobscured optical HII
region spreading into the low density medium at the eastern edge of the molecular
22
cloud. Gas photoexcited by the early OB stars is concentrated in the northern and
southern bars.
X-ray observations [93, 94] indicate that the region interior to the HII region is
filled by hot (106 - 107 K) gas, which is flowing out to the east. [93] noted that this
region is too young to have produced a supernova remnant and interpret the X-ray
emission as hot gas filling a super bubble blown by the OB star winds. In the middle
of the nebula, velocity studies show an ionized shell with a diameter of about 6 pc.
On the western side of the outer part, all tracers of warm and hot gas are truncated
by a wall of dense, cold molecular material which includes the dense cores known
as “M17 Southwest” and “M17 North”, which exhibit many other tracers of current
massive star formation. At this region, Only the most massive members of the young
NGC6618 stellar cluster [95] exciting the nebula have been characterized, due to the
comparatively high extinction.
Figure 2.6 shows a simple M17 model. We can represent the system as a central
cluster of stars surrounded by successive layers of H+ , H0 , and H2 gas to the SW side
and by a background sheet of ionized and neutral gas wrapping around to the NE.
2.5
2.5.1
M17 Polarimetry Results
General Results
Our M17 map from the SHARP 450 µm observation, is centered at 18h 17m 32.0s ,
−16◦ 14′ 25.0′′ (B1950) or 18h 20m 25.2s , −16◦ 13′ 02.1′′ (J2000). It covers an area of
about 4′ 25′′ × 2′ 45′′ at the SW bar of M17 (figure 2.10). Taking the distance to M17
to be about 1.6 kpc (section 2.4), our map coverage is equivalent to an area of 2.05
pc × 1.28 pc.
M17 polarization vectors are plotted in figure 2.7 and a table of the vectors is
listed in appendix A.5. As we can see in figure 2.7, for regions of high submillimeter
flux, the average polarization fraction is lower than that in low flux regions. This is
caused by the line of sight (LOS) effect: assuming the polarization angles at different
distances along the los to be variable, the measured polarization fraction trends to
23
Figure 2.6: A M17 model from [6]. The system can be described as a central cluster
of stars surrounded by successive layers of H+ , H0 , and H2 gas, that expanding with
different velocities to the outer side of the cloud.
become diluted upon integration along the LOS.
The magnetic field projected onto the plane of the sky can be approximated by
rotating the polarization vectors by 90◦ (section 1.4.2). Our results for the magnetic
field direction are in good agreement with the those of previous observations at far-IR
(Stokes, 60 and 100 µm) [7, 23] and submillimeter (Hertz, 350 µm) [24] wavebands,
but with much higher resolution (figure 2.10).
Figure 2.8 shows the distribution of polarization fraction of the measurements.
The average polarization fraction is about 2.4%, a typical number for magnetically
aligned molecular clouds. The mean polarization angle (from north to east) is about
−5.0◦ (figure 2.9), which gives an average magnetic field almost parallel to the RA
direction.
Figure 2.10 shows the magnetic field distribution from 100 um [7], 450 um (SHARP)
and optical observations [8]. The 8.00 µm Spitzer GLIMPSE flux map are mostly
due to the polycyclic aromatic hydrocarbons (PAHs) molecular emission.
The magnetic field follows the molecular cloud and the curvature of the HII region.
24
Figure 2.7: M17 polarization fraction vectors are plotted over the 450 um uncalibrated
flux map. Thick vectors are detected with greater than or equal to 3σ level and thin
vectors are between 2σ and 3σ level. The circle on the bottom right shows the SHARP
beamsize. Some parts of the flux map is removed due to high noise levels. Offsets are
from 18h 17m 32s , -16◦14′ 25′′ (B1950.0).
25
Median = 1.90, Mean = 2.36, Std = 1.81
80
70
60
Number
50
40
30
20
10
00 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Polarization (%)
Figure 2.8: Histogram of M17 polarization fraction. This distribution includes all
vectors at greater or equal to than 2σ level. All vectors greater than 10% are 2σ
vectors.
40
Median = -4.00, Mean = -5.02, Std = 30.39
35
30
Number
25
20
15
10
5
0 90 80 70 60 50 40 30 20 10 0 10 20 30 40 50 60 70 80
Polarization Angle (degree)
Figure 2.9: Histogram of M17 polarization angle. Polarization angles are measured
from north to east. The resulting net magnetic field is almost parallel to the RA
direction.
26
The center OB type stars heat the HII region and carve a hollow conical shape into
the molecular cloud and separating it into two parts: the M17 SW and the M17 N.
It is found that PAHs are destroyed over a short distance at the photodissociation
region (PDR) around the edge of the HII bubble [5].
2.5.2
Polarization Spectrum
There are several instruments that contribute multiwavelength polarimetric data
from far-IR (Stokes) to submillimeter (Hertz, SHARP, SCU-POL). If the source of
the polarized emission is a single population of dust grains with similar polarization properties and temperature, then one expects the magnitude of the polarization
(polarization fraction) to be nearly independent of wavelength higher than 50 µm
[96, 97].
The far-IR to submillimeter polarization spectrum of various molecular clouds
have been studied by observations [97, 98, 99, 100] and simulations [101, 102]. The
polarization spectrum of M17 at 60 um (Stokes, 22′′ resolution), 100 um (Stokes, 35′′
resolution) and 350 um (Hertz, 20′′ resolution) had been studied by [97, 98] and their
results are shown in figure 2.12. It has been found that the spectra are falling from
far-IR to about 350 µm and rising towards longer wavelengths.
The analysis presented here incorporate the 450 µm SHARP polarimetric data
(about 10′′ resolution). The polarization data points that are to be compared between
two wavelengths are chosen based on the following criteria [97]: (1) The vectors are in
the same region of the same cloud; (2) The difference between the polarization angle
must be within 10◦ ; (3) The vectors are from the cloud envelope; (4) All vectors are
greater or equal to 3σ level.
Applying the above criterion, the surviving vectors at 60 µm to 450 µm are plotted
in figure 2.11. They share a common area (marked by a green shadow) between
18h 17m 30s and 18h 17m 37s in Ra (B1950), −16◦ 16′ 20′′ and −16◦ 13′ 00′′ in Dec (B1950).
A summary of the result is presented in table 2.2 and the details can be found
in appendix A. The M17 polarization spectrum from 60 µm to 450 µm is plotted
in figure 2.12. Our basic result is P450 < P350 < P100 < P60 . In contrast to the
27
Figure 2.10: Magnetic field vectors from SHARP (red, 450 um), Stokes (green,100 um)
[7] and optical observation [8] (purple) plotted on top of Spitzer GLIMPSE 8.00 um
flux map. The magnetic vectors from SHARP and Stokes are perpendicular to their
polarization angles, while those from optical polarization measurement are parallel
to their polarization angles. All magnetic vectors (plotted with the same length) are
used to indicate the direction only. Offsets are from 18h 17m 32s , -16◦ 14′ 25′′ (B1950.0).
28
Figure 2.11: The common area (green shadow) for polarization spectrum analysis. It
is between 18h 17m 30s and 18h 17m 37s in Ra (B1950), −16◦ 16′ 20′′ and −16◦ 13′ 00′′ in
Dec (B1950). The selected polarization vectors are at 60 µm (yellow), 100 µm (green),
350 µm (blue) and 450 µm (red). Background is the 450 µm flux map. Offsets are
from 18h 17m 32s , -16◦14′ 25′′ (B1950.0).
29
Ratio
P450 /P60
P450 /P100
P450 /P350
Table 2.2: M17 Polarization Spectrum Data
Points Median Mean Std
Note
13
0.390
0.395 0.056 see appendix A.1 for details
11
0.520
0.525 0.128 see appendix A.2 for details
22
0.795
0.887 0.289 see appendix A.3 for details
results from other clouds, our work shows that, in the common area, the M17 has
lower median polarization at 450 µm than at 350 µm. The polarization spectrum
falls monotonically from 60 µm to 450 µm.
There are many models to explain the rising (or falling) of the polarization spectrum from far-IR to submillimeter wavelength. Generally speaking, the radiation
environment plays an important role in forming the polarization spectrum, since the
grain alignment efficiency is dependent on radiative torques (section 1.4.2). In a weak
radiation field, the polarization spectrum normally has a positive slope (towards long
wavelengths) [101]. That is what we observed from many clouds from 350 µm to 450
µm (figure 2.12). Our result of a negative slope (P450 < P350 ) from the east part of
the cloud indicates the existence of a strong radiation field from that direction.
2.5.3
Spatial Distribution of Magnetic Field and Polarization
Spectrum
As already shown in figure 2.10, the center OB type stars in M17 heat the HII
region and carve a hollow conical shape into the molecular cloud. Our analysis shows
that this shock front is passing through our sampled region. Figure 2.13 shows 450
µm magnetic vectors plotted over the [21 cm]/[450 µm] ratio map (with the peak
normalized to 1.0). The shock is following the “-Y” direction. We can separate the
cloud into three regions: “post-shocked”, “shock front” and “pre-shocked” by the “y
= 0” and “y = -50 arcsec” lines.
The “post-shocked” region has consistent polarization angles with an average of
about 18◦ ; in the “shock front” region, where the magnetic field is being distorted, the
30
4
W51
M17
OMC−1
NGC2024
DR21
OMC−3
This work
Median Polarization Ratio
3
2
1
40
100
200
400
Wavelength (um)
1000
2000
Figure 2.12: Polarization spectrum of some popular interstellar molecular clouds [9].
The median polarization ratio are normalize by the value at 350 µm. In contrast to the
results from other clouds, our work shows that, the M17 has lower median polarization
at 450 µm than at 350 µm. The polarization spectrum falls monotonically from 60
µm to 450 µm.
31
polarization angle distribution spreads out in a large range from -40◦ to 60◦ and the
polarization fractions become small; in the “pre-shocked” region, polarization angles
become consistent again and the polarization fraction is much higher before being
destroyed by the shock. The distributions described above are shown in figure 2.14
and 2.15, which show that the polarization angles and fractions are correlated with
the “Y” axis in a linear and a “U” shape relationship.
In the dense region of the cloud, the magnetic fields survive the windswept of the
shock. There is an example in figure 2.13 (see the region marked by a blue box). The
magnetic field in the dense cloud is different from other vectors in the “post-shocked”
region. This cloud core can also be seen in figure 2.7, 2.10 and 2.11.
Figure 2.16 shows the magnetic field vectors (red) and intensity contours of SHARP
(green, levels = {0.0, 0.2, 0.4, 0.6, 0.8, 1.0}) over plotted on the 21 cm absorption-line
contour and the ratio of neutral HI (NHI) column density to the spin temperature
Tspin distribution map in the 17.5-22 km/s velocity area from [6]. The expanding
HI region (see figure 2.6) is corresponding to the “post-shocked” and part of “shock
front” region. The NHI/Tspin density is low at the dense cloud region (see figure 2.13),
which is still dominated by the H2 molecular cloud.
One conclusion from the above discussion on the polarization spectrum is at the
common region, P450 is smaller than P350 . But in other parts of the cloud, we found
that P450 is greater than P350 (figure A.3 and appendix A.4). In figure 2.17, the [450
µm]/[350 µm] polarization ratio vectors are over plotted on the [21 cm]/[M17 450um]
flux ratio map. As we can see, most of the blue vectors are within the common region
defined in figure 2.11. In spite of some red vectors distributed round the dense cloud
region, the contour line with the [21 cm]/[450 µm] = 0.1 separates the blue and red
vectors into two regions. Figure 2.18 also agrees with this conclusion: the blue vectors
are mostly related to the east “post-shocked” region, where the star radiation field is
strong, while the red vectors are related to the molecular region with weak radiation
fields.
32
Dec
y = 0 y = -50
Y
Dense Cloud
Ra
66.3
o
X
Figure 2.13: Magnetic vectors from SHARP plotted over the [21 cm]/[450 µm] flux
ratio map, showing that the shock front is passing through the cloud. The contour
levels are {0.1, 0.3, 0.5, 0.7, 0.9}. The “X” axis is defined by fitting contour level
= 0.1. The new “X-Y” coordinate system is about 66.3◦ with respect to the “RaDec” coordinates. The shock is following the “-Y” direction. The “y=0” and “y=-50
arcsec” lines separate the cloud into “post-shocked” (y > 0), “shock front” (-50 < y <
0) and “pre-shocked” (y < -50) regions. The polarization directions and magnitudes
in these regions are different (figure 2.14 and 2.15). The magnetic fields in the dense
cloud (can also be seen in figure 2.10) at the top of the map survive the windswept.
Offsets are from 18h 17m 32s , -16◦14′ 25′′ (B1950.0).
33
100
80
60
60um
100um
350um
450um
(degree)
40
20
0
20
40
60
80
150
100
0
50
Y (arcsec)
50
100
Figure 2.14: Correlation between polarization angle and the Y direction (zero at
18h 17m 32s , −16◦ 14′ 25′′ ), showing a linear relationship. The “post-shocked” region is
at y > 0 and the “pre-shocked” region is at y < −50 arcsec.
12
60um
100um
350um
450um
10
p (%)
8
6
4
2
0150
100
0
50
Y (arcsec)
50
100
Figure 2.15: Correlation between polarization fraction and Y direction (zero at
18h 17m 32s , −16◦ 14′ 25′′ ), showing a “U” like shape. The polarization fraction is higher
at the “post-shocked” region at y > 0 and the “pre-shocked” region at y < −50 arcsec.
34
Figure 2.16: Magnetic field vectors (red) and intensity contours of SHARP (green,
levels = {0.0, 0.2, 0.4, 0.6, 0.8, 1.0}) are over plotted on the 21 cm absorption-line
contour and the ratio of neutral HI (NHI) column density to the spin temperature
Tspin distribution map in the 17.5-22 km/s velocity area from [6]. This velocity
component is correlated with the “post-shocked” and part of “shock front” region.
The NHI/Tspin density at the dense cloud region (see figure 2.13) is low.
35
Figure 2.17: The [450 µm]/[350 µm] polarization ratio vectors over plotted on the
[21 cm]/[450 µm] flux ratio map with contour levels = {0.1, 0.3, 0.5, 0.7, 0.9}. The
blue (red) vectors represent P450 < (>) P350 . The length of the 2% bar at bottom left
is equivalent to P450 /P350 = 1.0. The directions of the vectors are parallel to their
polarization angles. Offsets are from 18h 17m 32s , -16◦ 14′ 25′′ (B1950.0).
36
Figure 2.18: The [450 µm]/[350 µm] polarization ratio vectors and 450 µm intensity
contours of SHARP (green, levels = {0.0, 0.2, 0.4, 0.6, 0.8, 1.0}) over plotted on the
Fig.1 from [7]. The blue vectors is found to be correlated with the [OI] line, which is
a tracer for the atomic gas.
37
2.5.4
Conclusion
The combination of multi wavelength study and the polarimetric data from far-IR
to submillimeter reveal the violent physical process in the M17 cloud.
At large scale, the young OB type stars in the center of the cloud heat the HII
region up to 106 - 107 K and create a high energy fountain towards the southeast
direction. The HII wind push the HI and H2 regions outwards, creating a hollow
conical shape into the cloud. The magnetic field is found following the curve of the
HII region.
On small scales, within our field of view, the shock is passing through the boundary
between the HI and H2 region. There are significant differences between the dust
alignment before and after the shock. The polarization properties and temperature
of the dust population are also changed by the wind. Our study also shows that a high
density molecular clump is being blasted by the out-going wind, while the magnetic
field distribution in the area remains unchanged.
It is the first time to observe the variance of polarization ratios across a molecular
cloud. There are still no models that can explain this result. One conclusion we can
make is that the grains in the cloud are not always aligned with the magnetic field
perfectly, and any model trying to explain the polarization spectrum should take into
account the variance of interstellar physical condition along the line of sight.
38
Part II
Polarimetry in Cosmology
39
Chapter 3
Introduction to Polarization in
Cosmology
3.1
The Big Bang Theory
The Big Bang theory describes the evolution of our universe. It posits that our
universe started from a hot and dense phase about 13.75 billion years [14] ago and
the content of the universe kept evolving after that. In inflation theory, the universe
was dominated by an energy field with a negative pressure, which drove an early
period of accelerated expansion. It was then dominated by radiation, and later by
matter. And now, it has again become dominated by a dark energy that is driving a
slower accelerated expansion (equation 3.27). The term “Big Bang” was first coined
by Fred Hoyle, when he was trying to belittle the credibility of the theory. However,
The Big Bang has became the standard cosmological framework for understanding
the universe and is supported by many lines of evidence.
3.1.1
The Expanding Universe–Hubble’s Law
In 1929, Edwin Hubble announced his discovery (now Hubble’s Law) [103], that
describes the relation between radial velocity (V ) and distance (D) of extra-Galactic
40
“nebulae” (galaxies):
V = H0 D
(3.1)
where H0 is Hubble constant.
Hubble’s law basically describes that the more distant the galaxy, the faster it is
receding from us and galaxies are moving away from each other. It is the result that
we expect for a uniformly expanding universe.
3.1.2
Big Bang Nucleosynthesis (BBN)
At the time of about 3 minutes after the Big Bang, the universe is hot and dense.
There were no atomic elements, but rather a sea of neutrons, protons, electrons,
positrons, photons and neutrinos. As the universe cooled, the following processes
occurred:
n → p+ + e− + ν̄e
n + p+ →21 D + γ
2
1D
+ p+ →32 He + γ
2
1D
+21 D →42 He + γ
2
1D
+21 D →31 T + p+
2
1D
+31 T →42 He + n
... ...
(3.2)
This process of light element formation in the early universe is called “Big Bang
nucleosynthesis” (BBN). It lasted for only about 17 minutes. After that, the limited
lifetime of free neutrons ended the process, while the temperature and density of
the universe fell below that which is required for nuclear fusion. The brevity of
BBN is important because it predicts that only light elements could be form, and
the abundance of light elements are: Hydrogen(1 H) ≈ 75%, Helium(4 He) ≈ 25%,
Deuterium(2 H) ≈ 0.01%, Helium(3 H) ≈ 0.001%, Lithium(7 Li) ≈ 10−10 [104, 105].
This prediction is in agreement with observations.
In 2011, pristine clouds of the primordial gas were found [106]. These clouds of gas
was discovered by analysing the light from distant quasars. Absorption lines that can
be used to measure the composition of the gas appeared in the spectrum where the
41
light was absorbed by the gas. The composition of the gas matches the predictions
from BBN, providing the latest direct evidence in support of the modern cosmological
explanation for the origins of elements in the universe.
3.1.3
The Cosmic Microwave Background (CMB) Radiation
The CMB radiation was predicted as radiation left over from an early stage in the
development of the universe (section 3.4), and its discovery is considered a landmark
success of the Big Bang theory, ruling out the competing Steady State Theory [107].
In 1964, Arno Penzias and Robert Wilson discovered the cosmic background radiation while conducting diagnostic observations using a microwave receiver [108]. Their
discovery confirmed the CMB predictions from the Big Bang theory–an isotropic and
consistent blackbody spectrum with a temperature of about 3 K.
The Cosmic Background Explorer (COBE) satellite was launched in 1989. Its
findings were consistent with the Big Bang’s predictions regarding the CMB. COBE
found a precise blackbody spectrum (reflecting thermal equilibrium between matter
and radiation in the early universe) with a temperature of 2.725±0.001 K and detected
for the first time the fluctuations (anisotropy) in the CMB, at a level of about one
part in 105 [109].
In early 2003, the first results of the Wilkinson Microwave Anisotropy Probe
(WMAP) were released [11]. These results tested and refined a standard cosmological
model with accurate values for the cosmological parameters. The WMAP results were
also consistent with the inflation theory.
A new generation space probe – the Planck satellite, was launched in 2009. It has
goals similar to WMAP –to provide even more accurate measurements of the CMB
anisotropy while further testing the model. There are also many other ground- and
balloon-based experiments targeting various aspects of the CMB.
3.1.4
Other Evidence
Observations of the morphology and distribution of galaxies and quasars also
provide strong evidence for the standard model of cosmology. Observations suggest
42
that the first quasars and galaxies formed when the age of the universe was only about
0.5 billion years and distant galaxies (galaxies formed in the early universe) appear
very different from nearby galaxies (galaxies formed recently). These observations
agree well with numerical simulations [110]. The age of universe determined to < 1%
from the CMB is also in good agreement with other estimations, i.e. using the ages
of the oldest stars.
3.2
Cosmic Inflation
Cosmic inflation was originally proposed by Alan Guth [111, 112], Alexei Starobinsky [113], Andrei Linde [114], Andreas Albrecht and Paul Steinhardt [115]. It posits
that there was a rapid exponential expansion of the early universe by a factor of at
least 1078 in volume, driven by a negative pressure energy (ω < −1/3). Following
the grand unification epoch (between 10−43 s and 10−36 s after the Big Bang), the
inflationary epoch comprises the first part of the electroweak epoch (between 10−36 s
and 10−12 s after the Big Bang). It lasted from 10−36 s to about 10−32 s. After that,
the universe continued to expand at a rate that was much slower than inflation.
While the detailed physics mechanism responsible for inflation is still unknown,
inflation makes a number of predictions that have been confirmed by observations,
such as CMB observations, galaxy surveys and 21 cm radiation observations. Inflation
is thus now considered to be an extension of the Big Bang theory. It resolves several
problems in the Big Bang cosmology.
3.2.1
The Structure Problem
Considerable structures in the universe, from stars to galaxies to clusters and
super clusters of galaxies have been observed. How did these structures form? The
Big Bang theory does not account for the needed fluctuations to produce the structure
we see. Inflation gives a solution to this problem: Quantum fluctuations in the
nearly-uniform density of the early universe expanded to cosmic scales during cosmic
inflation. These fluctuations also would have left an imprint in the CMB radiation
43
in the form of temperature fluctuations from point to point across the sky (the CMB
anisotropy). The structures that we observe today grew from the gravitational pull
of these fluctuations.
3.2.2
The Flatness Problem
Observations show that the geometry of the current universe is nearly flat (section 3.3.3). However, under the nominal Big Bang theory, curvature grows with time.
A universe as flat as we see it today would require an extreme fine-tuning of conditions
in the past, which would be an unbelievable coincidence. Inflation provides a solution to this problem via the stretching of any initial curvature of the 3-dimensional
universe to near flatness, resulting Ωk ≈ 0.
3.2.3
The Horizon Problem
The uniformity of the CMB temperature (section 3.4) implies that the entire
observable universe must have been in causal contact in the past. But now the
distance between two regions with ≥ 2◦ apart in the sky are so far apart that, they
could never have been in causal contact with each other, because the light travel
time between them is greater than the age of the universe. This can be explained by
inflation theory: Distant regions were actually much closer together prior to inflation
than they would have been with only standard Big Bang expansion. Thus, such
regions could have been in causal contact prior to inflation and could have attained
a uniform temperature.
3.2.4
The Magnetic Monopole Problem
The Big Bang theory predicts that the early universe produced a very large number of heavy and stable magnetic monopoles. However, these magnetic monopoles
have never been observed so far. The explanation from inflation is that, during inflation, the density of monopoles drops exponentially, so their abundance drops to
undetectable levels.
44
3.3
ΛCDM Cosmological Model
The Λ Cold Dark Matter (ΛCDM) model is a model of the content of the universe that includes baryons, cold dark matter, photons, neutrinos and a cosmological
constant Λ.
3.3.1
Cosmological Principles and FLRW metric
The cosmological principle is that, on sufficiently large scales, the universe is homogeneous and isotropic. Homogeneity implies translational invariance and isotropy
implies rotational invariance. These principles are distinct but closely related, because
a universe that appears isotropic from any two locations must also be homogeneous.
The isotropic principle is supported by the observations: (1) Radio galaxies are
randomly distributed across the sky; (2) The large scale distribution of galaxies is
isotropic in the range of greater than 200 Mpc; (3) The observed redshift distribution
of distant galaxies is isotropic, which implies a uniform expansion of space in all
directions; (4) The Cosmic Microwave Background (CMB) radiation is constant in
all directions to within 1 part in 105 (section 3.1.3).
A universe must be non-static if it follows the cosmological principle. In 1923,
Alexander Friedmann derived a version of Einstein’s equations of general relativity
describing the dynamics of a homogeneous and isotropic universe. After that, Georges
Lemaı̂tre, Howard P. Robertson and Arthur G. Walker also derived the general relativity metric for the cosmological principle independently. It is named Friedmann Lemaı̂tre - Robertson - Walker (FLRW) metric.
In the four space-time dimensions, using Einstein notation, the invariant is:
ds2 = gµν dxµ dxν
where the µ and ν indices range from 0 to 3.
The FLRW metric can be written as:
45
(3.3)
gµν
and its inverse is:

−1

0

=
0

0
g µν

0
0
0
a2
1−kr 2
0
0
0
a2 r 2
0
0
0
a2 r 2 sin2 θ

−1

0

=
0

0
0
0
0
1−kr 2
a2
0
0
0
1
a2 r 2
0
0
0
1
a2 r 2 sin2 θ













(3.4)
(3.5)
where a = a(t) is the time-dependent cosmic scale factor and k is a constant representing the curvature of the space.
µ
The Riemann curvature tensor Rαβγ
is defined by:
µ
Rαβγ
dΓµαβ
dΓµαγ
−
+ Γµσβ Γσγα − Γµσγ Γσβα
=
dxβ
dxγ
where Γ are the Christoffel symbols:
∂gµλ
1 αν ∂gµν ∂gλν
α
+
−
.
Γλµ = g
2
∂xλ
∂xµ
∂xν
(3.6)
(3.7)
Also, the Ricci tensor Rµν is defined as:
α
Rµν = Rµνα
.
(3.8)
The diagonal elements of the Ricci tensor are:
ä
a
aä + 2ȧ2 + 2k
=
1 − kr 2
R00 = −3
R11
R22 = r 2 (aä + aȧ2 + 2k)
R22 = r 2 (aä + aȧ2 + 2k)sin2 θ
(3.9)
and the trace of the Ricci tensor is the scalar curvature R:
R ≡ g µν Rµν = 6
46
aä + ȧ2 + k
.
a2
(3.10)
3.3.2
Einstein Field Equations and Friedmann Equation
The Einstein Field Equations (EFEs), that are used to determine the spacetime
geometry resulting from the presence of mass-energy and momentum, can be written
in the form of:
1
Rµν − gµν R + gµν Λ = 8πGTµν
(3.11)
2
where Λ is the cosmological constant, G is the gravitational constant and Tµν is the
energy-momentum tensor.
For perfect isotropic fluid in equilibrium, Tµν can be written as:
Tµν = (p + ρ)uµ uν + pgµν
(3.12)
where ρ is density, p is pressure and uµ is the four velocity.
By plugging equation 3.8, equation 3.9, equation 3.10 and equation 3.12 into
equation 3.11, we have:
2
ȧ
Λ
8πG
k
H ≡
=
ρ− 2 +
a
3
a
3
2
and
(3.13)
4πG
Λ
ä
=−
(ρ + 3p) +
(3.14)
a
3
3
where H is the Hubble parameter that gives the rate of expansion of the universe
and k is the curvature constant that belongs to the set of {-1, 0, +1}, standing for a
{negative, zero, positive} curvature.
Equation 3.13 is the Friedmann equation, which describes the expansion of a ho-
mogeneous and isotropic universe within the context of general relativity. The Hubble
constant is the current value of Hubble parameter H0 = H|t=t0 = 100h km s−1 Mpc−1 =
70.4 km s−1 Mpc−1 [14], where h = H0 /(100 km s−1 Mpc−1 ) = 0.704. Equation 3.14
is the acceleration equation, describing the accelerated expansion rate of the universe.
Λ can be absorbed into ρ and p, by replacing ρ + ρΛ → ρ and p − pΛ → p, where
ρΛ = Λ/(8πG) and pΛ = Λ/(8πG). Equation 3.13 and equation 3.14 can be simplified
as:
2
8πG
k
ȧ
=
ρ− 2
a
3
a
47
(3.15)
and
ä
4πG
=−
(ρ + 3p).
a
3
(3.16)
For a perfect isotropic fluid, from the first law of thermodynamics dE + P dV = 0,
one can derive the fluid equation of the universe:
ȧ
ǫ̇ + 3 (ǫ + p) = 0,
a
(3.17)
where ǫ = ρc2 is the energy density.
We can define the equation of state as:
p = ωǫ
(3.18)
where the dimensionless number ω is the equation of state parameter.
From equation 3.15, equation 3.16, equation 3.17 and equation 3.18, we have:
ȧ2 =
and
k
8πG X
ǫω,0 a−1−3ω − 2
3 ω
a
(3.19)
ä
4πG
=−
(1 + 3ω)ǫ.
a
3
(3.20)
where ǫω,0 is the energy density of the species with equation of state parameter ω.
For a flat universe, k = 0. From the above equations, we can derive:
ρ ∝ a−3(ω+1)
(3.21)
and
2
a ∝ t 3(ω+1) .
(3.22)
Different species in the universe have different equation of state parameters: (1)
1
For photons and other relativistic species, ω = 1/3, ρ ∝ a−4 and a ∝ t 2 ; (2) For
2
non-relativistic matter (cold dark matter and baryons), ω = 0, ρ ∝ a−3 and a ∝ t 3 ;
(3) For dark energy, ω < −1/3 and ä > 0. Dark energy accelerates the expansion
of the universe. (4) For Λ, ω = −1, ρ ∝ a0 = constant and a ∝ exp(H0 t). The
cosmological constant represents a special kind of dark energy.
48
The total density of the universe, Ω0 , is defined as the ratio of the actual (observed)
density ρ0 to the critical density ρc,0 of the Friedmann universe:
3H02
8πG
8πGρ0
=
.
3H02
ρc,0 =
ρ0
ρc,0
If we introduce a new set of definition:
Ω0 =
Ωr,0 ≡
ǫm,0
ǫΛ,0
ǫr,0
, Ωm,0 ≡
, ΩΛ,0 ≡
ǫc,0
ǫc,0
ǫc,0
(3.23)
(3.24)
(3.25)
and
Ω0 = Ωr,0 + Ωm,0 + ΩΛ,0
Ωk = 1 − Ω0
(3.26)
where ǫc,0 = ρc,0 c2 , indices r, m, Λ and k stand for radiation, matter, cosmological
constant (dark energy) and curvature, respectively. Equation 3.15 can be written as:
H 2 (t)
Ωr,0 Ωm,0
Ωk
= 4 + 3 + ΩΛ,0 + 2 .
2
H0
a
a
a
(3.27)
The last term on the right hand side is related to curvature. In a flat universe,
Ω0 = 1, Ωk = 0. Equation 3.27 describes the evolution of the universe with a
combination of different species: After inflation (section 3.2), which was dominated
by a negative pressure, when a ≪ 1, the universe was dominated by radiation (∝ a−4 ),
and later by matter (∝ a−3 ). Now, at a = 1, it has again become dominated by a
negative pressure energy (dark energy) that is driving an accelerated expansion.
3.3.3
Best-fit ΛCDM Model Parameters
The ΛCDM model currently has six parameters: baryon density (Ωb ), dark matter
density (Ωc ), dark energy density (ΩΛ ), scalar spectral index of spatial fluctuation
(ns ), curvature fluctuation amplitude (∆2R ) and reionization optical depth (τ ). Other
model values, including the Hubble constant and age of the universe, can be derived
from these parameters. Table 3.1 lists the best-fit parameters of the ΛCDM model
[14] based on data from Wilkinson Microwave Anisotropy Probe (WMAP), Baryon
Acoustic Oscillations (BAO) and Hubble constant (H0 ) measurements.
49
Table 3.1: Best-fit ΛCDM Model Parameters
Basic parameter
Value
Description
Ωb
0.0456 ± 0.0016
Baryon density
Ωc
0.227 ± 0.014
Cold dark matter density
ΩΛ
0.728+0.015
Dark energy density
−0.016
ns
0.963 ± 0.012
Scalar spectral index
−1
+0.088
2
−9
∆R (k0 = 0.002Mpc ) (2.441−0.092 ) × 10
Curvature fluctuation amplitude
τ
0.087 ± 0.014
Reionization optical depth
Extended parameter
Value
Description
+1.3
H0
70.4−1.4
Hubble constant (km s−1 Mpc−1 )
t0
13.75 ± 0.11
Age of the universe (Gyr)
r
< 0.24(95% CL)
Tensor-to-scalar ratio
+0.0056
Total density
Ω0
1.0023−0.0054
Ωk
−0.0023+0.0054
Curvature
density
−0.0056
+0.68
z∗
1090.89−0.69
Redshift at decoupling
t∗
377730+3205
Age
at decoupling (yr)
−3200
zreion
10.4 ± 1.2
Redshift of reionization
The universe is nearly flat
If the density of the universe, ρ0 , is greater than critical density, ρc,0 , then Ω0 > 1.0,
Ωk < 0, the geometry of space is closed. In this space, initially parallel photon paths
converge and return back to their starting point; If ρ0 < ρc,0 , Ωk > 0, then the
geometry of space is open and negatively curved like the surface of a saddle; From
+0.0054
table 3.1, we have Ω0 = 1.0023+0.0056
−0.0054 , Ωk = −0.0023−0.0056 . These measurements
show that the geometry of the universe is within measurement error of a flat space.
If flat or negatively curved, it is infinite in extent, unless the cosmological principle
does not hold on scales much greater than the horizon scale.
A solution to the flatness problem is given by the inflation theory (section 3.2).
It proposes a period of extremely rapid (a factor of ∼ 1026 in scale in only a small
fraction of a second) expansion of the universe prior to the more gradual Big Bang
expansion. Inflation stretches the geometry of the universe towards flatness.
50
Relativistic species in the universe
The main relativistic species are the Cosmic Microwave Background (CMB) photons (see section 3.4) and neutrinos. The energy density of photon can be calculated
by Bose-Einstein distribution:
ρ=g
Z
d3 p
f (~x, ~p)E(p),
(2π)3
(3.28)
where, ρ is the energy density, g is the degeneracy, f (~x, p~) is the distribution function,
and E(p) = (p2 + m2 )1/2 is the energy at a given stage p.
For photons, g = 2, f (~x, p~) = 1/(eE(p)/Tγ − 1) and E(p) = (p2 + m2 )1/2 = p, thus
(note that d3 p = 4πp2 dp):
p
d3 p
3
p/T
(2π) e γ − 1
Z ∞
8π
p3
=
dp
(2π)3 0 ep/Tγ − 1
π2 4
= Tγ
15
ργ = 2
Z
(3.29)
So,
ργ,0
π2 4 1
π 2 4 8πG
= Tγ,0
= Tγ,0
ρc,0
15
ρc,0
15
3H02
π 2 4 −2
= Tγ,0
h × 6.808 × 10−7 = 4.98 × 10−5
15
Ωγ,0 =
(3.30)
where Tγ,0 = 2.725 K is the temperature of the CMB measured today and h = 0.704.
Cosmic neutrinos have not been directly observed, because they are weakly interacting particles. We can compute the relative energy density of neutrinos by relating
the temperature of neutrinos to the temperature of photons in CMB radiation, since
neutrinos were once in equilibrium with the rest of the cosmic plasma. Theory predicts Tν,0 ≈ 0.71 × Tγ,0 = 1.945 K and Ων,0 ≈ 0.68 × Ωγ,0 = 3.40 × 10−5 . WMAP
has found that a cosmic neutrino background is also needed as a part of the standard
model of cosmology.
51
Matter in the universe
Observations have indicated the presence of dark matter in the universe, including
the rotation curves of galaxies, gravitational lensing of background objects by galaxy
clusters, the temperature distribution of hot gas in galaxies and clusters of galaxies,
and the CMB measurement, which can distinguish the dim baryon “dark matter”
from the non-baryonic dark matter.
There are three types of hypothetical dark matter: cold, warm and hot dark matter. Cold dark matter is the dark matter composed of particles with typical speeds
much below the speed of light (generally < 0.1c). Warm dark matter are particles
traveling at relativistic speeds, but less than ultra-relativistic speeds (typically between 0.1c and 0.95c). Hot dark matter are particles that travel at ultra-relativistic
velocities (> 0.95c). Cold dark matter is currently the area of greatest interest for
dark matter research, as hot and warm dark matter do not seem to be viable for
galaxy and galaxy cluster formation.
Most of the matter in the universe is cold dark matter. The measurements of
cosmic abundances of light elements suggest that the baryon density is only a small
fraction of the critical density. From table 3.1, we have Ωb = 0.0456 and Ωc = 0.227.
The cold dark matter constitute about 83% of the matter in the universe. The visible
universe (baryon) only contributes about 17% of the total mass and 4.56% of the
total mass-energy.
Weakly Interacting Massive Particles (WIMPs) are candidates for cold dark matter. These particles interact only through the weak force and gravity. WIMPs do
not interact via electromagnetism, so they cannot be observed directly. They do not
react with atomic nuclei because they do not interact with the strong force either.
There are many experiments currently running (or planned), aiming to search for
WIMPs [116, 117, 118, 119, 120]. WIMPs could also be produced in the laboratory.
Experiments with the Large Hadron Collider (LHC) may be able to detect WIMPs
produced in collisions of the proton beams.
Although WIMPs are a more popular dark matter candidate, there are also experiments searching for other particle candidates. It is also possible that dark matter
52
consists of very heavy hidden sector particles that only interact with ordinary matter
via gravity.
Dark energy in the universe
Dark energy is a hypothetical energy that permeates the entire space and tends
to accelerate the expansion of the universe. Dark energy is the most accepted theory
to explain that the universe is expanding at an accelerating rate [121]. In the ΛCDM
model, dark energy needs to account for 72.8% of the total mass-energy of the universe
(table 3.1) to reconcile the measured flat geometry of space with the total density
equals the critical density. A direct signal of dark energy in a flat universe is from the
late-time Integrated Sachs-Wolfe effect (ISW) [122, 123, 124]. Dark energy is thought
to be homogeneous, and is not known to interact through any of the fundamental
forces other than gravity. With ω < −1/3, dark energy has negative pressure as
gravitational repulsion to accelerate the expension of the universe.
There are two proposed forms for dark energy: the cosmological constant and
scalar fields having a time-dependant energy density. The cosmological constant may
includes the contribution from scalar fields that are constant in time. It may be
difficult to distinguish scalar fields from the cosmological constant because the time
variation of the fields could be extremely small and the value of ω could be very close
to -1.
The simplest explanation for dark energy is the cosmological constant and the
simplest explanation for the cosmological constant is vacuum energy. That is, a
volume of space has some intrinsic, fundamental energy. There are many ways to
predict and estimate this energy, including quantum field theory and string theory.
The cosmological constant remains a subject of theoretical and empirical interest.
The explanation of this small but positive value is still an outstanding challenge.
53
3.4
The Cosmic Microwave Background Radiation
Figure 3.1 shows the timelime of CMB radiation formation. The ΛCDM model
includes the abrupt appearance of expanding space-time containing radiation at temperatures of around 1019 K. The universe was intensely hot, remarkably smooth and
essentially homogeneous. However, small fluctuations in density originating as quantum fluctuations, began to appear and grow. Inflation stretched the curvature of the
universe to be nearly (but not exactly) flat and expanded these quantum fluctuations
in the density of the early universe to the cosmic scale. At redshift (z > 1100), when
the temperature was still above 3000 K, photons were tightly coupled to free electrons
through Thomson scattering. As the universe cooled down to about 3000 K, clumps
of matter (baryons) began to condense and within them protons captured electrons
and became atoms (recombination). Radiation decoupled from matter at 377730+3205
−3200
years (table 3.1) after the Big Bang. The last scattering of the CMB photons was at
redshift of about 1100, at which point the universe was almost exclusively composed
of hydrogen, helium, dark matter, photons and neutrinos. This is the period when the
CMB radiation was last scattered. After that, the CMB photons were free streaming.
The color temperature of the CMB photons has continued to diminish ever since
the Last Scattering Surface (LSS) and now down to about 2.7 K. Their temperature will continue dropping as the universe expands. The radiation from the sky we
measure today comes from the surface of last scattering (figure 3.1). Most of the
radiation energy in the universe is in the CMB radiation, making up a fraction of
roughly 5 × 10−5 (equation 3.30) of the total density of the universe.
Precise measurements of cosmic background radiation are critical to cosmology.
The CMB has a thermal black body spectrum at a temperature of 2.725 K. In the
Planck spectrum, it peaks at the microwave range frequency of about 160.2 GHz,
corresponding to a 1.873 mm wavelength (see appendix B for details).
54
Figure 3.1: Timeline of the universe. The CMB radiation from the last scattering
surface (LSS) when the universe is about 380,000 years old with the temperature of
about 3,000 K [10].
55
Figure 3.2: The internal linear combination map from WMAP [11], showing the all
sky CMB temperature anisotropy.
3.4.1
The CMB Anisotropy
While it is nearly perfectly homogeneous, the CMB radiation does have temperature anisotropy at the level of one part in 105 (figure 3.2). The CMB anisotropy was
firstly measured by COBE (section 3.1.3).
There are two sorts of CMB anisotropy: primary anisotropy, due to effects that
occurred at the last scattering surface and earlier; and secondary anisotropy, due
to effects such as interactions of the CMB radiation with hot gas or gravitational
potentials, which occurred between the last scattering surface and the observer.
To characterize the statistical properties of the CMB temperature T (n̂) on the
celestial sphere, we can expand it in a spherical harmonics basis Ylm as:
T (n̂) =
X
alm Ylm (n̂)
(3.31)
l,m
then the angular power spectrum for our actual sky will be
Clsky =
1 X
|alm |2 .
2l + 1 m
56
(3.32)
The structure of the CMB anisotropy power spectrum is mainly determined by
three effects: initial fluctuations (presumably from inflation), acoustic oscillations and
diffusion damping (collisionless damping).
In the early universe photon-baryon plasma, the pressure of the photons tended
to weaken the anisotropy, while the gravitational attraction from the baryons tended
to strengthen it. These two effects competed to create acoustic oscillations that
generated characteristic peak structures in the CMB power spectrum. The peaks
roughly correspond to the resonances in which the photons decouple when a particular
mode was at its peak amplitude. The WMAP satellite improved the sensitivity and
resolution of the measurements and detected the first three peaks in the angular power
spectrum (figure 3.3). These peaks contain important physical signatures about the
universe: The angular scale of the first peak determines the curvature of the universe.
The amplitude ratio of the first and second peak determines the baryon density. The
amplitude of all three peaks is related to the dark matter density. The locations of
the peaks also give important information about the nature of the geometry. More
power spectrum peaks at higher multipole moment have been measured by ACBAR
[125], ACT [126, 127] and SPT [128].
Collisionless damping was caused by two effects: the increasing mean free path of
the photons as the primordial plasma rarefied when the universe expanded and the
finite depth of the LSS, which caused the mean free path to increase rapidly during
decoupling, while some Thomson scattering was still occurring.
3.4.2
The CMB Polarization
CMB polarization arose from the Thomson scattering of the CMB photons at
the LSS. As shown in figure 3.4, when an electromagnetic wave is incident on a free
electron (from x or y direction), the scattered wave is polarized perpendicular to the
incidence direction (z direction). If the incident radiation is isotropic or has only a
dipole variation, the scattered radiation would have no net polarization (xp1 = yp1).
However, if the incident radiation from perpendicular directions (x and y) have different intensities, a net linear polarization would result (xp1 6= yp1). Such anisotropy
57
Figure 3.3: The angular power spectrum from WMAP [12], showing the detection of
the first three peaks. The first peak is at ℓ ≈ 220, corresponding to an angular scale
of about 1◦ .
have a quadrupole pattern. At the LSS, there was temperature inhomogeneity. So
the scattered radiation is polarized.
There were three different perturbations in the early universe plasma: scalar,
vector and tensor perturbation. The scalar perturbation was the energy density fluctuations in the plasma that caused velocity distributions. The fluid velocity from hot
to colder regions caused blueshift of the photons, resulting in quadrupole anisotropy.
The vector perturbation was the vorticity in the plasma that caused Doppler shifts.
However, vorticity would be damped by inflation and is expected to be negligible. The
tensor perturbation is from the inflationary gravitational waves that stretched and
squeezed space in orthogonal directions (+, ×), which also stretches the wavelength
of radiation.
The above perturbations result in two types of polarization in the CMB radiation,
called E-modes and B-modes (in analogy to electromagnetism) [129]. The E-modes,
curl-free components with no handedness, are due to both the scalar and tensor
perturbations. The B-modes, curl components, are due to only tensor perturbations
58
(hot radiaon)
X
E>0
E<0
xp1
xp2
yp2
eY
yp1
(cold radiaon)
xp1
B>0
yp1
B<0
Z
(polarizaon)
Figure 3.4: Left: Quadrupole polarization from Thomson scattering of the CMB
photons with free electrons. Right: The E and B mode patterns. The E-modes are
curl-free components with no handedness. The B-modes are curl components with
handedness.
because of their handedness (figure 3.4). The amplitudes of tensor and scalar ratio is
parametrized by the tensor-to-scalar ratio (r), which is related to the energy scale of
inflation.
Similar to the temperature anisotropy, the CMB polarization at each point on the
sky can be characterized by combining its Q and U Stokes parameters (section 1.2)
in terms of spin-2 spherical harmonics:
Q(n̂) ± iU(n̂) =
X
lm
a∓2,lm
∓2 Ylm (n̂)
(3.33)
then we decompose them into E- and B-like components:
a±2,lm = Elm ± iBlm .
(3.34)
These Elm and Blm parameters can be estimated from polarization maps as for
the temperature anisotropy spectrum. Additionally, the cross-correlation between the
temperature and the polarization can be taken. Figure 3.5 shows the TE, EE, and
BB power spectra measured by WMAP [13].
59
Figure 3.5: Plots of signal for TT (black), TE (red ), and EE ( green). The notyet-detected BB (blue dots) signal is from a model with r = 0.3. The BB lensing
signal is shown as a blue dashed line. The foreground model for synchrotron plus
dust emission is shown as straight dashed lines [13].
60
The E-modes polarization had been measured over a range of angular scales [130,
131]. The B-modes, which have not been detected, are expected to be extraordinarily
faint. To set meaningful limits on inflationary models, any experiment designed to
detect the inflationary B-mode signal should have a polarization sensitivity near 30
nK. That is 10−8 of the CMB blackbody temperature and 10−3 of the primordial
CMB temperature anisotropy. The B-mode observation provides the only known way
to measure the energy scale of inflation since inflation produced these gravitational
waves whose amplitude depends only on the energy scale at which inflation occurred.
Detection of B-modes would also be the first ever direct detection of gravitational
waves.
61
Chapter 4
The Cosmology Large Angular
Scale Surveyor (CLASS)
In chapter 3, we discussed the origin and evolution of the universe. A fundamental
question is, “Did inflation really happen?” Inflation posits that the universe grew from
quantum fluctuations of the vacuum driven by negative pressure energy to expand
exponentially to astronomical scales. The simplest (and therefore most compelling)
versions of inflation produce a stochastic background of gravitational waves whose
amplitude depends only on the energy scale at which inflation occurred. The gravitational waves imprint a polarization pattern on the CMB (B-mode polarization), that
then provides a direct way to measure the energy scale of inflation (section 3.4.2).
Measurements to date of the E-mode signal are consistent with the predictions
of anisotropic Thompson scattering [130, 131], while the B-mode signal has yet to
be detected. The B-mode power spectrum amplitude can be parameterized by the
relative amplitude of the tensor to scalar modes (the tensor-to-scalar ratio), given by
r≡
∆2h (k0 )
,
∆2ℜ (k0 )
(4.1)
where, ∆2ℜ (k) and ∆2h (k) denote the dimensionless scalar and tensor power spectra, ℜ
denotes the intrinsic curvature perturbation, h denotes the amplitude of gravitational
waves, and k0 is some pivot wavenumber [132, 133].
62
Figure 4.1: Two-dimensional joint marginalized constraint (68% and 95% CL) on
scalar spectral index (ns ) and tensor to scalar ratio (r), derived from the data combination of WMAP + BAO + H0 [14]. Three linear fits are from different simple
inflation models.
If inflation produced the structure we see today, and it is associated with the
energy scale (∼ 1016 GeV) of grand unified theories (GUTs) [134], then r ≥ 0.01 (for
the simplest models). The current upper limit, inferred from WMAP + BAO + H0 is
r < 0.24 (Table 3.1). The WMAP + BAO + H0 data also show 3σ deviation from a
scale-invariant (scalar spectra index, ns = 1.0) scalar perturbation spectrum, with ns
= 0.963 ± 0.012 [14]. For the simplest inflation models (see figure 4.1), this expected
deviation from scale invariance is coupled to gravitational waves with r ≈ 0.10. These
considerations establish a strong motivation to search for this remnant from when the
universe was about 10−32 seconds old.
The Cosmology Large Angular Scale Surveyor (CLASS) is an experiment with an
unprecedented ability to detect the B-mode polarization to the level of r ≤ 0.01. It
consists of 4 ground-based wide-field polarimeters, operating at 40, 90 and 150 GHz.
CLASS will measure the large angular scale CMB polarization signature by observing
∼ 65% of the sky above 45◦ elevation from the Atacama Desert, 5180 meters above
sea level (figure 4.2).
63
Figure 4.2: The background is the WMAP 7 year all sky Q band polarization map in
Galactic coordinates showing the sky coverage of CLASS experiment. Observing from
the Atacama Desert in Chile, CLASS covers ∼ 65.1% of the sky above 45◦ elevation.
Excluding the Galactic mask area, the visible sky left is ∼ 46.8% (bright region). The
dark circle at the south pole is about 22◦ in radius. Figure courtesy of David Larson.
As shown in figure 4.3, each CLASS telescope has a large front-end polarization
modulator, called Variable-delay Polarization Modulator (VPM) (section 4.3), that
rapidly modulates the polarization sensitivity for each observed sky pixel with no
reliance on spatial scanning. Each of CLASS’s telescopes is a diffraction limited
catadioptric system (section 4.4). The optics are fast (f/2.0) and have a large field of
view (FOV), low cross-polarization and high Strehl ratio across the FOV. On the focal
planes (section 4.5), the smooth-walled feedhorn arrays couple the radiation from the
optics to transition edge sensor (TES) bolometer detectors. The focal planes and
detectors are cooled to about 100 mK.
4.1
Scientific Overview
Table 4.1 shows the CLASS scientific overview. It lists the main challenges of Bmode detection and the solutions to them that CLASS provides. The B-mode signal
64
Figure 4.3: CLASS instrument overview for the 40 GHz band. The instrument consists a front-end variable-delay polarization modulator, catadioptric optic system and
a field cryostat. The lenses are cooled to about 4 K and the smooth-walled feedhorncoupled TES bolometer array operates at 100 mK. Figure courtesy of Joseph Eimer.
65
Table 4.1: CLASS Scientific Overview
B mode challenge
Requirement
CLASS solution
B-mode signal
Systematic control
Polarization modulator
is small
is essential
at front of optics
Noise is
Large number
4 telescopes
dominated
of detectors
4 focal planes
by
with
396 pixels
atmosphere
low noise
792 TESs
Foregrounds are
Polarization must
40 GHz: 36 detector pairs
polarized: Synchrotron,
be measured at
90 GHz: 300 detector pairs
polarized dust emission multiple frequencies 150 GHz: 60 detector pairs
At small angular
Separate lensing
Focus on large
scales, gravitational
B-modes from
angular scales
lensing converts E → B inflationary B-modes
(∼ 65% sky coverage)
is predicted to be extremely weak (∼ 30 nK) and hides behind the 2.725 K CMB
monopole signal, which requires the experiment to be designed to minimize systematic measurement errors. The critical front-end VPM can minimize the systematic
error by separating the instrumental effects from sky signals. It modulates the very
large angular scale polarization rapidly (> 3 Hz) to remove 1/f noise. Because the
polarization signal is spatially correlated, relying on the usual approach (scanning
to remove 1/f noise) will convert unpolarized structure into false polarization signals. The CLASS objective is to avoid spatial scanning to remove 1/f noise. This
instrument modulates polarization at the front-end with a small motion over a large
aperture. It combines an unprecedented sensitivity to the inflationary B-mode signal
with powerful systematic error suppression.
Since CLASS is a ground-based experiment, the signal is dominated by photon
noise from the atmosphere and the instrument (see section 4.2.2 for details). Sensitivity requirements demand a combination of substantial observing time with a large
numbers of detectors, each operating well below the background limit. CLASS has
792 TES bolometers operating at 100 mK in 4 different focal planes. These are novel
integrated focal planes that combine the clean beam properties of smooth-walled feedhorns with planar microwave filters and sensitive TES bolometers, which have been
66
demonstrated in astronomical instruments [135].
To characterize the Galactic foreground contamination from synchrotron and polarized dust emission (section 1.4), CLASS observes in three frequency bands (40,
90 and 150 GHz), accessible from the ground, as seen in figure 4.4. The data from
these bands will be used to characterize the foreground signals for subsequent removal. Free-free emission is unpolarized so it does not affect the CMB polarization
measurement.
Gravitational lensing can convert E-mode polarization to B-mode polarization in
small angular scales, but on large angular scales inflation is the only known extragalactic source of B-mode polarization. Thus, observations of the large angular scale
CMB polarization signals provide a clean way to directly verify inflation and measure
the energy scale of inflation [136]. By targeting the large scale “reionization bump” of
the B-mode signal at l ≤ 10, where the B-mode signal emerges most clearly from the
gravitational lensing foreground, CLASS avoids gravitational lensing contamination
(see section 4.2).
In summary, the CLASS experiment has the following design criteria for B-mode
searching: (1) Improves instrument sensitivity by using a larger number of background limited detectors; (2) Achieves excellent systematic control by placing the
polarization modulator at front of the optics; (3) Observes in multi-waveband for
foreground removal. (4) Focuses on large angular scale to avoid gravitational lensing
contamination.
4.2
Sensitivity Calculation and Bandpass Optimization
Figure 4.4 shows the results of CLASS waveband optimization and sensitivity
calculation. CLASS observing near the frequency of minimum Galactic foregrounds,
achieves maximum sensitivity to the level of r ∼ 0.01 at the “reionization bump”
and avoids the lensing contamination that dominates at small scales. Additional
experiments, such as PIPER [137], SPIDER [138], and EBEX [139] will take various
67
PIPER Bands
OO)& O%%π[µK2]
90 GHz Band
$QWHQQD
7HPSHUDWXUHµ.
V\QFK
(PRGHV
GXVW
Reionization
Bump
DASI
QUaD
WMAP
BICEP
U U CBI
BOOMERanG
%PRGHV
ing
Lens
Grav.
U CAPMAP
150 GHz Band
40 GHz Band
$WPRVSKHULF
7UDQVPLVVLRQ
)UHTXHQF\*+]
Multipole Moment O
Figure 4.4: CLASS wavebands and sensitivity curve from [15]. Left: The frequency
bands of CLASS are chosen to straddle the Galactic foreground spectral minimum
and to minimize atmospheric effects (see section 4.2.2). Right: The CLASS sensitivity
curve, shown by the dashed curve along the shaded boundary, is the 1σ limit for each
l and assumes 3 years of observing with a conservative 50% efficiency for down-time
(see section 4.2.1). CLASS has the sensitivity to definitively detect B-modes at the
cosmologically interesting limit of r ∼ 0.01.
approaches that are complementary to CLASS.
4.2.1
Sensitivity Calculation
The sensitivity calculation is based on the sky coverage, instrument beam size,
efficiency, number and sensitivity of the detectors and total integration time. In
far-IR to millimeter waveband, detector sensitivity is normally quoted as NEP, that
can also be converted to other instrument-specific parameters, such as NEFD (see
section 2.2), NET or NEQ:
Definition of NEP, NET and NEQ
Noise Equivalent Power (NEP) is a measure of the sensitivity of a detector normally used in astronomy. It is defined as the signal power that gives a unity signalto-noise ratio in a 1 Hertz output bandwidth [140]. Base on the Nyquist-Shannon
sampling theorem, an output bandwidth of 1 Hertz is equivalent to half a second of
68
integration time. NEP is a detector-specific parameter. It has the unit of WHz−1/2 .
NET is Noise Equivalent Temperature. It is defined as the signal (in temperature
units) from a source needed to produce a signal-to-noise ratio value of unity in a 1.0
second integration [141]. It is an instrument-specific parameter and quoted in units
of µKs1/2 .
To measure polarization signal, we have an equivalent definition to the NET, that
is Noise Equivalent Q Stokes parameter (NEQ). It is defined as the polarized signal
from a linearly polarized source aligned with the detector orientation that is required
to produce a signal-to-noise ratio value of unity in a 1.0 second integration. It is also
quoted in units of µKs1/2 .
The above definitions can be quoted for a single detector or a pair of detectors
following the relations:
NEPs =
NETs =
NEQs =
√
√
√
2NEPp
2NETp
2NEQp
(4.2)
where the indices “s” means a single detector and “p” means a detector pair.
The conversion between NET and NEP is [142]:
NET = √
NEP
2ηd ηt AΩ∆ν∂Bν /∂T
(4.3)
where, ηd and ηt are the detector and instrument efficiencies, AΩ describes the optics,
∆ν is the bandwidth and ∂Bν /∂T is the derivative of the source emission (the CMB)
√
with respect to temperature (Tcmb ). The factor of 2 is from the conversion between
Hz and second. We also have [141]:
NEQs =
√
√
2NEQp = 2NETs = 2 2NETp
Table 4.2 shows CLASS detector sensitivities in NEQp .
69
(4.4)
Table 4.2: CLASS Detector Parameters
Channel
40 GHz 90 GHz
Number of pixels (detector pair) (Np )
36
300
Number of detectors (Ns )
72
600
Beamsize (◦ )
1.50
0.67
NETp of detector (µKs1/2 )
68
60
1/2
NEQp of detector (µKs )
135
120
150 GHz
60
120
0.40
93
186
Beamsize and Window Function
1
For a Gaussian beam, the beamsize is normally defined as the full width at half
maximum (FWHM). Then, the standard deviation of the beamsize can be written as:
FWHM
σbeam = √
.
8ln2
(4.5)
Under the flat-sky approximation, the solid angle of the beam will be:
2
Ωbeam = 2πσbeam
because the integral over a Gaussian plane with unit height gives:
2
Z Z
x + y2
exp −
dxdy = 2πσ 2 .
2σ 2
(4.6)
(4.7)
The window function is a function that contains information about the beamsize
and chopping angle of the experiment [143]. For a Gaussian beam, in multipole-space
it can be written as:
2
ωℓ = exp[−ℓ(ℓ + 1)σbeam
].
(4.8)
Noise Power Spectra
2
The noise of the Q or U measurement is given by:
2
σQ
NEQ2p
NEQ2s
=
=
(ηd ηt )2 Np tpix
(ηd ηt )2 Ns tpix
where tpix is the integration time for each pixel (beam).
1
2
This section is mostly from [142]
This section is mostly from [142]
70
(4.9)
For an experiment with fsky coverage, Ωbeam beam solid angle, tobs total observation time and ηobs observation efficiency (e.g., including precipitable water effects),
assuming the experiment scans uniformly across the sky, then
ηobs tobs Ωbeam
4πfsky
=
.
tpix = ηobs tobs /
Ωbeam
4πfsky
(4.10)
For Gaussian white noise on the sky, where the Q and U measurements in each
beam-sized pixel are uncorrelated with each other and with the Q and U values in
every other pixel, the noise power in E and B modes is:
2
NℓBB = NℓEE = Ωbeam σQ
.
Then the expected error in the CℓBB measurement is:
s
2
NℓBB
BB
BB
∆Cℓ =
Cℓ +
(2ℓ + 1)fsky
ωℓ
(4.11)
(4.12)
By substituting equation 4.5 - equation 4.11 in to equation 4.12, we have:
s
4πfsky NEQ2p
2
2
∆CℓBB =
{CℓBB +
exp[ℓ(ℓ + 1)σbeam
]}
(4.13)
(2ℓ + 1)fsky
ηobs (ηd ηt )2 tobs Np
To calculate the CLASS sensitivity (see figure 4.4), we used the NEQ2p , Np and
σbeam values listed in table 4.2 and assumed tobs = 3 years, ηobs = 50%, ηd ηt = 0.80,
fsky = 65% and CℓBB is from the current upper limit of r ≈ 0.2.
4.2.2
Bandpass Optimization
The scientific goal of the CLASS project is to detect the B-mode polarization of
the CMB. To calculate the instrument signal-to-noise ratio, we should use the Bmode polarization as our signal. However, the B-mode has not yet been detected. By
assuming the B-mode signal is a tiny fraction of (and is proportional to) the CMB
monopole (black body radiation with T = 2.725 K), in a given bandwidth, we can
calculate the relative signal-to-noise ratio by using the CMB monopole spectrum as
our signal. Observing from the ground, the dominant noise of CLASS is from atmospheric emission. In the signal-to-noise ratio calculation, we should also take the
71
efficiency of the VPM into account, since it depends on the bandwidth. The bandwidth optimization is based on maximizing the total signal-to-noise ratio integrated
over each of these bandwidths.
Atmosphere Model
The Atmospheric Transmission at Microwaves (ATM) model [144] was used to
calculate the transmission of the atmosphere at the CLASS site - Chajnantor Plateau,
Chile. The ATM model was improved from many widely used older models such as
the Microwave Propagation Model (MPM) [145]. It has been developed to perform
radiative transfer calculations trough the terrestrial atmosphere. ATM treats the
clear sky case to evaluate absorption/emissivity, but also polarization and scattering
effects. It is currently used by several millimeter/subllimeter wave telescopes such as
the Atacama Large Millimeter Array (ALMA) to evaluate atmospheric transmission
and phase dispersion. Validation of this model has been undertaken with a series of
observational experiments using a Fourier Transform Spectrometer (FTS) installed
at the Caltech Submillimeter Observatory (CSO) [146].
CLASS will be deployed at Chajnantor Plateau, close to the Atacama Pathfinder
Experiment (APEX) telescope. According to the site testing result from the APEX
(figure 4.5), it is reasonable to have the annual Precipitable Water Vapor (PWV)
as 1.0 mm. Figure 4.6 shows the ATM model of the atmosperic transmission and
brightness temperature from 5 to 1000 GHz at 45◦ elevation with PWV = 1.0 mm.
There are 3 main atmosphere windows below 200 GHz, centered at about 40, 90
and 150 GHz. As shown in figure 1.4, the 40 GHz band can be used to characterize
the synchrotron foreground radiation and the 150 GHz band data can be used to do
polarized dust foreground removal. CLASS has two polarimeters operating at 90 GHz
band, near the minimum of the foreground contamination.
Signal to Noise Ratio
The NEP of a bolometer can be described by [147]:
72
Figure 4.5: Annual variation of the Precipitable Water Vapor (PWV) content at
Chajnantor, based on 10 years of site testing. Conditions are worse during the winter
from the end of December to early April. The expected median PWV for the rest of
the year is around 1 mm, while conditions of PWV < 0.5 mm can be expected up to
25% of the time [16].
73
Atmospheric Transmission
1
Atmospheric Brightness Temperature
300
0.9
250
Brightness Temperature (K)
0.8
Transmission
0.7
0.6
0.5
0.4
0.3
0.2
200
150
100
50
0.1
0
0
100
200
300
400 500 600
Frequency (GHz)
700
800
0
0
900 1000
100
200
300
400 500 600
Frequency (GHz)
700
800
900 1000
Figure 4.6: Atmospheric transmission and brightness temperature at CLASS site from
5 to 1000 GHz. ATM parameters: ground temperature = 275 K, ground pressure
= 558 mb, PWV = 1.0 mm, elevation = 45◦ , altidude = 5180 m. ATM version:
atm2011 03 15.exe.
NEP2 = NEP2Johnson + NEP2thermal + NEP2photon
+ NEP2load + NEP2amplifier + NEP2excess . (4.14)
Since detectors for the CLASS experiment are background limited, NEP2photon from
atmosphere and instrument dominates over other sources of noise. In a black-body
radiation field, NEP2photon can be written as [147] (see appendix C for details):
NEP2photon
AΩ (kB Ts )5
=4 2
c
h3
Z
x4
αǫf
1+ x
(αǫf )dx
ex − 1
e −1
(4.15)
Where AΩ describes the optics, f is the transmissivity of the optics, Ts is the temperature of the source, ǫ is the emissivity of the source, α is the detector absorptivity,
α, ǫ, and f are evaluated at ν, and x = hν/(kB Ts ).
The atmosphere is treated as a blackbody source with varying emissivity:
2hν 3 /c2
Iν =
ǫ
(4.16)
ehν/(kB Ts ) − 1
where Iν is the intensity of the atmosphere emission.
74
The number of photons in a given state x is:
n(ν) = n(x) =
αǫf
.
−1
ex
From equation 4.16 and equation 4.17 , we have:
αf c2
2hν 3 /c2
x
=
n = αf Iν /(e − 1)/ hν/(k Ts )
Iν .
B
e
−1
2hν 3
(4.17)
(4.18)
Equation 4.15 can be written in n as:
NEP2photon
Z
AΩh2 (kB Ts )5
=4 2
n(1 + n)ν 4 dν
c
h3
Z
Z
h2
2
4
=4 2
AΩn(1 + n)ν dν = 4h
n(1 + n)ν 2 dν
c
(4.19)
where AΩ = c2 /ν 2 for diffraction-limited optics.
The CMB signal has a blackbody spectrum. Since NEP is the standard deviation
in power from a 0.5 second integration, our signal is
Z
Z
hν
2hν 3 /c2
dν = αf ξ hν/(k T )
dν
S = (0.5 s) AΩαf ξ hν/(k T )
B
B
cmb
cmb − 1
e
−1
e
(4.20)
where ξ is the transmission of the atmosphere.
From equation 4.19 and equation 4.20, we have:
R ν2
αf ξhν/(ehν/(kB Tcmb ) − 1)dν
S
S
ν1
Rν
=
=
N
NEP
(4h2 ν12 n(1 + n)ν 2 dν)1/2
(4.21)
for the waveband between ν1 and ν2 . This equation teats the atmosphere with a
single temperature model and does not include the loading from the instrument.
Optimization Results
The VPM efficiency is strongly depend on its operational bandwidth (see section 4.3.4 for details). Theoretically, we should absorb the VPM efficiency into the
coefficient f in equation 4.21 to calculate the total signal-to-noise ratio, but this would
result in complicated calculations. As an approximation, we multiply equation 4.21
by equation 4.55 to get the total relative signal-to-noise ratio:
R ν2
αf ξhν/(ehν/(kB Tcmb ) − 1)dν
ν1
Rν
SNR ∝ η(ν2 /ν1 )
(4h2 ν12 n(1 + n)ν 2 dν)1/2
75
(4.22)
The ATM model provides the transmission (ξν ) and brightness temperature (Tν )
of the atmosphere (figure 4.6). One can calculate the emission intensity Iν from Tν
using the Planck function:
1
2hν 3
2
hν/(k
Tν ) − 1
B
c e
(4.23)
αf c2
αf
Iν = hν/(k Tν )
.
3
B
2hν
e
−1
(4.24)
Iν =
then, from equation 4.18, we have:
n=
We can calculate the relative signal-to-noise ratio numerically by substituting
equation 4.55 and equation 4.24 into equation 4.22. The bandwidths were optimized
by maximizing the signal-to-noise ratio value.
Figure 4.7 shows the CMB signal transmitted through the atmosphere (equation 4.20) and atmosphere emission intensity (equation 4.16) for the relative signalto-noise ratio calculation (equation 4.21). Figure 4.8 shows the result of the optimization. The 2-D plot of relative signal-to-noise ratio over 0 to 200 GHz shows 3 local
maxima in the bandwidth from 0 to 200 GHz. They are located at (30.3 GHz, 40.3
GHz), (77.3 GHz, 108.3 GHz) and (126.8 GHz, 164.3 GHz). For the 40 GHz band,
we search for the maximum in the range of ν > 30 GHz.
In this model, we assumed αf = constant across the bandwidths, and found that
within the tolerance of the optimization (0.02 GHz), in the range of 0.5 ≤ αf ≤ 1.0,
the optimization result does not depend on the αf value. We also found that the
optimization of equation 4.21 and equation 4.22 gave the same result. The VPM
efficiency does not affect the optimization.
The above are the results from relative signal-to-noise ratio optimization only. As
we can see in figure 4.8, the plot does not show strong gradients around the peaks.
The nearby points can also provide a similar signal-to-noise ratio level. We should
take into account other instrument effects, such as the bandwidth limit of a feedhorn.
The 40 GHz bandwidth is set to be 33.0 GHz to 43.0 GHz. The 90 and 150 GHz
bands have not been fixed yet.
76
−18
4
x 10
CMB x Atmosphere Transmission
Intensity [W Hz−1 m−2 sr−2]
3.5
3
2.5
2
1.5
1
0.5
0
0
20
−15
x 10
40
60
80 100 120 140
Frequency [GHz]
160
180
200
180
200
Atmosphere Emission Intensity
Intensity [W Hz−1 m−2 sr−2]
2.5
2
1.5
1
0.5
0
0
20
40
60
80 100 120 140
Frequency [GHz]
160
Figure 4.7: Top: the CMB signal (equation 4.20) and Bottom: atmospheric noise
source (equation 4.16) for the relative signal-to-noise ratio calculation (equation 4.21).
The red, green and blue lines shows our optimized bandwidth for 40, 90 and 150 GHz
band: (30.3 GHz - 40.3 GHz), (77.3 GHz - 108.3 GHz) and (126.8 GHz - 164.3 GHz).
77
Relative Signal to Noise Ratio
3
20
40
2.5
Frequency [GHz]
60
2
80
100
1.5
120
1
140
160
0.5
180
200
20
40
60
80 100 120 140 160 180 200
Frequency [GHz]
0
Figure 4.8: The 2-D plot of relative signal-to-noise ratio (equation 4.22) from 0 to
200 GHz showing our optimization results. The cross points of red, green and white
lines are the locations of the local maxima. For the 40 GHz band, we only search for
the maximum in the range of ν > 30 GHz. The coordinates are (30.3, 40.3), (77.3,
108.3) and (126.8, 164.3).
78
V (circular)
V (circular)
U
U
Q
Q
VPM
HWP
Figure 4.9: As shown in Poincaré sphere, VPM modulates between Q and V , while
the HWP mix Q and U. In the case of VPM, the residuals due to the spectral effects
(shown in blue) are a function of measurable modulation parameters. Figure courtesy
of David Chuss.
4.3
The Variable-delay Polarization Modulator
VPM is the the first element of CLASS instrument. It modulates the sky polarization signal by introducing a controlled variable path difference between two orthogonal linear polarizations of the incident radiation. Compared to the conventional
spinning Half Wave Plate (HWP), the advantages of the VPM can be summarized
as follows: [148] (1) The VPM is used in reflection, eliminating the effects from the
dielectrics (e.g., nonuniformity, birefringence, ...); (2) The VPM modulation employs
small motions, making it easier to achieve rapid modulation; (3) The VPM has more
flexibility in size than the HWP. This allows larger apertures that enable front-end
modulators for low frequency systems; (4) The modulation symmetry of the VPM
allows spectro-polarimetry; (5) The VPM does not convert between Stokes Q and U,
as opposed to the HWP (figure 4.9).
79
Grid
d
Mirror
Figure 4.10: VPM modulates polarization by introducing a controlled variable path
difference between two orthogonal linear polarizations. Dots show the component
with polarization angle parallel to the grid; Double arrow show that with angle perpendicular to the grid. By moving the mirror up and down, VPM introduces a path
difference x(t) = 2d(t)cosθ between these two orthogonal polarization components.
4.3.1
Polarization Transfer Function
As shown in figure 4.10, the VPM is made of a polarizing wire grid (the wires
only run one direction in this grid) and a movable parallel mirror behind it. The
polarized radiation from sky can be decomposed into two orthogonal components:
The component with polarization angle parallel to the grid will be reflected by the
wire grid, the component with angle perpendicular to the grid will pass through the
grid and get reflected by the mirror. For an ideal VPM, the optical path difference
between these two components is [149]:
x = 2dcosθ,
(4.25)
where d is the grid-mirror separation, θ is the incident angle.
An ideal VPM is equivalent to a birefringent plate with its birefringent axis oriented at an angle α with a delay φ followed by a reflection. The Mueller matrix for
a VPM system can be written as [150]:
80


1
0
0
0


0 cos2 2α + cosφsin2 2α −sin2αcos2α(1 − cosφ) sin2αsinφ 


Mvpm (α, φ) = 

2
2
0 sin2αcos2α(1 − cosφ) −sin 2α − cosφcos 2α −cos2αsinφ


0
sin2αsinφ
cos2αsinφ
−cosφ
(4.26)
where, in the long wavelength limit,
φ = kx = 2kdcosθ
(4.27)
is the phase delay, k is wave number, α is the angle of the grid with respect to the
orientation of detectors.
By setting α = 45◦ , we have:
 
I
 
Q
 
 
U 
 
V
det
 
I
 
Q
 
= Mvpm  
U 
 
V
sky
 

I
1
0
0
0
 


0 cosφ 0

sinφ  Q


=
 
 
0
0
−1
0 

 U 
V
0 sinφ 0 −cosφ
.
(4.28)
sky
Then, for a detector sensitive to Stokes Q, the signal at the detector will be:
Qdet = Qsky cosφ + Vsky sinφ
(4.29)
Equation 4.29 is the polarization transfer function describing the way that a VPM
modulates the incident polarized signal. The key to understanding this polarization
transfer function is to determine how the phase delay, φ, is related to the grid-mirror
separation, d, since the latter is the quantity that can be directly measured in an
instrumental setup.
4.3.2
VPM Grid Optimization
To optimize the performance of a wire grid, analytical approximations suggest
a desire to achieve λ ≫ a and 2a/g ≈ 1/π, where λ is the wavelength, a is the
81
7
Figure 4.11: The wire grid performances for two different wavelengths from a simulation [17]. In the limit of g/λ ≪ 1, a sinusoidal form for Stokes Q is in good agreement
with an ideal grid (equation 4.29). The VPM reflection phase delay differs from the
free-space grid-mirror delay if the conditions are changed.
radius of the wire, g is the center-to-center wire pitch. Larger 2a/g leads to higher
reflection for both parallel and perpendicular polarization components. Grids with
2a/g ≈ 1/π allow high enough reflective for the parallel component and at the mean
time enable high transmissive for the perpendicular component. A transmission line
model has been developed to simulate to performance of a VPM grid in a range of
0.02 < 2a/g < 1.00 [17].
Figure 4.11 shows the polarization transfer function for a single frequency of two
models with different geometric limit. For plane wave illumination with λ ≫ a, equation 4.27 is a good approximation for the VPM phase delay. As the wire diameter
becomes a finite fraction of a wavelength, the polarization response remains a sinusoidal function of the phase delay; however, the VPM reflection phase is dependent
upon the details of the grid geometry.
82
4.3.3
VPM Mirror Throw Optimization
In the above discussion, a VPM grid with λ ≫ a and 2a/g ≈ 1/π is a reasonable
approximation to an ideal VPM. This section will focus on the optimization of the
mirror throw for an ideal VPM base on maximizing the signal-to-noise ratio of its
output.
From equation 4.29, for a given bandpass kl to kh , the average output signal of an
ideal VPM as a function of x is:
Z kh
1
S(x) =
[I(k) + Q(k)cos(kx) + V (k)sin(kx)]dk
2(kh − kl ) kl
(4.30)
where, I(k), Q(k), V (k) are the stokes parameters of the incident signal from the sky,
kl and kh are the wave numbers of the lower and higher limit of the waveband.
In CLASS wavebands, the atmospheric transmission is high and roughly constant
(figure 4.6), thus I(k), Q(k) and V (k) can be fit by a black body spectrum (∝
AΩBν (T )):
k
I0 k
ehν/(kB Tcmb ) − 1
eAk − 1
Q0 k
k
= Ak
Q(k) = Q0 hν/(k T )
B
cmb
e
−1
e −1
V0 k
k
= Ak
V (k) = V0 hν/(k T )
B cmb − 1
e
e −1
I(k) = I0
=
(4.31)
where, I0 , Q0 , V0 are constants and A = hc/(2πkB Tcmb ).
Then, equation 4.30 can be written as:
1
S(x) =
2(kh − kl )
Z
kh
kl
I0 k
Q0 k
V0 k
+
cos(kx) + Ak
sin(kx) dk
eAk − 1 eAk − 1
e −1
= SI × I0 + SQ (x) × Q0 + SV (x) × V0
83
(4.32)
where,
1
SI =
2(kh − kl )
SQ =
SV =
1
2(kh − kl )
1
2(kh − kl )
Z
kh
kl
kh
Z
kl
kh
Z
kl
k
dk = constant
−1
eAk
kcos(kx)
dk
eAk − 1
ksin(kx)
dk.
eAk − 1
(4.33)
“Cosine” and “Linear” are two candidate VPM mirror chopping modes. The
chopping can be approximated by N discrete steps as:
d(i) =
(
p0 + ∆p × (cos(i/(N − 1) ∗ π) + 1)/2
p0 + ∆p × (i/(N − 1))
Cosine mode
Linear mode
(4.34)
where p0 is the starting position of the mirror, ∆p is the peak-to-peak mirror throw
and i is an integer in the range of (0, 1, ..., N − 1) and the optical path difference is:
x(i) = 2d(i)cosθ
(4.35)
Then, equation 4.32 can be written in matrix format:
AX = s
where

(4.36)

SI (0)
SQ (0)
SV (0)


 S (1)
SQ (1)
SV (1) 


I


,
A=
...
...
...




SI (N − 2) SQ (N − 2) SV (N − 2)


SI (N − 1) SQ (N − 1) SV (N − 1)
 
I0
 

X=
Q0 
V0
84
(4.37)
(4.38)
and


S(0)


 S(1) 




.
s=
...




S(N − 2)


S(N − 1)
(4.39)
All elements in A can be calculated by substituting equation 4.35 and equation 4.34 into equation 4.33. For a given signal matrix s, We can solve equation 4.36
for X and its covariance matrix CovX:
X = (AT A)−1 AT s
(4.40)
CovX = (AT A)−1
(4.41)
Theoretically, both X and CovX should be diagonal matrices, since Q and V noise
are uncorrelated. Then, the relative signal-to-noise ratio will be:
P
Q
|SQ (i)|
(4.42)
SNQ =
∝ √
σQ
CovX22
P
V
|SV (i)|
SNV =
(4.43)
∝ √
σV
CovX33
The CLASS VPM mirror throw is optimized by maximizing the relative signal-tonoise ratio for Stokes Q. The parameters in our calculation are as following: p0 and
∆p are in the range of 0.01 λ0 to 1.00 λ0 , with the step size of 0.01 λ0 and N = 100.
Based on these setting, the resolution is 79 µm for the 40 GHz band, 32 µm for 90
GHz and 21 µm for the 150 GHz band.
Figure 4.12 and figure 4.13 show the optimization plots of “cosine” and “linear”
chopping modes for the 40 GHz band. In the plots, the relative signal-to-noise ratios
are normalized to the peak values. The details are listed in table 4.3. For the “cosine”
mode, (0.19 λ0 , 0.39 λ0 ) is preferred, while the “linear” mode prefers (0.46 λ0 , 0.16 λ0 ).
The peak relative signal-to-noise ratio of the “cosine” mode is 6.4 × 105 and 5.4 × 105
for the “linear” mode. The “cosine” chopping mode offers a higher signal-to-noise
ratio than that from the “linear” mode.
85
1
0.9
0.9
0.8
0.7
0.7
0
Mirror Start Position (λ )
0.8
0.6
0.6
0.5
0.5
0.4
0.4
0.3
0.3
0.2
0.2
0.1
0.1
0.1
0.2
0.3
0.4
0.5
0.6
0.7
Peak to Peak Throw (λ )
0.8
0.9
1
0
Figure 4.12: The contour plot of relative signal-to-noise ratio for Stokes Q, calculated
from equation 4.42 with cosine chopping mode. This plot is for the 40 GHz band (33
GHz to 43 GHz, λ0 = 7.89 mm). The maximum is at (0.19 λ0 , 0.13 λ0 ) with the peak
signal-to-noise ratio scaled to be 1.00. There are 4 other local maxima nearby: (0.19
λ0 , 0.39 λ0 ), (0.44 λ0 , 0.13 λ0 ), (0.44 λ0 , 0.39 λ0 ) and (0.27 λ0 , 0.26 λ0 ). Details are
listed in table 4.3.
86
1
0.9
0.9
0.8
0.7
0.7
0
Mirror Start Position (λ )
0.8
0.6
0.6
0.5
0.5
0.4
0.4
0.3
0.3
0.2
0.2
0.1
0.1
0.1
0.2
0.3
0.4
0.5
0.6
0.7
Peak to Peak Throw (λ )
0.8
0.9
1
0
Figure 4.13: The contour plot of relative signal-to-noise ratio for Stokes Q, calculated
from equation 4.42 with linear chopping mode. This plot is for the 40 GHz band (33
GHz to 43 GHz, λ0 = 7.89 mm). The maximum is at (0.46 λ0 , 0.16 λ0 ) with the peak
signal-to-noise ratio scaled to be 1.00. There are 2 other local maxima nearby: (0.63
λ0 , 0.19 λ0 ) and (0.45 λ0 , 0.42 λ0 ). Details are listed in table 4.3.
87
Table 4.3: CLASS VPM Mirror Throw Optimization
Waveband
(GHz)
λ0
(mm)
33.0
43.0
7.890
77.3
108.3
3.231
126.8
164.3
2.060
Waveband
(GHz)
33.0
43.0
77.3
108.3
126.8
164.3
λ0
(mm)
7.890
3.231
2.060
Cosine chopping mode:
Maxima Relative SNR Throw Star-Pos Throw Star-Pos
(#)
(-)
(λ0 )
(λ0 )
(mm)
(mm)
1
1.000
0.19
0.13
1.500
1.026
2
0.942
0.19
0.39
1.500
3.077
3
0.912
0.44
0.13
3.472
1.026
4
0.861
0.44
0.39
3.472
3.077
5
0.849
0.27
0.26
2.130
2.051
1
1.000
0.19
0.13
0.614
0.420
2
0.907
0.19
0.39
0.614
1.260
3
0.892
0.44
0.13
1.422
0.420
4
0.838
0.27
0.25
0.872
0.808
5
0.811
0.44
0.39
1.422
1.260
1
1.000
0.19
0.13
0.391
0.268
2
0.944
0.19
0.40
0.391
0.824
3
0.912
0.45
0.13
0.927
0.268
4
0.862
0.45
0.39
0.927
0.803
5
0.849
0.28
0.26
0.577
0.536
Linear chopping mode:
Maxima Relative SNR Throw Star-Pos Throw Star-Pos
(#)
(-)
(λ0 )
(λ0 )
(mm)
(mm)
1
1.000
0.46
0.16
3.629
1.262
2
0.932
0.63
0.19
4.971
1.500
3
0.884
0.45
0.42
3.551
3.314
1
1.000
0.45
0.16
1.454
0.517
2
0.908
0.59
0.19
1.906
0.614
3
0.811
0.46
0.42
1.486
1.357
1
1.000
0.46
0.16
0.948
0.330
2
0.933
0.62
0.20
1.277
0.412
3
0.889
0.46
0.42
0.948
0.865
88
4.3.4
VPM Efficiency
This section is about VPM efficiency as a function of bandpass. To simplify the
calculation, we assume that the I, Q and V signal are constants in a given bandpass
and the VPM is operating at the best optimized chopping position with max signal
to noise ratio.
From section 4.3, the output power of the VPM can be written as:
Qcosφ + V sinφ + I
(4.44)
where Q and V are the Stokes parameters, I is the total intensity, and φ is the phase
delay in the VPM:
φ = kx = 2kdcos(θ)
(4.45)
where k is the wave number, x is the optical path difference, d is the grid-mirror
separation and θ = 20◦ is the angle of the incident radiation with the normal of the
VPM.
As an approximation, we assume the intensity and all the Stokes parameters,
are constants independent of frequency over the region of the passband. The TimeOrdered Data (TOD) from the experiment will be a function of time integrated over
the waveband:
1
T OD(t) =
φh − φl
Z
φh
(Qcosφ + V sinφ + I)dφ
(4.46)
φl
where, the indices l and h mean the lower and higher limit of the bandwidth: φl =
kl x = 2kl dcos(θ) and φh = kh x = 2kh dcos(θ) . In order to ignore the effects on photon
noise from changing the passband size, we normalize the TOD by the width of the
passband.
Instead of referring to the low and high values of the phase delay, we switch
coordinates to the geometric mean and ratios:
p
p
φ0 ≡ φl φh = x kl kh
r ≡ φh /φl
√
φl = φ0 / r
√
φh = φ0 r
89
(4.47)
where r > 1.0 is defined as the ratio of the upper to the lower frequency of the
bandwidth in this section (NOT the tensor-to-scalar ratio). Equation 4.46 can be
re-written as:
1
√
TOD(t) = √
φ0 r − φ0 / r
Z
√
φ0 r
√
φ0 / r
(Qcosφ + V sinφ + I)dφ
= Q × TODQ (t) + V × TODV (t) + I
where
√
√
√
r
[(sin(φ0 r) − sin(φ0 / r)]
φ0 (r − 1)
√
√
√
r
TODV (t) =
[(cos(φ0 / r) − cos(φ0 r)].
φ0 (r − 1)
TODQ (t) =
(4.48)
(4.49)
The shape of TODQ (t) and TODV (t) is dependent only on r. That is, one can
change φ0 , and then plot TODQ (t), but changing φ0 will only expand or contract the
horizontal direction, it won’t change the number of peaks within one period. As a
√
consequence, the VPM efficiency depends only on r, not on φ0 = x kl kh .
In order to solve for the Q, V , and I values, we can perform a linear least squares
analysis. Assuming white noise and that the error bar on each TOD measurement is
the same, then, equation 4.48 can be written as:
 
 
Q
Q
 
 

 
TODQ (t), TODV (t), 1 × 
V  = A × V  = TOD
I
I
then the least-squares solution is:
 
Q̂
 
V̂  = (AT A)−1 AT · TOD
 
Iˆ
√
Assuming a sinsoidal oscillation of φ0 (t) = x(t) kl kh with time:
p
p
p
φ0 (t) = xmin kl kh + (xmax kl kh − xmin kl kh )(cos(t) + 1)/2
(4.50)
(4.51)
(4.52)
where φ0 ranges from the first local minimum in TODQ to the next local maximum.
We take the integral over a half period of that oscillation to get:
90
T
(A A)QQ =
(AT A)QV = (AT A)V Q =
Z
Z0 π
0
T
T
(A A)QI = (A A)IQ =
Z
0
T
(A A)V V =
(AT A)V I = (AT A)IV =
Z
(A A)II =
Z
TOD2Q (t)dt
TODQ (t)TODV (t)dt
π
TODQ (t)dt
π
Z0 π
0
T
π
TOD2V (t)dt
TODV (t)dt
π
dt = π.
(4.53)
0
We then invert the AT A matrix to get the covariance matrix. To the extent that
AT A is a diagonal matrix, we have:
σQ = qR
π
1
TOD2Q (t)dt
0
.
(4.54)
From equation 4.49 and equation 4.54, we have σQ = σQ (r). We can define the
VPM efficiency as a function of the bandwidth (r):
η(r) = SNR(r)/SNR(r → 1.0) = σQ (r → 1.0)/σQ (r)
(4.55)
that is the signal-to-noise ratio of the bandwidth (r) normalized by the signal-tonoise ratio of a delta bandwidth (r → 1.0). Figure 4.14 shows the efficiency plot,
from r = 1.0 to r = 50.0.
4.3.5
Current Status
The prototype VPM grid was built [151] (figure 4.15) and measured [152]. It is
made of over 2 miles long, 63.5 µm (0.0025”) diameter, gold plated tungsten wires.
The wires were glued on an aluminium frame with a total of 2 tons stretching force.
This prototype grid has 2a/g = 1/3.15 ≈ 1/π, with 200 µm wire pitch. It has a 50 cm
diameter clear aperture, with flatness within 50 µm. The mechanical wire resonant
frequency is higher than 128 Hz.
91
VPM Efficiency
100
90
η (%)
80
70
60
50
40
30
5
10
15
20
25
r
30
35
40
45
50
Figure 4.14: VPM efficiency calculated from equation 4.55. The efficiency drops
quickly from r = 1.0 to r = 5.0 and becomes almost flat after r > 10. The noise at
large r is due to the rounding in the numerical calculations.
With a/λ0 ≈ 0.004, this wire grid can be considered as a perfect VPM grid for
the 40 GHz waveband. It should also have good performance for the 90 GHz band.
However, for the 150 GHz band, there will be significant difference between the VPM
grid reflection phase delay and the free-space grid-mirror delay (equation 4.27).
CLASS needs large aperture VPMs as the front-end modulators, i.e. the 40 GHz
band requires a 60 cm diameter VPM. Operating at room temperature, gold plated
tungsten wires are preferred because it provides adequate electrical conductivity and
high yield strength. The VPM mirror can be control by a Proportional-IntegralDerivative (PID) controller. Since the required mirror throw is short, a linear piezo
motor may be a good choice to drive the mirror.
4.4
CLASS Optics
Table 4.4 show the parameters of CLASS optics. The CLASS 40 GHz optics
design was completed [153]. The geometric parameters are: VPM diameter = 60.0
cm, effective focal length = 70.5 cm, f/2.0, focal plane diameter = 27.0 cm, Lyot stop
92
Figure 4.15: Photo of the prototype VPM grid. The wires are glued on an aluminium
box frame with over 2 tons of stretch force. The diameter of the flattener ring is 50 cm.
The wire diameter, 2a, is 63.5 µm, with wire pitch, g = 200 µm. 2a/g = 1/3.15 ≈ 1/π.
The flatness of the grid is better than 50 µm. The total length of the wires is longer
than 2 miles.
93
Table 4.4: CLASS Optics Overview
Waveband
40 GHz 90 GHz 150 GHz
◦
FOV ( )
18.0
7.0
3.5
Beamsize (◦ )
1.50
0.67
0.40
Strehl Ratio
> 0.995 > 0.990 > 0.990
f
2.0
2.0
2.0
# of detector pairs
36
150
60
diameter = 30.0 cm, FOV = 18.0◦ , number of pixels = 36. The 90 GHz and 150 GHz
optics will share a similar design as the 40 GHz band.
Figure 4.16 and figure 4.17 shows the drawings of CLASS 40 GHz optics and its
ray trace. It is a diffraction limited catadioptric system with fast speed, large FOV,
low cross-polarization and high Strehl ratio across the entire focal plane. It consists
of a front-end VPM, two mirrors, a vacuum window, a Lyot stop, two lenses and two
infrared (IR) blocking filters. The VPM and mirrors operate at room temperature,
while the lenses, filters and the focal plane are cooled by a cryostat.
The Point Spread Function (PSF) diagrams on the focal plane are shown in figure 4.18. The size of point spread is much smaller than the size first Airy disk (shown
as circles), showing a diffraction limited optics.
There are many methods to build the optical components by using different materials. The following are the tentative methods for CLASS: The cold lenses will
be made of high density polyethylene (HDPE) plastic, which is commonly used in
millimetre wavebands. The lenses can be anti-reflective (AR) coated by direct bonding of dielectric layers with the right thickness and index of refraction [154]. The IR
blocking filter can be made of polytetrafluoroethylene (PTFE). These filters have high
transmission for the wavelength longer than 60 µm [155], while absorb most of the
radiation with higher frequency. The 5 inch thick vacuum window can be constructed
by sandwiching 5 layers of the 1 inch thick Zotefoam (HD30).
94
600
40°
0
54.1°
182
1146.2
2200
1026
.5
1
94
0
50
7
12
ž
ž
ž
Figure 4.16: Top: Drawings of CLASS 40 GHz optics. It consists of a front-end
VPM, two mirrors, two lenses, a Lyot stop, a vacuum window and two infrared (IR)
blocking filters. Bottom: Drawing and the ray trace of the cooled optics. Units are
in mm. Figure courtesy of Joseph Eimer.
95
Figure 4.17: Ray trace of CLASS 40 GHz optics. Basic parameters: VPM diameter
= 60.0 cm, effective focal length = 70.5 cm, f/2.0, focal plane diameter = 27.0 cm,
Lyot stop diameter = 30.0 cm, FOV = 18.0◦ , number of pixels = 36. Figure courtesy
of Joseph Eimer.
96
Figure 4.18: Point spread diagram of CLASS 40 GHz optics from Zeemax. Each
diagram in this figure represents a separate direction on the sky. The circles show
the first Airy disk at the corresponding location. This diagram shows that the optics
is diffraction limited. Figure courtesy of Joseph Eimer.
97
4.5
Smooth-walled Feedhorn
CLASS requires feedhorns having symmetric beam patterns and low reflected
power over a large bandwidth. Conventional corrugated feedhorns can produce beam
patterns with low sidelobe levels, low cross polarization and low reflected power. However, corrugated feedhorns are difficult to manufacture and require high machining
precision. The cost of large arrays with hundreds of feedhorns is high, especially for
high frequency bands (i.e., CLASS 90 GHz and 150 GHz band).
As an alternative, smooth-walled feedhorns with monotonic profile are much more
straightforward to build. They can provide performance comparable to that of the
corrugated feedhorns. Smooth-walled feedhorns do not require high fabrication precision and are cost effective to build. A smooth-walled feed that has a 30% operational
bandwidth over which the cross-polarization response is better than -30 dB and reflected power is better than -28 dB was designed, built and measured [156]. This
smooth-walled feedhorn, however has relatively low aperture efficiency and high sidelobe levels due to its big aperture-to-length ratio. By reducing the aperture-to-length
ratio, a feedhorn with both cross polarization and return loss lower than -30 dB across
30% bandwidth was designed [157]. It provides a sidelobe level lower than -25 dB,
and an aperture efficiency of about 60%.
4.5.1
Smooth-walled Feedhorn Optimization
Input Waveguide
At the waveguide end of the of the horn, a short section of input circular waveguide
is included. The waveguide radius provides a homogeneous interface to a rectangular
waveguide by maintaining a uniform cutoff frequency across the discontinuity [158].
The cutoff frequency can be written as:
′
fc = c/(2ao ) = p11 c/(2πaguide )
(4.56)
where ao is the rectangular waveguide broadwall width, aguide is the circular waveguide
′
radius, and p11 ≈ 1.841 is the eigenvalue for T E11 mode, and c is the speed of light.
The cutoff wavelength is λc = c/fc .
98
Beam Calculation
The details of the feedhorn beam calculation technique can be found in [18] and
[156]. Basically, this method matches boundary conditions across adjacent concentric
cylindrical waveguide sections to determine the mode content at the aperture end of
the feedhorn based on a T E11 excitation at the circular waveguide end. The beam
pattern in the E- and H- planes is calculated directly from the modal content. The
full beam patterns can be calculated from the E- and H-plane profiles, since the horn
in this calculation is known to be a BOR1 antenna [159] from the symmetry of the
calculation.
The smooth-walled feedhorn is approximated by a profile that consists of discrete
cylindrical sections, each of constant radius. For this approximation to be valid,
the section length ∆l should be less than λc /20. It is also possible in principle to
dynamically set the length of each section to optimize the approximation to the local
curvature of the horn to increase the speed of the optimization.
Penalty Function
Generally, the smooth-walled feeds have good return loss performance [156]. It is
not necessary to include it in the penalty function. The penalty function is constructed
to depend on cross polarization and the edge taper at a give angle defined by the
optics. For the 40 GHz feedhorn, the bandwidth is from 33 GHz to 43 GHz, that is
1.25 fc to 1.63 fc (∆f /f0 = 26.3 %). The penalty function to minimize is
χ2 =
N X
M
X
i=1 j=1
αj ∆j (fi )2 ,
(4.57)
where i is the sum is over a discrete set of (N) frequencies in the optimization frequency band, and j sums over the number (M) of discrete parameters one wishes to
take into account for the optimization. The weights αj can be adjusted. In this work,
uniform weights (αj = 1) have been implemented. The CLASS feedhorn is optimized
by minimizing this penalty function including only the cross polarization and edge
taper (M = 2 in equation 4.57). Other parameters such as beam shape could also be
99
employed for different optimization requirements. The explicit forms used for ∆1 (f )
and ∆2 (f ) are
∆1 (f ) =
(
XP (f ) − XP0
0
∆2 (f ) = ET (f ) − ET0
if XP (f ) > XP0 ,
if XP (f ) ≤ XP0 ,
(4.58)
where XP (f ) is the maximum of the cross-polarization XP (f ) = Max[XP (f, θ)],
ET (f ) is the edge taper at a given angle at frequency f . Our target beam pattern
was for the D-plane to be -10 dB at the azimuth angle of 14◦ . Respectively, XP0 and
ET0 are the threshold cross polarization and edge taper level. If the cross polarization
or edge taper at a sampling frequency is less than or equal to its critical value, then
it does not contribute to the penalty function. Otherwise, its squared difference is
added to the penalty function.
Feedhorn Optimization
As shown in Figure 4.19, the feedhorn was optimized in a multi-step process that
employs a modified version of Powell’s method [160] at each step. Powell’s method
is a rapidly-converging method for finding the minima of a multi-variables function
without explicit analytical expression for its partial derivatives. In this method,
every variable of the function is free to float during the optimization. Generically,
this algorithm can produce an arbitrary profile. To produce a feed that is easily
machinable, we impose a restriction that the optimization is limited to the subset
of profiles for which the radius increases monotonically along the length of the horn.
Without this constraint, the serpentine profiles explored in [161] are accessible. Given
enough degrees of freedom, this method can recover the corrugated horn solution.
An initial input is required for the modified Powell method. A profile that is constructed by a sin0.75 converter section and a flare section that matches the expansion
of a Gaussian beam [162] is used for the initial profile. The feed radius, r, can be
written analytically as a function of the distance along the length of the horn z, as:
100
Feedhorn beam calculaon method from James
Inial input:
Sin0.75+Gaussian
add-on profile
Opmizaon
step 1:
5 points natural
spline profile
Opmizaon
step 2:
10 points natural
spline profile
Opmizaon
step 3:
20 points natural
spline profile
XP0=-25dB
ET0=-10 dB
XP0=-30dB
ET0=-10 dB
XP0=-34dB
ET0=-10 dB
Final profile
Figure 4.19: Flow chart of smooth-walled feedhorn optimization. Optimization begins
with a sin0.75 profile, the method from [18] is used to calculate the beam patterns.
The feedhorn profile was found by this multi-step iterative solution with different
thresholds in each step.
r(z) =
(
aguide + ac sin0.75 (πz/L)
if 0 ≤ z ≤ L/2,
aguide + ac {1 + [C(z − L/2)]2 }1/2 if L/2 < z ≤ L,
(4.59)
where
C = (2/L)[((af − aguide )/ac )2 − 1]1/2
(4.60)
ac is the radius at the end of the converter section, af is the final radius of the flare
section and L is the total length of the feedhorn. The initial profile of the CLASS
feedhorn has aguide = 0.293λc , ac = 0.650λc , af = 1.582λc and L = 8.789λc. This
profile is then approximated by natural spline of a set of 5 points. In the first step,
XP0 and ET0 are set to -25 dB and -10 dB. The minimum of the penalty function is
found by the modified Powell method in this 5-dimensional space. The output profile
from the first step is the initial input to the next optimization step.
In the following optimization steps, the number of points in the natural spline is
increased to be 10 and 20. The modified Powell’s method optimizes the profile in
10-dimensional and 20-dimensional spaces. Based on the result from the first step,
XP0 is set to be -30 dB and -34 dB for the 10-dimensional and 20-dimensional space.
ET0 remains unchanged in these steps.
In a previous work [156], a 560-points spline was used in the final optimization
101
Item
Waveguide
Bandwidth
Aperture
Length
Cross pol
Return loss
Edge taper
Table 4.5: CLASS 40 GHz Feedhorn Requirements
Requirement Note
3.334 mm
fc = 26.349 GHz, λc = 11.378 mm, WR 22.4
33 - 43 GHz 1.25 fc - 1.63 fc , ∆f /f0 = 26.3 %
36.00 mm
feedhorn wall thickness = 1.00 mm
100.00 mm D = 36.00 mm requires L ≥ 75 mm
≤ −30 dB
within 15◦ azimuth angle, across the bandwidth
≤ −30 dB
across the bandwidth
≈ −10 dB
at 14◦ , at center frequency (38 GHz)
step. The 20-point spline provided a sufficient number of degrees of freedom to achieve
the desire result since only small improvements are realized by doubling the number
of points from 10 to 20 and starting with the 5-point spline did produce the general
features of the final horn, and significantly reduces the time required by the slower
10-point and 20-point algorithm.
4.5.2
Smooth-walled Feedhorn for CLASS
Table 4.5 lists the requirements for optimizing the CLASS 40 GHz band feedhorn.
The feedhorn is optimized in the bandwidth of 33 GHz to 43 GHz (section 4.2.2). The
input waveguide has a radius of 3.334 mm, with fc = 26.349 GHz, λc = 11.378 mm
(equation 4.56). The packing pattern of the feedhorn array and the size of the focal
plane set a limit of 38.00 mm on the outer diameter of each feedhorn. The optical
design specifies about a -10 dB edge taper at a 14◦ angle on the VPM. The beam
at the angle greater than that will be terminated. The cross polarization should be
lower than -30 dB within this angle and across the entire bandwidth and the return
loss should be always lower than -30 dB.
Figure 4.20 shows the feedhorn profile. A 20-point approximation of this profile
is listed in table 4.6. A 500 point table can be found in appendix E. The final profile
has aguide = 0.293λc , ac = 0.853λc , af = 1.574λc and L = 8.789λc.
Table 4.7 and figure 4.21 shows the cross polarization, return loss and edge from
30 to 50 GHz. The cross polarization at the trough near the center frequency is about
102
Smooth−walled Feedhorn Profile
Radius (mm)
20
10
0
−10
−20
−10
0
10
20
30
40
50
Length (mm)
60
70
80
90
100
Figure 4.20: CLASS 40 GHz feedhorn profile. The 10.00 mm long input waveguide
has a radius of 3.334 mm, with fc = 26.349 GHz. The length of the feedhorn is
100.00 mm. The aperture is 35.828 mm. This is a monotonic profile that allows a
progressive milling technique.
Cross−Pol, Return−Loss and Edge−Taper
−10
−20
Cross−Pol
Return−Loss
Edge−Taper
Power (dB)
−30
−40
−50
−60
−70
1.1 1.15 1.2 1.25 1.3 1.35 1.4 1.45 1.5 1.55 1.6 1.65 1.7 1.75 1.8 1.85 1.9
Freqency (fc)
Figure 4.21: CLASS feedhorn performance from 30 to 50 GHz. The dashed lines
define the -30 dB line, and the waveband limit of 33 GHz and 43 GHz. The cut off
frequency is fc = 26.349 GHz.
103
Table 4.6: Feedhorn Profile Approximation (in Millimeters)
Step
Length (z)
Radius (r)
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
0.00
5.00
10.00
15.00
20.00
25.00
30.00
35.00
40.00
45.00
50.00
55.00
60.00
65.00
70.00
75.00
80.00
85.00
90.00
95.00
100.00
3.334
4.555
5.749
6.882
7.906
8.755
9.330
9.578
9.672
9.776
9.811
9.836
9.866
11.042
12.919
15.010
16.718
17.577
17.838
17.892
17.914
-40 dB and about -30 dB at the edges of the bandwidth. The cross polarization is
below -30 dB in entire Q band (33 - 45 GHz), which is better than the requirement
(table 4.5). The return loss is about -30 dB at the low frequency edge and drops
below -40 dB at high frequencies. The edge taper is about -10.8 dB at 38 GHz, and
rise slowly towards the edges of the bandwidth. For a feedhorn with a perfect beam
pattern and zero cross polarization, the edge taper at a given angle should decrease as
the frequency increases (a wavelength effect). The edge taper in our penalty function
is defined as the power of the diagonal plane (the average of the E- and H- plane) at
14◦ . From the low to high frequency edges, the power levels of the E- and H-plane
flip (see figure 4.24 and figure 4.25, at 33 GHz, E-plane < H-plane, while E-plane
104
Table 4.7: Feedhorn Performance
f
[GHz]
f
[fc ]
λ
[mm]
Cross Pol
[dB within 15◦ ]
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
1.139
1.177
1.214
1.252
1.290
1.328
1.366
1.404
1.442
1.480
1.518
1.556
1.594
1.632
1.670
1.708
1.746
1.784
1.822
1.860
1.898
9.993
9.671
8.369
9.085
8.817
8.565
8.328
8.102
7.889
7.687
7.495
7.312
7.138
6.972
6.813
6.662
6.517
6.379
6.246
6.118
5.996
-22.77
-25.00
-26.71
-30.01
-31.26
-33.74
-34.30
-39.62
-39.00
-36.51
-35.75
-34.83
-32.49
-32.17
-30.21
-29.11
-27.85
-26.40
-25.57
-24.11
-23.57
Return Loss Edge Taper
[dB]
[dB at 14◦ ]
-21.80
-24.11
-27.95
-30.09
-32.89
-37.01
-36.99
-45.20
-39.86
-59.07
-41.55
-64.50
-41.61
-49.95
-42.31
-43.99
-44.88
-41.39
-51.60
-40.68
-51.10
-7.65
-7.95
-8.32
-8.69
-9.20
-9.63
-10.05
-10.45
-10.80
-11.45
-11.65
-11.79
-11.88
-11.68
-11.57
-11.42
-11.15
-11.13
-10.84
-10.99
-10.75
> H-plane at 44 GHz), while their average value (diagonal plane) remains the same,
ending up with higher edge tapers at frequency edges (an average effect). From 30
to 42 GHz, where the wavelength effect dominates, the edge taper drops. At higher
frequency, where the average effect dominates, the edge taper increases with a slow
rate.
Figure 4.22 and figure 4.23 show the beam pattern within a ±90◦ angle from 33
to 44 GHz. The sidelobe level of this feedhorn is about -15 dB. The FWHM at the
center frequency is about 14.6◦. The penalty function only takes the beam within 14◦
into account. Figure 4.24 and figure 4.25 show the beam pattern zoomed in to within
15◦ .
105
33GHz HWHM=8.37deg
-20
-40
0
Power (dB)
E Plane
H Plane
D Plane
X Pol
0
Power (dB)
34GHz HWHM=8.12deg
-60
-90 -70 -50 -30 -10 10 30 50 70 90
Angle (degrees)
-20
-40
-60
-90 -70 -50 -30 -10 10 30 50 70 90
Angle (degrees)
35GHz HWHM=7.93deg
36GHz HWHM=7.72deg
0
Power (dB)
Power (dB)
0
-20
-40
-60
-90 -70 -50 -30 -10 10 30 50 70 90
Angle (degrees)
-20
-40
-60
-90 -70 -50 -30 -10 10 30 50 70 90
Angle (degrees)
37GHz HWHM=7.55deg
38GHz HWHM=7.33deg
-20
-40
0
Power (dB)
Power (dB)
0
-60
-90 -70 -50 -30 -10 10 30 50 70 90
Angle (degrees)
-20
-40
-60
-90 -70 -50 -30 -10 10 30 50 70 90
Angle (degrees)
Figure 4.22: Beam patterns of the CLASS smooth-walled feedhorn within azimuth
angles of ±90◦ , from 33 GHz to 38 GHz.
106
39GHz HWHM=7.10deg
E Plane
H Plane
D Plane
X Pol
-20
-40
0
Power (dB)
Power (dB)
0
40GHz HWHM=6.92deg
-60
-90 -70 -50 -30 -10 10 30 50 70 90
Angle (degrees)
-20
-40
-60
-90 -70 -50 -30 -10 10 30 50 70 90
Angle (degrees)
41GHz HWHM=6.73deg
42GHz HWHM=6.55deg
0
Power (dB)
Power (dB)
0
-20
-40
-60
-90 -70 -50 -30 -10 10 30 50 70 90
Angle (degrees)
-20
-40
-60
-90 -70 -50 -30 -10 10 30 50 70 90
Angle (degrees)
43GHz HWHM=6.42deg
44GHz HWHM=6.26deg
-20
-40
0
Power (dB)
Power (dB)
0
-60
-90 -70 -50 -30 -10 10 30 50 70 90
Angle (degrees)
-20
-40
-60
-90 -70 -50 -30 -10 10 30 50 70 90
Angle (degrees)
Figure 4.23: Beam patterns of the CLASS smooth-walled feedhorn within azimuth
angles of ±90◦ , from 39 GHz to 44 GHz.
107
33GHz HWHM=8.37deg
34GHz HWHM=8.12deg
-20
0
E Plane
H Plane
D Plane
X Pol
-40
Power (dB)
Power (dB)
0
-60
-15 -12 -9 -6 -3 0 3 6 9 12 15
Angle (degrees)
-20
-40
-60
-15 -12 -9 -6 -3 0 3 6 9 12 15
Angle (degrees)
35GHz HWHM=7.93deg
36GHz HWHM=7.72deg
0
Power (dB)
Power (dB)
0
-20
-40
-60
-15 -12 -9 -6 -3 0 3 6 9 12 15
Angle (degrees)
-20
-40
-60
-15 -12 -9 -6 -3 0 3 6 9 12 15
Angle (degrees)
37GHz HWHM=7.55deg
38GHz HWHM=7.33deg
-20
-40
0
Power (dB)
Power (dB)
0
-60
-15 -12 -9 -6 -3 0 3 6 9 12 15
Angle (degrees)
-20
-40
-60
-15 -12 -9 -6 -3 0 3 6 9 12 15
Angle (degrees)
Figure 4.24: Beam patterns of the CLASS smooth-walled feedhorn within azimuth
angles of ±15◦ , from 33 GHz to 38 GHz.
108
39GHz HWHM=7.10deg
40GHz HWHM=6.92deg
-20
0
E Plane
H Plane
D Plane
X Pol
-40
Power (dB)
Power (dB)
0
-60
-15 -12 -9 -6 -3 0 3 6 9 12 15
Angle (degrees)
-20
-40
-60
-15 -12 -9 -6 -3 0 3 6 9 12 15
Angle (degrees)
41GHz HWHM=6.73deg
42GHz HWHM=6.55deg
0
Power (dB)
Power (dB)
0
-20
-40
-60
-15 -12 -9 -6 -3 0 3 6 9 12 15
Angle (degrees)
-20
-40
-60
-15 -12 -9 -6 -3 0 3 6 9 12 15
Angle (degrees)
43GHz HWHM=6.42deg
44GHz HWHM=6.26deg
-20
-40
0
Power (dB)
Power (dB)
0
-60
-15 -12 -9 -6 -3 0 3 6 9 12 15
Angle (degrees)
-20
-40
-60
-15 -12 -9 -6 -3 0 3 6 9 12 15
Angle (degrees)
Figure 4.25: Beam patterns of the CLASS smooth-walled feedhorn within azimuth
angles of ±15◦ , from 39 GHz to 44 GHz.
109
Table 4.8: Beam Parameters
f
[-]
[GHz]
λ
[-]
[mm]
Beam Solid
Angle
[Sr]
Antenna
Gain
[dBi]
Aperture
Efficiency
[-]
Main Beam
Efficiency
[within 14◦ ]
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
9.993
9.671
9.369
9.085
8.817
8.565
8.328
8.102
7.889
7.687
7.495
7.312
7.138
6.972
6.813
6.662
6.517
6.379
6.246
6.118
5.996
0.131
0.126
0.121
0.115
0.109
0.105
0.100
0.095
0.092
0.087
0.083
0.081
0.078
0.076
0.074
0.072
0.070
0.068
0.067
0.065
0.065
19.81
20.00
20.18
20.41
20.63
20.80
20.99
21.22
21.36
21.61
21.79
21.91
22.09
22.18
22.33
22.44
22.54
22.66
22.71
22.85
22.87
0.741
0.725
0.709
0.702
0.697
0.683
0.675
0.674
0.660
0.664
0.658
0.643
0.639
0.622
0.615
0.603
0.590
0.582
0.565
0.559
0.541
0.914
0.927
0.936
0.946
0.953
0.958
0.966
0.974
0.977
0.979
0.979
0.977
0.975
0.973
0.971
0.970
0.968
0.968
0.966
0.966
0.967
The beam parameters are shown in table 4.8. The antenna gain is at the level
of about 21 dBi, aperture efficiency is about 67% and the main beam (within 14◦ )
efficiency is above 95%.
A tolerance study was conducted based on the averaged values of cross polarization, return loss and edge taper across the waveband. In the tolerance study, the
tolerance (the x axis of figure 4.26) is the amplitude of the Gaussian random noise
applied to the radius of feedhorn profile. For each tolerance between 0 and 300 µm,
these average values were calculated 120 times and then averaged. By taking the
average value of cross polarization = -30 dB as the criterion, then this Q band feed110
$YHUDJHG&URVV3RO5HWXUHQ/RVVDQG(GJH7DSHU
&URVV3RO
5HWXUQ/RVV
(GJH7DSHU
3RZHUG%
7ROHUDQFHXP
Figure 4.26: The averaged cross-pol, return-loss and edge-taper plot for the tolerance
calculation from 0 to 300 um. For each tolerance, these values were from the average
of 120 calculations. (The plots are noisy at large tolerance, more calculation would
be required to smooth the plots.)
horn has a fabrication tolerance at 1σ level of about 250 µm (0.010 inch). With a
machining tolerance of 25 µm (0.001 inch), this design can be scaled up to 400 GHz.
4.6
4.6.1
CLASS Detectors
Focal Plane
The focal planes of CLASS (figure 4.27) consist of feedhorn-coupled, TES bolometers. The smooth-walled feedhorn provides well-controlled symmetric angular beam
pattern through the optics (see section 4.5). A symmetric planar orthomode transducer (OMT) with the horizontal (H) and vertical (V ) probe antennas is utilized
to couple the orthogonal linear polarizations at feedhorn throat into independent
111
Figure 4.27: Section view of CLASS 40 GHz focal plane. It consists of a array of
36 smooth-walled feedhorns, waveguide adapter, detector mounting plate and clips.
The focal plane will operate at a temperature of 100 mK. Figure courtesy of Thomas
Essinger-Hileman.
superconducting microstrip transmission lines. Band-defining filters limit the spectral range for each of the H and V polarizations. The signals terminate in resistors
thermally coupled to TESs that are capable of providing background-limited performance. A λ/4 backshort is positioned behind the OMT to maximize the power from
the waveguide to the microstrip lines (figure 4.28).
The CLASS 40 and 90 GHz detectors are designed by the Goddard Space Flight
Center (GSFC) and the 150 GHz detectors are design by National Institute of Standards and Technology (NIST). In the GSFC design, broadband hybrid couplers
(Magic Tees) combine the signals from opposite antennas and outputs the difference
between these signals. For the 150 GHz channel, the signals from opposite antennas
112
Figure 4.28: The feedhorn-couple TES bolometers set up [15] and prototype detector
chip for the 40 GHz CLASS [19]. Left: The detector set up showing the feedhorn,
detector housing, detector chip and backshort. Right: Photo of a 40 GHz prototype
detector chip, showing the OMT, Magic Tees, filters and TES membranes.
share a thermal coupling to the same TES.
4.6.2
TES Bolometers
A TES consists of a superconducting film operated in the narrow temperature
region between the normal and superconducting state, where the electrical resistance
varies between zero and its normal value. In this state, the device has a finite electrical
resistance, R, that is less than the resistance in the fully non-superconducting state,
Rn . Energy (Pγ ) coupled to the detector increases its temperature, pushing it further
into the non-superconducting state and thereby increasing its electrical resistance.
This increase in resistance can be used to detect very small changes in temperature,
and hence in energy [20].
Figure 4.29 shows the electro-thermal circuit diagram of a TES bolometer. In this
simplest model, the bolometer has a heat capacity C at temperature T , which is linked
to the thermal bath with temperature Tbath (T > Tbath ) by a thermal conductance G.
The bolometer is heated up by the absorbed radiation Pγ and the Joule power PJ ,
and power PG is conducted away through the weak link:
113
Figure 4.29: The electro-thermal circuit diagram of a TES bolometer (modified from
[20]). Left: Each pix with a heat capacity of C at temperature T is connected by
a thermal link G to a thermal source with a temperature of Tbath . The total power
to the pixel is Pγ + PJ − PG . Right: TES is biased by IB = VB /RB , in the case
of RB ≫ RSH . For R ≫ RSH , the TES is bias by V = IB RSH , then fluctuations of
R will result in fluctuation in current, which is read out by the inductor L and the
superconducting quantum interference device (SQUID) amplifier.
114
C
dT
= Pγ + PJ − PG
dt
(4.61)
where
PJ = I 2 R
(4.62)
is the power dissipated when bias the TES with current I, and
Z T
PG =
G(T )dT.
(4.63)
Tbath
The electrical circuit in the right panel of figure 4.29 can be written as:
L
dI
+ IR = (IB − I)RSH
dt
(4.64)
where I is the current running through TES.
Operating at equilibrium (dT /dt = 0 and dI/dt = 0), the saturation power of a
TES bolometer can be written as
Psat = PG −
2
Imin
Rn
= PG −
IB RSH
RSH + Rn
2
Rn
(4.65)
where, Rn and Imin are the resistance and the current running through TES at normal
state. In the limit of a voltage bias (Rn ≫ RSH ), and a narrow transition, so that
PG ≈ V 2 /Ro is approximately constant at equilibrium, equation 4.65 reduces to
Psat = (1 − Ro /Rn )PG
(4.66)
where, Ro is the resistance of the TES at equilibrium (operating point).
The total NEP of a TES can be written as:
NEP = (NEP2det + NEP2γ )1/2 ≈ (4kB Go To2 + 2Pγ hν)1/2
(4.67)
where NEPdet is the NEP due to phonons noise in the detector, NEPγ is due to
fuctuations in the radiation load from sky background. Go and To are thermal conductance and temperature of the TES at the equilibrium point. CLASS detectors
are background limited, that is NEPdet is smaller than NEPγ from the background
radiation.
115
A TES bolometer loses all sensitivity when the signal power exceeds Psat . To
maximize the TES performance, the thermal conductance, Go , must be chosen to be
large enough that any important signal does not saturate the bolometer. Increasing
Go so that the highest signal power does not saturate, however, degrades the NEP for
even the lowest measured signal power. The requirement of CLASS 40 GHz detectors
is : Psat = 3.5 pW, Go = 116 pW/K, To = 0.150 K and NEPdet = 1.2 × 10−17
WHz−1/2 .
4.7
4.7.1
Lab Set up for Detector Testing
Cryostat
The cryostat for CLASS detector testing in the experimental cosmology lab at
Johns Hopkins University is a model 104 Olympus pulse tube (PT) cryostat manufactured by the High Precision Devices (HPD) Inc. A Helium-4 (He-4) refrigerator
and an adiabatic demagnetization refrigerator (ADR) are mounted on the 4 K plate
of the cryostat. The He-4 refrigerator is launched from the 4 K plate with a base
temperature of 2.7 K, while the ADR can be launched from 4 K plate or the He-4
head with a base temperature of about 660 mK.
Figure 4.30 shows the section view of the lab cryostat. It is a two-stage PT
cryostat, with cooling power of 40 W at 45 K (1st stage, 60 K plate) and 1.5 W at 4.2
K (2nd stage, 4 K plate). On the 4 K plate, there is a two stage ADR system with
a gadolinium gallium garnet (GGG) crystal and a ferric ammonium alum (FAA) salt
pill. Each pill has its own ultra low thermal conducting support structure isolating it
from the 4 K flange and the intermediate stage. The two stages operate at a typical
temperature of ∼1 K (GGG) and ∼100 mK (FAA) with the cooling capacity of 1.2 J
(GGG) and 118 mJ (FAA). A He-4 refrigerator with ∼ 80 J cooling capacity at 660
mK can be mounted on the 4 K plate optionally (left panel of figure 4.31).
116
Figure 4.30: Section view of model 104 Olympus ADR cryostat showing mechanical
heat switch controller, vacuum valve, pulse tube (PT) head, 60 K plate, 4 K plate,
adiabatic demagnetization refrigerator (ADR), high temp superconducting leads for
4 T magnet, thermal shielding, and vacuum jacket [21].
117
4.7.2
Thermometry
The thermometry of the lab cryostat includes a general thermometer readout
system and an ADR Proportional-Integral-Derivative (PID) control system. The
general sensor readout system consists of a Stanford Research Systems (SRS) SIM900
mainframe with GPIB port, two SIM925 octal four-wire multiplexers (MUXs), a
SIM922 diode temperature monitor and a SIM921 AC resistance bridge. MUX 1
is for reading out silicon diodes and MUX 2 is for reading out ruthenium oxide
(RuOx) and other resistance temperature detectors (RTDs). The ADR PID control
system includes a Lakeshore model 370 AC resistance bridge, a calibrated GR-50-AA
germanium resistance temperature (GRT) sensor (mounted inside the cryostat) and
two Keithley model 2440 5 A sourcemeters. The above devices communicate with
a cryostat computer through a National Instruments (NI) model GPIB-ENET/100
GPIB to Ethernet adapter (right panel of figure 4.31). The mechanical heat switch
of the ADR is controlled via a NI USB-6009 Data Acquisition (DAQ) device.
The thermometry is control by LabVIEW programs (see appendix F for details).
For general thermometer readout, the program loops over the two octal MUXs to
produce real time plots. In the mean time, it also displays and saves all data with
time stamps. The readout process is in series. Due to the delay in each readout
caused by the response time of the diode monitor and the AC resistance bridge, it
take about 120 seconds to finish a single loop for reading out all channels of two
MUXs. To regulate the ADR temperature, the PID program reads the temperature
from the GRT sensor through the Lakeshore AC resistance bridge, calculates the
output to the Keithley current source by the PID algorithm, and controls the current
in the ADR magnet. This program also produces real time plots of the temperature
and error between the temperature and the set point. The temperature and the
magnet current are saved with time stamps in a file.
4.7.3
Cryostat Performance
Figure 4.32 shows the cool down curves of the cryostat from warm temperature
(∼ 300 K) to cool temperature (equilibrium temperature). It takes about 24 hours
118
Figure 4.31: Left: The ADR and the He-4 refrigerator mounted on the 4 K plate of the
HPD cryostat in the experimental cosmology lab at Johns Hopkins University. Photo
courtesy of David Larson. Right: the rack-mounted devices for cryostat thermometry.
From top to bottom, they are, a SRS SIM900 mainframe with 2 MUXs, a diode
moniter and an AC bridge, a front panel, a NI GPIB to Ethernet adapter, a Lakeshore
370 AC resistance bridge and two Keithley 2440 current sources.
for the cryostat to cool down to the state with stable temperature readouts. The
typical values of the thermometers are listed in table 4.9. The 60 K plate can reach
the temperature of 50.0 K and the 4 K plate can get as lower as 2.7 K.
Launching from the 4 K plate with a 2.7 K base temperature, the ADR can last
for about 210 hour at 100 mK with no load (FAA pill). Thus, the intrinsic thermal
load of the FAA pill is around 0.15 µW. Figure 4.33 shows the cooling curves (the
magnet current versus time) of the ADR with the loads of from 2.0 to 10.0 µW.
Based on these curves, the FAA pill of the ADR have higher cooling capacities at
lower loads. With a 2 µW load, the cooling capacity is about 130 mJ, which is close
to the theoretical number of 118 mJ. While with a 10 µW load, the capacity drops
to about 50 mJ.
4.7.4
Detector Readout
The signal from the TES bolometers is read out by two stages of the superconducting quantum interference device (SQUID) amplifier. The output of the SQUID
amplifier is a voltage that is approximately a sinusoidal function of the magnetic flux
119
&U\RVWDW&RRO'RZQFXUYHV
.SXOVHWXEH
.SXOVHWXEH
.SODWH
.SODWH
$'5PDJQHW
7HPSHUDWXUH.
7LPH+U
Figure 4.32: Cryostat cool down curves. It takes about 24 hours for the cryostat to
cool down to the state with stable temperature readouts. The typical values of the
thermometers are listed in table 4.9.
120
$'5FRROLQJFXUYHV#P.
X:
X:
X:
X:
X:
&XUUHQW$
7LPH+U
Figure 4.33: ADR cooling curves at 100 mK, showing the magnet current versus time
of the ADR with the loads of from 2.0 to 10.0 µW. Based on these curves, the FAA
pill of the ADR have higher cooling capacities at lower loads.
121
Thermometer
Diode
Magnet
4 K plate
60 K plate
60 K PT
4 K PT
He4 HS
He4 Charcoal
RTD
50 mK Ruox
1 K Ruox
Magnet RTD
R1
R2
R3
Table 4.9: Cryostat Thermometry Readout
Make
Model
Warm readout
[-]
[-]
[K]
[V]
Lakeshore
DT670
294.6 0.5720
Lakeshore
DT670
293.8 0.5739
Lakeshore
DT670
293.9 0.5738
Lakeshore
DT670
294.1 0.5732
Lakeshore
DT670
295.1 0.5709
Unknow
Unknow 300.0 0.5684
Lakeshore
DT670
293.4 0.5749
[-]
[-]
[K]
[kΩ]
Scientific Inst
RO600
265.8 1.003
Scientific Inst
RO600
281.8 1.002
AMI
Unknow 293.0 0.1047
Lakeshore
RX-202A 115.0 2.000
Lakeshore
RX-202A 109.1 2.011
Lakeshore
RX-102A 216.1 1.003
Cool readout
[K]
[V]
2.701 1.619
2.722 1.619
50.28 1.073
35.94 1.097
2.745 1.618
2.310 1.142
2.937 1.614
[K]
[kΩ]
2.821 1.551
2.828 1.550
2.641 2.452
2.918 3.146
2.912 3.147
2.725 1.548
φ through the SQUID junction loop [163]:
V = (R/2)(I 2 − (2Ic cos(πφ/φ0 ))2 )1/2 ,
(4.68)
where R is the resistance of the Josephson junctions, I is the SQUID bias current, Ic
is the Josephson junction critical current, and φ0 is the magnetic flux quantum: φ0
= h/2e = 2.07 × 10−15 Wb.
As shown in the left panel of figure 4.34 (Cold Electronics), fluctuations in the TES
current generate fluctuations in the flux of SQUID 1 (SQ 1), which is coupled to SQ
2 and then the SQUID Series Array (SSA). A flux-locked loop (FLL) is used to keep
the system response linear, that is, the resulting change in SQUID voltage is a linear
function of flux φ. The voltage output of the SSA (SSA SIG) is input to a differencing
amplifier of which the other input is wired to a fixed voltage (SA OFFSET). Then,
the output of this amplifier drives a feedback coil (Lfb ), for coupling magnetic flux
back to SQ 1. With the FLL, a fluctuation in current from the TES results in a
fluctuation on the feedback coil, Lfb , which cancels the flux from the input.
To read out numbers of TES bolometers on a focal plane, the In-focal-plane
SQUID multiplexers (MUXs) have been developed [164]. The TESs and SQUIDs
122
Cold Electronics
Warm Electronics
(MCE)
Ibias
TES Bias
Rshunt
14b
D/A
SQ1_FB
÷2n
Data Mode 2
LPF
RTES
SA_BIAS
I
÷2m
Lfb
Data Mode 1
15 k
Lin
PID
SSA_SIG
SQ1
(110
)
A=195
A/D
14b +
-
Data Mode 0
-
SQ2
ADC_OFFSET
0.1
Data Mode 3
SA_OFFSET
(110
)
SA_FB
SQ2_BIAS (SB)
SQ2_FB
SQ1_BIAS (RS)
Figure 4.34: The FLL block diagram for TES detector readout, showing the cold
electronics inside the cryostat and the warm electronics (MCE) [22].
are operated at cold temperature in the cryostat (left panel of figure 4.34). The
Multi-Channel Electronics (MCE), which controls the bias setting and the FFL feedback control (warm electronics) is mounted on the wall of the cryostat with magnetic
shielding (right panel of figure 4.34). The MCE is provided by the University of
British Columbia (UBC).
Figure 4.35 shows a photo of the MCE at Johns Hopkins University. The MCE
controls the SQUID amplifiers and MUXs, and reads signals from the TES array.
Each box of the MCE is in turn connected by fiber optic cables to data-acquisition
computers running real-time Linux and data-acquisition software (DAS).
123
Figure 4.35: This photo shows the Multi-Channel Electronics (MCE) mounted on
the wall the cryostat in the experimental cosmology lab at Johns Hopkins University.
The MCE is connected to a data-acquisition computer by a pair of fiber optic cables
(the orange wires). Photo courtesy of David Larson.
124
Appendix A
M17 Polarization Data
A.1
Polarziation Spectrum: 450 um vs 60 um
∆α1
80.0
70.1
62.7
60.3
57.8
50.4
42.9
38.0
33.0
30.6
28.1
23.1
13.2
∆δ 1 P450
44.0 2.2
-3.5 1.5
17.9 1.8
-51.0 2.5
39.2 2.0
60.6 2.4
13.1 1.1
-58.1 2.1
-36.8 1.4
53.5 1.6
-15.4 1.4
77.2 1.6
-41.5 1.5
σp P.A.2
0.5 18.5
0.3 21.9
0.2 17.6
0.4 38.2
0.2 15.4
0.3 23.4
0.2 7.3
0.2 40.6
0.2 33.0
0.2 19.7
0.1 12.7
0.2 20.4
0.1 26.4
σP.A.
5.9
5.2
3.8
4.2
3.4
3.0
4.3
2.7
3.0
2.9
2.6
3.2
2.2
P60
6.7
4.5
4.5
4.8
5.3
5.7
2.8
5.2
4.7
3.8
3.7
3.4
3.8
σp P.A.2
0.5 21.7
0.3 23.0
0.2 22.8
0.5 33.6
0.2 20.6
0.3 26.0
0.2 14.3
0.4 43.5
0.3 28.8
0.2 15.8
0.2 17.9
0.5 21.3
0.3 34.4
Offsets in arcseconds from 18h 17m 32s ,-16◦14′ 50′′ (B1950.0).
2
Position angle of E vector east from north.
3
Median = 0.390, mean = 0.395 and std = 0.056.
1
125
σP.A.
2.2
1.6
1.4
2.8
1.3
1.7
1.8
2.1
1.7
1.9
1.6
3.7
2.0
P450 /P60 3
0.33
0.33
0.40
0.52
0.38
0.42
0.39
0.40
0.30
0.42
0.38
0.47
0.39
Figure A.1: 60 um polarization vectors from Stokes ([23], Yellow) and the 450 um
result from SHARP (smoothed to 22′′ resolution, Red), center at 18h 17m 32s ,-16◦14′ 25′′
(B1950.0).
126
A.2
Polarziation Spectrum: 450 um vs 100 um
∆α1
119.9
110.0
100.1
92.7
90.2
85.3
80.3
63.0
55.6
45.7
38.3
∆δ 1 P450
-160.4 3.0
-124.8 1.4
-89.1 1.6
-205.5 1.5
-51.1 2.2
-169.9 2.0
-17.9 1.7
-98.6 1.2
-63.0 1.3
-25.0 1.5
-143.8 1.4
σp P.A.2
0.5 36.9
0.2 30.7
0.2 16.1
0.3 50.5
0.2 22.0
0.2 41.4
0.2 28.6
0.1
5.7
0.1
9.8
0.1 17.2
0.1 11.4
σP.A.
4.7
4.4
3.0
6.1
2.4
2.7
3.6
1.9
1.9
1.8
1.4
P100
3.9
4.4
3.8
3.5
4.2
3.5
3.4
2.3
2.8
2.0
2.7
σp P.A.2
0.3 27.5
0.2 23.0
0.3 20.4
0.3 51.9
0.3 26.3
0.2 35.5
0.4 34.7
0.2 10.1
0.2 13.2
0.1 25.5
0.3 21.3
Offsets in arcseconds from 18h 17m 30s ,-16◦13′ 03′′ (B1950.0).
Position angle of E vector east from north.
3
Median = 0.520, mean = 0.525 and std = 0.128.
1
2
127
σP.A.
2.3
1.6
2.2
2.9
2.0
1.9
3.1
1.8
2.4
1.9
3.0
P450 /P100 3
0.77
0.32
0.42
0.43
0.52
0.57
0.50
0.52
0.46
0.75
0.52
Figure A.2: 100 um polarization vectors from Stokes ([23], Green) and the 450um
result from SHARP (smoothed to 35′′ resolution, Red), center at 18h 17m 32s ,-16◦14′ 25′′
(B1950.0).
128
A.3
Polarziation Spectrum: 450 um vs 350 um at
RA > 18h17m30s
∆α1
71.7
61.8
59.4
56.9
54.4
51.9
44.5
42.0
39.6
37.1
34.6
32.1
29.7
27.2
24.7
22.2
19.8
17.3
14.8
12.4
9.9
4.9
∆δ 1 P450
-54.6 1.6
-19.0 1.1
-76.0 2.1
-2.4 1.4
71.2 1.8
14.2 1.6
-23.8 1.1
49.9 1.7
-7.1 1.3
66.5 1.7
9.5
1.3
-45.1 1.4
26.1 1.3
-28.5 1.8
-85.5 2.2
-11.9 1.5
61.7 1.7
4.7
1.4
-49.9 1.7
21.4 1.1
-33.3 2.2
-16.6 1.8
σp
0.3
0.2
0.3
0.2
0.4
0.2
0.2
0.2
0.2
0.3
0.1
0.1
0.1
0.1
0.2
0.1
0.2
0.1
0.1
0.1
0.1
0.1
P.A.2
35.4
20.4
40.2
5.9
30.1
9.7
15.3
22.0
2.4
21.9
2.8
12.0
17.7
-0.1
35.2
1.3
19.3
0.5
-0.9
4.6
-7.8
-9.7
σP.A.
5.4
4.9
4.2
3.7
6.5
3.3
4.1
3.8
3.3
4.3
3.2
2.3
3.2
1.9
2.4
2.0
2.7
2.2
1.5
3.1
1.1
1.1
P350
2.0
1.5
2.3
2.3
2.3
2.0
2.0
1.3
2.0
1.2
2.2
1.9
1.8
2.2
1.7
2.1
1.0
2.0
1.8
1.4
2.1
2.0
σp P.A.2
0.2 27.8
0.1 13.1
0.3 35.1
0.1 4.5
0.4 24.5
0.2 7.3
0.1 5.9
0.2 15.0
0.1 3.0
0.2 17.2
0.1 5.0
0.1 6.7
0.1 7.9
0.1 180.0
0.2 30.9
0.1 178.7
0.1 14.6
0.0 177.7
0.1 178.6
0.1 177.3
0.1 177.1
0.0 173.2
Offsets in arcseconds from 18h 17m 31.4s ,-16◦ 14′ 25′′ (B1950.0).
2
Position angle of E vector east from north.
3
Median = 0.795, mean = 0.887 and std = 0.289.
1
129
σP.A.
3.5
2.6
3.7
1.7
5.1
2.9
1.2
3.9
1.0
4.6
1.0
0.9
1.3
0.6
3.4
0.7
3.4
0.6
0.8
1.1
0.6
0.5
P450 /P350 3
0.80
0.73
0.91
0.61
0.78
0.80
0.55
1.31
0.65
1.42
0.59
0.74
0.72
0.82
1.29
0.71
1.70
0.70
0.94
0.79
1.05
0.90
A.4
Polarziation Spectrum: 450 um vs 350 um at
RA < 18h17m30s
∆α1
∆δ 1 P450
2.5
-73.6 2.0
2.5
57.0
1.2
-0.0
-0.0
1.4
-2.5 -57.0 1.6
-5.0
16.6
1.3
-7.4 -38.0 2.0
-9.9
33.2
1.1
-12.4 -21.4 2.1
-14.9 49.9
0.8
-17.3 -4.8
1.5
-24.8 -45.1 0.8
-29.7 -26.1 1.8
-34.6 -9.5
1.9
-42.1 80.7
0.7
-44.5 -104.5 3.4
-47.0 -30.9 1.5
-49.5 -87.9 3.8
-56.9
2.4
1.2
-59.4 76.0
1.5
-61.9 -109.3 4.8
-66.8 -92.6 4.5
-66.8 -19.0 1.6
-71.7 54.6
0.7
-76.7 71.2
1.4
-89.1 -80.8 6.3
-94.0 66.5
1.7
-94.0 -64.1 4.4
-94.0
9.5
1.3
σp P.A.2
0.2
0.4
0.1 11.3
0.1 -15.1
0.2 -8.5
0.1 -22.2
0.1 -7.4
0.1 -18.6
0.1 -13.5
0.1 -6.5
0.1 -19.8
0.1 -20.1
0.1 -13.2
0.1 -12.9
0.1 -8.5
0.3 -46.1
0.1 -27.3
0.4 -43.5
0.1 -16.6
0.2 -26.3
0.4 -47.7
0.3 -45.5
0.1 -29.3
0.1 -55.4
0.2 -49.6
0.9 -49.8
0.4 -52.9
1.1 -50.4
0.3 -39.6
σP.A.
2.9
2.8
1.4
2.7
1.8
1.4
2.3
1.0
2.7
1.3
4.5
1.8
1.2
4.0
2.6
2.7
2.4
1.3
3.4
2.2
1.9
2.5
5.0
4.9
3.3
6.9
6.5
8.1
P350
0.6
0.5
1.6
1.1
1.1
1.2
0.7
1.7
0.4
1.4
0.8
1.1
1.4
0.6
2.1
1.4
2.5
0.9
0.5
2.8
3.7
1.5
0.2
0.9
3.3
0.8
3.6
1.9
σp
0.1
0.1
0.0
0.1
0.0
0.1
0.0
0.0
0.0
0.0
0.1
0.1
0.1
0.0
0.2
0.1
0.1
0.1
0.1
0.3
0.2
0.1
0.1
0.1
0.3
0.2
0.3
0.5
P.A.2
2.3
6.6
167.3
173.4
162.1
174.5
156.9
171.4
174.3
167.1
153.8
159.0
165.7
179.1
141.6
143.0
140.7
164.5
151.3
136.5
136.9
147.7
123.4
128.6
135.8
128.3
139.3
134.1
Offsets in arcseconds from 18h 17m 31.4s ,-16◦ 14′ 25′′ (B1950.0).
Position angle of E vector east from north.
3
Median = 1.485, mean = 1.624 and std = 0.688.
1
2
130
σP.A.
3.3
2.9
0.6
1.7
0.8
1.2
1.6
0.6
3.7
0.7
2.1
1.8
1.3
2.0
2.3
2.0
1.4
2.5
3.1
3.4
1.3
1.9
10.8
1.8
2.9
7.6
2.3
7.1
P450 /P350 3
3.33
2.40
0.87
1.45
1.18
1.67
1.57
1.24
2.00
1.07
1.00
1.64
1.36
1.17
1.62
1.07
1.52
1.33
3.00
1.71
1.22
1.07
3.50
1.56
1.91
2.12
1.22
0.68
Figure A.3: 350 um polarization vectors from Hertz ([24]) and the 450 um result from
SHARP (smoothed to 20′′ resolution, Red), center at 18h 17m 32s ,-16◦ 14′ 25′′ (B1950.0).
Blue: Hertz vectors at RA > 18h 17m 30s , Green: Hertz vectors at RA < 18h 17m 30s
131
A.5
Polarization Vectors
∆α1
∆δ 1
P
σp
P.A.2
σP.A.
∆α
∆δ
P
σp
P.A.
σP.A.
70.2
-114.0
5.8
2.5
51.7
12.1
-18.9
-19.0
2.5
0.2
-18.4
2.7
70.2
-95.0
5.0
2.1
36.4
11.9
-18.9
-9.5
1.6
0.2
-23.6
3.9
70.1
-57.0
3.1
1.5
32.0
12.8
-18.9
-0.0
1.4
0.3
-34.6
5.9
70.1
-38.0
3.4
1.7
5.6
13.7
-18.9
9.5
1.4
0.3
-29.1
5.5
70.1
76.0
10.1 5.0
37.3
13.3
-18.9
19.0
1.6
0.2
-26.9
3.8
60.3
-47.5
2.6
0.8
36.1
8.8
-18.9
28.5
1.3
0.3
-19.8
7.6
60.2
-19.0
2.5
0.8
14.7
8.4
-18.9
38.0
1.2
0.3
-20.4
7.8
60.2
-9.5
2.2
0.9
28.8
11.7
-18.9
47.5
1.0
0.3
-19.2
8.9
60.2
-0.0
2.6
1.1
21.8
11.4
-18.9
57.0
1.0
0.3
-2.1
9.4
60.2
9.5
2.8
0.9
3.4
8.3
-18.9
66.5
1.9
0.4
-3.9
5.4
60.2
19.0
4.1
2.0
25.7
12.4
-18.9
76.0
1.1
0.2
2.8
6.3
60.2
28.5
5.0
1.3
27.5
6.7
-18.9
85.5
1.6
0.2
2.0
3.2
60.2
38.0
3.6
1.6
17.3
12.6
-18.9
95.0
1.2
0.3
10.3
7.2
50.4
-95.0
1.9
0.7
43.9
10.8
-18.9
104.5
1.7
0.8
30.2
12.8
50.4
-85.5
2.7
0.7
48.8
7.2
-28.8
-47.5
1.0
0.5
-34.8
13.3
50.4
-76.0
3.8
1.1
33.0
8.3
-28.8
-28.5
2.0
0.3
-8.6
4.9
50.4
-19.0
1.9
0.9
31.0
13.9
-28.8
-19.0
2.9
0.8
-3.0
8.0
50.4
-0.0
2.1
0.8
6.1
10.3
-28.8
-9.5
1.3
0.3
-22.3
6.0
50.4
9.5
1.6
0.7
-8.6
12.0
-28.8
-0.0
1.2
0.2
-26.0
5.8
50.4
28.5
3.1
0.8
17.5
7.4
-28.8
9.5
1.4
0.3
-31.2
6.1
50.3
47.5
2.8
1.0
33.1
9.5
-28.8
19.0
1.0
0.3
-33.3
7.7
40.5
-85.5
2.4
1.0
23.1
11.4
-28.8
28.5
0.8
0.3
-39.5
9.4
40.5
-66.5
3.7
1.3
42.9
9.3
-28.8
38.0
1.0
0.4
-12.5
13.2
40.5
-57.0
1.9
0.8
32.9
11.8
-28.8
47.5
0.7
0.2
-7.9
9.3
40.5
-47.5
2.0
0.7
49.5
9.5
-28.8
57.0
1.0
0.2
15.6
5.7
40.5
-28.5
2.1
0.6
36.4
7.9
-28.8
66.5
1.0
0.2
0.8
4.9
40.5
-0.0
1.7
0.7
6.8
10.9
-28.8
76.0
1.1
0.2
-15.0
4.8
40.5
9.5
2.4
0.6
0.8
7.1
-28.8
85.5
1.4
0.2
5.7
5.1
132
40.5
19.0
2.5
0.8
20.9
8.8
-28.8
95.0
1.0
0.2
12.3
6.6
40.5
38.0
3.7
1.1
16.5
6.9
-28.8
104.5
1.1
0.5
40.3
12.7
30.6
-104.5
1.8
0.9
42.6
14.3
-38.7 -104.5
1.8
0.9
-38.8
13.8
30.6
-95.0
2.2
0.7
33.5
8.1
-38.7
-76.0
8.8
3.3
-71.6
10.1
30.6
-85.5
1.6
0.7
40.6
13.0
-38.7
-28.5
1.7
0.5
-3.3
8.7
30.6
-76.0
3.7
1.0
46.3
6.8
-38.7
-19.0
3.1
0.4
-7.6
3.6
30.6
-66.5
2.1
1.0
45.4
13.9
-38.7
-9.5
2.6
0.4
-6.3
3.8
30.6
-57.0
1.6
0.7
7.0
11.8
-38.7
-0.0
1.4
0.2
-10.7
4.0
30.6
-38.0
2.0
0.6
11.0
8.9
-38.7
9.5
1.1
0.2
-32.1
4.7
30.6
-28.5
2.1
0.8
12.9
11.2
-38.7
19.0
1.3
0.3
-37.8
7.6
30.6
-0.0
1.2
0.6
17.2
13.8
-38.7
28.5
1.0
0.2
-41.7
6.9
30.6
9.5
2.1
0.6
-7.7
7.7
-38.7
38.0
1.1
0.3
-43.9
6.6
30.6
28.5
2.0
0.9
15.7
13.2
-38.7
76.0
1.3
0.4
18.4
8.8
20.7
-104.5
1.9
0.7
51.7
10.5
-38.7
95.0
1.2
0.2
11.8
5.8
20.7
-95.0
1.8
0.7
47.9
11.8
-48.6 -104.5
3.1
1.4
89.6
12.8
20.7
-85.5
2.8
0.5
36.6
5.4
-48.6
-95.0
5.2
1.2
-37.6
6.2
20.7
-76.0
3.5
0.7
36.0
5.7
-48.6
-76.0
4.4
2.0
-75.1
12.3
20.7
-66.5
2.1
0.7
41.0
9.0
-48.6
-57.0
3.9
1.3
-72.4
9.5
20.7
-57.0
0.8
0.4
30.5
14.0
-48.6
-38.0
1.1
0.5
-42.3
12.9
20.7
-47.5
2.1
0.5
23.5
6.7
-48.6
-28.5
1.3
0.6
-19.8
13.6
20.7
-38.0
1.5
0.5
11.1
9.5
-48.6
-19.0
2.9
0.7
-6.2
6.3
20.7
-28.5
2.4
0.5
-0.4
6.1
-48.6
-9.5
1.5
0.4
-10.4
7.2
20.7
-9.5
1.5
0.5
6.9
9.4
-48.6
-0.0
1.7
0.2
-17.2
3.2
20.7
-0.0
2.3
0.5
4.1
5.6
-48.6
9.5
1.3
0.1
-28.0
2.5
20.7
28.5
2.1
1.0
28.3
13.1
-48.6
19.0
0.9
0.2
-21.5
5.6
20.7
47.5
1.6
0.7
23.5
13.0
-48.6
28.5
0.5
0.1
-32.0
7.1
20.7
66.5
2.4
0.9
26.6
10.5
-48.6
38.0
0.8
0.1
-43.7
5.2
20.7
76.0
2.8
1.2
42.8
11.6
-48.6
47.5
0.5
0.2
-35.5
10.4
20.7
85.5
3.0
1.3
25.2
11.9
-48.6
66.5
1.0
0.2
3.6
6.2
10.8
-85.5
3.2
1.3
0.1
10.1
-48.6
76.0
0.7
0.2
-31.6
10.3
133
10.8
-66.5
2.9
0.7
24.8
6.7
-48.6
95.0
1.2
0.4
30.1
10.2
10.8
-57.0
1.7
0.4
15.1
6.6
-48.6
104.5
1.3
0.6
29.0
13.6
10.8
-47.5
1.2
0.3
0.6
6.8
-58.5 -114.0
6.2
3.0
-64.0
12.5
10.8
-38.0
1.5
0.3
-1.1
6.1
-58.5 -104.5
3.0
0.9
-56.9
8.5
10.8
-28.5
2.0
0.5
-7.8
6.8
-58.5
-95.0
3.3
0.8
-36.6
6.9
10.8
-19.0
2.2
0.6
2.1
8.2
-58.5
-85.5
6.4
2.3
-36.3
8.8
10.8
-9.5
2.5
0.6
0.2
6.7
-58.5
-57.0
3.2
1.4
-70.9
11.9
10.8
-0.0
1.6
0.5
3.6
7.9
-58.5
-28.5
2.2
0.6
-42.3
7.0
10.8
9.5
1.0
0.4
22.6
11.9
-58.5
-19.0
2.7
0.6
-16.1
6.3
10.8
19.0
1.0
0.5
15.3
13.3
-58.5
-9.5
2.9
0.5
-7.1
4.8
10.8
28.5
1.8
0.6
20.7
8.7
-58.5
-0.0
1.4
0.3
-7.7
5.5
10.8
38.0
2.6
0.6
19.6
6.6
-58.5
9.5
1.1
0.2
-3.9
4.0
10.8
47.5
1.6
0.6
26.5
10.0
-58.5
28.5
0.5
0.2
-30.0
10.5
10.8
66.5
2.3
0.9
9.6
11.9
-58.5
38.0
0.9
0.2
-40.6
6.4
10.8
76.0
2.8
1.4
19.5
14.1
-58.5
57.0
1.3
0.3
-30.2
8.0
10.8
114.0
5.0
2.0
24.1
11.3
-58.5
66.5
3.0
0.4
-4.3
3.9
0.9
-104.5
1.7
0.7
33.2
11.5
-58.5
76.0
1.2
0.4
-7.7
9.9
0.9
-85.5
1.8
0.7
24.1
11.1
-68.4 -114.0 11.1 4.2
-52.5
7.8
0.9
-76.0
2.1
0.8
5.0
10.8
-68.4 -104.5
6.2
1.1
-46.9
4.3
0.9
-66.5
2.2
0.5
-3.7
7.1
-68.4
-95.0
3.4
0.7
-41.1
5.4
0.9
-57.0
2.4
0.4
-7.6
5.2
-68.4
-85.5
3.9
0.9
-54.6
6.0
0.9
-47.5
2.2
0.3
-9.5
4.1
-68.4
-38.0
2.2
1.0
-64.1
12.2
0.9
-38.0
2.8
0.3
-4.7
2.9
-68.4
-28.5
2.5
0.5
-42.1
5.9
0.9
-28.5
2.6
0.3
-3.2
3.6
-68.4
-19.0
2.1
0.5
-28.6
6.2
0.9
-19.0
1.4
0.4
-3.1
8.0
-68.4
-9.5
2.0
0.4
-23.2
5.9
0.9
-9.5
1.6
0.3
-4.2
6.2
-68.4
-0.0
1.6
0.3
-18.6
4.6
0.9
-0.0
1.8
0.4
-17.7
6.5
-68.4
9.5
0.7
0.1
-20.5
5.0
0.9
9.5
1.1
0.4
-2.1
11.1
-68.4
19.0
0.9
0.1
-18.3
4.3
0.9
19.0
1.6
0.8
-4.1
13.1
-68.4
28.5
0.5
0.1
-2.1
6.9
0.9
38.0
1.4
0.4
17.0
9.3
-68.4
47.5
1.0
0.3
-75.8
7.5
134
0.9
47.5
1.8
0.4
5.4
6.9
-68.4
57.0
1.2
0.4
-65.4
10.4
0.9
57.0
1.3
0.4
16.6
9.0
-68.4
66.5
2.1
0.7
-31.4
9.0
0.9
66.5
1.5
0.6
18.3
10.8
-68.4
76.0
2.2
0.8
-1.6
10.3
0.9
123.5
16.6 8.0
25.1
12.0
-78.3
-95.0
7.4
1.5
-41.7
4.6
-9.0
-66.5
1.7
0.6
-8.6
11.2
-78.3
-85.5
4.2
1.1
-42.0
6.6
-9.0
-57.0
2.1
0.6
-14.0
8.7
-78.3
-76.0
5.2
1.3
-54.0
6.3
-9.0
-47.5
2.1
0.7
-3.4
9.8
-78.3
-38.0
5.1
1.3
-69.2
7.0
-9.0
-38.0
2.5
0.4
-8.5
4.5
-78.3
-28.5
3.3
1.3
-67.2
11.3
-9.0
-28.5
2.4
0.3
-8.3
3.1
-78.3
-19.0
1.2
0.6
-43.4
14.3
-9.0
-19.0
2.2
0.2
-18.9
2.9
-78.3
-9.5
1.6
0.5
-48.6
9.0
-9.0
-9.5
2.0
0.3
-8.8
4.4
-78.3
9.5
1.9
0.4
-18.0
5.4
-9.0
-0.0
1.4
0.3
-10.1
5.7
-78.3
28.5
1.0
0.2
-9.2
5.9
-9.0
9.5
1.7
0.3
-20.7
5.5
-78.3
66.5
3.0
0.8
-29.3
7.8
-9.0
19.0
1.3
0.3
-15.0
7.6
-88.2
-85.5
5.1
2.2
-55.5
8.9
-9.0
38.0
1.9
0.6
-6.4
8.9
-88.2
-76.0
6.5
2.4
-50.2
7.0
-9.0
57.0
1.2
0.5
14.2
11.8
-88.2
-66.5
5.9
2.3
-40.5
9.6
-9.0
66.5
1.3
0.5
13.4
9.8
-88.2
-28.5
2.7
1.1
-37.4
10.9
-9.0
76.0
1.2
0.3
-32.0
8.1
-88.2
-19.0
2.3
1.1
-16.1
13.1
-9.0
85.5
1.1
0.3
-18.6
6.6
-88.2
-9.5
3.5
0.8
-24.2
6.7
-9.0
95.0
1.7
0.5
17.6
9.2
-98.1
-57.0
4.3
1.5
-50.4
9.2
-18.9
-47.5
1.5
0.5
11.1
9.6
-98.1
-9.5
4.3
1.4
-15.2
9.1
-18.9
-38.0
1.9
0.4
1.9
5.6
-98.1
-0.0
2.6
0.7
-45.7
8.1
-18.9
-28.5
1.4
0.3
-8.3
5.8
-98.1
47.5
1.2
0.4
-47.4
9.3
Offsets in arcseconds from 18h 17m 32s ,-16◦ 14′ 25′′ (B1950.0).
2
Position angle of E vector east from north.
1
135
Appendix B
Blackbody Radiation
All matter emits electromagnetic radiation when it has a temperature above absolute zero. A black body is an idealized physical body that absorbs all incident
radiation. Because of this perfect absorptivity at all wavelengths, a black body is
also the best emitter of thermal radiation, which it radiates incandescently in a characteristic, continuous spectrum that depends on the body’s temperature.
The thermal radiation from a black body is called black body radiation. Planck’s
law describes the radiation from a black body with a temperature of T:
Bν (T ) =
1
2hν 3
c2 ehν/(kT ) − 1
(B.1)
Where h is Planck’s constant, c is the speed of light, k is Boltzmann’s constant
and Bν (T ) is in the unit of Js−1 m−2 sr −1 Hz −1 .
In the Wien limit, where hν ≫ kT , the Plank’s spectrum is approximately:
Bν (T ) ≈
2hν 3 −hν/(kT )
e
c2
(B.2)
At low frequency range, where hν ≪ kT (Rayleigh-Jeans limit), it is approxi-
mately:
Bν (T ) ≈ 2kT ν 2 /c2
(B.3)
Figure B.1 shows the Plank spectrum, Wien limit and Rayleigh-Jeans limit of a
black body with a temperature of 2.725K. The black body radiation spectrum peaks
136
[
−
%ODFN%RG\5DGLDWLRQ7 .
3ODQFN
:LHQ
5D\OHLJK−-HDQV
ν
−
% -V
P − VU− +]− ν*+]
Figure B.1: The Planck, Wien and Rayleigh-Jeans spectrum of a 2.725 K black body.
The Wien limit is a good approximation at ν > 250 GHz and the Rayleigh-Jeans
limit works well below 20 GHz.
at ∂Bν /∂ν = 0:
νpeak ≈ 2.82kT /h = 58.7 ×
T
GHz.
K
(B.4)
The CMB has a thermal black body spectrum at a temperature of Tcmb = 2.725
K. In the Planck spectrum, it peaks at the microwave range frequency of about 160.2
GHz, corresponding to a wavelength of 1.873 mm.
137
Appendix C
NEP of Photons in a Blackbody
Radiation Field
1
The variance in the number n of photons in a given state x = hν/(kB Ts ), is
σ 2 = n(n + 1), where
n(ν) = n(x) =
αǫf
−1
ex
(C.1)
where f is the transmissivity of the optics, Ts , ǫ are the temperature and emissivity
of the source, α is the detector absorptivity.
Then, the variance in energy is n(n+1)h2 ν 2 . The number of states traveling toward
the detector in a volume of ctA, is (2ν 2 /c3 )ctAΩdν, where 2ν 2 /c3 is the number of
states per unit volume per solid angle per frequency [25], Ω is the solid angle of the
beam, A is the effective area, and t is the integration time. The total number of states
in the waveband is:
Z
(2ν 2 /c3 )ctAΩdν
Then the total variance of energy is:
Z
2
σ = (2ν 2 /c3 )ctAΩn(n + 1)h2 ν 2 dν
Z
2AΩ (kB Ts )5
x4
αǫf
=t 2
(1
+
)(αǫf )dx
c
h3
ex − 1
ex − 1
1
This chapter is mostly from [142]
138
(C.2)
(C.3)
NEP is defined as the error in power in a half-second integration (section 4.2.1):
2σ 2
t
Z
x4
4AΩ (kB Ts )5
αǫf
= 2
(1 + x
)(αǫf )dx
3
x
c
h
e −1
e −1
NEP2 =
NEP has the unit of W2 Hz−1/2 .
139
(C.4)
Appendix D
A Low Cross-Polarization
Smooth-Walled Horn with
Improved Bandwidth
1
Many precision microwave applications, including those associated with radio
astronomy, require feedhorns with symmetric E- and H-plane beam patterns that
possess low sidelobes and cross-polarization control. A common approach to achieving these goals is a “scalar” feed, which has a beam response that is independent of
azimuthal angle. Corrugated feeds [165] approximate this idealization by providing
the appropriate boundary conditions for the HE11 hybrid mode at the feed aperture.
Alternatively, an approximation to a scalar feed can be obtained with a multimode
feed design. One such “dual-mode” horn is the Potter horn [166]. In this implementation, an appropriate admixture of T M11 is generated from the initial T E11 mode
using a concentric step discontinuity in the waveguide. The two modes are then
phased to achieve the proper field distribution at the feed aperture using a length of
waveguide. The length of the phasing section limits the bandwidth due to the dispersion between the modes. Lier [167] has reviewed the cross-polarization properties
of dual-mode horn antennas for selected geometries. Other authors have produced
variations on this basic design concept [168, 169]. Improvements in the bandwidth
1
This appendex is from [156]
140
have been realized by decreasing the phase difference between the two modes by 2π
[170, 171].
To increase the bandwidth, it is possible to add multiple concentric step continuities with the appropriate modal phasing [172, 173]. A variation on this technique is
to use several distinct linear tapers to generate the proper modal content and phasing
[174, 175]. Operational bandwidths of 15-20% have been reported using such techniques. A related class of devices is realized by allowing the feedhorn profile to vary
smoothly rather than in discrete steps. Examples of such smooth-walled feedhorns
with ∼15% fractional bandwidths exist in the literature [162, 176].
In this work, we describe the design and optimization of a smooth-walled feed that
has a 30% operational bandwidth, over which the cross-polarization response is better
than -30 dB. The optimization technique is described, and the performance of the feed
is compared with other published dual-mode feedhorns. The feedhorn described here
has a monotonic profile that allows it to be manufactured by progressively milling
the profile using a set of custom tools.
D.1
Smooth-walled Feedhorn Optimization
The performance of a feedhorn can be characterized by angle- and frequencydependent quantities that include beam width, sidelobe response and cross-polarization.
Quantities such as reflection coefficient and polarization isolation that only depend
on frequency are also important considerations. All of these functions are dependent
upon the shape of the feed profile. In the optimization approach described, a weighted
penalty function is used to explore and optimize the relationship between the feed
profile and the electromagnetic response.
D.1.1
Beam Response Calculation
The smooth-walled horn was approximated by a profile that consists of discrete
waveguide sections, each of constant radius. With this approach, it was important
to verify that each section is thin enough that the model is a valid approximation of
141
the continuous profile. For profiles relevant to our design parameters, section lengths
of ∆l ≤ λc /20 were found to be sufficient by trial and error, where λc is the cutoff
wavelength of the input waveguide section. It is possible in principle to dynamically
set the length of each section to optimize the approximation to the local curvature of
the horn. This would increase the speed of the optimization; however, for simplicity,
this detail was not implemented in our study.
For each trial feedhorn the angular response was calculated directly from the modal
content at the feed aperture. This in turn was calculated as follows. The throat
of the feedhorn was assumed to be excited by the circular waveguide T E11 mode.
The modal content of each successive section was then determined by matching the
boundary conditions at each interface using the method of James [18]. The cylindrical
symmetry of the feed limits the possible propagating modes to those with the same
azimuthal functional form as T E11 [177]. This azimuthal-dependence extends to
the resulting beam patterns, allowing the full beam pattern to be calculated from
the E- and H- plane angular response. Ludwig’s third definition [178] is employed
in calculation and measurement of cross-polar response. We note that an additional
consequence of the feedhorn symmetry is that to the extent that the E- and H-planes
are equal in both phase and amplitude, the cross-polarization is zero [159]. Changes
in curvature in the feed profile can excite higher order modes (e.g., T E12 and T M12 ),
the presence of which can potentially degrade the cross-polarization response of the
horn.
D.1.2
Penalty Function
We constructed a penalty function to optimize the antenna profile. The penalty
function with normalized weights, αj , is written as
χ2 =
N X
M
X
i=1 j=1
αj ∆j (fi )2 ,
(D.1)
where i sums over a discrete set of (N) frequencies in the optimization frequency
band, and j sums over the number (M) of discrete parameters one wishes to take
into account for the optimization. In the parameter space considered, this function
142
was minimized over the frequency range 1.25fc < f < 1.71fc (∆f /f0 =0.3) to find
the desired solution. Results reported here were obtained by restricting this penalty
function to include only the cross-polarization and reflection (|S11 |2 ) with uniform
weights (M = 2). Additional parameters were explored; however, they were found to
be subdominant in producing the target result. These functions were evaluated at 13
equally-spaced frequency points in Equation D.1. The explicit forms used for ∆1 (f )
and ∆2 (f ) are
∆1 (f ) =
(
XP (f ) − XP0 if XP (f ) > XP0 ,
(D.2)
∆2 (f ) =
(
RP (f ) − RP0 if RP (f ) > RP0 ,
(D.3)
0
if XP (f ) ≤ XP0 ,
0
if RP (f ) ≤ RP0 ,
where XP (f ) and RP (f ) are the maximum of the cross-polarization XP (f ) =
Max[XP (f, θ)] and reflected power at frequency f , respectively. XP0 and RP0 are
the threshold cross-polarization and reflection. If either the cross-polarization or reflection at a sampling frequency were less than its critical value, it was omitted from
the penalty function. Otherwise, its squared difference was included in the sum in
Equation D.1.
D.1.3
Feedhorn Optimization
The feedhorn was optimized in a two-stage process that employed a variant of
Powell’s method [160]. Generically, this algorithm can produce an arbitrary profile.
To produce a feed that is easily machinable, we restricted the optimization to the
subset of profiles for which the radius increases monotonically along the length of the
horn. Without this constraint, this method was observed to explore solutions with
corrugated features and the serpentine profiles explored in [161].
The aperture diameter of the feedhorn was initially set to ∼ 4λc , but was allowed
to vary slightly to achieve the desired beam size. A single discontinuity exists between the circular waveguide and the feed throat. The remainder of the horn profile
adiabatically transitions to the feed aperture. The total length of the feedhorn from
143
the aperture to the single mode waveguide was fixed at 12.3 λc during optimization.
This length is somewhat arbitrary, but chosen to produce a stationary phase center
and a diffraction-limited beam in a practical volume.
The approach of [162] was followed as an initial input to the Powell method.
Specifically, the feed radius, r, is written analytically as a function of the distance
along the length of the horn, z, as:
r(z) =
(
0.293 + 0.703 sin0.75 (0.255z)
0.293 + 0.703{1 + [0.282(z − 6.15)]2 }
1
2
0 ≤ z ≤ 6.15,
6.15 < z ≤ 12.30,
(D.4)
where parameters are given in units of λc . This profile was then approximated by
natural spline of a set of 20 points equally-spaced along the feed length. Throughout
the optimization, we explicitly imposed the condition that radius of each section be
greater than or equal to that of the previous section. This sampling choice effectively
limits the allowed change in curvature along the feed profile. In the first stage of
optimization, both XP0 and RP0 were set to -30 dB. The minimum of the penalty
function was found by the modified Powell method in this 20-dimension space.
In the second stage of the optimization, the number of points explicitly varied
along the profile was increased to 560. The modified Powell method was used to
optimize the profile in this 560-dimensional space. In this stage, both of XP0 and
RP0 were decreased to -34 dB.
In principle, it is possible to use either of these techniques alone to find our
solution. There are enough degrees of freedom in the 20-point spline to do so and the
560-point technique should be able to recover the solution regardless of the starting
point. We found, however, that the 20-point spline did not converge readily to the
final profile given the initial conditions above, but rather converged to a broad local
minimum. In addition to finding the general features of the desired performance, this
first stage of optimization provided a significant reduction in the use of computing
resources compared to the slower 560-point parameter search.
Figure D.1 shows the initial, intermediate, and final feedhorn profiles. It is possible
to approximate the final profile with a 20-point spline. The final profile of the feed
144
3
2
Radius/λc
1
0
−1
−2
−3
−2
Initial Profile
Intermediate Profile
Final Profile
0
2
4
Length/λc
6
8
10
12
Figure D.1: The initial, intermediate and final profiles are shown. All dimensions are
given in units of the cuttoff wavelength of the input circular waveguide.
is reproduced with a low-spatial frequency error of ∼ 0.015λc . This effect has a
negligible influence on the modeled performance. This suggests that the optimization
procedure could be done completely using a spline with fewer than 20 points if the
location of the spline points were dynamically varied. Future optimization algorithms
could be made more efficient by implementing this approach.
Figure D.2 shows the improvement in cross-polarization for the two stages of
optimization. The reflection is also shown for the initial profile, the intermediate
optimization, and the final feedhorn profile.
D.2
Feedhorn Fabrication and Measurement
A feed (Figure D.3) that operates in circular waveguide with a T E11 cutoff frequency of fc =26.36 GHz was fabricated to test the proposed design. The structure
was optimized between 33 and 45 GHz. The prototype feed was manufactured via
electroforming in order to validate the design using a process that allows the feed
structure to be measured and compared to the design profile. The final design profile
is well-approximated by splining the radius (r) as a function of length (z) provided
in Table D.1. The full 560-point profile is available upon request.
145
Maximum Cross-Pol (dB)
−18
−22
−26
−30
−34
Initial Guess
Intermediate Solution
Final Profile
Measurements
Return Loss (dB)
−15
−25
−35
−45
−55
1
1.2
1.4
1.6
1.8
2
f/fc
Figure D.2: (Top) The maximum cross-polar response across the band is shown for
the three profiles in Figure D.1. Measurements of the maximum cross-polarization
are superposed. (Bottom) The reflected power measurements for the final feed horn
are shown plotted over the predicted reflected power for the initial, intermediate, and
final feedhorn profiles. Frequency is given in units of the cutoff frequency of the input
circular waveguide.
146
The feedhorn was measured in the Goddard Electromagnetic Anechoic Chamber
(GEMAC). The receivers and microwave sources used in the measurement provide
a > 50 dB dynamic range from the peak response over ∼ 2π steradians with an
absolute accuracy of < 0.5 dB. A five section constant cutoff transition from rectangular waveguide (WR 22.4, fc = 26.36 GHz) to circular waveguide [179] was used
to mate the feedhorn to the rectangular waveguide of the antenna range infrastructure. The constant cutoff condition was maintained in the transition by ensuring
acircle = abroadwall s11 /π where acircle is the radius of the circular guide, abroadwall is the
width of the broadwall of the rectangular guide, and s11 ∼ 1.841 is the eigenvalue
for the T E11 mode [158]. The alignment of the circular waveguide feed interface was
maintained to avoid degradation of the cross-polar antenna response. Pinning of this
interface as specified in [180] or similar is recommended.
Beam plots and parameters at the extrema and the middle of the optimization
frequency range are shown in Figure D.4 and Table D.2. The cross-polarization
response as a function of frequency of this device is compared to other published
implementations of multi-mode scalar feeds (Fig. D.5). As is common for applications
requiring the beam symmetry provided by a scalar horn, the aperture efficiency is low.
In addition, we note that the phase center for this horn is near the aperture and is
stable in frequency.
An HP8510C network analzyer was used to measure the reflected power (see Fig.
D.2) with a through-reflect-line calibration in circular waveguide. If desired, the
match at the lower band edge can be improved by using a transition to a larger
diameter guide. The measured observations are in agreement with theory.
Imperfections in the profile may occur during manufacturing due to chattering of
the tooling or similar physical processes. We performed a tolerance study to determine the effect of such high-spatial frequency errors in the feed radius. Negligible
degradation in performance was observed for Gaussian errors in the radius up to
0.002 λc . The feed’s monotonic profile is compatible with machining by progressive
plunge milling in which successively more accurate tools are used to realize the feed
profile. This technique has been used for individual feeds and is potentially useful
for fabricating large arrays of feedhorns. Examples include fabrication of multimode
147
Table D.1: Spline Approximation to Optimized Profile (in Millimeters)
Section Length (z) Radius (r)
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
0.0
7.0
14.0
21.0
28.0
35.0
42.0
49.0
56.0
63.0
70.0
77.0
84.0
91.0
98.0
105.0
112.0
119.0
126.0
133.0
140.0
3.33
5.77
7.91
9.90
10.86
11.13
11.27
11.66
11.90
11.96
12.24
12.44
12.76
13.70
15.40
17.01
17.71
20.05
21.75
21.91
21.92
Winston concentrators [181, 182], direct-machined smooth-walled conical feed horns
for the South Pole Telescope [183], and the exploration of this technique for dual-mode
feedhorns [174].
D.3
Conclusion
An optimization technique for a smooth-walled scalar feedhorn has been presented.
Using this flexible approach, we have demonstrated a design having a 30% bandwidth
with cross-polar response below -30 dB. The design was tested in the range 33-45
GHz and found to be in agreement with theory. The design’s monotonic profile and
tolerance insensitivity enable the manufacturing of such feeds by direct machining.
148
Figure D.3: A smooth-walled feedhorn operating between 33 and 45 GHz was constructed. The horn is 140 mm long with an aperture radius of 22 mm. The input
circular waveguide radius is 3.334 mm.
149
Frequency
[GHz]
33
34
35
36
37
38
39
40
41
42
43
44
45
Table D.2: Beam Parameters
Wavelength Antenna Gain Beam Solid Angle
[mm]
[dBi]
[Sr]
9.09
21.3
0.0925
8.82
21.1
0.0984
8.57
21.4
0.0904
8.33
21.3
0.0929
8.11
21.3
0.0930
7.89
21.9
0.0815
7.69
22.0
0.0788
7.50
22.7
0.0676
7.32
22.9
0.0643
7.14
23.5
0.0556
6.98
23.7
0.0540
6.82
24.2
0.0479
6.67
24.2
0.0473
This approach is useful in applications where a large number of feeds are desired in
a planar array format.
150
-10
-20
E-plane
Power (dB)
45 GHz
39 GHz
33 GHz
0
-30
-40
-50
-10
H-plane
Power (dB)
0
-20
-30
-40
-50
-10
D-plane
Power (dB)
0
-20
-30
-40
-50
-60
-80
-60
-40
-20
0
20
40
60
Azimuth Angle(degrees)
Measured Co-Pol
80
-80
-60
-40
-20
0
20
40
60
Azimuth Angle(degrees)
80
-80
Measured Cross-Pol
Predicted Co-Pol
-60
-40
-20
0
20
40
60
Azimuth Angle(degrees)
80
Predicted Cross-Pol
Figure D.4: The measured E-, H-, and diagonal-plane angular responses for the lower
edge (33 GHz), center (39 GHz), and upper edge (45 GHz) of the optimization band
are shown. The cross-polar patterns in the diagonal plane are shown in the bottom
three panels for each of the three frequencies.
151
Cross−Polarization(dB)
−25
−30
−35
−40
This Work
Yassin 2007
Granet 2004
Neilson 2002
Pickett 1984
Potter 1963
0.85
0.9
0.95
1
1.05
Normalized Frequency
1.1
1.15
Figure D.5: The maximum cross-polar response of the prototype feedhorn is compared
to other implementations of smooth-walled feedhorns. The data presented have been
normalized to the design center frequencies as specified by the respective authors.
152
Appendix E
CLASS 40 GHz Feedhorn Profile
Step
Length
Radius Step
Length
Length
Radius
-
mm
mm
-
mm
mm
-
mm
mm
0
0.000
3.334
167
33.400
9.529
334
66.800
11.710
1
0.200
3.383
168
33.600
9.537
335
67.000
11.785
2
0.400
3.432
169
33.800
9.544
336
67.200
11.860
3
0.600
3.481
170
34.000
9.551
337
67.400
11.935
4
0.800
3.531
171
34.200
9.557
338
67.600
12.012
5
1.000
3.580
172
34.400
9.563
339
67.800
12.089
6
1.200
3.629
173
34.600
9.569
340
68.000
12.167
7
1.400
3.678
174
34.800
9.575
341
68.200
12.246
8
1.600
3.727
175
35.000
9.580
342
68.400
12.325
9
1.800
3.776
176
35.200
9.585
343
68.600
12.404
10
2.000
3.825
177
35.400
9.590
344
68.800
12.485
11
2.200
3.874
178
35.600
9.595
345
69.000
12.566
12
2.400
3.923
179
35.800
9.599
346
69.200
12.647
13
2.600
3.972
180
36.000
9.604
347
69.400
12.729
14
2.800
4.021
181
36.200
9.608
348
69.600
12.811
15
3.000
4.070
182
36.400
9.612
349
69.800
12.894
16
3.200
4.119
183
36.600
9.616
350
70.000
12.977
153
Radius Step
17
3.400
4.168
184
36.800
9.619
351
70.200
13.061
18
3.600
4.217
185
37.000
9.623
352
70.400
13.145
19
3.800
4.265
186
37.200
9.626
353
70.600
13.229
20
4.000
4.314
187
37.400
9.630
354
70.800
13.313
21
4.200
4.363
188
37.600
9.633
355
71.000
13.398
22
4.400
4.412
189
37.800
9.636
356
71.200
13.483
23
4.600
4.460
190
38.000
9.640
357
71.400
13.568
24
4.800
4.509
191
38.200
9.643
358
71.600
13.652
25
5.000
4.558
192
38.400
9.646
359
71.800
13.737
26
5.200
4.606
193
38.600
9.649
360
72.000
13.822
27
5.400
4.655
194
38.800
9.653
361
72.200
13.907
28
5.600
4.703
195
39.000
9.656
362
72.400
13.992
29
5.800
4.752
196
39.200
9.659
363
72.600
14.077
30
6.000
4.800
197
39.400
9.663
364
72.800
14.162
31
6.200
4.848
198
39.600
9.666
365
73.000
14.246
32
6.400
4.897
199
39.800
9.670
366
73.200
14.330
33
6.600
4.945
200
40.000
9.674
367
73.400
14.414
34
6.800
4.993
201
40.200
9.678
368
73.600
14.498
35
7.000
5.041
202
40.400
9.682
369
73.800
14.581
36
7.200
5.089
203
40.600
9.686
370
74.000
14.664
37
7.400
5.137
204
40.800
9.690
371
74.200
14.746
38
7.600
5.185
205
41.000
9.694
372
74.400
14.828
39
7.800
5.233
206
41.200
9.698
373
74.600
14.909
40
8.000
5.280
207
41.400
9.703
374
74.800
14.990
41
8.200
5.328
208
41.600
9.707
375
75.000
15.070
42
8.400
5.376
209
41.800
9.712
376
75.200
15.150
43
8.600
5.423
210
42.000
9.716
377
75.400
15.229
44
8.800
5.471
211
42.200
9.721
378
75.600
15.307
45
9.000
5.518
212
42.400
9.725
379
75.800
15.384
46
9.200
5.565
213
42.600
9.729
380
76.000
15.461
154
47
9.400
5.612
214
42.800
9.734
381
76.200
15.536
48
9.600
5.660
215
43.000
9.738
382
76.400
15.611
49
9.800
5.707
216
43.200
9.743
383
76.600
15.685
50
10.000
5.754
217
43.400
9.747
384
76.800
15.758
51
10.200
5.800
218
43.600
9.751
385
77.000
15.830
52
10.400
5.847
219
43.800
9.755
386
77.200
15.901
53
10.600
5.894
220
44.000
9.759
387
77.400
15.970
54
10.800
5.940
221
44.200
9.763
388
77.600
16.039
55
11.000
5.987
222
44.400
9.767
389
77.800
16.107
56
11.200
6.033
223
44.600
9.770
390
78.000
16.173
57
11.400
6.079
224
44.800
9.774
391
78.200
16.238
58
11.600
6.126
225
45.000
9.777
392
78.400
16.302
59
11.800
6.172
226
45.200
9.780
393
78.600
16.364
60
12.000
6.218
227
45.400
9.783
394
78.800
16.425
61
12.200
6.263
228
45.600
9.786
395
79.000
16.485
62
12.400
6.309
229
45.800
9.788
396
79.200
16.543
63
12.600
6.354
230
46.000
9.791
397
79.400
16.599
64
12.800
6.400
231
46.200
9.793
398
79.600
16.654
65
13.000
6.445
232
46.400
9.794
399
79.800
16.708
66
13.200
6.490
233
46.600
9.796
400
80.000
16.760
67
13.400
6.535
234
46.800
9.797
401
80.200
16.810
68
13.600
6.580
235
47.000
9.798
402
80.400
16.859
69
13.800
6.625
236
47.200
9.799
403
80.600
16.906
70
14.000
6.669
237
47.400
9.799
404
80.800
16.951
71
14.200
6.713
238
47.600
9.799
405
81.000
16.995
72
14.400
6.758
239
47.800
9.800
406
81.200
17.037
73
14.600
6.802
240
48.000
9.801
407
81.400
17.078
74
14.800
6.845
241
48.200
9.802
408
81.600
17.118
75
15.000
6.889
242
48.400
9.803
409
81.800
17.156
76
15.200
6.933
243
48.600
9.804
410
82.000
17.192
155
77
15.400
6.976
244
48.800
9.805
411
82.200
17.228
78
15.600
7.019
245
49.000
9.806
412
82.400
17.262
79
15.800
7.062
246
49.200
9.807
413
82.600
17.294
80
16.000
7.105
247
49.400
9.808
414
82.800
17.325
81
16.200
7.147
248
49.600
9.809
415
83.000
17.355
82
16.400
7.189
249
49.800
9.810
416
83.200
17.384
83
16.600
7.232
250
50.000
9.811
417
83.400
17.412
84
16.800
7.274
251
50.200
9.812
418
83.600
17.438
85
17.000
7.315
252
50.400
9.813
419
83.800
17.464
86
17.200
7.357
253
50.600
9.814
420
84.000
17.488
87
17.400
7.398
254
50.800
9.815
421
84.200
17.511
88
17.600
7.439
255
51.000
9.816
422
84.400
17.533
89
17.800
7.480
256
51.200
9.817
423
84.600
17.554
90
18.000
7.521
257
51.400
9.818
424
84.800
17.574
91
18.200
7.561
258
51.600
9.819
425
85.000
17.593
92
18.400
7.601
259
51.800
9.820
426
85.200
17.612
93
18.600
7.641
260
52.000
9.821
427
85.400
17.629
94
18.800
7.681
261
52.200
9.822
428
85.600
17.645
95
19.000
7.720
262
52.400
9.823
429
85.800
17.661
96
19.200
7.759
263
52.600
9.824
430
86.000
17.676
97
19.400
7.798
264
52.800
9.825
431
86.200
17.689
98
19.600
7.837
265
53.000
9.826
432
86.400
17.703
99
19.800
7.875
266
53.200
9.827
433
86.600
17.715
100
20.000
7.913
267
53.400
9.828
434
86.800
17.727
101
20.200
7.951
268
53.600
9.829
435
87.000
17.738
102
20.400
7.989
269
53.800
9.830
436
87.200
17.748
103
20.600
8.026
270
54.000
9.831
437
87.400
17.758
104
20.800
8.063
271
54.200
9.832
438
87.600
17.767
105
21.000
8.100
272
54.400
9.833
439
87.800
17.776
106
21.200
8.136
273
54.600
9.834
440
88.000
17.784
156
107
21.400
8.172
274
54.800
9.835
441
88.200
17.792
108
21.600
8.208
275
55.000
9.836
442
88.400
17.799
109
21.800
8.244
276
55.200
9.837
443
88.600
17.805
110
22.000
8.279
277
55.400
9.838
444
88.800
17.812
111
22.200
8.314
278
55.600
9.839
445
89.000
17.817
112
22.400
8.348
279
55.800
9.840
446
89.200
17.823
113
22.600
8.382
280
56.000
9.841
447
89.400
17.828
114
22.800
8.416
281
56.200
9.842
448
89.600
17.833
115
23.000
8.450
282
56.400
9.843
449
89.800
17.838
116
23.200
8.483
283
56.600
9.844
450
90.000
17.842
117
23.400
8.515
284
56.800
9.845
451
90.200
17.846
118
23.600
8.547
285
57.000
9.846
452
90.400
17.850
119
23.800
8.579
286
57.200
9.847
453
90.600
17.854
120
24.000
8.611
287
57.400
9.848
454
90.800
17.857
121
24.200
8.642
288
57.600
9.849
455
91.000
17.861
122
24.400
8.673
289
57.800
9.850
456
91.200
17.864
123
24.600
8.703
290
58.000
9.851
457
91.400
17.867
124
24.800
8.733
291
58.200
9.852
458
91.600
17.869
125
25.000
8.762
292
58.400
9.853
459
91.800
17.872
126
25.200
8.791
293
58.600
9.854
460
92.000
17.874
127
25.400
8.819
294
58.800
9.855
461
92.200
17.877
128
25.600
8.847
295
59.000
9.856
462
92.400
17.879
129
25.800
8.875
296
59.200
9.857
463
92.600
17.881
130
26.000
8.902
297
59.400
9.858
464
92.800
17.882
131
26.200
8.929
298
59.600
9.859
465
93.000
17.884
132
26.400
8.955
299
59.800
9.860
466
93.200
17.885
133
26.600
8.981
300
60.000
9.876
467
93.400
17.887
134
26.800
9.006
301
60.200
9.905
468
93.600
17.888
135
27.000
9.030
302
60.400
9.936
469
93.800
17.889
136
27.200
9.054
303
60.600
9.969
470
94.000
17.890
157
137
27.400
9.078
304
60.800
10.004
471
94.200
17.890
138
27.600
9.101
305
61.000
10.041
472
94.400
17.891
139
27.800
9.124
306
61.200
10.079
473
94.600
17.892
140
28.000
9.146
307
61.400
10.119
474
94.800
17.892
141
28.200
9.167
308
61.600
10.160
475
95.000
17.892
142
28.400
9.188
309
61.800
10.203
476
95.200
17.892
143
28.600
9.209
310
62.000
10.248
477
95.400
17.892
144
28.800
9.228
311
62.200
10.294
478
95.600
17.893
145
29.000
9.248
312
62.400
10.341
479
95.800
17.894
146
29.200
9.266
313
62.600
10.390
480
96.000
17.895
147
29.400
9.284
314
62.800
10.441
481
96.200
17.896
148
29.600
9.302
315
63.000
10.493
482
96.400
17.897
149
29.800
9.319
316
63.200
10.546
483
96.600
17.898
150
30.000
9.335
317
63.400
10.601
484
96.800
17.899
151
30.200
9.351
318
63.600
10.657
485
97.000
17.900
152
30.400
9.366
319
63.800
10.714
486
97.200
17.901
153
30.600
9.380
320
64.000
10.773
487
97.400
17.902
154
30.800
9.394
321
64.200
10.833
488
97.600
17.903
155
31.000
9.407
322
64.400
10.894
489
97.800
17.904
156
31.200
9.420
323
64.600
10.956
490
98.000
17.905
157
31.400
9.432
324
64.800
11.019
491
98.200
17.906
158
31.600
9.444
325
65.000
11.084
492
98.400
17.907
159
31.800
9.455
326
65.200
11.150
493
98.600
17.908
160
32.000
9.466
327
65.400
11.216
494
98.800
17.909
161
32.200
9.477
328
65.600
11.284
495
99.000
17.910
162
32.400
9.486
329
65.800
11.353
496
99.200
17.911
163
32.600
9.496
330
66.000
11.422
497
99.400
17.912
164
32.800
9.505
331
66.200
11.493
498
99.600
17.913
165
33.000
9.513
332
66.400
11.565
499
99.800
17.914
166
33.200
9.522
333
66.600
11.637
500
100.000
17.914
158
Appendix F
Lab Cryostat Thermometry Codes
Figure F.1 shows the front panel of the SRS readout code. The configuration
panel shows the hardware settings: The GPIB address of the SIM900 mainframe is 2.
MUX 1 is installed in slot 2 of the mainframe; Diode monitor is in slot 1; MUX 2 is in
slot 8 and AC bridge is in slot 6. The readout code loops over all available channels
of MUX1 and MUX2 and produce real time plots. It also displays and saves all data
with time stamps. The block diagram of the readout code is shown in figure F.3.
Figure F.2 shows the front panel of the PID temperature controller. It consists
of six sub panels: the Lakeshore AC resistance bridge, the Keitheley current sources,
the Mechanical heat switch, the PID control, the file writing and a magnet current
display panel. In the Lakeshore AC bridge panel, the GPIB address is 12. There are
different excitation options available, because different thermometers require different
excitations in different temperature ranges. The germanium resistance temperature
(GRT) sensors require voltage excitation mode, while the ruthenium oxide (RuOx)
sensors require current excitation. There are two Keithley current sources, with GPIB
addresses of 22 and 24. Each can ramp up to 5 A. The ADR magnet allows a max
current of 9.0 A, and a max ramp rate of 0.01 A/s (0.005 A/s is recommended). A
basic ADR operation procedure is: (1)Close the heat switch and ramp both Keithley
1 and 2 up to 4.5 A; (2)Open the heat switch and ramp Keithley 2 down to 0; (3)Turn
on the PID control. In the control panel, the temperature set point and PID gains
can be changed. Block diagram is shown in figure F.4, F.5 and F.6.
159
Figure F.1: SRS readout program front panel.
Figure F.2: PID control program front panel.
160
Figure F.3: Block diagram of the SRS readout program.
161
Figure F.4: Block diagram of the PID control program. Part 1 of 3.
162
Figure F.5: Block diagram of the PID control program. Part 2 of 3.
163
Figure F.6: Block diagram of the PID control program. Part 3 of 3.
164
Bibliography
[1] Polarization
(waves).
Website
URLs,
2012.
http://en.wikipedia.org/wiki/Polarization_%28waves%29.
[2] C. L. Bennett, R. S. Hill, G. Hinshaw, M. R. Nolta, N. Odegard, L. Page,
D. N. Spergel, J. L. Weiland, E. L. Wright, M. Halpern, N. Jarosik, A. Kogut,
M. Limon, S. S. Meyer, G. S. Tucker, and E. Wollack. First-Year Wilkinson
Microwave Anisotropy Probe (WMAP) Observations: Foreground Emission.
Astrophys. J., Suppl. Ser., 148:97–117, September 2003.
[3] General
overview
of
sharc-ii.
Website
URLs,
2004.
http://www.submm.caltech.edu/~ sharc/.
[4] H. Li, C. D. Dowell, L. Kirby, G. Novak, and J. E. Vaillancourt. Design and
initial performance of SHARP, a polarimeter for the SHARC-II camera at the
Caltech Submillimeter Observatory. Applied Optics, 47:422–430, January 2008.
[5] M. S. Povich, J. M. Stone, E. Churchwell, E. G. Zweibel, M. G. Wolfire, B. L.
Babler, R. Indebetouw, M. R. Meade, and B. A. Whitney. A Multiwavelength
Study of M17: The Spectral Energy Distribution and PAH Emission Morphology of a Massive Star Formation Region. Astrophys. J., 660:346–362, May
2007.
[6] E. W. Pellegrini, J. A. Baldwin, C. L. Brogan, M. M. Hanson, N. P. Abel, G. J.
Ferland, H. B. Nemala, G. Shaw, and T. H. Troland. A Magnetically Supported
Photodissociation Region in M17. Astrophys. J., 658:1119–1135, April 2007.
165
[7] J. L. Dotson. Polarization of the Far-Infrared Emission from M17. Astrophys.
J., 470:566, October 1996.
[8] A. Schulz, R. Lenzen, T. Schmidt, and K. Proetel. Polarization of starlight in
M 17. Astron. Astrophys., 95:94–99, February 1981.
[9] J. E. Vaillancourt. Polarized Emission from Interstellar Dust. In M.-A. MivilleDeschênes & F. Boulanger, editor, EAS Publications Series, volume 23 of EAS
Publications Series, pages 147–164, 2007.
[10] Parameters of cosmology:
What wmap records.
Website URLs, 2010.
http://map.gsfc.nasa.gov/mission/sgoals_parameters_wmap.html.
[11] C. L. Bennett, M. Halpern, G. Hinshaw, N. Jarosik, A. Kogut, M. Limon,
S. S. Meyer, L. Page, D. N. Spergel, G. S. Tucker, E. Wollack, E. L. Wright,
C. Barnes, M. R. Greason, R. S. Hill, E. Komatsu, M. R. Nolta, N. Odegard,
H. V. Peiris, L. Verde, and J. L. Weiland. First-Year Wilkinson Microwave
Anisotropy Probe (WMAP) Observations: Preliminary Maps and Basic Results. Astrophys. J., Suppl. Ser., 148:1–27, September 2003.
[12] D. Larson, J. Dunkley, G. Hinshaw, E. Komatsu, M. R. Nolta, C. L. Bennett,
B. Gold, M. Halpern, R. S. Hill, N. Jarosik, A. Kogut, M. Limon, S. S. Meyer,
N. Odegard, L. Page, K. M. Smith, D. N. Spergel, G. S. Tucker, J. L. Weiland,
E. Wollack, and E. L. Wright. Seven-year Wilkinson Microwave Anisotropy
Probe (WMAP) Observations: Power Spectra and WMAP-derived Parameters.
Astrophys. J., Suppl. Ser., 192:16, February 2011.
[13] L. Page, G. Hinshaw, E. Komatsu, M. R. Nolta, D. N. Spergel, C. L. Bennett,
C. Barnes, R. Bean, O. Doré, J. Dunkley, M. Halpern, R. S. Hill, N. Jarosik,
A. Kogut, M. Limon, S. S. Meyer, N. Odegard, H. V. Peiris, G. S. Tucker,
L. Verde, J. L. Weiland, E. Wollack, and E. L. Wright. Three-Year Wilkinson
Microwave Anisotropy Probe (WMAP) Observations: Polarization Analysis.
Astrophys. J., Suppl. Ser., 170:335–376, June 2007.
166
[14] E. Komatsu, K. M. Smith, J. Dunkley, C. L. Bennett, B. Gold, G. Hinshaw,
N. Jarosik, D. Larson, M. R. Nolta, L. Page, D. N. Spergel, M. Halpern, R. S.
Hill, A. Kogut, M. Limon, S. S. Meyer, N. Odegard, G. S. Tucker, J. L. Weiland,
E. Wollack, and E. L. Wright. Seven-year Wilkinson Microwave Anisotropy
Probe (WMAP) Observations: Cosmological Interpretation. Astrophys. J.,
Suppl. Ser., 192:18, February 2011.
[15] C. L. Bennett et. al. MRI-R2 : Development of a Low-Frequency Microwave
Polarimeter for Large-Scale Surveys. In A Proposal submitted to the National
Science Foundation August 2009 in response to program solicitation number
NSF 09-561, 2009.
[16] Annual
variation
of
pwv
at
chajnantor.
Website
URLs,
2010.
http://www.apex-telescope.org/sites/chajnantor/atmosphere/pwvvar/.
[17] D. T. Chuss, E. J. Wollack, R. Henry, H. Hui, A. J. Juarez, M. Krejny, S. H.
Moseley, and G. Novak. Properties of a Variable-delay Polarization Modulator.
Applied Optics, 51(2):197–208, January 2012.
[18] G. L. James. Analysis and design of TE/11/-to-HE/11/ corrugated cylindrical
waveguide mode converters. IEEE Transactions on Microwave Theory Techniques, 29:1059–1066, October 1981.
[19] D. T. Chuss, C. L. Bennett, N. Costen, E. Crowe, K. Denis, J. R. Eimer,
N. Lourie, T. A. Marriage, S. H. Moseley, K. Rostem, T. R. Stevenson,
D. Towner, K. U-Yen, G. Voellmer, E. J. Wollack, and L. Zeng. Electromagnetic Design of Feedhorn-Coupled Transition-Edge Sensors for Cosmic Microwave Background Polarimetry. Journal of Low Temperature Physics, page
132, November 2011.
[20] K.D. Irwin and G.C. Hilton. Transition-edge sensors. In Christian Enss, editor,
Cryogenic Particle Detection, volume 99 of Topics in Applied Physics. Springer
Berlin / Heidelberg, 2005.
167
[21] Cryostat
model
104
olympus.
Website
URLs,
2010.
http://www.hpd-online.com/104_cryostat.php.
[22] Mce documents. Website URLs, 2012. http://e-mode.phas.ubc.ca/mcewiki/index.php
[23] J. L. Dotson, J. Davidson, C. D. Dowell, D. A. Schleuning, and R. H. Hildebrand. Far-Infrared Polarimetry of Galactic Clouds from the Kuiper Airborne
Observatory. Astrophys. J., Suppl. Ser., 128:335–370, May 2000.
[24] M. Houde, P. Bastien, J. L. Dotson, C. D. Dowell, R. H. Hildebrand, R. Peng,
T. G. Phillips, J. E. Vaillancourt, and H. Yoshida. On the Measurement of
the Magnitude and Orientation of the Magnetic Field in Molecular Clouds.
Astrophys. J., 569:803–814, April 2002.
[25] G. B. Rybicki and A. P. Lightman. Radiative processes in astrophysics. New
York, Wiley-Interscience, 1979. 393 p., 1979.
[26] A. Kogut, J. Dunkley, C. L. Bennett, O. Doré, B. Gold, M. Halpern, G. Hinshaw, N. Jarosik, E. Komatsu, M. R. Nolta, N. Odegard, L. Page, D. N. Spergel,
G. S. Tucker, J. L. Weiland, E. Wollack, and E. L. Wright. Three-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Foreground Polarization. Astrophys. J., 665:355–362, August 2007.
[27] D. P. Finkbeiner, M. Davis, and D. J. Schlegel. Extrapolation of Galactic
Dust Emission at 100 Microns to Cosmic Microwave Background Radiation
Frequencies Using FIRAS. Astrophys. J., 524:867–886, October 1999.
[28] L. Davis, Jr. and J. L. Greenstein. The Polarization of Starlight by Aligned
Dust Grains. Astrophys. J., 114:206, September 1951.
[29] D. C. B. Whittet, editor. Dust in the galactic environment, 2003.
[30] A. Lazarian. Magnetic Fields via Polarimetry: Progress of Grain Alignment
Theory. Journal of Quantitative Spectroscopy and Radiative Transfer, 79:881,
2003.
168
[31] A. Lazarian and T. Hoang. Radiative torques: analytical model and basic
properties. Mon. Not. R. Astron. Soc., 378:910–946, July 2007.
[32] W. G. Roberge. Alignment of Interstellar Dust. In A. N. Witt, G. C. Clayton, &
B. T. Draine, editor, Astrophysics of Dust, volume 309 of Astronomical Society
of the Pacific Conference Series, page 467, May 2004.
[33] E. M. Purcell. Suprathermal rotation of interstellar grains. Astrophys. J.,
231:404–416, July 1979.
[34] S. J. Barnett. Magnetization by Rotation. Physical Review, 6:239–270, October
1915.
[35] E. M. Purcell. Interstellar grains as pinwheels, pages 155–167. The Dusty
Universe, 1975.
[36] A. Z. Dolginov. Orientation of Interstellar and Interplanetary Grains. Astrophysics and Space Science, 18:337–349, October 1972.
[37] A. Z. Dolginov and I. G. Mytrophanov. Orientation of Cosmic Dust Grains (In
Russian). Astrophysics and Space Science, 43:257, 1976.
[38] B. T. Draine and J. C. Weingartner. Radiative Torques on Interstellar Grains.
I. Superthermal Spin-up. Astrophys. J., 470:551, October 1996.
[39] B. T. Draine and J. C. Weingartner. Radiative Torques on Interstellar Grains.
II. Grain Alignment. Astrophys. J., 480:633, May 1997.
[40] A. Lazarian and B. T. Draine. Disorientation of Suprathermally Rotating
Grains and the Grain Alignment Problem. Astrophys. J., 487:248, September
1997.
[41] A. Lazarian and B. T. Draine. Thermal Flipping and Thermal Trapping: New
Elements in Grain Dynamics. Astrophys. J., Lett., 516:L37–L40, May 1999.
[42] A. Lazarian and B. T. Draine. Nuclear Spin Relaxation within Interstellar
Grains. Astrophys. J., Lett., 520:L67–L70, July 1999.
169
[43] T. Gold. The alignment of galactic dust. Mon. Not. R. Astron. Soc., 112:215,
1952.
[44] J. Cho and A. Lazarian. Grain Alignment by Radiation in Dark Clouds and
Cores. Astrophys. J., 631:361–370, September 2005.
[45] C. Heiles. 9286 Stars: An Agglomeration of Stellar Polarization Catalogs. Astron. J., 119:923–927, February 2000.
[46] A. Berdyugin, V. Piirola, and P. Teerikorpi. Interstellar polarization at high
galactic latitudes from distant stars. VII. A complete map for southern latitudes
b < −70◦ . Astron. Astrophys., 424:873–876, September 2004.
[47] A. A. Goodman, T. J. Jones, E. A. Lada, and P. C. Myers. Does Near-Infrared
Polarimetry Reveal the Magnetic Field in Cold Dark Clouds? Astrophys. J.,
448:748, August 1995.
[48] H. G. Arce, A. A. Goodman, P. Bastien, N. Manset, and M. Sumner. The
Polarizing Power of the Interstellar Medium in Taurus. Astrophys. J., Lett.,
499:L93, May 1998.
[49] W. A. Hiltner. Polarization of Light from Distant Stars by Interstellar Medium.
Science, 109:165–+, February 1949.
[50] J. S. Hall. Observations of the Polarized Light from Stars. Science, 109:166–167,
February 1949.
[51] P. Fosalba, A. Lazarian, S. Prunet, and J. A. Tauber. Statistical Properties of
Galactic Starlight Polarization. Astrophys. J., 564:762–772, January 2002.
[52] B. Keating, P. Timbie, A. Polnarev, and J. Steinberger. Large Angular Scale
Polarization of the Cosmic Microwave Background Radiation and the Feasibility
of Its Detection. Astrophys. J., 495:580, March 1998.
170
[53] A. Kogut, A. J. Banday, C. L. Bennett, K. M. Gorski, G. Hinshaw, and W. T.
Reach. High-Latitude Galactic Emission in the COBE Differential Microwave
Radiometer 2 Year Sky Maps. Astrophys. J., 460:1, March 1996.
[54] A. de Oliveira-Costa, A. Kogut, M. J. Devlin, C. B. Netterfield, L. A. Page,
and E. J. Wollack. Galactic Microwave Emission at Degree Angular Scales.
Astrophys. J., Lett., 482:L17, June 1997.
[55] E. M. Leitch, A. C. S. Readhead, T. J. Pearson, and S. T. Myers. An Anomalous
Component of Galactic Emission. Astrophys. J., Lett., 486:L23, September
1997.
[56] S. R. Hildebrandt, R. Rebolo, J. A. Rubiño-Martı́n, R. A. Watson, C. M.
Gutiérrez, R. J. Hoyland, and E. S. Battistelli. COSMOSOMAS observations
of the cosmic microwave background and Galactic foregrounds at 11 GHz: evidence for anomalous microwave emission at high Galactic latitude. Mon. Not.
R. Astron. Soc., 382:594–608, December 2007.
[57] D. P. Finkbeiner. Microwave Interstellar Medium Emission Observed by the
Wilkinson Microwave Anisotropy Probe. Astrophys. J., 614:186–193, October
2004.
[58] R. A. Watson, R. Rebolo, J. A. Rubiño-Martı́n, S. Hildebrandt, C. M. Gutiérrez,
S. Fernández-Cerezo, R. J. Hoyland, and E. S. Battistelli. Detection of Anomalous Microwave Emission in the Perseus Molecular Cloud with the COSMOSOMAS Experiment. Astrophys. J., Lett., 624:L89–L92, May 2005.
[59] R. D. Davies, C. Dickinson, A. J. Banday, T. R. Jaffe, K. M. Górski, and
R. J. Davis. A determination of the spectra of Galactic components observed
by the Wilkinson Microwave Anisotropy Probe. Mon. Not. R. Astron. Soc.,
370:1125–1139, August 2006.
[60] G. Dobler, B. Draine, and D. P. Finkbeiner. Constraining Spinning Dust Parameters with the WMAP Five-Year Data. Astrophys. J., 699:1374–1388, July
2009.
171
[61] G. Dobler and D. P. Finkbeiner. Extended Anomalous Foreground Emission in
the WMAP Three-Year Data. Astrophys. J., 680:1222–1234, June 2008.
[62] B. T. Draine and A. Lazarian. Diffuse Galactic Emission from Spinning Dust
Grains. Astrophys. J., Lett., 494:L19, February 1998.
[63] B. T. Draine and A. Lazarian. Electric Dipole Radiation from Spinning Dust
Grains. Astrophys. J., 508:157–179, November 1998.
[64] Y. Ali-Haı̈moud, C. M. Hirata, and C. Dickinson. A refined model for spinning
dust radiation. Mon. Not. R. Astron. Soc., 395:1055–1078, May 2009.
[65] B. T. Draine and A. Lazarian. Magnetic Dipole Microwave Emission from Dust
Grains. Astrophys. J., 512:740–754, February 1999.
[66] A. de Oliveira-Costa, M. Tegmark, D. P. Finkbeiner, R. D. Davies, C. M.
Gutierrez, L. M. Haffner, A. W. Jones, A. N. Lasenby, R. Rebolo, R. J.
Reynolds, S. L. Tufte, and R. A. Watson. A New Spin on Galactic Dust.
Astrophys. J., 567:363–369, March 2002.
[67] S. Casassus, G. F. Cabrera, F. Förster, T. J. Pearson, A. C. S. Readhead, and
C. Dickinson. Morphological Analysis of the Centimeter-Wave Continuum in
the Dark Cloud LDN 1622. Astrophys. J., 639:951–964, March 2006.
[68] B. D. Savage and K. R. Sembach. Interstellar Abundances from Absorption-Line
Observations with the Hubble Space Telescope. Ann. Rev. Astron. Astrophys.,
34:279–330, 1996.
[69] K. R. Sembach and B. D. Savage. The Gas and Dust Abundances of Diffuse
Halo Clouds in the Milky Way. Astrophys. J., 457:211, January 1996.
[70] A. Lazarian and B. T. Draine. Resonance Paramagnetic Relaxation and Alignment of Small Grains. Astrophys. J., Lett., 536:L15–L18, June 2000.
172
[71] D. C. B. Whittet. Polarization of Starlight. In A. N. Witt, G. C. Clayton, &
B. T. Draine, editor, Astrophysics of Dust, volume 309 of Astronomical Society
of the Pacific Conference Series, page 65, May 2004.
[72] P. G. Martin. On Predicting the Polarization of Low Frequency Emission by
Diffuse Interstellar Dust. In M.-A. Miville-Deschênes & F. Boulanger, editor,
EAS Publications Series, volume 23 of EAS Publications Series, pages 165–188,
2007.
[73] D. K. Aitken, C. H. Smith, T. J. T. Moore, and P. F. Roche. Mid-infrared
polarization studies of SgrA: a three-dimensional study of the central parsec.
Mon. Not. R. Astron. Soc., 299:743–752, September 1998.
[74] A. G. G. M. Tielens. The Physics and Chemistry of the Interstellar Medium.
September 2005.
[75] R. M. Crutcher. Magnetic Fields in Molecular Clouds: Observations Confront
Theory. Astrophys. J., 520:706–713, August 1999.
[76] L. Mestel and P. A. Strittmatter. The magnetic field of a contracting gas cloudII. Finite diffusion effects-an illustrative example. Mon. Not. R. Astron. Soc.,
137:95, 1967.
[77] W. Cudlip, I. Furniss, K. J. King, and R. E. Jennings. Far infrared polarimetry
of W51A and M42. Mon. Not. R. Astron. Soc., 200:1169–1173, September 1982.
[78] R. H. Hildebrand, M. Dragovan, and G. Novak. Detection of submillimeter
polarization in the Orion nebula. Astrophys. J., Lett, 284:L51–L54, September
1984.
[79] S. R. Platt, R. H. Hildebrand, R. J. Pernic, J. A. Davidson, and G. Novak.
100-micron array polarimetry from the Kuiper Airborne Observatory - Instrumentation, techniques, and first results. Publ. Astron. Soc. Pac., 103:1193–1210,
November 1991.
173
[80] B. C. Matthews, C. A. McPhee, L. M. Fissel, and R. L. Curran. The Legacy
of SCUPOL: 850 µm Imaging Polarimetry from 1997 to 2005. Astrophys. J.,
Suppl. Ser., 182:143–204, May 2009.
[81] B. C. Matthews, C. A. McPhee, L. M. Fissel, and R. L. Curran. SCUPOL
Legacy polarimetry of SCUBA (Matthews+, 2009). VizieR Online Data Catalog, 218:20143, January 2010.
[82] D. A. Schleuning, C. D. Dowell, R. H. Hildebrand, S. R. Platt, and G. Novak.
HERTZ, A Submillimeter Polarimeter. Publ. Astron. Soc. Pac., 109:307–318,
March 1997.
[83] G. Novak, D. T. Chuss, J. A. Davidson, J. L. Dotson, C. D. Dowell, R. H.
Hildebrand, M. Houde, L. Kirby, M. Krejny, A. Lazarian, H.-b. Li, S. H.
Moseley, J. E. Vaillancourt, and F. Yusef-Zadeh. A polarimetry module for
CSO/SHARC-II. In C. M. Bradford, P. A. R. Ade, J. E. Aguirre, J. J. Bock,
M. Dragovan, L. Duband, L. Earle, J. Glenn, H. Matsuhara, B. J. Naylor,
H. T. Nguyen, M. Yun, & J. Zmuidzinas, editor, Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, volume 5498 of Society of
Photo-Optical Instrumentation Engineers (SPIE) Conference Series, pages 278–
289, October 2004.
[84] T.G. Phillips. The caltech submillimeter observatory. In Microwave Symposium,
2007. IEEE/MTT-S International, pages 1849 –1852, june 2007.
[85] M. Leong, R. Peng, M. Houde, H. Yoshida, R. Chamberlin, and T. G. Phillips.
A CSO submillimeter active optics system. In Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, volume 6275 of Society of
Photo-Optical Instrumentation Engineers (SPIE) Conference Series, July 2006.
[86] T. G. Phillips and D. P. Woody. Millimeter- and submillimeter-wave receivers.
Ann. Rev. Astron. Astrophys., 20:285–321, 1982.
[87] J. W. Kooi, R. A. Chamberlin, R. Monje, B. Force, D. Miller, and T. G. Phillips.
174
Technology Development for the Caltech Submillimeter Observatory Balanced
Receivers. ArXiv e-prints, January 2012.
[88] C. D. Dowell, C. A. Allen, R. S. Babu, M. M. Freund, M. Gardner, J. Groseth,
M. D. Jhabvala, A. Kovacs, D. C. Lis, S. H. Moseley, Jr., T. G. Phillips, R. F.
Silverberg, G. M. Voellmer, and H. Yoshida. SHARC II: a Caltech submillimeter
observatory facility camera with 384 pixels. In T. G. Phillips and J. Zmuidzinas, editors, Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, volume 4855 of Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, pages 73–87, February 2003.
[89] Sharp
-
the
sharc
ii
polarimeter.
Website
URLs,
2012.
http://lennon.astro.northwestern.edu/SHARP/instrument.html.
[90] E. Pascale, P. A. R. Ade, J. J. Bock, E. L. Chapin, J. Chung, M. J. Devlin,
S. Dicker, M. Griffin, J. O. Gundersen, M. Halpern, P. C. Hargrave, D. H.
Hughes, J. Klein, C. J. MacTavish, G. Marsden, P. G. Martin, T. G. Martin,
P. Mauskopf, C. B. Netterfield, L. Olmi, G. Patanchon, M. Rex, D. Scott,
C. Semisch, N. Thomas, M. D. P. Truch, C. Tucker, G. S. Tucker, M. P. Viero,
and D. V. Wiebe. The Balloon-borne Large Aperture Submillimeter Telescope:
BLAST. Astrophys. J., 681:400–414, July 2008.
[91] W. Holland, M. MacIntosh, A. Fairley, D. Kelly, D. Montgomery, D. Gostick, E. Atad-Ettedgui, M. Ellis, I. Robson, M. Hollister, A. Woodcraft,
P. Ade, I. Walker, K. Irwin, G. Hilton, W. Duncan, C. Reintsema, A. Walton, W. Parkes, C. Dunare, M. Fich, J. Kycia, M. Halpern, D. Scott, A. Gibb,
J. Molnar, E. Chapin, D. Bintley, S. Craig, T. Chylek, T. Jenness, F. Economou,
and G. Davis. SCUBA-2: a 10,000-pixel submillimeter camera for the James
Clerk Maxwell Telescope. In Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, volume 6275 of Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, July 2006.
175
[92] M. Nielbock, R. Chini, M. Jütte, and E. Manthey. High mass Class I sources
in M 17. Astron. Astrophys., 377:273–284, October 2001.
[93] B. C. Dunne, Y.-H. Chu, C.-H. R. Chen, J. D. Lowry, L. Townsley, R. A.
Gruendl, M. A. Guerrero, and M. Rosado. Diffuse X-Ray Emission from the
Quiescent Superbubble M17, the Omega Nebula. Astrophys. J., 590:306–313,
June 2003.
[94] L. K. Townsley, E. D. Feigelson, T. Montmerle, P. S. Broos, Y.-H. Chu, and
G. P. Garmire. 10 MK Gas in M17 and the Rosette Nebula: X-Ray Flows in
Galactic H II Regions. Astrophys. J., 593:874–905, August 2003.
[95] V. A. Gagen-Torn and N. V. Voshchinnikov. Polarization study of the nebula
NGC 6618 and neighboring stars. Astrofizika, 13:569–586, November 1977.
[96] R. H. Hildebrand. Magnetic fields and stardust. Quarterly Journal of the RAS,
29:327–351, September 1988.
[97] R. H. Hildebrand, J. L. Dotson, C. D. Dowell, D. A. Schleuning, and J. E. Vaillancourt. The Far-Infrared Polarization Spectrum: First Results and Analysis.
Astrophys. J., 516:834–842, May 1999.
[98] J. E. Vaillancourt. Analysis of the Far-Infrared/Submillimeter Polarization
Spectrum Based on Temperature Maps of Orion. Astrophys. J., Suppl. Ser.,
142:53–69, September 2002.
[99] R. Hildebrand and L. Kirby. Polarization of FIR/Sub-mm Dust Emission. In
A. N. Witt, G. C. Clayton, and B. T. Draine, editors, Astrophysics of Dust,
volume 309 of Astronomical Society of the Pacific Conference Series, page 515,
May 2004.
[100] J. E. Vaillancourt, C. D. Dowell, R. H. Hildebrand, L. Kirby, M. M. Krejny,
H.-b. Li, G. Novak, M. Houde, H. Shinnaga, and M. Attard. New Results on the
Submillimeter Polarization Spectrum of the Orion Molecular Cloud. Astrophys.
J., Lett., 679:L25–L28, May 2008.
176
[101] T. J. Bethell, A. Chepurnov, A. Lazarian, and J. Kim. Polarization of Dust
Emission in Clumpy Molecular Clouds and Cores. Astrophys. J., 663:1055–1068,
July 2007.
[102] B. T. Draine and A. A. Fraisse. Polarized Far-Infrared and Submillimeter Emission from Interstellar Dust. Astrophys. J., 696:1–11, May 2009.
[103] E. Hubble. A Relation between Distance and Radial Velocity among ExtraGalactic Nebulae. Proceedings of the National Academy of Science, 15:168–173,
March 1929.
[104] R. A. Alpher, H. Bethe, and G. Gamow. The Origin of Chemical Elements.
Physical Review, 73:803–804, April 1948.
[105] R. A. Alpher and R. C. Herman. On the Relative Abundance of the Elements.
Physical Review, 74:1737–1742, December 1948.
[106] M. Fumagalli, J. M. O’Meara, and J. X. Prochaska. Detection of Pristine Gas
Two Billion Years After the Big Bang. Science, 334:1245–, December 2011.
[107] F. Hoyle. A New Model for the Expanding Universe. Mon. Not. R. Astron.
Soc., 108:372, 1948.
[108] A. A. Penzias and R. W. Wilson. A Measurement of Excess Antenna Temperature at 4080 Mc/s. Astrophys. J., 142:419–421, July 1965.
[109] N. W. Boggess, J. C. Mather, R. Weiss, C. L. Bennett, E. S. Cheng, E. Dwek,
S. Gulkis, M. G. Hauser, M. A. Janssen, T. Kelsall, S. S. Meyer, S. H. Moseley,
T. L. Murdock, R. A. Shafer, R. F. Silverberg, G. F. Smoot, D. T. Wilkinson,
and E. L. Wright. The COBE mission - Its design and performance two years
after launch. Astrophys. J., 397:420–429, October 1992.
[110] E. Bertschinger. Simulations of Structure Formation in the Universe. Ann. Rev.
Astron. Astrophys., 36:599–654, 1998.
177
[111] A. H. Guth and S.-H. H. Tye. Phase Transitions and Magnetic Monopole
Production in the Very Early Universe. Physical Review Letters, 44:963, April
1980.
[112] A. H. Guth. Inflationary universe: A possible solution to the horizon and
flatness problems. Phys. Rev. D, 23:347–356, January 1981.
[113] A. A. Starobinsky. A new type of isotropic cosmological models without singularity. Physics Letters B, 91:99–102, March 1980.
[114] A. D. Linde. A new inflationary universe scenario: A possible solution of the
horizon, flatness, homogeneity, isotropy and primordial monopole problems.
Physics Letters B, 108:389–393, February 1982.
[115] A. Albrecht and P. J. Steinhardt. Cosmology for grand unified theories with
radiatively induced symmetry breaking. Physical Review Letters, 48:1220–1223,
April 1982.
[116] C. L. Chang. The Cryogenic Dark Matter Search (CDMS-II) experiment: First
results from the Soudan Mine. PhD thesis, Stanford University, California,
USA, 2005.
[117] A. Hime. SNOLAB - An International Facility for Underground Science. In
B. Cleveland, R. Ford, & M. Chen, editor, Topical Workshop on Low Radioactivity Techniques: LRT 2004., volume 785 of American Institute of Physics
Conference Series, pages 27–36, September 2005.
[118] P. Picchi and F. Pietropaolo. Physics projects for a future CERN-LNGS neutrino programme. Nuclear Physics B Proceedings Supplements, 77:187–197, May
1999.
[119] A. S. Murphy and Uk Dark Matter Collaboration. The Boulby Underground
Laboratory. In N. J. C. Spooner & V. Kudryavtsev, editor, The Identification
of Dark Matter, pages 453–459, April 2005.
178
[120] Lbne/Dusel Collaborations and C. Mariani. DUSEL (Deep Underground Science and Engineering Laboratory) and LBNE (Long Baseline Neutrino Experiment). Nuclear Physics B Proceedings Supplements, 217:344–346, August 2011.
[121] A. G. Riess, A. V. Filippenko, P. Challis, A. Clocchiatti, A. Diercks, P. M.
Garnavich, R. L. Gilliland, C. J. Hogan, S. Jha, R. P. Kirshner, B. Leibundgut,
M. M. Phillips, D. Reiss, B. P. Schmidt, R. A. Schommer, R. C. Smith, J. Spyromilio, C. Stubbs, N. B. Suntzeff, and J. Tonry. Observational Evidence from
Supernovae for an Accelerating Universe and a Cosmological Constant. Astron.
J., 116:1009–1038, September 1998.
[122] R. G. Crittenden and N. Turok. Looking for a Cosmological Constant with the
Rees-Sciama Effect. Physical Review Letters, 76:575–578, January 1996.
[123] S. Ho, C. Hirata, N. Padmanabhan, U. Seljak, and N. Bahcall. Correlation
of CMB with large-scale structure. I. Integrated Sachs-Wolfe tomography and
cosmological implications. Phys. Rev. D, 78(4):043519, August 2008.
[124] T. Giannantonio, R. Scranton, R. G. Crittenden, R. C. Nichol, S. P. Boughn,
A. D. Myers, and G. T. Richards. Combined analysis of the integrated SachsWolfe effect and cosmological implications. Phys. Rev. D, 77(12):123520, June
2008.
[125] J. H. Goldstein, P. A. R. Ade, J. J. Bock, J. R. Bond, C. Cantalupo, C. R.
Contaldi, M. D. Daub, W. L. Holzapfel, C. Kuo, A. E. Lange, M. Lueker,
M. Newcomb, J. B. Peterson, D. Pogosyan, J. E. Ruhl, M. C. Runyan, and
E. Torbet. Estimates of Cosmological Parameters Using the Cosmic Microwave
Background Angular Power Spectrum of ACBAR. Astrophys. J., 599:773–785,
December 2003.
[126] J. W. Fowler, V. Acquaviva, P. A. R. Ade, P. Aguirre, M. Amiri, J. W. Appel, L. F. Barrientos, E. S. Battistelli, J. R. Bond, B. Brown, B. Burger,
J. Chervenak, S. Das, M. J. Devlin, S. R. Dicker, W. B. Doriese, J. Dunkley,
179
R. Dünner, T. Essinger-Hileman, R. P. Fisher, A. Hajian, M. Halpern, M. Hasselfield, C. Hernández-Monteagudo, G. C. Hilton, M. Hilton, A. D. Hincks,
R. Hlozek, K. M. Huffenberger, D. H. Hughes, J. P. Hughes, L. Infante, K. D.
Irwin, R. Jimenez, J. B. Juin, M. Kaul, J. Klein, A. Kosowsky, J. M. Lau,
M. Limon, Y.-T. Lin, R. H. Lupton, T. A. Marriage, D. Marsden, K. Martocci, P. Mauskopf, F. Menanteau, K. Moodley, H. Moseley, C. B. Netterfield,
M. D. Niemack, M. R. Nolta, L. A. Page, L. Parker, B. Partridge, H. Quintana,
B. Reid, N. Sehgal, J. Sievers, D. N. Spergel, S. T. Staggs, D. S. Swetz, E. R.
Switzer, R. Thornton, H. Trac, C. Tucker, L. Verde, R. Warne, G. Wilson,
E. Wollack, and Y. Zhao. The Atacama Cosmology Telescope: A Measurement
of the 600 < ℓ < 8000 Cosmic Microwave Background Power Spectrum at 148
GHz. Astrophys. J., 722:1148–1161, October 2010.
[127] S. Das, T. A. Marriage, P. A. R. Ade, P. Aguirre, M. Amiri, J. W. Appel,
L. F. Barrientos, E. S. Battistelli, J. R. Bond, B. Brown, B. Burger, J. Chervenak, M. J. Devlin, S. R. Dicker, W. Bertrand Doriese, J. Dunkley, R. Dünner,
T. Essinger-Hileman, R. P. Fisher, J. W. Fowler, A. Hajian, M. Halpern,
M. Hasselfield, C. Hernández-Monteagudo, G. C. Hilton, M. Hilton, A. D.
Hincks, R. Hlozek, K. M. Huffenberger, D. H. Hughes, J. P. Hughes, L. Infante,
K. D. Irwin, J. Baptiste Juin, M. Kaul, J. Klein, A. Kosowsky, J. M. Lau,
M. Limon, Y.-T. Lin, R. H. Lupton, D. Marsden, K. Martocci, P. Mauskopf,
F. Menanteau, K. Moodley, H. Moseley, C. B. Netterfield, M. D. Niemack, M. R.
Nolta, L. A. Page, L. Parker, B. Partridge, B. Reid, N. Sehgal, B. D. Sherwin,
J. Sievers, D. N. Spergel, S. T. Staggs, D. S. Swetz, E. R. Switzer, R. Thornton,
H. Trac, C. Tucker, R. Warne, E. Wollack, and Y. Zhao. The Atacama Cosmology Telescope: A Measurement of the Cosmic Microwave Background Power
Spectrum at 148 and 218 GHz from the 2008 Southern Survey. Astrophys. J.,
729:62, March 2011.
[128] R. Keisler, C. L. Reichardt, K. A. Aird, B. A. Benson, L. E. Bleem, J. E.
Carlstrom, C. L. Chang, H. M. Cho, T. M. Crawford, A. T. Crites, T. de
Haan, M. A. Dobbs, J. Dudley, E. M. George, N. W. Halverson, G. P. Holder,
180
W. L. Holzapfel, S. Hoover, Z. Hou, J. D. Hrubes, M. Joy, L. Knox, A. T.
Lee, E. M. Leitch, M. Lueker, D. Luong-Van, J. J. McMahon, J. Mehl, S. S.
Meyer, M. Millea, J. J. Mohr, T. E. Montroy, T. Natoli, S. Padin, T. Plagge,
C. Pryke, J. E. Ruhl, K. K. Schaffer, L. Shaw, E. Shirokoff, H. G. Spieler,
Z. Staniszewski, A. A. Stark, K. Story, A. van Engelen, K. Vanderlinde, J. D.
Vieira, R. Williamson, and O. Zahn. A Measurement of the Damping Tail of the
Cosmic Microwave Background Power Spectrum with the South Pole Telescope.
Astrophys. J., 743:28, December 2011.
[129] M. Kamionkowski, A. Kosowsky, and A. Stebbins. A Probe of Primordial
Gravity Waves and Vorticity. Physical Review Letters, 78:2058–2061, March
1997.
[130] J. M. Kovac, E. M. Leitch, C. Pryke, J. E. Carlstrom, N. W. Halverson, and
W. L. Holzapfel. Detection of polarization in the cosmic microwave background
using DASI. Nature, 420:772–787, December 2002.
[131] QUIET Collaboration, C. Bischoff, A. Brizius, I. Buder, Y. Chinone, K. Cleary,
R. N. Dumoulin, A. Kusaka, R. Monsalve, S. K. Næss, L. B. Newburgh,
R. Reeves, K. M. Smith, I. K. Wehus, J. A. Zuntz, J. T. L. Zwart, L. Bronfman, R. Bustos, S. E. Church, C. Dickinson, H. K. Eriksen, P. G. Ferreira,
T. Gaier, J. O. Gundersen, M. Hasegawa, M. Hazumi, K. M. Huffenberger,
M. E. Jones, P. Kangaslahti, D. J. Kapner, C. R. Lawrence, M. Limon, J. May,
J. J. McMahon, A. D. Miller, H. Nguyen, G. W. Nixon, T. J. Pearson, L. Piccirillo, S. J. E. Radford, A. C. S. Readhead, J. L. Richards, D. Samtleben,
M. Seiffert, M. C. Shepherd, S. T. Staggs, O. Tajima, K. L. Thompson, K. Vanderlinde, R. Williamson, and B. Winstein. First Season QUIET Observations:
Measurements of Cosmic Microwave Background Polarization Power Spectra at
43 GHz in the Multipole Range 25 ≤ ℓ ≤ 475. Astrophys. J., 741:111, November
2011.
[132] S. M. Leach, A. R. Liddle, J. Martin, and D. J. Schwarz. Cosmological parame-
181
ter estimation and the inflationary cosmology. Phys. Rev. D, 66(2):023515, July
2002.
[133] H. V. Peiris, E. Komatsu, L. Verde, D. N. Spergel, C. L. Bennett, M. Halpern,
G. Hinshaw, N. Jarosik, A. Kogut, M. Limon, S. S. Meyer, L. Page, G. S. Tucker,
E. Wollack, and E. L. Wright. First-Year Wilkinson Microwave Anisotropy
Probe (WMAP) Observations: Implications For Inflation. Astrophys. J., Suppl.
Ser., 148:213–231, September 2003.
[134] V. A. Rubakov, M. V. Sazhin, and A. V. Veryaskin. Graviton creation in
the inflationary universe and the grand unification scale. Physics Letters B,
115:189–192, September 1982.
[135] Y. Zhao, C. Allen, M. Amiri, J. W. Appel, E. S. Battistelli, B. Burger, J. A.
Chervenak, A. J. Dahlen, S. Denny, M. J. Devlin, S. R. Dicker, W. B. Doriese,
R. Dünner, T. Essinger-Hileman, R. P. Fisher, J. W. Fowler, M. Halpern, G. C.
Hilton, A. D. Hincks, K. D. Irwin, N. Jarosik, J. Klein, J. M. Lau, T. A. Marriage, K. L. Martocci, S. H. Moseley, M. D. Niemack, L. Page, L. P. Parker,
A. Sederberg, S. T. Staggs, O. R. Stryzak, D. S. Swetz, E. R. Switzer, R. J.
Thornton, and E. J. Wollack. Characterization of transition edge sensors for
the Millimeter Bolometer Array Camera on the Atacama Cosmology Telescope.
In Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, volume 7020 of Society of Photo-Optical Instrumentation Engineers (SPIE)
Conference Series, August 2008.
[136] M. Kamionkowski, A. Kosowsky, and A. Stebbins. Statistics of cosmic microwave background polarization. Phys. Rev. D, 55:7368–7388, June 1997.
[137] J. Lazear, D. Benford, D. Chuss, D. Fixsen, J. Hinderks, G. Hinshaw, C. Jhabvala, B. Johnson, A. Kogut, P. Mirel, H. Mosely, J. Staghun, E. Wollack, A. Weston, K. Vlahacos, C. Bennett, J. Eimer, M. Halpern, K. Irwin, J. Dotson,
P. Ade, and C. Tucker. PIPER: Primordial Inflation Polarization Explorer. In
American Astronomical Society Meeting Abstracts 218, page 233.01, May 2011.
182
[138] T. E. Montroy, P. A. R. Ade, R. Bihary, J. J. Bock, J. R. Bond, J. Brevick,
C. R. Contaldi, B. P. Crill, A. Crites, O. Doré, L. Duband, S. R. Golwala,
M. Halpern, G. Hilton, W. Holmes, V. V. Hristov, K. Irwin, W. C. Jones, C. L.
Kuo, A. E. Lange, C. J. MacTavish, P. Mason, J. Mulder, C. B. Netterfield,
E. Pascale, J. E. Ruhl, A. Trangsrud, C. Tucker, A. Turner, and M. Viero. SPIDER: a new balloon-borne experiment to measure CMB polarization on large
angular scales. In Society of Photo-Optical Instrumentation Engineers (SPIE)
Conference Series, volume 6267 of Society of Photo-Optical Instrumentation
Engineers (SPIE) Conference Series, July 2006.
[139] P. Oxley, P. A. Ade, C. Baccigalupi, P. deBernardis, H.-M. Cho, M. J. Devlin, S. Hanany, B. R. Johnson, T. Jones, A. T. Lee, T. Matsumura, A. D.
Miller, M. Milligan, T. Renbarger, H. G. Spieler, R. Stompor, G. S. Tucker,
and M. Zaldarriaga. The EBEX experiment. In M. Strojnik, editor, Society
of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, volume
5543 of Society of Photo-Optical Instrumentation Engineers (SPIE) Conference
Series, pages 320–331, November 2004.
[140] P. L. Richards. Bolometers for infrared and millimeter waves. Journal of Applied
Physics, 76:1–24, July 1994.
[141] M. Bowden, A. N. Taylor, K. M. Ganga, P. A. R. Ade, J. J. Bock, G. Cahill,
J. E. Carlstrom, S. E. Church, W. K. Gear, J. R. Hinderks, W. Hu, B. G.
Keating, J. Kovac, A. E. Lange, E. M. Leitch, B. Maffei, O. E. Mallie, S. J.
Melhuish, J. A. Murphy, G. Pisano, L. Piccirillo, C. Pryke, B. A. Rusholme,
C. O’Sullivan, and K. Thompson. Scientific optimization of a ground-based
CMB polarization experiment. Mon. Not. R. Astron. Soc., 349:321–335, March
2004.
[142] D. Larson. Private Communication, 2010.
[143] S. Dodelson. Modern cosmology. Academic Press. ISBN 0-12-219141-2, 2003,
XIII + 440 p., 2003.
183
[144] J. R. Pardo, J. Cernicharo, and E. Serabyn. Atmospheric transmission at microwaves (ATM): an improved model for millimeter/submillimeter applications.
IEEE Transactions on Antennas and Propagation, 49:1683–1694, December
2001.
[145] H. J. Liebe. MPM - An atmospheric millimeter-wave propagation model. International Journal of Infrared and Millimeter Waves, 10:631–650, June 1989.
[146] J. R. Pardo, M. C. Wiedner, E. Serabyn, C. D. Wilson, C. Cunningham, R. E.
Hills, and J. Cernicharo. Side-by-Side Comparison of Fourier Transform Spectroscopy and Water Vapor Radiometry as Tools for the Calibration of Millimeter/Submillimeter Ground-based Observatories. Astrophys. J., Suppl. Ser.,
153:363–367, July 2004.
[147] J. C. Mather. Bolometer noise: nonequilibrium thoery. Applied Optics, 21:1125–
1129, March 1982.
[148] D. T. Chuss, P. A. R. Ade, D. J. Benford, C. L. Bennett, J. L. Dotson, J. R.
Eimer, D. J. Fixsen, M. Halpern, G. Hilton, J. Hinderks, G. Hinshaw, K. Irwin,
M. L. Jackson, M. A. Jah, N. Jethava, C. Jhabvala, A. J. Kogut, L. Lowe,
N. McCullagh, T. Miller, P. Mirel, S. H. Moseley, S. Rodriguez, K. Rostem,
E. Sharp, J. G. Staguhn, C. E. Tucker, G. M. Voellmer, E. J. Wollack, and
L. Zeng. The Primordial Inflation Polarization Explorer (PIPER). In Society
of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, volume
7741 of Society of Photo-Optical Instrumentation Engineers (SPIE) Conference
Series, July 2010.
[149] M. Krejny, D. Chuss, C. D. D’Aubigny, D. Golish, M. Houde, H. Hui, C. Kulesa,
R. F. Loewenstein, S. H. Moseley, G. Novak, G. Voellmer, C. Walker, and
E. Wollack. The Hertz/VPM polarimeter: design and first light observations.
Applied Optics, 47:4429, August 2008.
[150] D. T. Chuss, E. J. Wollack, S. H. Moseley, and G. Novak. Interferometric
polarization control. Applied Optics, 45:5107–5117, July 2006.
184
[151] G. M. Voellmer, C. Bennett, D. T. Chuss, J. Eimer, H. Hui, S. H. Moseley,
G. Novak, E. J. Wollack, and L. Zeng. A large free-standing wire grid for
microwave variable-delay polarization modulation. In Society of Photo-Optical
Instrumentation Engineers (SPIE) Conference Series, volume 7014 of Society
of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, August
2008.
[152] J. R. Eimer, C. L. Bennett, D. T. Chuss, and E. J. Wollack. Note: Vector reflectometry in a beam waveguide. Review of Scientific Instruments, 82(8):086101,
August 2011.
[153] J. R. Eimer, C. L. Bennett, D. T. Chuss, T. A. Marriage, E. J. Wollack, and
L. Zeng. The Cosmology Large Angular Scale Surveyor (CLASS): 40 GHz
optical design. in preparation, 2012.
[154] H. Tran and L. Page. Optical elements for a CMBPol mission. Journal of
Physics Conference Series, 155(1):012007, March 2009.
[155] D. J. Benford, M. C. Gaidis, and J. W. Kooi. Optical properties of Zitex in the
infrared to submillimeter. Applied Optics, 42:5118–5122, September 2003.
[156] L. Zeng, C. L. Bennett, D. T. Chuss, and E. J. Wollack.
A Low Cross-
Polarization Smooth-Walled Horn With Improved Bandwidth. IEEE Transactions on Antennas and Propagation, 58:1383–1387, April 2010.
[157] L. Zeng, C. L. Bennett, D. T. Chuss, and E. J. Wollack. A wide-band smoothwalled feedhorn with low cross polarization for millimeter astronomy. In Society
of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, volume
7741 of Society of Photo-Optical Instrumentation Engineers (SPIE) Conference
Series, July 2010.
[158] J. R. Pyle and R. J. Angley. Cutoff Wavelengths of Waveguides with Unusual
Cross Sections (Correspondence). IEEE Transactions on Microwave Theory
Techniques, 12:556–557, September 1964.
185
[159] P. S. Kildal. Foundations of Antennas: A Unified Approach. Studentlitteratur,
2000.
[160] W. H. Press, S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery. Numerical
recipes in C. The art of scientific computing. Cambridge: University Press,
—c1992, 2nd ed., 1992.
[161] H. Deguchi, M. Tsuji, and H. Shigesawa. Compact Low-Cross-Polarization Horn
Antennas With Serpentine-Shaped Taper. IEEE Transactions on Antennas and
Propagation, 52:2510–2516, October 2004.
[162] C. Granet, G. L. James, R. Bolton, and G. Moorey.
A Smooth-Walled
Spline-Profile Horn as an Alternative to the Corrugated Horn for Wide Band
Millimeter-Wave Applications. IEEE Transactions on Antennas and Propagation, 52:848–854, March 2004.
[163] M. Tinkham. Introduction to Superconductivity. McGraw-Hill, New York, USA,
1996.
[164] K. D. Irwin, M. D. Audley, J. A. Beall, J. Beyer, S. Deiker, W. Doriese, W. Duncan, G. C. Hilton, W. Holland, C. D. Reintsema, J. N. Ullom, L. R. Vale, and
Y. Xu. In-focal-plane SQUID multiplexer. Nuclear Instruments and Methods
in Physics Research A, 520:544–547, March 2004.
[165] P. J. B. Clarricoats and A. D. Oliver. Corrugated Horns for Microwave Antennas. Peter Peregrinus, Ltd., 1984.
[166] P. D. Potter.
A new horn antenna with suppressed sidelobes and equal
beamwidths. Journal of Physics Conference Series, pages 71–78, June 1963.
[167] E. Lier. Cross polarization from dual mode horn antennas. IEEE Transactions
on Antennas and Propagation, 34:106–110, January 1986.
[168] R. Turrin. Dual mode small-aperture antennas. IEEE Transactions on Antennas and Propagation, 15:307–308, March 1967.
186
[169] G. Ediss. Technical memorandum. Dual-mode horns at millimetre and submillimetre wavelengths. Microwaves, Antennas and Propagation, IEE Proceedings
H, 132:215–218, June 1985.
[170] H. M. Pickett, J. C. Hardy, and J. Farhoomand. Characterization of a dualmode horn for submillimeter wavelengths. IEEE Transactions on Microwave
Theory Techniques, 32:936, August 1984.
[171] S. P. Skobelev, B. J. Ku, A. V. Shishlov, and D. S. Ahn. Optimum geometry and
performance of a dual-mode horn modification. IEEE Antennas Propagation
Magazine, 43:90–93, August 2001.
[172] T. S. Bird. A Multibeam Feed for the Parkes Radio-telescope. IEEE Antennas
& Propagation Symposium, pages 966–969, March 1994.
[173] S. M. Tun and P. R. Foster. Computer optimised wideband and dual-mode
horn. Electronics Letters, pages 768–769, July 2001.
[174] G. Yassin, P. Kittara, A. Jiralucksanawong, S. Wangsuya, J. Leech, and
M. Jones. A High Performance Horn for Large Format Focal Plane Arrays.
In A. Karpov, editor, Eighteenth International Symposium on Space Terahertz
Technology, page 199, 2007.
[175] P. Kittara, A. Jiralucksanawong, G. Yassin, S. Wangsuya, and J. Leech. The
Design of Potter Horns for THz Applications Using a Genetic Algorithm. International Journal of Infrared and Millimeter Waves, 28:1103–1114, December
2007.
[176] J. M. Neilson. An improved multimode horn for Gaussian mode generation
at millimeter and submillimeter wavelengths. IEEE Transactions on Antennas
and Propagation, 50:1077–1081, August 2002.
[177] A. D. Olver, P. J. B Clarricoasts, A. A. Kishk, and L. Shafai. Microwave Horns
and Feeds. New York: IEEE Press, 1994.
187
[178] A. C. Ludwig. The definition of cross polarization. IEEE Transactions on
Antennas and Propagation, 21:116–119, 1973.
[179] E. J. Wollack.
TCHEBx : Homogeneous Stepped Waveguide Transformers
NRAO. EDTN Memo Series # 176, May 1996.
[180] J. L. Hesler, A. R. Kerr, W. Grammer, and E. Wollack. Recommendations for
Waveguide Interfaces to 1 THz. In A. Karpov, editor, Eighteenth International
Symposium on Space Terahertz Technology, page 100, 2007.
[181] D. J. Fixsen. Multimode antenna optimization. In R. Winston, editor, Society
of Photo-Optical Instrumentation Engineers (SPIE) Conference Series, volume
4446 of Society of Photo-Optical Instrumentation Engineers (SPIE) Conference
Series, pages 161–170, November 2001.
[182] D. J. Fixsen, E. S. Cheng, T. M. Crawford, S. S. Meyer, G. W. Wilson, E. S.
Oh, and E. H. Sharp. Lightweight long-hold-time Dewar. Review of Scientific
Instruments, 72:3112–3120, July 2001.
[183] W. Holzapfel and J. Ruhl. Private Communication, 2009.
188
Vita
Lingzhen Zeng was born in Laibin, Guangxi province, China, on 02 October 1982,
the son of Xiangxiong Zeng and Qiuying Li. After completing his work at No.1 High
School of Laibin, he went on to the University of Science and Technology of China
(USTC) in Hefei, Anhui province, China, where he studied astronomy and received
his Bachelor degree in July 2005. After that, he entered the department of physics and
astronomy at Johns Hopkins University (JHU) in Baltimore, Maryland as a graduate
student.
189