* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download 2.02 intersection of lines
Unification (computer science) wikipedia , lookup
Maxwell's equations wikipedia , lookup
Two-body Dirac equations wikipedia , lookup
BKL singularity wikipedia , lookup
Two-body problem in general relativity wikipedia , lookup
Debye–Hückel equation wikipedia , lookup
Schrödinger equation wikipedia , lookup
Dirac equation wikipedia , lookup
Van der Waals equation wikipedia , lookup
Navier–Stokes equations wikipedia , lookup
Euler equations (fluid dynamics) wikipedia , lookup
Computational electromagnetics wikipedia , lookup
Equations of motion wikipedia , lookup
Calculus of variations wikipedia , lookup
Itô diffusion wikipedia , lookup
Equation of state wikipedia , lookup
Differential equation wikipedia , lookup
Derivation of the Navier–Stokes equations wikipedia , lookup
Schwarzschild geodesics wikipedia , lookup
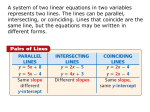
Name: 10/16/14 Geometry Unit 2 Finding the Intersection of Lines When two lines are in a plane, what different options arise? Example 1 (a) Write an equation for the line DE in slope-intercept form (b) Write an equation for the line FH, and get it into y-intercept form: (c) Use your equations for DE and FH to find out where they intersect. (_____, _____) Example 2: Example 2: Solve the following systems first by graphing, then algebraically. Check to see that your algebraic solution coincides with your graphical solution.! ! ! ! y= 1 x−3 2 ! 2y + x = -8! Algebraic solution:!! ! ! ! ! Graphical Solution:! ! ! ! ! ! ! ! ! ! ! First solve for y in equation 2, ! then graph both equations.! ! ! ! ! ! ! ! ! ! ! ! ! ! Answer: ( __ , __)! ! ! ! ! ! ! ! Example 3. Find the equation of the following lines.! A. ______________________________! ! ! ! ! ! ! ! ! B. ____________________________________! Example 4: Consider the system of equations! ! ⎧2y + 4x = 6 ⎨ " x + y =1 ! ⎩ ! A. Solve the system algebraically, using either the substitution or addition/elimination method.! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! ! B. Solve the first equation for y! to get in into y = mx + b form! ! ! ! x = _______ y = _______! ! ! ! ! ! ! y = ________________! D. Graph both equations and see! if their intersection agrees with your! algebraic answer.! ! ! C. Solve the second equation for y ! to get in into y = mx + b form! ! ! ! ! ! ! ! y = ________________! ! ! ! ! ! ! ! ! ! Name: 10/16/14 Unit 2 - Geometry HOMEWORK #2 – FINDING THE INTERSECTION OF LINES 1. Determine the point of intersection of the graphs of each system. Get each equation into y = mx + b form to graph! a) x + 2y = 7 x + y = 10 4x − y = 10 x − y = 2 b) Graphical: Graphical: Algebraic: Algebraic: (_____, _____) c) Solve y = 2x − 1 (_____, _____) d) y = 4x − 5 (_____, _____) x+y=6 y=5 x + 2y = 7 4x − y = 10 (_____, _____) Find the points of intersection of the following lines, using the addition/elimination method: 2. 8x + 5y = −13 3x − 2y = −1 ( ______ , ______ ) 3. Get equations for both lines in slope-intercept form, and then solve to find where they intersect. Equation for line AB in slope-intercept form: ________________________ Equation for line CD in slope-intercept form: ________________________ Find the coordinates of the point of intersection by solving the system: (_____, _____) 4. Write the following as coordinates: (a) x-intercept of 5 (___, ___) (b) y-intercept of –7 (____, ____) 5. Find the x and y intercepts (write them as coordinates!) for each line. (a) 5x – 6y = 30 (b) 15x + 10y - 60 = 0 x – int: x – int: y – int: y – int: Sketch: slope: slope: Equation: Equation: 6. Find the value of g that makes the following points collinear: (3, -6) (5, 1) (g, 12) g = ___________ 7. Find the coordinates of point B if M is the midpoint of segment AB with points A(3, -7) and M (4.5, 1) B ( ____, ____ )