Download Lecture 14

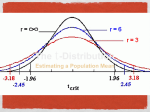
Applied Data Analysis
Spring 2017
Teenage Karen
Karen Albert
[email protected]
Thursdays, 4-5 PM (Hark 302)
Lecture outline
1. T-distribution
2. Two samples
What, if anything, is different about this problem?
A professor claims that an exam has a true mean of 70. 6 test
results turn out to be:
72, 79, 65, 84, 67, 77
What conclusion would you draw about the professor’s claim?
The sample size is small so we cannot rely on the central limit
theorem.
Problem solved in the service of great beer
The t-distribution was invented by W.S. Gossett (1876-1936)
while working for Guinness Brewery. He wanted to test a small
number of bottles off the production line for quality control
purposes.
He published under the name “Student” so his trade secret
would be protected. Thus, the t-distribtuion is sometimes
known as Student’s distribution.
Next time you’re in Dublin
The t-distribution versus the Normal
t-distribution
1. The t distribution is bell shaped and symmetric about 0.
t-distribution
1. The t distribution is bell shaped and symmetric about 0.
2. The width of the t-distribution depends on the degrees of
freedom.
t-distribution
1. The t distribution is bell shaped and symmetric about 0.
2. The width of the t-distribution depends on the degrees of
freedom.
3. For inference about a population mean, the degrees of
freedom are n − 1.
t-distribution
1. The t distribution is bell shaped and symmetric about 0.
2. The width of the t-distribution depends on the degrees of
freedom.
3. For inference about a population mean, the degrees of
freedom are n − 1.
4. The t-distribution has thicker tails and is more spread out
than the standard normal.
What is a degree of freedom?
It is simply the name given to the parameter of the t-distribution.
Normal distributions have different means and standard
deviations.
t-distributions do not have means or standard deviations; they
have degrees of freedom.
How to use the t-table
How to use the t-table
pt(1.53,4,lower.tail=FALSE)
## [1] 0.1003793
We need a new standard error
When we don’t know the S.D. of the box, and the number of
measurements is small, our usual estimate is likely to be off.
We need a new standard error
When we don’t know the S.D. of the box, and the number of
measurements is small, our usual estimate is likely to be off.
So we divide the standard deviation by slightly less,
s.e. = √
s
n−1
Example
A professor claims that an exam has a true mean of 70. 6 test
results turn out to be:
72, 79, 65, 84, 67, 77
x <- c(72,79,65,84,67,77)
xbar <- mean(x)
xbar
## [1] 74
sd <- sqrt(sum((x-xbar)^2/(length(x))))
sd
## [1] 6.683313
What conclusion would you draw about the professor’s claim?
Answer
t
74 − 70
√
6.68/ 5
≈ 1.34
=
t <- (xbar-70)/(sd/sqrt(length(x)-1))
t
## [1] 1.338299
pt(t,5,lower.tail=FALSE)
## [1] 0.1192149
Answer part deux
The probability being greater than 70 is about 12%.
Another way
ttest <- t.test(x,alternative="greater",mu=70)
ttest
##
##
##
##
##
##
##
##
##
##
##
One Sample t-test
data: x
t = 1.3383, df = 5, p-value = 0.1192
alternative hypothesis: true mean is greater than 70
95 percent confidence interval:
67.97729
Inf
sample estimates:
mean of x
74
The p-value is fairly large so we would fail to reject the null
hypothesis.
When to use the t-distribution
• The data are like draws from a box.
• The S.D. of the box is unknown.
• The number of observations is small, so the SD of the box
cannot be accurately estimated.
• The histogram for the contents of the box does not look too
different from the normal curve.
The t-distribution when n − 1 is large
pt(-1,5,lower.tail=TRUE)
## [1] 0.1816087
pt(-1,30,lower.tail=TRUE)
## [1] 0.1626543
pnorm(-1,0,1,lower.tail=TRUE)
## [1] 0.1586553
Confidence intervals with t
Given the following GPAs for 6 students:
2.80, 3.20, 3.75, 3.10, 2.95, 3.40
Calculate a 95% confidence interval for the mean GPA.
Solution, part 1
x <- c(2.80, 3.20, 3.75, 3.10, 2.95, 3.40)
xbar <- mean(x)
xbar
## [1] 3.2
sd <sd
sqrt(sum((x-xbar)^2/(length(x))))
## [1] 0.3095696
se <- sd/sqrt(length(x)-1)
se
## [1] 0.1384437
qt(.975,5)
## [1] 2.570582
Solution, part 2
x̄ ± t1− α2 ∗ SE
3.2 ± 2.57(0.138)
[2.84, 3.56]
Or....
ttest <- t.test(x,alternative="two.sided",mu=3.2)
ttest
##
##
##
##
##
##
##
##
##
##
##
One Sample t-test
data: x
t = 0, df = 5, p-value = 1
alternative hypothesis: true mean is not equal to 3.2
95 percent confidence interval:
2.844119 3.555881
sample estimates:
mean of x
3.2
New problem
Cycle II of the Health Examination Survey used a nationwide
probability sample of children age 6 to 11. One object of the
survey was to study the relationship between the children’s
scores of intelligence tests and family backgrounds. The WISC
vocabulary scale was used. This consists of 400 words that the
child has to define: 2 points for a correct answer, and 1 point for
a partially correct answer.
Continued
There was some relationship between tests scores and the
type of community in which the parents lived. For example,
big-city children averaged 26 points on the tests, and the SD
was 10 points. Rural children average 25 points with the same
SD. Can the difference be explained as chance variation?
Assume the investigators took a SRS of 400 big-city children
and an independent SRS of 400 rural children.
Comparing independent samples
Now we have two boxes.
One hundred draws are made at random with replacement from
box A, which contains (2, 4, 6, 8, 10), and independently, 100
draws are made at random with replacement from box B, which
contains (1, 3, 6, 9, 11).
Comparing independent samples
Now we have two boxes.
One hundred draws are made at random with replacement from
box A, which contains (2, 4, 6, 8, 10), and independently, 100
draws are made at random with replacement from box B, which
contains (1, 3, 6, 9, 11).
What is the expected value and the S.E. for the difference
between the mean of box A and the mean of box B?
The expected value
The parameter we are trying to estimate is
µA − µB
and the estimator is
x̄A − x̄B
The expected value
The parameter we are trying to estimate is
µA − µB
and the estimator is
x̄A − x̄B
We expect the sample mean of the draws from box A to be
about 6.
The expected value
The parameter we are trying to estimate is
µA − µB
and the estimator is
x̄A − x̄B
We expect the sample mean of the draws from box A to be
about 6.
We also expect the sample mean of the draws from box B to be
about 6.
The expected value
The parameter we are trying to estimate is
µA − µB
and the estimator is
x̄A − x̄B
We expect the sample mean of the draws from box A to be
about 6.
We also expect the sample mean of the draws from box B to be
about 6.
The sampling distribution of x̄A − x̄B thus has expectation
µA − µB or 0.
The standard error
The standard deviation of box A is about 3.2.
The standard deviation of box B is about 4.1.
The standard error
The standard deviation of box A is about 3.2.
The standard deviation of box B is about 4.1.
The standard error for the mean of each of the boxes is
S.E.x̄A
=
S.E.x̄B
=
3.2
√
= 0.32
100
4.1
√
= 0.41
100
The standard error
The standard deviation of box A is about 3.2.
The standard deviation of box B is about 4.1.
The standard error for the mean of each of the boxes is
S.E.x̄A
=
S.E.x̄B
=
3.2
√
= 0.32
100
4.1
√
= 0.41
100
What about the standard error for the difference?
S.E. for the difference
When the draws are independent, we can use the square root
law, which says that the standard error for the difference
between two independent quantities is
p
a2 + b 2
where a is the S.E. for the first quantity and b is the S.E. for the
second quantity.
S.E. for the difference
The S.E. we are looking for then is
SE
q
S.E.2A + S.E.2B
=
S.E. for the difference
The S.E. we are looking for then is
SE
q
S.E.2A + S.E.2B
=
s
3.2 2
4.1 2
=
+
10
10
S.E. for the difference
The S.E. we are looking for then is
SE
q
S.E.2A + S.E.2B
=
s
3.2 2
4.1 2
=
+
10
10
p
=
0.322 + 0.412
S.E. for the difference
The S.E. we are looking for then is
SE
q
S.E.2A + S.E.2B
=
s
3.2 2
4.1 2
=
+
10
10
p
=
0.322 + 0.412
= 0.52
S.E. for the difference
In general, the S.E. for the mean difference is
s
SEx̄1 −x̄2 =
s12
s2
+ 2
n1 n2
Back to the problem
There was some relationship between tests scores and the
type of community in which the parents lived. For example,
big-city children averaged 26 points on the tests, and the SD
was 10 points. Rural children average 25 points with the same
SD. Can the difference be explained as chance variation?
Assume the investigators took a SRS of 400 big-city children
and an independent SRS of 400 rural children.
The hypotheses
The null hypothesis is that the difference between the true
means is 0:
H0 : µbc − µr = 0
The hypotheses
The null hypothesis is that the difference between the true
means is 0:
H0 : µbc − µr = 0
Note that we could also write
H0 : µbc = µr
The hypotheses
The null hypothesis is that the difference between the true
means is 0:
H0 : µbc − µr = 0
Note that we could also write
H0 : µbc = µr
The alternative is
H1 : µbc 6= µr
S.E.
The standard error for the mean difference is
s
SEx̄1 −x̄2
=
s12
s2
+ 2
n1 n2
S.E.
The standard error for the mean difference is
SEx̄1 −x̄2
s
s12
s2
+ 2
n1 n2
r
102
102
+
400 400
=
=
S.E.
The standard error for the mean difference is
s
SEx̄1 −x̄2
=
r
s12
s2
+ 2
n1 n2
102
102
+
√ 400 400
=
0.25 + 0.25
=
S.E.
The standard error for the mean difference is
s
SEx̄1 −x̄2
=
s12
s2
+ 2
n1 n2
r
102
102
+
√ 400 400
=
0.25 + 0.25
=
≈ 0.7
Interpret the S.E.
0.7 is roughly the average distance of the sample
mean differences (x̄1 − x̄2 ) from the true, but unknown,
mean difference (µ1 − µ2 ).
The test statistic
As always, it is the observed minus the expected divided by the
standard error:
(26 − 25) − 0
0.7
≈ 1.4
z =
The test statistic
As always, it is the observed minus the expected divided by the
standard error:
(26 − 25) − 0
0.7
≈ 1.4
z =
2*pnorm(1.4,0,1,lower.tail=FALSE)
## [1] 0.1615133
Remember that this is a two-tailed test. The p-value is then
16% so we fail to reject the null hypothesis. The difference
could be due to chance.
What did we learn?
• The connection between the t-distribution and beer.
• Inference for two independent samples.