Download Chapter 7 - Haiku Learning

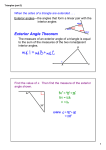
Chapter 7
Although not very common in the natural world, the idea of parallel lines has great
importance for the world that humankind has constructed. For example, when a
building is being put up, the beams that support the floors must be parallel.
183
Chapter
7
Focus on Skills
ALGEBRA
Complete.
1. If a, b, and care all greater than zero and a = b + c, then • is the
greatest of the three numbers.
2. If x + a = y and x + b = y, then •
3. If c = d and d = e, then •
= • .
= • .
Solve each equation.
4. 5x - 1 = 2x + 5
6. 6t - 24 = 4t + 14
5. (2x + 5) + (7x - 14)
7. 135 = 71 + z
= 180
9. (p - 2)180 = 3,780
8. b + 43 + 82 = 180
GEOMETRY
Sketch a figure to match each description. Mark all parallel sides, all
congruent sides, and any right angles.
11. a rhombus that is not a rectangle
10. a rectangle that is not a square
13. a parallelogram that is not a rectangle
12. a trapezoid with no congruent sides
Draw a figure similar to, but larger than, the one shown and construct
the indicated figure.
15. a triangle congruent to ~ABC
L1
14. L2 with vertex Q such that L2
=
L
A
Q
16. a perpendicular to k through P
~k
B~C
17. a perpendicular to j through M
~j
PROBLEM SOLVING
18. In ~RST, mLT = 3 • mLR, mLS = 2 • mLR, and
mLR + mLS + mLT= 180°. Find the measure of each angle.
184
Chapter 7 Focus on Skills
7.1
Transversals and Angles
Objective: To identify the angles formed when two lines are cut by a
transversal.
In the- next several lessons, you will discover some properties of the angles
that are formed when parallel lines are intersected by other lines.
EXPLORING
1. Draw two lines a and b. Draw a third line t that intersects
a and b in different points. Label the angles as shown.
2. Classify the angles as acute, right, or obtuse.
3. Must any of the numbered angles be congruent? Why?
4. Must any of the numbered angles be supplementary? Why?
A transversal is a line that intersects two or more
lines, each at a different point. Line t 1 is a transversal,
but t2 is not.
In the figure at the right, four of the numbered angles
are interior angles inside lines a and b. Four are
exterior angles outside lines a and b.
Line t is a transversal for lines a and b.
L3, L4, L5, and L6 are interior angles.
L 1, L2, L7, and L8 are exterior angles.
Certain pairs of angles determined by a transversal have special names.
Alternate interior angles
Corresponding angles
• are interior angles
• consist of one interior and one exterior angle
• are on opposite sides of the transversal
• are on the same side of the transversal
• have different vertices
• have different vertices
7.1 Transversals and Angles
185
Exam pie: Name all interior angles, exterior angles,
vertical angles, corresponding angles, and
alternate interior angles.
Solution: Interior angles: L2, L3, L6, L7
Exterior angles: Ll , L4, L5, L8
Vertical angles: Ll and L7, L2 and L8, L3 and L5 , L4 and L6
Corresponding angles: Ll and L3, L2 and L4, L5 and L7, L6 and L8
Alternate interior angles: L2 and L6, L3 and L7
Look at the figure shown. Which pairs of angles on the
same side of the transversal do you think should be
called same-side interior angles? same-side exterior
angles? Explain your answers.
Class Exercises
Name each of the following.
1. a transversal
2. four interior angles
3. four exterior angles
4. four pairs of vertical angles
5. four pairs of corresponding angles
6. two pairs of alternate interior angles
7. two pairs of same-side interior angles
8. two pairs of same-side exterior angles
Exercises
Name each of the following.
1. four interior angles
2. four exterior angles
3. two pairs of alternate interior angles
4. four pairs of corresponding angles
S·.J four pairs of vertical angles
186
Chapter 7 Parallel Lines
m
N arne each of the following.
6.
7.
8.
9.
10.
s
four interior angles along transversal m
four exterior angles along transversal r
9 110
12 111
two pairs of alternate interior angles along transversal s
13 114
16 115
two pairs of alternate interior angles along transversal/
four pairs of corresponding angles along transversal/
11. two pairs of same-side interior angles along transversal r
12. two pairs of same-side exterior angles along transversal m
Classify each pair of angles as (a) alternate interior angles,
(b) corresponding angles, (<e)_vertical angles, (d) same-side
interior angles, ~adjacent supplementary angles, or
~one of the above.
13. L2 and L8
14. L2 and L6
15. L4 and L5
16. L5 and L7
17. L6 and L7
18. Ll and L3
3 6
19. Ll and L6
20. L2 and L7
4 15
1 I8
2/7
•
Name the segments and transversal that determine each pair of
alternate interior angles.
21. a. Ll and L2
VY.
D
C
E.,.
22. a. Ll and L4
b. L3 and L4
c. L5andL6
~3 7
A
B
d. Ll and L7
~----...,.....-----,
T
b.L2 and L3
c. L5 and L8
d. L6 and L7
R
v
~
'
"-
1
APPLICATION
23. Linguistics Use a dictionary to find the meanings of correspond
and transverse that are related to this lesson.
Seeing in Geometry
Narne all pairs of corresponding angles determined
by AB and CF and transversal RW.
7.1 Transversals and Angles
187
7.2
Parallel Lines and
Interior Angles
Objective: To use relationships between interior angles and parallel lines.
When two lines are parallel and are cut by a transversal, certain relationships
exist among the eight angles that are formed. In this lesson and Lesson 7 .3,
you will learn about those relationships.
EXPLORING
1. Use the two edges of a ruler to draw two parallel lines. Then draw
any transversal t. Label the interior angles as shown.
2. Use a protractor to measure L1, L2, L3, and L4. Which pairs of
angles are congruent? Which are supplementary?
3. Repeat Steps 1 and 2 using a different pair of parallel lines and a
different position for the transversal. Do you get the same results?
The EXPLORING activity demonstrates the following.
POSTULATE 9 (Alternate Interior Angles Postulate): If two
parallelliges are cut by a transversal, then each pair of alternate
interior angles are congruent.
THEOREM 7.1 (Same-Side Interior Angles Theorem): If two
parallel lines are cut by a transversal, then each pair of same-side
interior angles are supplementary.
127c
Example 1: Find the measure of each numbered angle.
a.
b.
30°
A
Solution: a. mL1
=75°
mL2 = 105°
mL3 = 105°
188
Chapter 7
Parallel Lines
20o
D
b. Since BC II AD, mL4 = 20°.
Since AB II DC, mL5 = 30°.
EXPLORING
1. Draw two intersecting lines t and c. Label L1 and
point P on line t as shown.
2. Using a protractor and a straightedge, draw line d
through point P so that L 1 and L2 are congruent
alternate interior angles.
3. What is mL2 + mL3? What is mL 1 + mL3? Why?
4. Describe the relationship between L1 and L3 .
5. What seems to be the relationship between lines c and d?
+
*
3
c
POSTULATE 10: If two lines are cut by a transversal so that one
pair of alternate interior angles are congruent, then the lines are
parallel.
THEOREM 7.2: If two lines are cut by a transversal so that one
pair of same-side interior angles are supplementary, then the lines are
parallel.
Example 2: Tell whether the lines shown are parallel.
a.~
65 °
65 o
c.
b.
•
•
m
a
Solution: a. /II m
b. a II b
2. Tell how the measures of each pair of angles are related.
b. LB and LC
e. LA and LC
911
89°
c. m is not parallel to n
1. If Pis a point not on line c, how many lines parallel to c can be drawn
through Pin a plane?
a. LA and LB
d. LA and LD
m
•n
•
c. LC and LD
f. LB and LD
A
c
lc
B
3. RSTW is a parallelogram. LR is a right angle.
a. What is mLS? Why?
b. What are mLTand mLW?
7.2 Parallel Lines and Interior Angles
189
Class Exercises
Name each of the following.
1. an angle congruent to L 1
2. an angle congruent to L4
3. two angles supplementary to L2
4. two angles supplementary to L3
Find the measure of each angle.
5. L1
6. L2
7. L3
9. L5
8. L4
10. L6
11. L7
12. L8
Exercises
Name each of the following.
1.
2.
3.
4.
an angle congruent to L 1
an angle congruent to L 4
two angles supplementary to L2
two angles supplementary to L3
d
Find the measure of each angle.
5. L1
6. L2
7. L ·3
8. L4
9. L5
10. L6
11. L7
12. L8
•
ill(
1 · - ,._.
)
- ....
-,
-,
•
a
..
b
13. a. Name two pairs of alternate interior angles.
b. N arne two pairs of same-side interior angles.
=
=, ,
c. If L1
U , then lll m.
d. If mL 1 + m ~ = 180°, then l II m.
e. If L2
then l II m.
m
Find the measure of each angle.
15. EHGF is a parallelogram.
14. PMRQ is a parallelogram.
::~~
c. LR
190
P
l
50
Chapter 7
/R
Q
Parallel Lines
a.LHEF ~G
b. LHEG
c. LHGE E
15o
F
16. DABC is a parallelogram.
a. LCDA
b. L1
c. L2
17. a. L1
A
\/ \
D
d. L3
b. L2
c. L3
d. L4
c
18. RECT is a rectangle.
a. L1
T
b. L2
c. L3
R
19. a. L1
C2J
2
b. L2
C
lvv
- ~~
---::::> E
1
c. L3
E
D
Name the segments or lines that must be parallel.
20.
Q
D
60°
21.
A
H
22.
•n
~m
X
u
--
,------:----:;JT
pv
-''-'
'
89°
91 °
89°
91 °
y
~
Name the lines, if any, that must be parallel if each
statement is true.
23. L1 ::: L2
24. mL1 + mL3 = 180°
25. mL3 + mL5 = 180°
26. L2 ::: L4
27. mL2 + mL3 = 180°
28. L4::: L5
=
29. If L4 L6 and L8
be parallel.
=L10, name all lines that must
30. If a II band b II c, must line a be parallel to line c? Explain.
APPLICATIONS
Find the measure of each indicated angle.
31. Algebra
LABC and LBCD
32. Algebra
E
LEFG and LFGH
(3x + 20) 0
7.2 Parallel Lines and Interior Angles
191
Find the measure of each indicated angle.
33. Algebra LRST, LPTS, and LSTR
34. Algebra
LJ, LK, and LL
,.------.-::--::------:""' T
s
K::
,_n
. . . _,,.
/
Are the indicated segments parallel? Explain.
35. Logic AB and DC
36. Logic
B
R
RW and ST
(6y- 5) 0
K
J
]
~ _,
T
Historical Note
The following statement is equivalent to our Postulates 9 and 10.
Given a line land a point P not on l, there is
exactly one line through P that is parallel to l.
p
~------ · -------------~
Although this statement, known as The Parallel Postulate, may seem
obvious, mathematicians tried for more than 2,000 years to prove it. In the
early 1800s, two mathematicians, Janos Bolyai of Hungary and Nicolai
Lobachevsky of Russia, independently made the same discovery: The
assumption that there is more than one line through P that is parallel to l
does not lead to a contradiction. In fact, the mathematicians developed a
new geometry based on the assumption that an infinite number of lines
through P are parallel to l.
During the same period, the German mathematician Georg Riemann '
developed another geometry based on the assumption that there are no
lines passing through P that are parallel to l.
192
Chapter 7
Parallel Lines
7.3 Parallel Lines and
Corresponding Angles
Objective: To use facts about parallel lines cut by a transversal and pairs
of corresponding angles.
In this lesson, you will learn more about how the fact that two lines are
parallel relates to the congruence between certain angles formed by a
transversal.
EXPLORING
The measure of L1
=50°.
1. Find the measures of L2, L3, and L4.
2. What is the measure of L6? Why?
3. Find the measures of L5, L7, and L8.
4. Name all pairs of corresponding angles. Compare
the measures of corresponding angles.
The EXPLORING activity demonstrates the following theorem.
THEOREM 7.3 (Corresponding Angles Theorem): Iftwo
parallel lines are cut by a transversal, then each pair of corresponding
angles are congruent.
EXPLORING
1. Enter and run the following LOGO
program.
To transversal
fd 50 bk 100 fd 50
rt 40
fd 50 bk 100 fd 50
fd 20 It 25
fd 50 bk 100 fd 50
end
)$ill
JJ:S:Im:l~
2. Are the first and third lines created by
the turtle parallel? If not, what must
you change to make the turtle draw the
third line parallel to the first line?
Make the change( s). Run the new
program.
7.3 Parallel Lines and Corresponding Angles
193
The EXPLORING activity demonstrates the following theorem.
THEOREM 7.4: If two lines are cut by a transversal so that one
pair of corresponding angles are congruent, then the lines are parallel.
Example: a. Name the lines, if any, that must be parallel.
b. Find the measure of L1.
Solution: a. Since corresponding angles 2 and 3 are both
right angles, e II f (Notice that since
mL3 :;:. 89°, lines c and dare not parallel.)
b. Since e II f, mLl = 89°.
d
c
89°
6
e
131
f
A statement that follows directly from a theorem is sometimes called a
corollary. Part (a) of the Example demonstrates the following corollary
of Theorem 7 .4.
COROLLARY: If two coplanar lines are perpendicular to a third
line, then the two lines are parallel to each other.
1. Describe four methods of showing that two lines are parallel.
2. Explain in your own words the difference between the Corresponding
Angles Theorem and Theorem 7.4.
Class Exercises
Name each of the following.
1. four pairs of corresponding angles
2. three angles congruent to L2
3. three angles congruent to L5
Find the measure of each numbered angle.
4. Ll
5. L2
6. L3
7. L4
8.'L5
9. L6
10. L7
11. L8
194
Chapter 7 Parallel Lines
c
d
/
"£
Exercises
1. Name each of the following.
a. four pairs of corresponding angles
b. three angles congruent to L 1
c. four angles supplementary to 4-1
2. Complete.
a. If L.1
=. ,then /II n.
b. If mL3 + m • = 180°, then /II n.
c. If L.2
then /II n.
=. ,
Find the measure of each numbered angle.
.., ~
a
~
L2
6. L4
8. L.6
3.L.1
5. L3
7. L.5
b
Find the measure of each numbered angle.
9.
10.
E
4l
12.
11.
Jm
2
I
'V
~
.._
'D
13. What must be the measure of each angle
in order that a II b?
a. L.1
b. L.2
c. L3
Name the segments or lines that must be parallel.
14.
~c
~d
15.
~a
~b
/
16.
E
A
B
C
7.3 Parallel Lines and Corresponding Angles
D
195
r--..._
Name the lines, if any, that must be parallel if each statement is true.
17. L1 := L4
18. L4 := L6
19. mL2 + mL1 = 180°
20. L8 := L9
21. L4 := L5
22. mL4 + mL8 = 180°
23. Draw a figure like the one shown.
a. Construct the line through P that is perpendicular to l.
b. Construct the line through P that is perpendicular to the
line constructed in part (a).
c. How is the line constructed in part (b) related to line l?
APPLICATIONS
24. Architecture In City Hall, Corridor One and Corridor Two are both
perpendicular to Corridor Three. Why can you say that Corridor One
and Corridor Two are parallel to each other?
25. Algebra Two parallel lines are cut by a transversal so that two
corresponding angles have measures (3x - 8) 0 and (2x + 10) 0 • Find
the value of x and the measures of the angles.
26. Computer The following LOGO program is for a turtle that likes to
travel backwards. Rewrite the program so it allows the user to decide
what the angles of the parallelogram will be.
To parallelogram
repeat 2 [bk 50 rt 40 rt 180 bk 20 rt 140 rt 180]
end
Test Yourself
Name each of the following.
1. two pairs of alternate interior angles
2. two pairs of same-side interior angles
3. four pairs of corresponding angles
4. all angles supplementary to L 1
5. all angles congruent to L 1
6. If mL2 = 60°, find the measures of L5, L6, and L7.
What must be the measure of each angle so that a II b?
7. L2
8. L3
9. L4
196
Chapter 7 Parallel Lines
p.
7.4
Constructing Parallel Lines
Objective: To construct the line parallel to a given line through a point not
on the line.
You can use the properties of angles formed by a transversal to construct
a line parallel to a given line.
- - - - - - - - · CONSTRUCTION 11 - - - - - - - - ·
Construct the line through P that
is parallel to line l.
p•
1. Draw a line l and a point P not on l.
Draw a line through P intersecting l.
2. _At vertex P, construct L.2 congruent to L.1.
Draw line m. Then m II l.
m
1. In Construction 11 , L.2 was constructed congruent to L.1. Why does
this guarantee that m II l ?
2. The figures show an alternative construction of line m parallel to the
given line l through the given point P.
a. Describe Step 1.
b. Describe Step 2.
m
c. Why is line m parallel to line l?
d. Why can this construction be considered
a special case of Construction 11?
7.4 Constructing Parallel Lines
197
Class Exercise
1. Draw a line m and a point A not on m. Construct the line through
A that is parallel to m.
Exercises
Using only the given information, can you conclude that a II b?
1.
~
2.
•
3.
a
b
b
4.
6.
5.
a
b
Draw a figure like the one shown. Construct the line through A that is
parallel to Bc.
7.
~
8.
C
B
9.
A
•A
c
A
B
•
c
10. Draw a line l. Construct two lines, one on each side of l, that are
parallel to l.
Draw a figure like the one shown. Construct the figure described.
11. rhombus JKLM with KL on line a
J
12. parallelogram ABCD
A
•
•
a
C
B
K
13. square EFGH with FG on line l
E•
14. trapezoid ABCD such that AD II BC and
AD= 2·BC
A•
B
198
Chapter 7 Parallel Lines
C
x
15. Draw a figure like the one shown and use it
to construct square WXYZ.
y
.4
P I•
I
I
I
16. Use the construction suggested by Postulate 10 on page 189
to construct the line through P that is parallel to l.
1
-;
APPLICATIONS
17. Space Geometry Given a point P not on line l, how many lines
through P do not intersect l?
18. Paper Folding Draw a line l and a point P not on l. Use paper folding
to determine the line through P that is parallel to l.
Thinking in Geometry
The following steps show an alternative construction of a line through
P parallel to l.
=
Step 1: From P, draw an
arc intersecting l at any
point A.
p
p
•
~
A<::::::::_
~
Step 3: Draw PC.
Step 2: Construct AB
PA
on l. With the same compass
setting and with the compass
point on P and then B, draw arcs
intersecting at some point C.
I
•
1. Why is h. PAC ::: h. BCA?
.
4. What kind of figure is PABC?
...
)B
AC:Z:::
•
'
P
/
/
/
/
//
• A<---
/
-----2
I
)B
AC:Z:::
~c
/
----
•
~
1---- --~"
/
"1c'\ ...
p
.
I
~
2. Why is L1 ::: L2?
3. Why is Pc Ill?
..
~
•
)II;
...
/
)/
//
I
~
•
w
5. Draw a figure like the one shown. Without copying
an angle, construct parallelogram WXYZ.
•
X
y
7.4 Constructing Parallel Lines
199
Thinking About Proof
Converses
On page 90 you learned that a conditional is a statement that can be written
in if-then form. When you interchange the hypothesis and conclusion of a
conditional statement, you get the converse of the original statement.
Example: Write the converse of each conditional.
a. If two parallel lines are cut by a transversal, then each
pair of alternate interior angles are congruent.
b. A rectangle is a parallelogram.
Solution: a. If two lines are cut by a transversal so that each pair of alternate
interior angles are congruent, then the lines are parallel.
b. Rewrite the conditional in if-then form:
If a figure is a rectangle, then it is a parallelogram.
Converse: If a figure is a parallelogram, then it is a
rectangle.
Part (b) of the Example demonstrates that the converse of a true conditional
does not have to be true. When a conditional and its converse are true, you
can combine them and write the combined statement in if-and-only-ifforrn:
Two lines cut by a transversal are parallel if and only if each pair of
alternate interior angles are congruent.
Exercises
Write the converse of each conditional.
1. If two angles of a triangle are congruent, then the sides opposite those
angles are congruent.
2. An equilateral triangle is also equiangular.
3. The three medians of a triangle are concurrent.
4. Vertical angles are congruent.
5. Which converses in Exercises 1-4 are true?
6. Combine Theorems 5.9 and 5.10 on page 138 in if-and-only-if form.
7. What is the converse of the converse of a conditional?
200
Chapter 7 Parallel Lines
7.5
Interior Angle Measures
of a Triangle
Objective: To use the sum of the interior angle measures of a triangle.
You know about the relationships among angles formed by parallel lines and a
transversal. Important relationships also exist among the angles of a triangle.
EXPLORING
r/; . . ,. . . ,. _
LJJ~~
1. Use the Geometric Supposer: Triangles disk to draw an acute triangle,
!:J.ABC. Through point C, draw DE so that it is parallel to side AB.
2. Sketch the figure. Use the Measure option to measure all the angles
formed. Record the measures on your sketch. What observations and
conjectures can you make about the angles of !:J.ABC? Repeat using a
right triangle, an isosceles triangle, and an equilateral triangle.
3. Explain why any of your conjectures must be true.
EXPLORING
Part A
1. Draw and cut out a scalene triangle. Fold the triangle as shown below
so that all three vertices meet on one side of the triangle.
/"\
/
//
/\
\
//
\.
/
/fti\
//
/_:~_
\
\
/
/
\
\
//
/~
\
\
~
2. What is the sum of the measures of the three angles of the triangle?
PartB
c
1. What is mL5 + mL3 + mL4?
l
2. Why is L5 =: Ll? Why is L4 =: L2?
3. What is mLl + mL3 + mL2?
A
.,L..__:__---i--~
7.5 Interior Angle Measures of a Triangle
201
The angles of a triangle are sometimes called the interior angles of the
triangle. The EXPLORING activities demonstrate the following theorem.
THEOREM 7.5 (Triangle Ang le-Sum Theorem): The sum of
the measures of the interior angles of any triangle is 180°.
EXPLORING
Part A
1. What kind of triangle is XYZ?
X
~z
2. What is mLX + mLY + mLZ? mLY? mLX + mLZ?
y
3. Describe the relationship of LX andLZ.
PartB
1. Draw an equilateral /:::,. RST and name the parts that are congruent.
2. What is the measure of each interior angle of /:::,. RST?
The Triangle Angle-Sum Theorem has the following corollaries.
COROLLARY 1 :
The acute angles of any right triangle are
complementary.
COROLLARY 2:
The measure of each interior angle of an
equilateral triangle is 60°.
Example: Find the measure of each numbered angle.
a. ~
60°
~2
Solution: a. mL1 + 75° + 60°
mL1 + 135°
mL1
mL1
mL2
mL2
202
Chapter 7 Parallel Lines
b.
M
~
•
= 180°
= 180°
= 180°
= 45°
= 180°
= 135°
b.
- 135°
- 45°
mL3
mL4 + 70° + 70°
mL4 + 140°
mL4
mL4
= 70°
= 180°
= 180°
= 180°
= 40°
-
140°
Thinking Critically
1. Is Part A of the second Exploring activity on page 201 an example of inductive
reasoning or deductive reasoning? Which type of reasoning is Part B?
2. Explain why the following statements are true.
a. A triangle must have at least one angle that measures at least 60°.
b. Every triangle must have at least two acute angles.
Class Exercises
n
Find the measure of each numbered angle.
1.
50°
4. 6
70°
3.
2.
[i
(1
1
5.
6.
Exercises
True or false? Give a reason or example to support each answer.
1. A triangle can have two 89° angles.
2. The acute angles of any right triangle are supplementary.
3. An equiangular triangle is a special kind of acute triangle.
4. A triangle can have angles of measure 74°, 43°, and 62°.
5. A right triangle can be equilateral.
6. An isosceles triangle can be obtuse.
7. A triangle can have no obtuse angles.
8. A triangle can have two right angles.
9. A right triangle can have an obtuse angle.
10. A triangle can have exactly one acute angle.
7.5 Interior Angle Measures of a Triangle
203
Find the measure of each numbered angle.
11.
il
12.
13.
15.6
16.
17.
18.
19.
20.
21.
22.
14.
~
..,1450 S 5 ( ) "
5
23. a. Ll
~
c
18"135"
b. LDAB
c. LDCB
d. L2
I
A
B
24. a. Ll
b. LPTR
c. L2
d. L3
Tv
~
•
25. One base angle of an isosceles triangle has a measure of 35°.
a. Find the measure of the other base angle.
b. Find the measure of the vertex angle.
26. The vertex angle of an isosceles triangle has a measure of 150°.
Find the measure of each base angle.
27. One acute angle of a right triangle has a measure of 28°.
Find the measure of the other acute angle.
28. fJ. PQR is isosceles. One of the base angles, LP, has a measure
- of 25°, and PQ
QR.
=
a. FindmLR.
204
b. FindmLQ.
Chapter 7 Parallel Lines
c. Classify fJ. PQR by its angles.
--
'R
29. a. Find mLl.
b. Find mL2.
c. Classify ~ABC by its sides.
Give a reason for your answer.
A.....___ _~~~
30. One angle of an obtuse isosceles triangle has a measure of 40°.
Find the measures of the other two angles.
31. To be Proven: If two angles of one triangle are congruent to
two angles of another triangle, then the third pair of angles
are congruent (Theorem 6.1).
Given: LA ::: LD; LB := LE
Prove: LC ::: LF
a. Since LA ::: LD and LB ::: LE,
b.
c.
d.
e.
F
A
~BD~E
.
mLA = • andmLB = • .
mLA + mLB = •
What are mLC and mLF? Why?
Substitute your answer from part (b) into one of your equations in
part (c). Is mLC = mLF?
Why is LC ::: LF?
APPLICATIONS
32. Algebra Two angles of a triangle are congruent. The third angle has
measure equal to the sum of the measures of the other two. Find the
measures of all three angles.
33. Algebra The measure of one acute angle of a right triangle is five
times the measure of the other acute angle. Find the measure of each
acute angle.
34. Algebra and Mental Math The measure of the largest angle of a
triangle is five times the measure of the smallest angle. The measure
of the third angle is three times the measure of the smallest angle.
Find the measures of all three angles.
Computer
Use the Your Own option on the Geometric Supposer: Triangles disk. Try to
make a triangle such that mLBA C = 120°, AB = 5, and mL CBA = 60°. What
happens? Explain.
7.5 Interior Angle Measures of a Triangle
205
7.6
Exterior Angle Measures
of a Triangle
Objective: To use the relationship between an exterior angle of a triangle
and its remote interior angles.
An exterior angle of a polygon is formed by one side of the
polygon and the extension of the adjacent side. For f:.ABC ,
L 1 is an exterior angle.
Every triangle has six exterior angles. The exterior angles of
f:. DEF are Ll , L2, L3, L4, L5, and L6. At each vertex,
the two exterior angles are congruent. Why?
Ll =: L2
L3 =: L4
L5 =: L6
Each exterior angle of a triangle has one adjacent interior
angle and two remote interior angles.
Example: For each exterior angle shown, name
one adjacent interior angle and two
remote interior angles.
Solution: Exterior angle
~---~
B
A
~~
.. -~~-..
,
D t6
2 ', E
~
~~
~--~
Adjacent interior angles
Remote interior angles
L7
L8
L8 , L9
Ll
L4
L7,L9
EXPLORING •
1. For each triangle, one exterior angle is shown. Find the measure of
each n~
umbered angle .
...,._4v 3 370
37°
.._ __2
A
~-·
2. Compare the measure of each exterior angle shown with the measure of
each of its remote interior angles. Are they the same? If not, which is greater?
3. Compare the measure of each exterior angle shown with the sum of the
measures of its remote interior angles. Are they the same?
206
Chapter 7
Parallel Lines
The EXPLORING activity demonstrates the following.
THEOREM 7.6: In a triangle, the measure of each exterior angle
is equal to the sum of the measures of its two remote interior angles.
COROLLARY: In a triangle, the measure of each exterior angle is
greater than the measure of either of its remote interior angles.
Thinking Critically
1. DoLl and L2 have the same adjacent interior angle
and remote interior angles?
2. Why is Ll ::: L2?
c
/ \ 1A~B
\
3. What is the relationship between an exterior angle of a
triangle and its adjacent interior angle?
'
4. Classify the exterior angles for an acute triangle,
a right triangle, and an obtuse triangle.
Class Exercises
1. Name the exterior angle adjacent to L2.
p~
2. Name the remote interior angles for L4.
3. Name an angle that is supplementary to L2.
4. mLl + mL3 = m •
5. mL4 = m •
Q
+ m•
Draw a triangle similar to, but larger than, each one shown. Then
draw and label an exterior angle at vertex A.
6.
FVA 1.v<Jz
A
8.
R
'-----~A
Find the measure of each numbered angle.
9.
50'l.d7
10. ~
~
11 . ....:--~
~
7.6 Exterior Angle Measures of a Triangle
207
Exercises
2
Name the adjacent interior angle and the two remote
interior angles for each exterior angle.
1. L 1
2. L2
3. L3
~
I
R~T-•
..lllfk-'".,.
S
3
Name each of the following.
4. three interior angles
5. six exterior angles
6. three angles that are neither exterior nor interior angles
7. the adjacent interior angle and two remote interior
angles for L4
8. two exterior angles for which L3 and L5 are the two
remote interior angles
9. six pairs of vertical angles
12
~~----------~
10
Draw a triangle similar to, but larger than, the one shown. Then draw
and label an exterior angle at vertex A.
~T
10.
S
11.
A
12.
A
B~C
X
A~G
Find the measure of each numbered angle.
13.
~
14.
~~ .
16.
A
15.
~
4\
17.
D
'
~~~
19.
20.
....__......
~
/
~
208
... 5
3\ 1
2' ....
~
Chapter 7 Parallel Lines
A
~--£_1
~
)1 8
18.
._h
150°
-~
'~ 11
True or false?
21. All exterior angles of an acute triangle are obtuse angles.
22. All exterior angles of an equiangular triangle are congruent.
23. All exterior angles of an obtuse triangle are acute angles.
X
24. All exterior angles of a right triangle are right angles.
Find the measure of each numbered angle.
25.
26.
48°
27.G 28.6
55°
97°
2
1
-
1__ ..,..
2
116°
--·
29. In 6 ABC, mLA = 45° and mLB = 80°. Find the measure of LC
and of an exterior angle at C.
30. In 6 PQR, mLP = 35° and the measure of an exterior angle at Q is
105°. Find the measures of LR and LQ.
-
-
31. Explain why AB and AC could not both
be perpendicular to BD.
•
A
~
..-.....
D
BC
APPLICATION
32. Calculator The measure of an exterior angle of a triangle is
twenty-three times the measure of its adjacent interior angle.
Find the measures of both angles.
Calculator
The measures of two angles of a triangle are 28° and 94 o. Andy and
Christine used different methods to find the measure of the third angle
with their calculators:
Andy's Method
28
180
1±1
E1
94
El
122
Christine's Method
122
El
180
E1
28
E1
94
El
58
58
Which method do you think was better? Give a reason for your answer.
7.6 Exterior Angle Measures of a Triangle
209
7.7 Angle Measures of a PolygQn
Objective: To find the sum of angle measures of any polygon.
You can use the sum of the interior angle measures of a triangle to
determine angle measures in other polygons.
EXPLORING
1. Draw a quadrilateral like the one shown. Use a protractor to measure
LQ, LQUA, LA, and LADQ. Use a calculator to find the sum.
2. Use the Triangle Angle-Sum Theorem to find the sum of the measures
of the interior angles of DQUA. Compare your results with Step 1.
The EXPLORING activity demonstrates the following theorem.
THEOREM 7. 7: The sum of the measures of the interior angles of
any quadrilateral is 360°.
To find the sum of the measures of the interior angles of any polygon, draw
all possible diagonals from one vertex. Then find the sum of the measures
of the interior angles of the triangles formed.
Triangles I Sum of Interior
Formed Angle Measures
Polygon
Sides
Pentagon
5
~
~
3
3 X 180° = 540°
Hexagon
6
8
4
4
Figure
-
''
X
180°
= 720°
-
These results and the EXPLORING activity suggest the following theorem.
THEOREM 7.8 (Interior Angle Sum Theorem): The sum of the
measures of the interior angles of a polygon with n sides is (n - 2)180°.
210
Chapter 7
Parallel Lines
hA
QU/
D
Example 1: Find mLl.
~
Solution: mL1 + 98° + 115° + 90° + 121 o = (5-2) 180°
mL1 + 424° = 540°
mL1 = 540° - 424°
= 116°
EXPLORING
1. What is mL 1 + mL2? What is the sum of the measures of
each exterior angle and adjacent interior angle?
2. What is the sum of the measures of all the numbered angles
shown?
3. What is the sum of the measures of the interior angles?
4. Subtract the sum of the measures of the interior angles
(Step 3) from the sum in Step 2 to find the sum of the
measures of the exterior angles, one at each vertex.
.lllllt:' ........ D
5. Draw a triangle or quadrilateral. Draw one exterior angle at
each vertex. Number these exterior angles and the interior
angles. Repeat Steps 1-4 for your figure .
This EXPLORING activity demonstrates the following theorem.
THEOREM 7.9 (Exterior Angle Sum Theorem): The sum
of the measures of the exterior angles, one at each vertex, of any
polygon is 360°.
Example 2: The measure of each exterior angle of a regular polygon
is 18°. Find the number of sides.
Solution: Let n = the number of sides.
18° • n = 360°
n = 20
There are 20 sides.
7.7 Angle Measures of a Polygon
211
1. Why are the exterior angles of a regular polygon congruent?
2. For what kind of polygon does the sum of the interior angles equal the
sum of the exterior angles, one exterior angle at each vertex?
~
Class Exercises
Find the sum of the measures of the interior angles of a polygon with
the given number of sides.
1. 7 sides
2. 9 sides
3. 10 sides
4. The measure of each interior angle of a regular polygon is 135°.
a. Find the measure of each exterior angle.
b. Find the number of sides.
Find the measure of each numbered angle.
5. ~
7.
6.
~-~
Exercises
Copy and complete the table.
Sum of the Interior
Angle Measures
Number of Sides
of Polygon
Sum of the Exterior
Angle Measures
i
1.
2.
3.
4.
5.
•
••
4
360°
••
••
4 • 180 = 720°
6
•
7 • 180 = 1,260°
16
24
7. 0 :r
!
!
I
.i
Find the measure of each numbered angle.
6.
8.
/\
.,._
..,
50° 4
90°
212
105°1
Chapter 7
2
10oo ~.....
Parallel Lines
Jl-
16
~
9. regular pentagon
3\
2
~
\ 110"
....
€J
2
_,...
Copy and complete the table .
. . - Number of Sides of
Regular Polygon
10.
5
11.
9
M easure of Each
Inter ior Angle
Measure of Each
Exterior Angle
•
•
••
••
•
12.
13.
14.
D
Gl
n
90
144°
160°
I
The sum of the measures of the interior angles is given for some
polygons. Find the number of sides of each polygon.
15. 540°
16. 900°
17. 1,440°
18. 1,800°
19. 2,340°
20. 3,240°
Draw and label a figure for each polygon described, if possible. If it is
not possible, explain why.
21. triangle: exterior angles-obtuse angles
22. triangle: exterior angles-2 right angles, 4 obtuse angles
23. quadrilateral: exterior angles---4 obtuse angles, 4 acute angles
24. quadrilateral: interior angles- 4 acute angles
25. quadrilateral: interior angles-2 obtuse angles, 1 right angle, 1 acute angle
26. pentagon: interior angles- 5 acute angles
APPLICATION
27. Sports Research the shape of the home plate used in baseball. Sketch
home plate and give the measures of its interior angles.
Everyday Geometry
Bees construct honeycombs in the shape of
regular hexagons. Do library research to
find out what advantages this structure
offers the bees.
7.7 Angle Measures of a Polygon
213
7.8
Problem Solving Application:
Interpreting Contour Maps
Objective: To solve problems involving contour maps.
If a plane intersects a portion of Earth's surface, the intersection is a closed
curve. In the figure below, parallel planes Land M intersect the mountain at
elevations of 7,000 ft and 8,000 ft respectively. The resulting contour lines
show the shape of the mountain at the two elevations.
A map depicting Earth's surface at different cross sections is a contour map.
The closer the lines are to each other, the steeper the terrain. Hikers,
mountain climbers, and highway engineers use contour maps to plan routes
between places.
=>
contour map
Example: Find the elevations of points A, B, and Con the
contour map.
contour
interval:
200ft
Solution: Point A lies on the 4,400-ft contour line, so its
elevation is exactly 4,400 ft. Point B lies between
4,200 ft and 4,400 ft. Point C lies inside the 4,600-ft
curve, so its elevation is greater than 4,600 ft but
less than 4,800 ft.
214
Chapter 7
Parallel Lines
Class Exercises
Use the contour map shown on this
page to answer these questions.
1. What is the difference in elevation
between adjacent contour lines?
2. What is the elevation of Bascom
Lodge?
3. Describe the difference in elevation
between Wilbur Clearing Lean-to
and Bascom Lodge. If you cannot
write an exact elevation, give a
range.
Exercises
Use the contour map shown on this
page to answer these questions.
1. State the elevations of the Money
Brook Lean-to and the intersection
of the Hopper and Overlook Trails.
If you cannot write an exact
elevation, give a range.
2. Suppose you hiked along the trail
from the Mt. Williams campsite to
Bascom Lodge. What is the change
in elevation?
3. What is the elevation of the highest
point on Mt. Prospect Trail?
4. Explain why roads and hiking trails
do not usually proceed in a straight
line, but curve and loop as you
travel between places.
- - Trail
1::t Lean-to/Lodge
Elevation is given in feet.
LEGEND
.A. Campsite
Road
Draw sketches of contour maps showing the following types of terrain.
5. a steep mountainside
6. a gentle sloping hillside
7.8 Problem Solving Application: Interpreting Contour Maps
215
Chapter 7 Review
Vocabulary
You should be able to write a brief description, draw a picture, or give an
example to illustrate the meaning of each of the following terms.
Vocabulary
converse (p. 200)
corollary (p. 194)
transversal (p. 185)
Angles determined by a transversal
alternate interior angles (p. 185)
corresponding angles (p. 185)
exterior angles (p. 185)
interior angles (p.185)
same-side exterior angles (p. 186)
same-side interior angles (p. 186)
Angles of a triangle
adjacent interior angle (p. 206)
exterior angle (p. 206)
interior angles (p. 202)
remote interior angles (p. 206)
Summary
The following list indicates the major skills, facts, and results you should
have mastered in this chapter.
7. 1 Identify the interior, exterior, alternate interior, corresponding, and
same-side interior and exterior angles formed when two lines are cut
by a transversal. (pp. 185-187)
7.2 Use facts about the interior angles formed when two parallel lines are
cut by a transversal and use relationships between interior angles to
determine when two lines are parallel. (pp. 188-192)
7.3 Use facts about parallel lines cut by a transversal and pairs of
corresponding angles. (pp. 193-196)
7.4 Construct the line parallel to a given line through a point not on the
line. (pp. 197-199)
7. 5 Use the fact that the sum of the interior angle measures of a triangle
is 180°. (pp. 201-205)
7.6 Use the relationship between an exterior angle of a triangle and its
remote interior angles. (pp. 206-209)
7.7 Find the sum of angle measures of any polygon. (pp. 210-213)
7.8 Solve problems involving contour maps. (pp. 214-215)
216
Chapter 7 Review
Exercises
Describe the angle or pair of angles. Use interior, exterior, alternate
interior, corresponding, same-side interior, or same-side exterior.
2. L5
5. L4 and L5
8. L2 and L6
1. L7
4. L2 and L8
7. L1 and L5
3. L4
6. L6 and L4
9. L1 and L7
j
~
3
L/1..
ABCD is a parallelogram. Classify each statement as true or false. A
10. L2 ::: L5
11. mL3 + mL4 = 180°
12. mL? + mL8 = 180°
14. L7 ::: L4
13. mL3 + mL6 = 180°
15. mLABC + mL4 = 180°
16. L1 ::: L7
17. LADC ::: L8
B
1
2
6 5
3
7
•
4 8
D
C
Name the lines, if any, that must be parallel if each
statement is true.
b
18. L1 ::: L6
19. L1 ::: L2
c
20. L1 ::: L5
21. L2 ::: L4
22. mL3 + mL5 = 180°
23. L4::: L6
d
24. Draw an acute triangle ABC. Construct a line parallel to BC through
A and a line parallel to AB through C.
Find the measure of each numbered angle.
· 25. - ~
85°
1
35°
26. ~1
~
~
27.
~---~\____A
28. Find the sum of the measures of the interior angles of a 30-sided polygon.
29. The sum of the measures of the interior angles of a polygon is 2,160°.
Find the number of sides.
PROBLEM SOLVING
contour
30. Estimate the difference in elevation between
interval:
points A and B.
' - - - - - - - - - - - - ' 50.ft
Chapter 7 Review
217
··'? Chapi~~~1Z2Je~t
'
,,·~;·
i
,_._·::/fV:.-)7-;,c~~:(~JJti:,;;,:;::;.'~i ' __ :·.r:~,
:,:·," :•.. '- -:•:,_;:, -:,:/, .:~- -:.: -
~"'
1. Name the transversal.
2. Name three exterior angles and three interior angles.
3. N arne one pair of same-side interior angles and one pair
of same-side exterior angles.
4. N arne one pair of alternate interior angles.
5. N arne two pairs of corresponding angles.
Find the measure of each angle. Assume that a II b, c II d, and e llf.
6. Ll
7. L3
8. L6
1c
Name the lines, if any, that must be parallel if
each statement is true.
9. L5 := L6
10. Ll := L4
11. L3 := L7
12. mL8 = 95°
13. mL2 = 45°
14. mL3 = 45°
'!
a
15. Draw a line k and a point P not on k. Choose any point Q on k and
construct rhombus PQRS with QR on k.
Complete.
16. In h. ABC, if mLA = 54° and mLB = 71°, then mLC = • .
17. The sum of the measures of the interior angles of a polygon is 6,840°.
The polygon has • sides.
18. The sum of the measures of the interior angles of a 36-sided polygon
is • . The sum of the measures of the exterior angles is • .
Find the measure of each numbered angle.
19. ~
78°
56°
20.
.
---·
1
21. ~
~
PROBLEM SOLVING
22. State the elevations of points A, B, C, and D.
If you cannot write an exact elevation, give
a range.
218
Chapter 7 Test
contour
interval:
100ft