Download Cosmic Microwave Background Anisotropies:

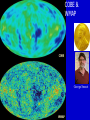
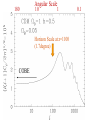
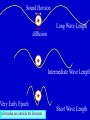
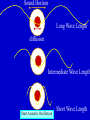
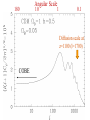
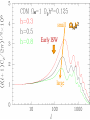
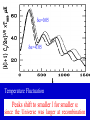
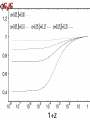
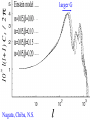
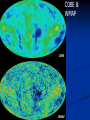
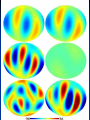
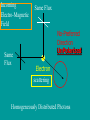
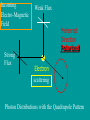
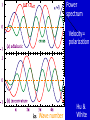
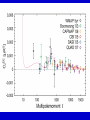
Cosmic Microwave Background
Basic Physical Process:
Why so Important for Cosmology
Naoshi Sugiyama
Department of Physics, Nagoya University
Institute for Physics and Mathematics of the Universe, Univ.
Tokyo
Before Start!
GCOE @ Nagoya U.
• We have a program of Japanese government, Global
Center of Excellence Program (GCOE). This Global COE
recruits graduate students. For those who are interested in
doing their PhD work on particle physics, cosmology,
astrophysics, please contact me! We are also planning to
have a winter school in Feb. for dark matter and dark
energy.
If you are interested, please contact me:
[email protected]
or visit
http://www.gcoe.phys.nagoya-u.ac.jp/
Institute for Physics and
Mathematics of the Universe
• IPMU is a new truly international institute
established in 2008.
• There are a number of post doc positions available
every year.
• We are hiring faculties too.
• At least 30% of members have to be non-Japanese.
• Official language of this institute is English.
Basic Equations and Notations
• Friedmann Equation
r K
 a 

2  m
H     H 0  3  4  2   
a
a
a
a

2
2
H 0 : Hubble, a : scale factor, 0 denotes present
a0  1
 m : matter,  r : radiation,  K : curvature
  : dark energy
• redshift
1  z  a0 / a  1 / a
Basic Equations and Notations
• Metric: Friedmann-Robertson-Walker
2

dr
2
2
2
2
2
ds  cdt  a 
 r d 
2
 1  Kr

• Horizon Scale
(a)  a(t )  dt / a(t )  c / H (a)
dH
Physical
dH
comoving
 (a0 / a)d H
Physical
§1. Introduction
• What’s Cosmic Microwave Background
radiation?
 Directly Brings Information at t=380,000, T=3000K
Fossil of the early Universe
 Almost perfect Black Body
Evidence of Big Bang
-5
 Very Isotropic: T/T  10
Evidence of the Friedmann Universe
 Information beyond Horizon
Evidence of Inflation
What happened at t=380,000yr
• Recombination: almost of all free electrons were
captured by protons, and formed hydrogen atoms
• Hereafter, photons could be freely traveled.
Before recombination, photons frequently
scattered off electrons.
The universe became transparent!
3min
Temperature 1GK
Multiple
Scattering
380Kyr.
transparent
１３.７Gyr.
Photon transfer
Recombi
nation
Nucleo Synthesis
Big Bang
photon
helium
Time
3000Ｋ
Big Bang
Hydrogen atom
2.725K
Cosmic Microwave Background
• If the Universe was in the thermal equilibrium,
photon distribution must be Planck distribution
(Black Body)
• Energy Density of Photons is
(1  z ) 4
Why Information beyond Horizon?
Horizon Size at recombination
• Here we assume matter dominant, a is the scale
factor, H is the Hubble parameter.
Horizon Size at present
• Using the same formula in the previous page, but
insert z=0, instead z=1100. Here we ignore a dark
energy contribution in the Hubble parameter
d H (t0 )  180( M h 2 ) 1/ 2 (1100)1/ 2 Mpc
2 1/ 2
 6000( M h )
Mpc
Angular Size of the Horizon at z=1100
• Angular size of the Horizon at z=1100 on the Sky
can be written as
c
  d H (trec ) / d H (t0 )  0.030rad  1.7degree
C.f. angular size of the moon is 0.5 degree
1.7degree
dHc(z=1100)
dH(z=0)
There must not have any causal contact beyond Horizon
Same CMB temperature
Univ. should expand faster than speed of light
Horizon Problem
Inflation
§2. Anisotropies
• As a first approximation, CMB is almost perfect
Black Body, and same temperature in any direction
(Isotropic)
• It turns out, deviation from isotropy, i.e.,
anisotropy contains rich information
• Two anisotropies
– Spectral Distortion
– Spatial Anisotropy
2-1. Spectral Distortion
Extremely Good Black Body Shape in average
Observation by COBE/FIRAS
y-distortion
y < 1.5x10-5 y   dlne T
-distortion || < 9x10-5
8h
f  3
c
3
 h
kTe
me c 2

exp 
   1
 kT

Sunyaev-Zeldovich Effect
y-distortion
• Caused by: Thermal electrons scatter off photons
• Photon distribution function: move low energy
photons to higher energy
Distribution function
lower
higher • distort Black Body
low freq: lower temp
high freq: higher temp
no change: 220GHz
frequency
SZ Effect
f: photon distribution function
Energy Transfer: Kompaneets Equation
y-parameter:
k: Boltzmann Const, Te: electron temperature, me: electron
mass, ne: electron number density, T: Thomson Scattering
Cross-section , : Optication depth
Solution of the equation
fPL: Planck distribution
low freq. limit: x<<1 f / f  2 y decrement
high freq. limit: x>>1 f / f  yx 2 increment
f/f=T/T in low frequency limit (depend on the
definition of the temperature)
• SZ Effect Provides Information of
– Thermal History of the Universe
– Thermal Plasma in the cluster of galaxies
Hot
ionized
gas in a
cluster of
galaxies
CMB
Photon
Q: typically, gas within a big cluster of galaxies is 100 million
K, and optical depth is 0.01. What are the values of y and
temperature fluctuations (low frequency) we expect to have?
http://astro.uchicago.edu/sza/overview.html
•Clusters provide SZ signal.
•However, in total, the Universe is filled by CMB
with almost perfect Planck distribution
wavelength[mm]
intensity[MJy/str]
COBE/FIRAS
200 sigma
error-bars
2.725K Planck
distribution
frequency[GHz]
Cosmic Microwave Background
• Direct Evidence of Big Bang
– Found in 1964 by Penzias & Wilson
– Very Precise Black Body by COBE in 1989 (J.Mather)
John Mather
Arno Allan
Penzias
Robert
Woodrow
Wilson
2-2. Spatial Anisotropies
 1976: Dipole Anisotropy was discovered
3mK  peculiar motion of the Solar System
to the CMB rest frame
Annual motion of the earth is detected by COBE:
the Final proof of heliocentrism
Primordial Temperature Fluctuations
of Cosmic Microwave Background
• Found by COBE/DMR in 1992 (G.Smoot),
measured in detail by WMAP in 2003
• Structure at 380,000 yrs (z=1100)
– Recombination epoch of Hydrogen atoms
• Missing Link between Inflation (10-36s) and
Present (13.7 Billion yrs)
• Ideal Probe of Cosmological Parameters
– Typical Sizes of Fluctuation Patters are
Theoretically Known as Functions of Various
Cosmological Parameters
COBE 4yr data
COBE &
WMAP
George Smoot
Temperature Anisotropies:
Origin and Evolution
Origin: Hector de Vega’s Lecture
• Quantum Fluctuations during the Inflation Era
10-36[s]
• 0-point vibrations of the vacuum generate
inhomogeneity of the expansion rate, H
• Inhomogeneity of H translates into density
fluctuations
Temperature Anisotropies:
Origin and Evolution
Evolution
• Density fluctuations within photon-proton-electron
plasma, in the expanding Universe
• Dark matters control gravity
 Photon:
Distribution function  Boltzmann Equation
 Proton-Electron
Fluid coupled with photons through Thomson Scattering 
Euler Equation
 Dark
Matter
Fluid coupled with others only through gravity  Euler Eq.
C
Boltzmann Equation
C: Scattering Term
Perturbed FRW Space-Time
Temperature Fluctuations
Optical Depth
Anisotropic Stress
Fluid Components:
Proton-electron
dm
dm
dm
dm
Dark Matter
Numerically Solve Photon, Proton-Electron and
dark matter System in the Expanding Universe
Boltzmann Code, e.g., CMBFAST, CAMB
Fluctuations
Long Wave Mode
Scale Factor
Fluctuations
Short Wave Mode
Scale Factor
§3. What can we learn from spatial
anisotropies?
Observables
1. Angular Power spectrum
– If fluctuations are Gaussian, Power spectrum (r.m.s.)
contain all information
2. Phase Information
– Non-Gaussianity
– Global Topology of the Universe
3. Polarization
– Tensor (gravitational wave) mode
– Reionization (first star formation)
3-1. Angular Power Spectrum
• Cl
T/T(x)
Angular Power Spectrum
• <|T/T(x)|2>=(2l+1)Cl/4dl (2l+1)Cl/4
= (dl/l) l(2l+1)Cl/4
• Therefore, logarithmic interval of the temperature
power in l is l(2l+1)Cl/4 or often uses
l(l+1)Cl/2
• l corresponds to the angular size 
l=/=180[(1 degree)/]
C.f. COBE’s angular resolution is 7 degree, l<16
Horizon Size (1.7 degree) corresponds to l=110
180
Angular Scale
10
1
Horizon Scale at z=1100
(1.7degree)
COBE
0.1
3-2. Physical Process
Different Physical Processes had been working
on different scales
• Gravitational Redshift on Large Scale
– Sachs-Wolfe Effect
• Acoustic Oscillations on Intermediate Scale
– Acoustic Peaks
• Diffusion Damping on Small Scale
– Silk Damping
Individual Process
(a) Gravitational Redshift: large scales
What is the gravitational
redshift?
• Photon loses its energy when it climbs up the
potential well: becomes redder
• Photon gets energy when it goes down the potential
well : becomes bluer
h
h-mgh= h-(h /c2)gh
= h(1-gh/c2)
 h’
h
Surface of the earth
Individual Process
(a) Gravitational Redshift: large scales
1)Lose energy when escape from gravitational potential
: Sachs-Wolfe
redshift

grav. potential at Last Scattering Surface
2)Get (lose) energy when grav. potential decays (grows)
: Integrated Sachs-Wolfe, Rees-Sciama
E=|1-2|
1
2
blue-shift
Comments on Integrated Sachs-Wolfe Effect (ISW)
• If the Universe is flat without dark energy
(Einstein-de Sitter Univ.), potential stays constant
for linear fluctuations: No ISW effect
ISW probes curvature / dark energy
•Curvature or dark energy can be only important in
very late time for evolution of the Universe
Since late time=larger horizon size, ISW
affects Cl on very small l’s
Late ISW
•However, when the universe became matter
domination from radiation domination, potential
decayed! This epoch is near recombination
contribution on l ~ 100-200 Early ISW
Early ISW (low matter
density)
Late ISW(dark energy/curv)
No ISW, pure SW for flat no dark energy
(b) Acoustic Oscillation: intermediate scales
 scales smaller than sound horizon
Harmonic oscillation in gravitaional Potential
Why Acoustic Oscillation?
• Before Recombination, the Universe contained
electrons, protons and photons (plasma) which are
compressive fluid.
• The density fluctuations of compressive fluid are
sound wave, i.e., Acoustic Oscillation.
Before Recombination, the Universe was filled be
a sound of ionized.
Cosmic Symphony
(b) Acoustic Oscillation: intermediate scales
 scales smaller than sound horizon
Harmonic oscil. in grav. potential
2
analogy balls & springs in the well: balls’mass Bh
1) set at initial location = initial cond.
hold them until sound horizon cross
2) oscillate after sound horizon crossing
3) at Last Scatt. Surface (LSS), climb up potential well
 long wave length > sound horizon
stay at initial location until LSS  Pure Sachs-Wolfe
 First Compress.(depress.) at LSSfirst (second) peak
Sound Horizon
Long Wave Length
diffusion
Intermediate Wave Length
Very Early Epoch
All modes are outside the Horizon
Short Wave Length
Sound Horizon
Long Wave Length
diffusion
Intermediate Wave Length
Start Acoustic Oscillation
Short Wave Length
Long Wave Length
Start Acoustic Oscillation
Intermediate Wave Length
Diffusion Damping: Erase!
Short Wave Length
Conserve Initial
Fluctuations
Acoustic Oscillation
Long Wave Length
Intermediate Wave Length
Recombination
Short Wave Length
Diffusion Damping: Erase!
Epoch
Peak Locations
-Projection of Sound Horizon• Sound Horizon: dsc (z=1100)= (cs/c)dHc (z=1100)
• Distance: Horizon Scale dH
ds
dH
Sound velocity at recombination
• baryon density
b=(1+z)3Bc=1.88h210-29(1+z)3B g/cm3
• Photon density
=4.6310-34(1+z)4g/cm3
Sound Horizon Size at recombination
• Here we take Bh2=0.02
Question: Calculate angular size of the sound horizon
at recombination, and corresponding l.
180
Angular Scale
10
1
0.1
Sound Horizon z=1100 higher
harmonics
COBE
Solution of the Boltzmann equation
 k (t )  A sin( cs k Physicalt )  B cos(cs k Physicalt )
 A sin( cs k )  B cos(cs k )
   dt / a(t )  d
comoving
H
cs k  1
k (cs / c ) d
comoving
Sound
kd
comoving
H
1
1
/c
(c) Diffusion damping: small scales
(Silk Damping)
caused by photon’s random walk
Number of photon scattering per unit time
Mean Free Path
N is the number of scattering during cosmic time.
Cosmic time is 2/H for matter dominated universe
Diffusion of random walk
Comoving diffusion scale (physical(1+z))
At recombination
The corresponding angular scale and l are
ld  180(1degree/  )  1700
2
2

h

0
.
02
,

h
 0.15
Here, assume B
M
180
Angular Scale
10
1
0.1
Diffusion scale at
z=1100 (l=1700)
COBE
Acoustic Oscillations
Late ISW for dark energy
COBE
Gravitaional Redshift
(Sachs-Wolfe)
Large
10°
Early ISW
Diffusion
damping
1°
10mi Small
3-3. What control Angular Spectrum
• Initial Condition of Fluctuations
– If Power law, its index n (P(k)kn)
– Adiabatic vs Isocurvature
• Sound Velocity at Recombination
– Baryon Density: Bh2
• Radiation component at recombination
modifies Horizon Size and generates early ISW
– Matter Density: Mh2
• Radiative Transfer between Recombination and
Present
– Space Curvature: K
3-3. What control Angular Spectrum
• Initial Condition of Fluctuations
– If Power law, its index n (P(k)kn)
– Adiabatic vs Isocurvature
• Sound Velocity at Recombination
– Baryon Density: Bh2
• Radiation component at recombination
modifies Horizon Size and generates early ISW
– Matter Density: Mh2
• Radiative Transfer between Recombination and
Present
– Space Curvature: K
Initial Condition
Adiabatic vs Isocurvature
• Adiabatic corresponds to
T/T(k, )=Bcos (kcs)
• Isocurvature corresponds to
T/T(k, )=Asin(kcs)
3-3. What control Angular Spectrum
• Initial Condition of Fluctuations
– If Power law, its index n (P(k)kn)
– Adiabatic vs Isocurvature
• Sound Velocity at Recombination
– Baryon Density: Bh2
• Radiation component at recombination
modifies Horizon Size and generates early ISW
– Matter Density: Mh2
• Radiative Transfer between Recombination and
Present
– Space Curvature: K
Sound velocity at recombination
• If Cs becomes smaller, i.e., bBh2 becomes
larger, balls are heavier (or spring becomes weaker)
in our analogy of acoustic oscillation.
• Heavier balls lead to larger oscillation amplitude
for compressive modes (but not rarefaction modes).
M
large
Bh2
large
small
small
3-3. What control Angular Spectrum
• Initial Condition of Fluctuations
– If Power law, its index n (P(k)kn)
– Adiabatic vs Isocurvature
• Sound Velocity at Recombination
– Baryon Density: Bh2
• Radiation component at recombination
modifies Horizon Size and generates early ISW
– Matter Density: Mh2
• Radiative Transfer between Recombination and
Present
– Space Curvature: K
Horizon Size at recombination
• Here we assume matter dominant.
In reality, H 2  H 2   M   R 
0
 a 3
a 4 
Larger Rh2 or smaller Bh2 makes the horizon size
smaller
Shift the peak to smaller scale i.e., larger l
Early ISW effect
• Larger Rh2 or smaller Bh2 shifts the matter
domination to the later epoch
• Early ISW: decay of gravitational potential when
matter and radiation densities are equal
More Early ISW on larger scale i.e., smaller l
M
small Mh2
Early ISW
large
3-3. What control Angular Spectrum
• Initial Condition of Fluctuations
– If Power law, its index n (P(k)kn)
– Adiabatic vs Isocurvature
• Sound Velocity at Recombination
– Baryon Density: Bh2
• Radiation component at recombination
modifies Horizon Size and generates early ISW
– Matter Density: Mh2
• Radiative Transfer between Recombination and
Present
– Space Curvature: K
Radiative Transfer:
depend on the curvature
Flat
Observer
Horizon Distance
Observe Apparent Size
Space Curvature=Lens
Radiative Transfer:
depend on the curvature
Flat, 0 Curvature
Observer
Space Curvature=Lens
Radiative Transfer:
depend on the curvature
Positive Curvature
Observer
Magnify!
Space Curvature=Lens
Radiative Transfer:
depend on the curvature
Negative Curvature
Observer
Shrink!
Projection from LSS to l
[i] flat =1
[ii]  & <1: Further LSS
[iii] open <1: Geodesic effect
large l
large l


smaller 
pushes peaks to
smaller 
pushes peakes to
More Negatively
Curved
Optical Depth 
• After recombination, the universe is really
transparent?
• Answer: NO!
It is known z<6, the inter-galactic gases are
ionized from observations  Free Electrons
• Stars and AGN (quasars) produced ionized
photons, E>13.6eV
The Universe gets partially Clouded!
Define Optical Depth of Thomson Scattering as
   dtne T
Temperature Fluctuations are Damped as
T / T  T / TNoDamping  e

 can be a probe of the epoch of reionization
(first star formation).
(Polarization is very important clue for reionization)
Recombination
400,000yr
Big Bang
13.7Byr.
Ionized
gas
Scattering at recombination
Big Bang
Recombination
Ionized Gas
Ionized
gas
Star Formation
Some photons last scattered at the late epoch
Temperature Fluctuations Damped away on the
scale smaller than the horizon at reionizatoion
N.S., Silk, Vittorio, ApJL (1993), 419, L1
What else can CMB anisotropies be
sensitive?
For Example
• Number of Neutrino Species (light particle species)
• Time Variation of Fundamental Constants such as
G, c,  (Fine Structure Constant)
Number of Massless Neutrino Family
If neutrino masses < 0.1eV,
neutrinos are massless until the recombination epoch
Let us increase the number of massless species
Shifts the matter-radiation equality epoch later
More Early Integrated ISW
• Peak heights become higher
• Peak locations shift to smaller scales, i.e., larger l
Measure the family
number at z=1000
Time Variation of Fundamental Constants
Varying  and CMB anisotropies
Battye et al. PRD 63 (2001) 043505
QSO absorption lines:
  [(t20bilion yr)- (t0)]/ (t0) = -0.72±0.1810-5
QSO absorption line
 = -0.72±0.1810-5
0.5 < z < 3.5
Webb et al.
Influence on CMB
Thomson Scattering:
d/dtxeneT
: optical depth, xe: ionization fraction
ne: total electron density, T: cross section
If  is changed
1) T2 is changed
2) Temperature dependence of xe i.e., temperature
dependence of recombination preocess is modified
For example, 13.6eV = 2mec2/2 is changed!
If  was smaller, recombination became later
If =±5%, z~100
Flat, M=0.3, h=0.65, Bh2=0.019
Ionization fraction
=-0.05
=0.05
=0.05
=-0.05
Temperature Fluctuation
Peaks shift to smaller l for smaller 
since the Universe was larger at recombination
Varying G and CMB anisotropies
• Brans-Dicke / Scalar-Tensor Theory
G  1/ (scalar filed)
: G may be smaller in the early epoch
• Stringent Constraint from Solar-system
: must be very close to General Relativity
BUT, it’s not necessarily the case
in the early universe
G0/G
If G was larger in the early universe,
the horizon scale became smaller
c/H = c(3/8G)
Peaks shift to larger l
larger G
Nagata, Chiba, N.S.
We have hope to determine
cosmological parameters together with
the values of fundamental quantities,
i.e., , G
and the nature of elementary particles
at the recombination epoch
by measuring CMB anisotropies
Angular Power Spectrum is
sensitive to
• Values of the Cosmological Parameters
–
–
–
–
–
M h 2
 Bh2
h
Curvature K
Initial Power Spectral Index n
• Amount of massless and massive particles
• Fundamental Physical Parameters
Bayesian analysis
Markov chain Monte Carlo (MCMC)
Comparison with Observations and set constraints
Question
• increase Bh2  higher peak, decrease Mh2 
higher peak. How do you distinguish these two
effects?
For that, calculate l(l+1)Cl /2 for Bh2=0.02 and
Mh2 =0.15 (fiducial model). Then increase Bh2
to 0.03, and find the value of Mh2 which provides
the same first peak height as the fiducial model.
And compare the resultant l(l+1)Cl /2 with the
fiducial model.
h=0.7, n=1. flat, no dark energy
3-4. Beyond Power Spectrum:
Phase
• Gaussian v.s. Non-Gaussian
– If Gaussian, angular power spectrum contains all
information
– Inflation generally predicts only small non-Gaussianity
due to the second order effect
• Rare Cold or Hot Spot?
• Global Topology of the Universe
Non-Gaussianity

Fluctuations generated during the inflation
epoch
Quantum Origin
 Gaussian as a first approximation
(x)((x)-)/

0 (x)
How to quantify non-Gaussianity
• In real space
– Skewness
– Kurtosis
How to quantify non-Gaussianity
• In Fourier Space
– Bispectrum
Fourier Transfer of 3 point
correlation function
In case of the temperature angular spectrum,
Wigner 3-j symbol
– Trispectrum
Bispectrum
• If Gaussian, Bispectrum must be zero
• Depending upon the shape of the triangle, it
describes different nature
– Local
– Equilateral
Global Topology of the Universe
Three torus universe
Circle in the sky
CMB sky in a flat three torus universe
Cornish & Spergel PRD62 (2000)087304
Angular Power Spectrum is
sensitive to
• Values of the Cosmological Parameters
–
–
–
–
–
M h 2
 Bh2
h
Curvature K
Initial Power Spectral Index n
ONE NOTE!
• Amount of massless and massive particles
• Fundamental Physical Parameters
Bayesian analysis
Markov chain Monte Carlo (MCMC)
Comparison with Observations and set constraints
Geometrical Degeneracy
Efstathiou and Bond
baryon and CDM density: Bh , Mh
 Identical primordial
Degenerate contour
fluctuation spectra
m= 1- K- 
 Identical Angular
Diameter R(, K)
=0
2
 Identical
Should Give Identical
Power Spectrum
close to the flat geometry
BUT not quite!
flat
2
Projection from LSS to l
[i] flat =1
[ii]  & <1: Further LSS
[iii] open <1: Geodesic effect
large l
large l


smaller 
pushes peaks to
smaller 
pushes peakes to
Almost degenerate models
For same value
of R
Degenerate
line
h=0.5
What we can determine from CMB power spectrum is
Bh2, mh2,
degenerate line (nearly curvature)
Difficult to measure
curvature itself and  , m, B directly
Question: Generate Cl’s on this degenerate line for
M=0.3, 0.5, 0.6 and make sure they are degenerate.
§3. Observations and Constraints

COBE
Clearly see large scale (low l ) tail
 angular resolution was too bad to resolve peaks


Balloon borne/Grand Base experiments
Boomerang, MAXMA, CBI, Saskatoon, Python,
OVRO, etc
 See some evidence of the first peak, even in Last
Century!


WMAP
CMB observations
by 1999
COBE &
WMAP
WMAP
Observation
1st yr
3 yr
WMAP Temperature Power Spectrum
• Clear existence of large scale Plateau
• Clear existence of Acoustic Peaks (up to 2nd or 3rd )
• 3rd Peak has been seen by 3 yr data
Consistent with
Inflation and Cold Dark Matter Paradigm
One Puzzle:
Unexpectedly low Quadrupole (l=2)
Measurements of Cosmological
Parameters by WMAP




Bh2 =0.022290.00073 (3% error!)
Mh2 =0.128 0.008
K=0.0140.017 (with H=728km/s/Mpc)
n=0.958 0.016
Spergel et al.
WMAP 3yr alone
Dark Energy
76%
Dark Matter
20%
Baryon 4%
Measurements of Cosmological
Parameters by WMAP




Bh2 =0.022730.00062
Mh2 =0.1326 0.0063
=0.7420.030 (with BAO+SN, 0.72)
n=0.963 0.015
Komatsu et al.
WMAP 5yr alone
Dark Energy
72%
Dark Matter
23%
Baryon 4.6%
Finally Cosmologists Have the
“Standard Model!”

But…
72% of total energy/density is unknown: Dark
Energy
 23% of total energy/density is unknown: Dark
Matter

Dark Energy is perhaps a final piece of the puzzle
for cosmology
equivalent to Higgs for particle physics
Dark Energy

How do we determine =0.76 or 0.72?
Subtraction!: = 1- M - K
Q: Can CMB provide a direct probe of
Dark Energy?
Dark Energy

CMB can be a unique probe of dark energy

1
Temperature Fluctuations are generated by the
growth (decay) of the Large Scale Structure (z~1)
Integrated Sachs-Wolfe Effect
Photon gets blue
Shift due to decay
E=|
-
|
1
2

2
Gravitational Potential of Structure
decays due to Dark Energy
CMB as Dark Energy Probe

Integrated Sachs-Wolfe Effect (ISW)
Induced by large scale structure formation
 Unique Probe of dark energy: dark energy slows down
the growth of structure formation
 Not dominant, hidden within primordial fluctuations
generated during the inflation epoch

Cross-Correlation between CMB and Large Scale
Structure
Only pick up ISW (induced by structure formation)
Various Samples of
CMB-LSS Cross-Correlation
as a function of redshift
w=-0.5
w=-1
w=-2
Measure w!
Less
Than
10min
Cross-Correlation between CMB
and weak lensing

Weak lensing
Distortion of shapes of galaxies due to the
gravitational field of structure
 Can extend to small scales

Non-Linear evolution of structure formation on
small scales
 evolution is more rapid than linear evolution
 rapid evolution makes potential well deeper
 deeper potential well: redshift of CMB
1
Nonlinear Integrated Sachs-Wolfe Effect
Rees-Siama Effect
Photon redshifted
due to growth
 E=|1-2|
2
Gravitational Potential of Structure
evolves due to non-linear effect
Large Scale: Blue-Shift Correlated with Lens
Small Scale: Red-Shift  Anti-Correlated
Nishizawa, Komatsu, Yoshida, Takahashi, NS 08
Cross-Correlation between CMB & Lensing
=0.95,
0.8,
0.74,
0.65,
0.5,
0.35,
0.2,
0.05,

positive
10
negative

l
100
1000
10000
Future experiments (CMB & Large Scale
Structure) will reveal the dark energy!
What else can we learn about
fundamental physics from
WMAP or future Experiments?

Properties of Neutrinos
Numbers of Neutrinos
 Masses of Neutrinos


Fundamental Physical Constants
Fine Structure Constant
 Gravitational Constant

Constraints on Neutrino Properties
Neutrino Numbers Neff and mass m

Change Neff or m modifies the peak heights
and locations of CMB spectrum.
CMB Angular Power Spectrum
Theoretical Prediction
Measure the family
number at z=1000
For Neutrino Mass, CMB with Large Scale
Structure Data provide stringent limit since
Neutrino Components prevent galaxy scale
structure to be formed due to their kinetic energy
Cold Dark Matter
Neutrino as Dark Matter
(Hot Dark Matter)
Numerical Simulation
Constraints on m and Neff
WMAP 3yr Data paper by Spergel et al.
WMAP 5yr Data paper by Komatsu et al.
m  1.5eV(95%CL)
WMAP alone
 0.66eV(95%CL) WMAP+SDSS(BAO)+SN
N  4.4  1.5(68%CL) WMAP+BAO+SN+HST
Constraints on Fundamental
Physical Constants
Fine Structure Constant 
 There are debates whether one has seen variation
of  in QSO absorption lines
 Time variation of  affects on recombination
process and scattering between CMB photons and
electrons
 WMAP 3yr data set:
-0.039</<0.010 (by P.Stefanescu 2007)
Gravitational Constant G


G can couple with Scalar Field (c.f. Super
String motivated theory)
Alternative Gravity theory: Brans-Dicke
/Scalar-Tensor Theory
G  1/ (scalar filed)
 G may be smaller in the early epoch


WMAP data set constrain: |G/G|<0.05 (2)
(Nagata, Chiba, N.S.)
Phase is the Issue


Power Spectrum is OK
How about more detailed structure
Alignment of low multipoles
 Non-Gaussianity
 Cold Spot
 Axis of Evil

Tegmark et al.
• Cleaned Map (different treatment of foreground)
• Contribution from Galactic plane is significant
& obtain slightly larger quadrupole moment.
• alignment of quadrupole and octopole
towards VIRGO?
Recent Hot Topics: NonGaussianity

Fluctuations generated during the inflation
epoch
Quantum Origin
 Gaussian as a first approximation
(x)((x)-)/

0 (x)
Non Gaussianity from Second
Order Perturbations of the
inflationary induced fluctuations

=Linear+ fNL(Linear)2
Linear=O(10-5), non-Gaussianity is tiny!
Amplitude fNL depends on inflation model
[quadratic potential provides fNL =O(10-2)]
Very Tiny Effect:
Fancy analysis (Bispectrum etc) starts to reveal
non-Gaussianity?
First “Detection” in WMAP CMB map
Komatsu et al. WMAP 5 yr.
Cold Spot

Using Wavelet analysis for skewness and
kurtosis, Santander people found cold spots
Kurtosis Coefficient
Only 3-sigma away
This cold spot might be induced by a Super-Void due to ISW
since Rudnick et al. claimed to find a dip in NVSS radio
galaxy number counts in the Cold Spot.
Super Void: One Billion light yr size
Typical Void: *10 Million light yr size
Ongoing, Forthcoming
Experiments

PLANCK is coming soon:
More Frequency Coverage
 Better Angular Resolution


Other Experiments

Ongoing Ground-based:


Upcoming Ground-based:


AMiBA, BICEP, PolarBear, QUEST, CLOVER
Balloon:


CAPMAP, CBI, DASI, KuPID, Polatron
Archeops, BOOMERanG, MAXIPOL
Space:

Inflation Probe
PLANCK vs WMAP
WMAP Frequency
WMAP Frequency Bands
Microwave Band
K
Ka
Q
V
W
Frequency (GHz)
22
30
40
60
90
Wavelength (mm)
13.6 10.0 7.5 5.0 3.3
WMAP Angular Resolution
Frequency 22 GHz 30 GHz 40 GHz 60 GHz 90 GHz
FWHM,
degrees
0.93
0.68
0.53
0.35
<0.23
More Frequencies and better angular resolution
What We expect from PLANCK

More Frequency Coverage
Better Estimation of Foreground Emission (Dust,
Synchrotron etc)
 Sensitivity to the SZ Effect


Better Angular Resolution


Go beyond the third peak, and even reach Silk
Damping: Much Better Estimation of Cosmological
Parameters, and sensitivity to the secondary effect.
Polarization
Gravitational Wave: Probe Inflation
 Reionization: First Star Formation

Polarization
Scattering & CMB quadrupole anisotropies
produce linear polarization
Polarization must exist, because Big Bang existed!
Scattering off photons by Ionized medium
velocity induce polarization:
phase is different from temperature fluct.
• Information of last scattering
Thermal history of the universe, reionization
• Cosmological Parameters
• type of perturbations: scalar, vector, or tensor
Incoming
Electro-Magnetic
Field
Same
Flux
Same Flux
No-Preferred
Direction
UnPolarized
Electron
scattering
Homogeneously Distributed Photons
Incoming
Electro-Magnetic
Field
Strong
Flux
Weak Flux
Preferred
Direction
Polarized
Electron
scattering
Photon Distributions with the Quadrupole Pattern
Power
spectrum
Velocity=
polarization
Wave number
Hu &
White
Scalar
Component
Reionization
Liu et al. ApJ 561 (2001)
First Order Effect
E-mode
2 independent
parity modes
B-mode
Seljak
E-mode
Scalar Perturbations only produce E-mode
Seljak
B-mode
Tensor perturbations produce both E- and B- modes
Scalar
Component
Tensor
Component
Hu & White
Polarization is the ideal probe for
the tensor (gravity wave ) mode
Tensor mode is expected from many inflation models
Consistency Relation
・Tensor Amplitude/Scalar Amplitude
・Tensor Spectral index
・Scalar Spectral Index
You can prove the existence of Inflation!
STAY TUNE!
• PLANCK has been launched!
Higher Angular Resolution, Polarization
• More to Come from grand based and balloon
borne Polarization Experiments