* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download Lesson 7 – Gauss`s Law and Electric Fields
Survey
Document related concepts
Multiferroics wikipedia , lookup
Superconductivity wikipedia , lookup
History of electrochemistry wikipedia , lookup
Eddy current wikipedia , lookup
Hall effect wikipedia , lookup
Electrostatic generator wikipedia , lookup
Magnetic monopole wikipedia , lookup
Electroactive polymers wikipedia , lookup
Nanofluidic circuitry wikipedia , lookup
Lorentz force wikipedia , lookup
Maxwell's equations wikipedia , lookup
Electromotive force wikipedia , lookup
Electric current wikipedia , lookup
Static electricity wikipedia , lookup
Electromagnetic field wikipedia , lookup
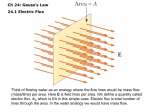
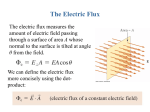
Faraday paradox wikipedia , lookup
Electricity wikipedia , lookup
Transcript
Lesson 7 – Gauss’s Law and Electric Fields © Lawrence B. Rees 2007. You may make a single copy of this document for personal use without written permission. 7.0 Introduction While it is important to gain a solid conceptual foundation of field lines and contours, it is also important to understand electricity and magnetism with mathematical precision. In this chapter, we will translate concepts such as “number of field lines” into mathematical functions and use these results to find the electric fields of several important distributions of charge. This will be our culminating work with electrostatics. 7.1 Gauss's Law of Electricity Let us briefly review a few things about electric fields and electric field lines. Experimentally we know that the Coulomb force between charged particles falls off as 1 / r 2. In Lesson 5 we saw radially directed electric field lines naturally carry this dependence as long we take the field strength to be given by the number of lines per unit area passing through a section of a perpendicular surface. Since we choose the number of field lines going toward a positive point charge or away from a negative point charge to be proportional to the magnitude of the charge, electric field lines geometrically give us the same information that Coulomb’s law gives us algebraically: F ∝ q / r 2 . When there are more complicated arrangements of point charges, the near field and the far field both resemble the fields of single point charges. We have drawn the field lines for several arrangements of charges, so we know how more complicated field lines behave. Think About It A positive point charge alone in space has field lines coming uniformly outward. As a negative charge is brought nearer to it, what happens to the field lines? Does it make any difference what the magnitude of the second charge is? What happens when a positive charge is brought near the first charge? Keeping these facts in mind, let us now think of a box with various unseen charges inside. We are given the task of trying to determine as much as we can about the charges in the box from the electric field lines which extend outside the box. For sake of argument, let us suggest that we draw four field lines for each unit of charge, as we did in Lesson 5. Think About It What can we say about the number of field lines coming out the box or going into the box if a charge of +2 is inside the box? if a charge of −3 is inside the box? if both charges are located very close to each other inside the box? if both charges are located on opposite ends of the box? 1 As you probably deduced, we cannot completely determine the arrangement of charge inside the box by counting the number of field lines outside. A simple charge of +1 will produce almost the same field outside the box as a charge of +187 and a charge of −186 located near each other. Furthermore, if charges +10 and −10 are both located inside the box, some field lines from the positive charge may go directly to the negative charge without ever leaving the box, and some field lines may leave the box from the positive charge and come back in to the negative charge. The one thing we can conclude, however, is that the difference between the total number of field lines leaving the box and the total number of field lines entering the box is four times the net charge within the box. Let me belabor this point a little, just in case the conclusion is not yet obvious. We call let the “net number” of field lines passing through the box be defined as the number of field lines passing out of the box minus the number of field lines entering the box. If there is no charge inside the box but charges located near the box on the outside, each field line that passes into the box passes out of the box again, leaving the net number of field lines equal to zero. If one unit of positive charge is in the box, the net number of field lines is +4 (4 because we arbitrarily chose four lines per unit of charge). If one unit of negative charge is in the box, the net number of field lines is −4. If charges +1 and −1 are both in the box, the field line from the positive charge could do one of two things: 1) they could go to the negative charge without passing out of the box so there would be no contribution to the net number of field lines, or 2) they could leave the box and come back in to the negative charge so each line would contribute +1 to the net number of field lines as it passes out of the box and −1 to the net number as it comes back in. The final result is that the net number of field lines is 0. Continuing this argument, we may conclude that net number of field lines = 4 × the total charge inside. This conclusion, of course, depends neither on the shape nor size of the box. Any closed surface which contains a volume is adequate. Such surfaces are called "Gaussian surfaces." You may safely think of a Gaussian surface as a balloon of any arbitrary shape. Using these definitions of "net number" and "Gaussian surface," we may write the following generalization: Gauss's Law of Electricity The net number of electric field lines passing through a Gaussian surface is proportional to the total charge enclosed by the Gaussian surface. Gauss's law of electricity is the first of Maxwell's equations. Often we refer to it simply as "Gauss's law." The concept is simple − perhaps so simple that it seems useless. However, it forms one of the cornerstones of electromagnetic theory. In the end we must remember that Gauss's law is a direct consequence of the way we construct electric field lines. And electric field lines in turn are a geometric way of representing Coulomb's law. Schematically we may write: Gauss's law 6 electric field lines 6 Coulomb's law. In other words, Gauss's law is nothing more than a different way of expressing Coulomb's law. However, because it is a different way of expressing the same physical content, it can be useful 2 in a completely different set of applications. Later we will find mathematical ways of expressing this concept and use it quantitatively in determining the electric field of several objects. For now, we will find that applying it conceptually can lead to some interesting and useful results. Things to remember: • A Gaussian surface is a closed surface – a surface that encloses a volume. • Gauss's law of electricity: The net number of electric field lines passing through a Gaussian surface is proportional to the total charge enclosed by the Gaussian surface. • Gauss’s law is equivalent to Coulomb’s law because it just an observation based on field lines, and field lines are geometrical representations of Coulomb’s law. 7.2 Charge Density Before we apply Gauss's law, however, we need to define charge density a little more carefully than we did earlier. Actually, we need to define three separate ideas collectively known as “charge density.” When you think of density, you probably think of the mass of a certain amount of material. The most important charge density is "volume charge density." You are probably used to defining mass density as mass per unit volume. Volume charge density is defined analogously to this. For example, a cubic meter of water weighs 1000 kg, so the density of water is 1000 kg/m3. (Or since these are rather large quantities, we usually express the density of water as 1 g/cm3.) We use the Greek letter (rho) to denote volume charge density. Thus = charge / unit volume. ρ You might ask why we should worry about the density of charge at all. Can’t we just express everything in terms of the dimensions of an object and its total charge? If the charge on the object is uniform, sometimes this is true; however, in many objects the charge is not uniformly distributed throughout. In these cases we need a way of expressing just where the charge is located. If q is the charge contained in a small volume v at Cartesian coordinates x, y, and z, we may write the volume density as function of position in the following fashion: ρ ( x, y , z ) = ∆q . ∆v That is, the volume charge density is the charge per unit volume for a small volume located at a specified point in space. In order for to be a "good" function, we really must take the limit of the above expression as v 0; however, this distinction usually is not of significance to us. ρ → (Note: In this text we shall use a lower case v for volume to prevent confusion with electric potential, V.) 3 Think About It Describe in words the following charge densities: 6r 2 , if r ≤ 2 ρ (r ,θ , φ ) = 0, otherwise 3xy, if x < 1, y < 1, z < 1, ρ ( x, y , z ) = 0, otherwise Whereas any massive object will always take up volume, electric charge can be confined to the surface of an object. Since the surface layer is, for all practical purposes, infinitely thin, it becomes impossible to define a volume charge density for the surface. For this type of situation, we define a "surface charge density" as the charge per unit area on a surface. We denote surface charge density by the Greek letter (sigma). σ Think About It Describe in words the following charge densities: σ ( x, y ) = 3 xy cos(θ ), if θ < π − cos(θ ), if θ < π σ (θ , φ ) = Also, charge may be located along a straight line. In that case, we can define the "linear charge density" as the charge per unit length along the line. The linear charge density is represented by the Greek letter (lambda). λ Things to remember; • Charge densities may be volume charge densities (D = charge/volume), surface charge density (F = charge/area), or linear chare density (8 = charge/unit length). 7.3 The Fields of Charge Distributions with Radial Spherical Symmetry Consider a sphere with a charge distribution having radial symmetry. Recall that by our definition of radial spherical symmetry, this means the volume charge density may vary with 4 distance from the origin of a coordinate system, r, but not with angle. We argued earlier that, because of the symmetry of the problem, the electric field lines outside the sphere must be directed radially outward from the origin and be evenly spaced from one another. Because of this, we concluded that the electric field must be the same as the field of a point charge having the same total charge as the sphere. But what can we conclude about the electric field within the sphere? First let us consider a spherical shell with a uniform surface charge density. (This is just a shell, like a balloon or the rubber part of a basketball, with no charge at all inside.) To find the electric field inside the shell we first construct a Gaussian surface within it. Let the Gaussian surface be a sphere of radius r, where r is smaller than the radius of the charged shell. We’ll place the Gaussian surface inside the shell and concentric with it. We know that the net number of field lines passing through this Gaussian surface is proportional to the charge enclosed within the Gaussian surface. But the enclosed charge is zero, so the net number of field lines passing through the surface is also zero! We might be tempted to immediately conclude that the electric field is zero inside the shell; however, we must be careful here because all Gauss's law tells us is that the net number of field lines passing through the surface is zero. This means that the number of field lines entering the sphere must be the same as the number leaving. Fortunately, we can apply symmetry arguments once again. Since the charge distribution is radially symmetric, we know that the electric field lines within the sphere must all be directed either outward or inward. (They cannot lean to one side or another as no side is different from the others. They cannot be partly outward and partly inward as no part of the spherical shell is different from the rest.) If this is true, the only way we can have no net field lines passing through the surface is to have no field lines at all, and hence there is no electric field inside. r Figure 7.1. A Gaussian surface inside a charged basketball. It is important to notice how we used Gauss’s Law in conjunction with symmetry to arrive at this conclusion! 5 r r Figure 7.2. Electric field lines that are impossible because they don’t have radial symmetry. Think About It Coulomb's Law tells us that the closer we are to a point source, the stronger the field must be. Why is it then that if we put a small positive test charge just inside a spherical shell, it isn't repelled toward the center of the shell? Hint: You need to think about all of the charge, not just the closest charge. We can easily see that the same conclusion must apply if the shell is thin or thick. As long as the charge distribution has radial spherical symmetry, the electric field within a hollow sphere must be zero. We can also apply Gauss's law along with symmetry arguments to determine the electric field within a solid sphere having a radially symmetric charge density. By symmetry, we know that the electric field lines are directed radially outward and are evenly spaced. Let us construct a Gaussian surface at a radius r within such a sphere. The number of field lines passing out of this surface is proportional to the charge enclosed by the surface. Hence the electric field is the same as the electric field of a point charge having the same magnitude as the fraction of total charge enclosed within a sphere of radius r. All we have to do is use geometry, perhaps with integration, to determine the enclosed charge. Whenever there is radial spherical symmetry (not necessarily otherwise!), the charge outside the Gaussian surface contributes nothing to the electric field. Mathematically: Electric field inside a spherically symmetric charge distribution (7.1) E= Qenclosed . 4πε 0 r 2 1 6 Things to remember: • We can use Gauss’s law with symmetry to calculate the electric field of spherically symmetric charge distributions. Know how to do that! • Outside the charge distribution, the field is the same as the field of a point charge with the same total charge. • Inside a hollow sphere with a spherically symmetric charge density, the electric field is zero. • At a radius r inside the distribution, the field is the same as the field of a point charge that has the same charge as the charge inside a Gaussian surface of radius r. 7.4 Gauss’s Law and Conductors One other important application of Gauss's law is to electrical conductors. In Lesson 3, we arrived at several rules for conductors. Let’s first review two of those rules: • The static electric field everywhere inside a conductor is zero. • The static electric field on the surface of a conductor is everywhere perpendicular to the surface. Now let us apply Gauss's law. First we construct an arbitrarily shaped Gaussian surface which lies completely within the conductor. Since there is no electric field in the conductor, the net number of electric field lines passing through the surface is zero. By Gauss's law, this implies that the total charge contained within the surfaces is also zero. We can make tiny Gaussian surfaces or large Gaussian surfaces. We can even make a Gaussian surface just barely inside the outside surface of the entire conductor. The total charge in every such surface is zero. In fact, the only place we could find any net charge is on the outside surface of the conductor. Hence, Gauss's law gives us the next important rule for conductors: In a static situation, all net charge on a solid conductor must lie on its outer surface. We argued that this result was true in Lesson 3, but we didn’t have the tools to construct a rigorous proof at that time. Figure 7.3. Any Gaussian surface within a conductor contains zero net charge. 7 Think About It What can you say about the charge in a conductor if there is a hollow bubble inside the conductor? What if there is a charge within a hollow bubble inside a conductor? If there is a bubble within a conductor, we can place a Gaussian surface just inside the conductor around the bubble. Since E = 0 everywhere on the Gaussian surface, no net field lines pass through the surface, so the total enclosed charge must be zero. That doesn’t preclude some positive surface charge on one side of the bubble and some negative surface charge on the other side; however, if there are no fields to keep the charge separated, charge will flow until the surface of the bubble is neutral everywhere. On the other hand, if there is a positive charge in the middle of the bubble, there must be a negative surface charge on the bubble so that the total charge inside the Gaussian surface remains zero. We see that the charge in a conductor can and must arrange itself on the conductor’s surface in such a fashion that it sets up a field of its own which 1) is equal and opposite to the external electric field everywhere inside the conductor and 2) is equal and opposite the component of the electric field parallel to the surface of the conductor everywhere on the surface. Things to remember: • In a static situation, all net charge on a conductor must lie on its outer surface. • Know how to prove that this is true using Guass’s law in conjunction with the fact that the static electric field inside a conductor is zero. 7.5 Gauss's Law of Magnetism If such a thing as magnetic charge were to exist, and magnetic charge obeyed a 1 / r 2 type force law, as we would be expect the magnetic field to obey a law much like Gauss's law of electricity. That is, the net number of magnetic field lines passing through a Gaussian surface must be proportional to the magnetic charge enclosed within the surface. Since there are no known magnetic charges, Gauss's law of magnetism is: Gauss's Law of Magnetism The net number of magnetic field lines passing through a Gaussian surface is always zero. This implies that for every possible Gaussian surface we can construct, whenever a magnetic field line enters the surface, it has to pass out of the surface as well. The only way this can happen is if every magnetic field line forms a closed loop. This is a very important result you need to remember! 8 Gauss's law of magnetism is the second of Maxwell's equations. It is equivalent to the experimental observation that there are no magnetic monopoles – a magnet can’t have a north pole without a south pole. Things to remember: • Magnetic field lines always form closed loops. • Gauss's Law of Magnetism: the net number of magnetic field lines passing through a Gaussian surface is always zero. 7.6 Uniform and Non-uniform Densities In Section 7.3, we found the electric field inside or outside any spherically symmetric 1 Q(inside radius r ) charge distribution is given by Eq. (7.1): E (r ) = . All we need to know 4πε 0 r2 to solve the problem is the total charge within a spherical Gaussian surface of radius r. Example 7.1. Uniform Spherical Charge Distribution What is the electric field inside a sphere of radius a having total charge Q if the charge distribution within the sphere is uniform? We need to find how much of the sphere’s charge is located within a radius r to solve this problem. Since the charge density is uniform, we can use the relationship ρ= Qenclosed . Venclosed This relationship holds equally well at radius a and radius r. Thus: Q Q ρ= = enclosed 4 4 3 π a3 πr 3 3 r ⇒ Qenclosed = Q a 3 3 1 Qr r 1 E (r < a) = Q 2 = 4πε 0 a r 4πε 0 a 3 1 Notice that the electric field inside the sphere increases linearly with radius. This is because the volume of charge that contributes to the electric field is proportional to r 3 while the Coulomb force drops off as 1 / r 2 . 9 If the density varies with position, however, finding the total charge is not so simple. Let us again consider a volume charge density. Even if the density varies over a sphere, the density in one very small region within the sphere is nearly constant. Thus the charge q within a small r volume, V, located at the position r is just r ∆ q = ρ (r ) ∆V If we want to know the total charge on the object, we have to divide the entire sphere into small elements of volume. Each volume element must have a density that is (nearly) constant. We then must add up all the contributions from each element to obtain the total charge. That is: r q = ∑ dq = ∑ ρ (r ) ∆V . Of course, this expression is only approximate unless we let the size of each volume element shrink to zero. In this limit, the sum becomes an integral and r q = ∫ dq = ∫ ρ (r ) dV . Similar relationships apply to surface charge densities and linear charge densities: r q = ∫ dq = ∫ σ (r ) dA, q = ∫ dq = ∫ λ ( x ) dx . Often we also need to know the total volume or area of a region. To find the total volume, for example, all we need to do is add up all the elemental volumes: V = ∫ dV . Sometimes students panic at the mention of integrals; however, there are three things you must keep in mind: 1) An integral is conceptually nothing more than a sum. In fact, the symbol is just the letter "s" (for sum) as used in printing fonts until about 1800. 2) Integrals are often much easier to evaluate than the corresponding summations. 3) Integrals are tabulated in tables so we usually do not have to resort to the clever methods you learned in calculus classes to evaluate them. Things to remember: • You can use Coulomb’s law to find the electric field at radius r for any spherically symmetric charge distribution as long as you remember that the charge that contributes to the field is only the charge on the inside of a sphere of radius r. • In general, you can find the enclosed charge by integrating over the charge density: q = ∫ ρ dV . 7.7 Two-dimensional Integration Most of the integrals we will need to evaluate are in either two or three dimensions. You probably do not feel very confident about evaluating such integrals; however, if you can 10 visualize what you are integrating, you can always set up the correct integral. To illustrate this point, let us begin with integration over surfaces. First of all, let us consider a rectangle with corners (0,0), (b,0), (b,c), and (0,c) in Cartesian coordinates, as shown below. y c x b Figure 7.4 The “standard” rectangle Let’s find the total area of the rectangle. Of course, we know A = bc; however, we will find A by integration. All we have to do is add up the elements of area to get the whole. Thus A = ∫ dA . What we do now is the most difficult part of any integration. We have to slice up the region; that is, we have to decide how to choose the elemental areas dA. At this point it is important to remember that an integral is just a sum. Any way in which we can draw small areas and can find dA for each of these areas is acceptable. In calculus classes you probably learned to divide such a rectangle into small rectangles. We draw one arbitrary rectangle in the larger rectangle, as shown in Fig. 7.5. We denote the length of the sides by dx and dy. Then we can see that dA = dx dy. To finish the integration, we need to find the limits of integration. These clearly extend in the x direction form 0 to b and in the y direction from 0 to c. Thus: c b A = ∫ dA = ∫ ∫ dxdy = bc 0 0 11 y c dy dx x b Figure 7.5 Slicing the rectangle in both x and y directions. There’s nothing wrong with slicing the rectangle into dx dy areas; however, it is often possible to reduce a two-dimensional or three-dimensional integral into a one-dimensional integral by looking at the details of the problem. In this problem, we could slice the rectangle along the x direction as shown in Fig. 7.6, or along the y direction as shown in Fig. 7.7. In these cases the areas are dA = c dx and dA = b dy. The integrals are then evaluated by simply adding up the dAs: b A = ∫ dA = ∫ c dx = bc or 0 c A = ∫ dA = ∫ b dy = bc. 0 12 y c x dx b Figure 7.6 Slicing the rectangle along the x direction. y c dy x b Figure 7.7 Slicing the rectangle along the y direction. The answer is the same no matter how we do it, but the integral is easier to evaluate when we reduce it to a one-dimensional integral. 13 Think About It How many other ways can you slice the rectangle into small areas dA? What is the value for dA in each case? Of course, this case was trivial as we knew the answer from the beginning. Let us do a more complicated problem now. We take the same rectangle as in Fig. 7.4; however, let us find the total charge on the rectangle when the surface charge density is given by the function (x) = Kx2, where K is a constant. We then slice the rectangle into small units of area dA with charge (x) dA. We know that the total charge is just q = ∫ dq = ∫ σ dA . Now let's look at how we could σ σ slice the rectangle. If we slice the rectangle in both the x and y directions, the area is dA = dx dy and the charge on the slice is dq = K x 2 dx dy . We could then evaluate the integral using the same limits as above. The only difference is that the integrand is now a function of x. c b q = K ∫ ∫ x 2 dx dy = 0 0 σ 1 Kcb 3 3 If we slice the rectangle along the y axis, we write dA = b dy for the area and dq = (x) b dy for the charge on this area. But there is one problem. What is the value of on this slice? Since the charge density varies with x, the slice has much more charge on the right side than on the left. When we write dq = da for a slice, must be a constant on the slice! That is, the simple expression (charge) = (surface charge density) × (area) is only valid when the density is constant. We can draw an extremely important conclusion from this: σ σ σ Slicing Rule You must integrate over all variables which appear in the integrand, being careful not to ignore variables "hidden" in functions. Here, the integrand has an x appearing in it, so we must integrate over dx. Slicing the region into smaller rectangles, as in Fig. 7.5, is fine because we do integrate over dx. However, since y does not appear in the integrand, we don’t need to integrate over dy. This means we can find a simpler way to slice the rectangle so we only integrate over dx. The clear choice is to slice the rectangle as in Fig. 7.6. Here dA = c dx and dq = Kx 2 c dx. Thus, we find the charge by integrating over dx: b 1 q = ∫ dq = Kc ∫ x 2 dx = Kcb 3 . 3 0 14 Be sure that you thoroughly understand the above examples. If you do, then you will have little trouble with more complicated problems. Think About It What is the total charge on the "standard" rectangle when the charge density is = C y and when = D x y where C and D are constants? σ σ Because of the nature of fields, very few problems involve integration over rectangles. In two dimensions, almost all integrals will be in polar coordinates, r and . In polar coordinates there are two principle ways of slicing a circle: in concentric rings or in wedges. θ In Fig. 7.8 we slice the circle in rings. A typical slice at radius r and with width dr is illustrated. Keep in mind that dr is very small, and in fact goes to zero in the limit, although we draw it much thicker. We then need to calculate the area dA of the ring. To do this, let us mentally take a pair of scissors, cut the ring and stretch it out straight. Since dr is very small, the stretched-out ring very nearly forms a rectangle of length 2 r and width dr. Thus the area of an annular ring is just π (7.2 Area of an annular ring) dA = 2π r dr . dr a r dr 2 Br Figure 7.8 Slicing a disk into annular rings. 15 We can then integrate to get the total area of the circle: a A = ∫ dA = 2π ∫ r dr = π a 2 . 0 Notice that for any integrand which depends only on r, this is the appropriate way to slice the disk. For almost all applications using polar coordinates in this book, we will make use of this technique, so learn it well! Example 7.2. A disk of radius a has a surface charge density = C r where C is a constant. Find the total charge on the disk. σ a 2 q = ∫ dq = ∫ σ dA = 2π C ∫ r 2 dr = πC a 3 . 3 0 The second way of slicing a circle is in wedges, as shown in Fig. 7.9. This time the area of the wedge is approximately that of a triangle with base a d (remember arc length is angle times radius) and height a. Thus θ dA = ½ a 2 d . θ Again, we can integrate over d to find the total area of the circle. θ 2π 1 A = a 2 ∫ dθ = π a 2 . 2 0 This, of course, is the appropriate way to slice a circle whenever the integrand is only a function of . θ 16 d2 a 2 Figure 7.9 Slicing a disk into wedges. Think About It When the integrand depends on both r and , show that the area of an appropriate slice is dA = r dr d . θ θ Things to remember: • By appropriate slicing of areas and volumes, you reduce many integrals to a simpler form. • You must integrate, however, over all variables that appear in the integrand. • If you slice a disk into annular rings, the area of each ring is dA = 2π r dr. 7.8 Three-dimensional Integration It becomes somewhat more complicated to consider integration in three dimensions rather than two; however, the basic principles are the same. In Cartesian coordinates, the conversion from two to three dimensions is trivial. Here the volume element is just dV = dx dy dz. If we have a rectangular prism (a box shape, that is), we can find which coordinates appear in the integrand and slice the prism into elements of volume appropriately. Think About It What is the total charge of a cube of length 1 m on each side if the charge density is = A z where A = 3 C/m4 and z is the distance from one specific face of the cube? ρ 17 In cylindrical coordinates, integration is very similar to polar coordinates. Let us find the volume of a cylinder of length and radius R. We put the center of one end the cylinder on the origin and its axis along the z axis. Now we have to divide the cylinder into elemental volumes. If the integrand only depends on r, the usual case, the appropriate way of doing this is by slicing the cylinder into cylindrical shells. That is, we slice the cylinder with each volume element being a “hollow pipe”. The volume of such a cylindrical shell is just the volume of a pipe (not the volume inside the pipe) of length , radius r, and wall thickness dr. This is just ℓ ℓ dV = 2 r dr. π ℓ Notice that we have converted a three-dimensional integral into a one-dimensional integral. The integration is straightforward: R V = ∫ dV = 2π l ∫ r dr = π R 2 l . 0 In spherical coordinates, we will mostly deal with integrands which are functions of r only. In this case, we must slice the sphere into concentric spherical shells. We may think of a typical shell of radius r and thickness dr as being similar to an orange peel. If we cut such a peel off an orange and spread it out flat, it is clear that the volume will be approximately the thickness of the peel times its surface area. Thus we have dV = 4 r 2 dr. π We obtain the total volume of the sphere by integrating r from 0 to the radius of the sphere, R. This becomes R 4 V = ∫ dV = 4π ∫ r 2 dr = π R 3 . 3 0 Rather than memorizing the formulas for different classes of integrals, you should work through a large number of examples until you have a feeling for how to set up integrals. To find total charge, we need only remember the definition of the different charge densities to get dq : λ dq = d in one dimension dq = dA in two dimensions dq = dV in three dimensions. ℓ σ ρ Things to remember: • The volume of a cylindrical shell is 2π rl dr . • The volume of a spherical shell is 4π r 2 dr . • Memorize these expressions, as we will make frequent use of them! 18 7.9 Gauss's Law and Electric Flux The electric field of any charge distribution could be determined by summing up the contributions of all its component charges. We essentially did this when we integrated over threads in Lesson 1. However, there are a very limited number of cases for which closed-form solutions are obtainable by direct integration. Earlier in this chapter, we learned how we can use Gauss's law in conjunction with symmetry considerations to determine the electric fields of charge distributions with radial spherical symmetry. Gauss's law can also be used to calculate the electric fields of several other types of charge distribution. Previously we used Gauss's law as a qualitative help in making our arguments. At this point, we will construct a mathematical form for Gauss's law so that we can use it more precisely. We know that Gauss's law states: "The net number of electric field lines passing through a Gaussian surface is dependent only on the charge contained within the surface." We also know that one of the fundamental characteristics of electric field lines is that the number of field lines per unit area is proportional to the strength of the field. We must now turn this idea into a mathematical expression. r A Figure 7.10 Electric field lines passing through a frame perpendicular to the field. Φ = EA. Let’s take a uniform electric field pointing in the x direction. We may visualize the electric field passing through a "picture frame" which is oriented so that the electric field is perpendicular to the plane of the frame. The area of the frame is A. We know that the magnitude of the field, E, is given by the relation: E∝ number of field lines , A 19 or, solving for the number of field lines passing through the frame, number of field lines % EA. Since we tend to be more comfortable working with equalities than proportionalities, let us rewrite this as number of field lines = kEA where k is a constant that depends on the number of field lines we wish to associate with each Coulomb of charge. We call the quantity EA the "electric flux" and denote it with an upper case phi, . Φ (7.3 Flux through a perpendicular frame) Φ = EA In terms of flux, number of field lines = k . Φ If we’re not particularly worried about the value of the constant k, we can think of the flux as just the “number of field lines.” The units of flux are ( V / m ) × ( m 2 ) = V m. r A θ Figure 7.11 Flux through a tilted frame. Φ = EA cos . θ This is perfectly good if the plane of the frame is perpendicular to the field lines; however, if the plane is tilted with respect to the field, the number of field lines passing through the frame is reduced. To account for this effect, it is convenient to use the definition of the “area vector.” To give a direction to an area, we choose a unit vector that is perpendicular to the 20 surface. (A unit vector lying in the surface of the plane could point in any number of directions!) Let us denote by the angle between this unit vector and the electric field. For a perpendicular plane, = 0, or the field is parallel to the area vector. With this definition of , we see that the number of field lines passing through the frame must be proportional to cos . Thus: θ θ θ θ (7.4 Flux through a tilted frame) Φ = EA cos . θ We can write this result in a shorter form by using the dot product. The meaning is no different, however: r r Φ = E ⋅ A. Think About It There are really two directions which are perpendicular to the frame, so there are two equally logical choices for the area vector. Does it make any difference which one we choose? This formula is getting better, but it is still only useful when the electric field is a constant over the area of the frame. If the electric field is non-uniform, we can divide the area into small pieces, dA. As long as dA is small enough that E is nearly constant, we know the flux through dA is r r dΦ = E ⋅ dA . The total flux through the area is then just the sum over all such contributions. Finally, we have a general equation for flux, or the number of field lines passing through an area: Electric Flux (7.5) where r r Φ = ∫ dΦ = ∫ E ⋅ dA Φ is the electric flux passing through a surface. It has units of volt meters (Vm). r E is the electric field in volts/meter (V/m). r dA is an element of area on the surface over which we integrate. The direction of the area is normal (perpendicular) to the surface. r r Note that we must take the dot product of E and dA for each slice of area. In general, this is a very complicated integral. You should thoroughly understand what it means, but I don’t expect you to have any idea how to evaluate this kind of integral in general. 21 Things to remember: • The mathematical function that describes the number of field lines is called the flux. •You should remember that flux is essentially field H area. • In general, we need to account for the angle of the surface with respect to the field and non-uniformities in the field when we calculate the flux. r r • Know the formal definition of flux Φ = ∫ E ⋅ dA 7.10 The Integral Form of Gauss's Law Gauss's law says that the number of electric field lines passing through a Gaussian surface is proportional to the charge enclosed within the surface. Now that we have a mathematical expression for the flux and know that flux is proportional to the number of field lines, we can write Gauss's law simply: = b q enc Φ where is the total flux through the Gaussian surface, b is a constant, and q enc is the total charge enclosed within the surface. In turn, we can write the flux as Φ r r Φ = ∫ E ⋅ dA ∫ means integration over the entire closed (Gaussian) surface. When we have r closed surfaces, we always define the direction of dA to be perpendicular to the surface and directed outward from the enclosed volume. where the symbol To see how Gauss’s law works, let’s apply it to a point charge, q. We know the electric field of a point charge, so we can directly evaluate the flux. Gauss’s law works for any Gaussian surface, but we want to make the choice of surface as easy as possible, so let’s use a sphere of r r radius a. Because the electric field is perpendicular to the sphere everywhere, E ⋅ dA is just E dA. We then can substitute the Coulomb's law expression for E into the integral. We then have: r r Φ = ∫ E ⋅ dA = ∫ EdA = q q 1 q dA = 4πa 2 = 2 ∫ 2 4πε 0 a 4πε 0 a ε0 1 As we noted above, Gauss's Law tells us that = b q enc. Since we have a point charge, the enclosed charge is all of q. Comparing the two results, we see that the constant b = 1 / 0 . Φ ε 22 Knowing this constant, we can write Gauss's law in its integral form: Gauss's Law of Electricity (7.6) r r q Φ E = ∫ E ⋅ dA = enc ε0 In this form, Gauss's law looks quite complicated. There are a few things, however, we should keep in mind. First, the concept embodied in this mathematical form is just the same as we have already known: the net number of electric field lines passing through a Gaussian surface is proportional to the enclosed charge. Secondly, Gauss's law − even in integral form − is another way of stating the physics of Coulomb's law. Thirdly, we will only evaluate the flux integral in cases where it is very simple. Before we discuss uses of Gauss's law, we should emphasize one thing: Gauss's law is always true, even if we do not know how to evaluate the integral. If we put a charge q0 inside a sphere, the flux through the surface of the sphere is q0 / 0. If we put a charge q0 inside a cube, the flux through the surface of the cube is q0 / 0. If we put a charge q0 inside a tetrahedron, the flux through the surface of the tetrahedron is q0 / 0. Therefore, if you are asked to find a flux through a surface, you need not evaluate a complicated integral as long as you know the total charge contained within the surface! ε ε ε Think About It When we discussed Gauss's law earlier, we defined the net number of field lines passing through a surface as the "number of field lines coming out of the surface minus the number coming in." How does the flux integral incorporate this concept? Things to remember: • Gauss’s law is always true. r r q • Gauss’s law in integral form is Φ E = ∫ E ⋅ dA = enc . This is just a mathematical way of ε0 saying that the net number of electric field lines passing through a Gaussian surface is proportional to the charge enclosed in the surface 7.11 Applying Gauss's Law By Gauss's law, if we know the electric field everywhere on a closed surface, we can deduce how much charge is contained within the surface. Usually, however, we know the 23 distribution of charge and we want to find the electric field. Unfortunately we can not often use Gauss's law to do that. In a few cases where there is a high degree of symmetry; however, Gauss's law can be used to find electric fields. To do this, there are two conditions that must be met: • We must choose the Gaussian surface such that the electric field is perpendicular to the surface r r (that is, E is parallel to dA ). This allows us to simplify the integrand: r r E ⋅ dA = E dA. Note that if the Gaussian surface is perpendicular to the electric field, the Gaussian surface must also be an element of a field contour. • The problem must have symmetry such that the magnitude of the electric field is constant over the entire surface (or at least the entire part of the surface through which flux passes). With these simplifications, the flux integrals becomes r r Φ = ∫ E ⋅ dA = ∫ E dA = E ∫ dA = EA . In other words, for these special conditions – and these conditions include everything we’re going to do – the flux reduces to what we said it was in the beginning: Electric Flux – the Practical Form Φ = EA . (7.7) This means that we can write Gauss’s law as: Gauss’s Law – the Practical Form (7.8) EA = q enc ε0 . where we choose a Gaussian surface that is perpendicular to the field and on which the electric field is uniform (only cases of high symmetry), and E is the electric field on the Gaussian surface in volts/meter (V/m). A is the area of the Gaussian surface in square meters (m2). ε 0 is the permittivity of free space. q enc is the total charge enclosed in the Gaussian surface. It has units of coulombs (C). 24 One of the most important things for you to learn this semester is how to apply Gauss’s law in the few cases where there is enough symmetry that we can use Eq. 7.8. We will now go over each of these cases in turn. Be sure you can reproduce these examples in detail! A. Charge Distribution with Radial Spherical Symmetry A sphere of radius a has a volume charge density ρ (r ) that has radial spherical symmetry. Because of this symmetry, we recognize that the field is radial and that the perpendicular (equipotential) surfaces are concentric spheres. Furthermore, the magnitude of the electric field must be the same at every point on the spherical surface. We choose a sphere of radius r as the Gaussian surface. It has an area of A = 4 r 2. Thus, π E= q enc 1 1 qenc = ε 0 A 4πε 0 r 2 1 1 = 4πε 0 r 2 1 = ε0 r2 rmax ∫ ρ (r )4π r 2 dr 0 rmax ∫ ρ (r ) r 2 dr 0 It is important to remember that A is the area of the Gaussian surface and that the integral is over all the volume included within the Gaussian surface. If we want to find the electric field inside the charge distribution where r<a, then rmax = r. If, however, we want to find the electric field outside the charge distribution where r>a, then rmax = a, the radius of the charge distribution. If we’re finding the field on the outside of the charge distribution, we stop integrating at a because there is no charge at r larger than a. Note that this is the same conclusion we reached earlier using qualitative arguments. r r a a (a) (b) Figure 7.12 Choosing a Gaussian surface to find the E field inside (a) and outside (b) a spherically symmetric charge distribution. The region of integration is the cross-hatched green area. 25 B. Charge Distribution with Radial Cylindrical Symmetry Let us now find the electric field of an infinitely long cylinder of charge. The perpendicular (equipotential) surfaces are now concentric cylinders. Since it is difficult to work with infinitely long Gaussian surfaces, let us take just as a Gaussian surface a cylindrical shell of length and radius r. A Gaussian surface must be a closed surface, so it must include the ends of the cylinder also. By symmetry, we know that the electric field lines must radiate directly outward from the axis of the cylinder. This means that no electric field lines pass through the ends of the cylinder. Because of this, only the "sides" of the cylinder contribute to the flux. Furthermore, on the sides of the cylinder, the electric field has constant magnitude. Because of that, the flux simplifies to EA with A = 2 r . Thus: π ℓ E= qenc 1 1 qenc = ε 0 A 2πε 0 rl = = 1 1 2πε 0 rl 1 ε0 r rmax ∫ ρ (r )2π rl dr 0 rmax ∫ ρ (r )r dr 0 Note that the length of the Gaussian surface, l , divides out of the problem, so the length of our Gaussian surface really doesn’t matter. r l C. Infinite Plane of Charge One other geometry with sufficient symmetry to apply Gauss's law is an infinite sheet of charge. Let the surface charge density of the plane be . Here, symmetry requires the electric σ 26 field to be perpendicular to the plane everywhere in space. There can be no component up or down, left or right, as there is nothing special about any given direction. The perpendicular surfaces are planes parallel to the charged plane. We can construct as a Gaussian surface anything that has two surfaces parallel to the plane; a cube of side a is a simple choice. We orient the cube so that the plane passes through the cube's center with two faces parallel to the plane. Because the electric field is pointing outward from the plane, the only flux is through the surfaces parallel to the plane. Each surface has outward (hence positive) flux of Ea 2, so the net flux is twice that. The charge enclosed in the cube is q enc = a 2. Gauss's law then gives: σ E= σ a2 σ . = 2 2ε 0 ε 0 2a Note that this is a constant, depending only on the surface charge density. The field doesn’t get weaker as you move away from the plane. This is consistent with the fact that the electric field lines don’t get farther apart as we move away from the plane. E a Figure 7.7 Gaussian surface for a planar charge distribution. D. Infinite Conducting Sheet If, instead of an infinite plane of charge, we have an infinite conducting sheet with a surface charge density of (on one surface of the conductor), we can also find the electric field. The only thing different from the previous case is that in the conducting material there is no electric field. Instead of placing the cube so that the faces are outside the plane, we can place the cube with one face in the conductor and one outside. Thus the net flux out of the cube is Ea 2, there being only one surface with field passing through it. The result then is twice the previous result: σ 27 E= σ ε0 The factor of 2 results because, in a conducting plane, each outside surface must have a surface charge density of . This is because the charges repel and distribute out evenly over both surfaces. A conducting plane is then like two non-conducting parallel planes placed close to each other. σ E. Some Geometrical Conclusions Notice that Gauss's law tells us that the total electric flux is independent of distance from a charge. Another way of stating this is that electric field lines can only be created or destroyed on charges. The area of spherical Gaussian surfaces goes as r 2, so the electric field must go as r −2 to keep the flux constant. In general, we can conclude that the electric field must always be inversely proportional to the area of a Gaussian surface. The following table summarizes this for the cases we have considered in this chapter: Source of Charge Dimensionality of Source Dependence of Surface Area Dependence of Field Point 0 r2 r −2 Line 1 r1 r −1 Plane 2 r0 r0 Things to remember: • In a few cases of high symmetry, Gauss’s Law reduces to EA = q enc ε0 . • These cases are limited to charge distributions with spherical, cylindrical, or planar symmetry. • In these cases, we can use Gauss’s Law to find electric fields. The only tricky part is integrating over the charge distribution to find the enclosed charge. • This is a very important section. Know it well! 28