Download Newton`s Second Law:

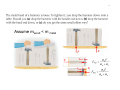
Newton’s Second Law:
1
A force action on a body gives it an acceleration which is in the direction
of the force and has a magnitude given by mass times acceleration

 F is the net force
 This is the vector sum of all the forces acting on the object.
 total force, resultant force, or the unbalanced force.
Newton’s Second Law can be expressed in terms of components:
 The sum of the forces is equated to this product of the mass of the object
and its acceleration.
The SI unit of force is the Newton (N).
 1 N = 1 kg·m / s2
1 N ~ ¼ lb
Second Law
Suppose I have a tennis ball in my hands. It's
not being accelerated in our reference frame.
2
3
A hockey puck having a mass of 0.30kg slides on the frictionless, horizontal surface of an ice rink. Two hockey sticks strike
the puck simultaneously, exerting the forces on the puck.
The force
The force
has a magnitude of 5.0 N
has a magnitude of 8.0 N
Determine both the magnitude and the direction of the
Puck’s acceleration.
1) Determine the Net Force
2) Using Newton’s 2nd law, the acceleration can
be calculated
4
Find the component of the net force acting on
the puck in the x direction
Find the component of the net force acting
on the puck in the y direction
Use Newton’s 2nd Law to find the x and y
component of the puck’s acceleration
magnitude
direction
5
Weight vs Mass
The life support unit strapped to the back of
astronaut Harrison Schmitt weighted 300lbs
on Earth and had a mass of 138 kg.
During his training, 50lbs mock-up with
a mass of 23kg was used
Although this strategy effectively
simulated the reduced weight, it did not
correctly mimic the unchanging mass
It was more difficult to accelerate the 135
kg unit (perhaps by jumping or twisting
suddenly) on the moon than it was to
accelerate the 23kg unit on the Earth
Force of gravity
6
Motion
7
Newton’s Third Law
The mutual forces of action and reaction
between two bodies
are equal and opposite.

If two objects interact, the force F12 exerted by object
 1 on object 2 is equal in
magnitude and opposite in direction to the force F exerted by object 2 on object 1.


 F12  F21
21
 Note on notation:

FAB is the force exerted by A on B.
FORCES ALWAYS COME IN PAIRS, ACTING ON
DIFFERENT OBJECTS:
THESE FORCES ARE CALLED ACTION-REACTION PAIRS.
Physics with a New York attitude
Hey, You push me!! I push you back!!
1
2
We exert a Force by contact is equal in magnitude and opposite in direction to the Force exerted by box on the hand. If we are interested only in the motion of the box, we do not care about the Forces the
box applies to the hand, only the Forces are applied to the box
However since the force pairs are equal in magnitude due to N3, the reaction forces of the
object of interest gives us direct information about the forces that are applied to the object.
10
What are the consequences of N3 when an
external force is applied to objects in contact
The 2 box masses are in contact
consequently acceleration must be the same
m1
m2
F12
F21
a
a
F12
a
F21
a
11
Assume mwood < m metal
F
FWM FMW
FWM FMW
F
Fan Demonstration
12
F – fan blades
FFA
N3 law
FAF
FFA=-FAF
A – air
S – shield
C – cart + fan
N2 law
FFA
If the path between the fan
blades and shield is short,
we can make the assumption
FAS
FAF
FSA
The net forces acting on the cart
Shields up
13