* Your assessment is very important for improving the workof artificial intelligence, which forms the content of this project
Download physical chemistry lecture 3
Thermal radiation wikipedia , lookup
Temperature wikipedia , lookup
Equipartition theorem wikipedia , lookup
R-value (insulation) wikipedia , lookup
Calorimetry wikipedia , lookup
Thermoregulation wikipedia , lookup
Heat capacity wikipedia , lookup
Heat equation wikipedia , lookup
Heat transfer wikipedia , lookup
Second law of thermodynamics wikipedia , lookup
Chemical thermodynamics wikipedia , lookup
First law of thermodynamics wikipedia , lookup
Thermodynamic system wikipedia , lookup
Thermal conduction wikipedia , lookup
Conservation of energy wikipedia , lookup
Internal energy wikipedia , lookup
Heat transfer physics wikipedia , lookup
Gibbs free energy wikipedia , lookup
Thermodynamic temperature wikipedia , lookup
Adiabatic process wikipedia , lookup
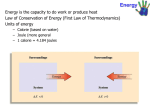
Basic concept: 1. Work, heat and energy 2. The internal energy 3. Expansion work 4. Heat transaction 5. Adiabatic changes Thermochemistry: 1. Standard enthalpy changes 2. Standard enthalpies of formation 3. The temperature dependence of reaction enthalpies. First Law Thermodynamic State of function and exact differentials: 1. Exact and inexact differentials 2. Changes in internal energy 3. The Joule – Thomson effect Work • Work (w) is defined as the force (F) that produces the movement of an object through a distance (d): Work = force × distance w=Fxd • Work also has units of J, kJ, cal, kcal, Cal, etc. • The two most important types of chemical work are: – the electrical work done by moving charged particles. – the expansion work done as a result of a volume change in a system, particularly from an expanding or contracting gas. This is also known as pressure-volume work, or PV work. • PV work occurs when the force is the result of a volume change against an external pressure. The example of PV work – in the cylinder of an automobile engine The combustion of the gasoline causes gases within the cylinder to expand, pushing the piston outward and ultimately moving the wheel of the car. The relationship between a volume change (∆V) and work (w): W= -P ∆V Where P is external pressure The units of PV work are L·atm; 1 L·atm = 101.3 J. • If the gas expands, ΔV is positive, and the work term will have a negative sign (work energy is leaving the system). • If the gas contracts, ΔV is negative, and the work term will have a positive sign (work energy is entering the system). • If there is no change in volume, ΔV = 0, and there is no work done. (This occurs in reactions in which there is no change in the number of moles of gas.) Expansion Work • If the gas expands, ΔV is positive, and the work term will have a negative sign (work energy is leaving the system). • If the gas contracts, ΔV is negative, and the work term will have a positive sign (work energy is entering the system). • If there is no change in volume, ΔV = 0, and there is no work done. (This occurs in reactions in which there is no change in the number of moles of gas.) b) Free expansion is expansion against zero opposing force. W=0 No work is done when a system expand freely. Expansion of this kind occurs when a gas expands into a vacuum. c) Expansion against constant pressure – now suppose that the external pressure is constant throughout expansion. Therefore, if we write the change in volume as ∆V=Vf -Vi d) Reversible Expansion A reverse change in thermodynamic is a change that can be reversed by an infinitesimal modification of a variable. The key “infinitesimal” sharpen the everyday meaning of the word “reversible” as something that can change direction. d) Isothermal reversible expansion • When the volume is greater than the initial volume, as in expansion, the logarithm in above equation is positive and hence w<0. In this case the system has done work on the surroundings and there is a corresponding reduction in its internal energy. • From the equation also show that more work is done for a given change of volume when temperature is increased: at higher temperature the greater pressure of the confined gas needs a higher opposing pressure to ensure reversibility and the work done is correspondingly greater. Table 1 Type of work Type of work Variables Conventional unit Volume expansion Pressure (P), volume (V) Pa m3 = J Stretching Tension (ɤ), length (l) N m= J Surface expansion Surface tension (ɤ), area (σ) (Nm-1)(m2) = J Electrical Electrical potential(φ), Electrical change (q) VC=J Example 1: Inflating balloon requires the inflator to do pressure-work on the surroundings. If balloons is inflated from a volume of 0.100L to 1.85L against an external pressure of 1.00 atm, how much work is done (in joules)? Sort: you are given the initial and final volumes of the volumes of the balloon and the pressure against which its expands. The balloon and its contents are the system Given: V1 = 0.100L, V2 = 1.85L, P=1.00 atm Find: W Strategy: the equation W= -P ∆V specifies the amount of work done during a volume Change against an external pressure. Conceptual Plan: P,∆V → W W= -P ∆V Solve: To solve the problem, compute the Solution: value of ∆V and substitute it, together with ∆V = V1 - V2 P, into the equation. = 1.85L - 0.100L = 1.75L W= -P ∆V = - 1.00 atm x 1.75L = -1.75L.atm The units of the answer (L.atm) can be -1.75 L.atm x 101.3 J = -177 J converted to joules using 101.3J = 1L.atm 1L.atm Check : The units (J) are correct for work. The sign it should be for an expansion: work is done on the surroundings by the expanding balloon. Example 2: A sample of argon of mass 6.56 g occupies 18.5 dm3 at 305K. (a)Calculate the work done when the gas expands isothermally against a constant external pressure of 7.7 kPa until its volume has increased by 2.5 dm3. (b) Calculate the work that would be done if the same expansion occurred reversibly. (a) (b) HEAT Heat is a exchange of thermal energy between a system and its surroundings caused by temperature difference. Notice the distinction between heat and temperature. Temperature is a measure of the thermal energy of a sample matter. Heat is transfer of the thermal energy. Temperature Change and Heat Capacity – when system absorbs heat (q) its temperature changes by ∆T: Heat (q) System ∆T Experimental measurements demonstrate that the heat absorbed by a system and its corresponding temperature change are directly proportional : q α ∆T. The constant of proportionality between q and ∆T is called the heat capacity. Heat Capacity • Heat capacity (C) is the amount of heat (q) a substance must absorb to raise its temperature(∆T) by 1 °C. - Heat capacity has units of J/°C (or J/K), and is an extensive property, depending on the sample size. • Two type of heat capacity: 1) Heat capacity at constant volume: 2) Heat capacity at pressure constant Specific Heat • The specific heat (c, or specific heat capacity, Cs) of an object, is the quantity of heat required to change the temperature of 1 gram of a substance by 1 °C (or K): - Specific heat has units of J / g °C, and is an intensive property, which is independent of the sample size. • The molar heat capacity (Cm), is the quantity of heat required to change the temperature of 1 mole of a substance by 1 °C (or K): Heat Transactions In general the change in internal energy of a system: dwe is work in addition(e for “extra”) to the expansion work dwexp = 0, when a system kept a constant volume cannot do any expansion work. If the system also incapable of doing any other kind of work (if it is not, for instance, an electrochemical cell connected to an electric motor), then dwe = 0 too. Under these circumstances : Heat transfer at volume We express this relationship by writing, dU=dqv where the subscript implies a change at constant volume. For measurement change, A bomb Calorimeter The amount of heat absorbed by the water in the calorimeter is equal to the energy that is released by the reaction (but opposite in sign). qcal : heat absorbed by the entire calorimeter assembly Ccal: heat capacity of entire calorimeter assembly If no heat escape from the container: During the summer, you have experienced the effect of water’s high specific heat capacity. Example: Sacramento (an inland city) and San Francisco (a coastal city) can be 18oC (30oF). San Francisco enjoy cool 20oC (68oF) while Sacramento bakes at nearly 38oC (100oF). Why the large temperature difference? San Francisco sit on peninsula, surrounded by the Pacific Ocean. Water – absorbed much the sun’s heat without undergoing a large increase in temperature. While the Sacramento, with its low heat capacity undergoes a large increase in temperature as it absorbs a similar amount of heat. heat = mass x specific heat x temperature The high heat capacity of water surrounding San Francisco results in relatively cool summer temperatures. q= m x Cs x ∆T The specific heat can be used to quantify the relationship between the amount of heat added to a given amount of the substance and the corresponding temperature increase. The equation is: heat = mass x specific heat x temperature q= m x Cs x ∆T Example 2: Suppose you find a copper penny (minted pre-1982 when pennies were almost entirely were almost entirely copper) in the snow. How much heat is absorbed, by the penny as it warms, from the sun temperature of the snow, which is -8.0oC, to the temperature of your body, 37oC? Assume the penny is pure copper and has a mass of 3.10g. Sort: You are given the mass of copper as well as its initial and final temperature. You are asked to find the heat required for the given temperature change Given: m = 3.10 g copper Ti = -8.0 oC Tf = 37.0 oC Find : q Strategy: The equation q = m x Cs x ∆T Conceptual Plan: give the relationship between the Cs , m, ∆T → q amount of heat (q) and the temperature q = m x Cs x ∆T change (∆T ) Relationship Used: q = m x Cs x ∆T Cs = 0.385 J/g.oC Solve: Gather the necessary quantities for the equation in the correct units and Substitute these into the equation to compute q. Solution: ∆T = Tf – Ti = 37.0oC – (-8.0oC) = 45.0oC q = m x Cs x ∆T = 3.10 g x 0.385 J x 45.0oC = 53.7J g. oC Check : The unit (J) are correct for heat. The sign of q is positive, as it should be since the penny absorbed heat from surrounding. Energy Energy is define as the ability to do work. Work is done when a force is exerted through a distance. Force through distance; work is done. Energy is measured in Joules (J) or Calories (cal). 1 J = 1 kg m2 s-2 Energy may be converted from one to another, but it is neither created nor destroyed (conversion of energy). In generally, system tend to move from situations of high potential energy (less stable) to situations having lower energy (more stable). Unit of Energy • A calorie (cal) is the amount of energy needed to raise the temperature of 1 g of water by 1°C. 1 cal = 4.184 J • The nutritional unit Calorie (Cal) is actually a kilocalorie (kcal): 1 Cal = 1000 cal = 1 kCal = 4184 J Potential and Kinetic Energy • Kinetic energy (EK) is the energy due to the motion of an object with mass m and velocity v: EK = ½ mv2 – Thermal energy, the energy associated with the temperature of an object, is a form of kinetic energy, because it arises from the vibrations of the atoms and molecules within the object. • Potential energy (EP) is energy due to position, or any other form of “stored” energy. There are several forms of potential energy: – Gravitational potential energy – Mechanical potential energy – Chemical potential energy (stored in chemical bonds) Internal Energy •The internal energy, U of a system is the sum of the kinetic and potential energies of all the particles that compose the system or the total energy of a system. •Internal energy is the state function, which means that its value depends only the state of the system, not the how the system arrive at the state. •Some examples include energy (and many other thermodynamic terms), pressure, volume, altitude, distance, etc. • An energy change in a system can occur by many different combinations of heat (q) and work (w), but no matter what the combination, ΔU is always the same — the amount of the energy change does not depend on how the change takes place. ∆U = q + w Altitude is a state function. The change in altitude during climbing depends only on the difference between the final and initial altitudes. Example: reaction between carbon and oxygen to form carbon dioxide C(s) + O2 (g) CO2(g) In this reaction, energy is released from the system to the surroundings. – The reactants have a higher E than the products, so ΔU for the system is negative. – This energy is gained by the surroundings, where ΔU is positive. (ΔUsystem = -ΔUsurroundings) ΔU < 0 (negative) System ∆Usys < 0 (negative) Surroundings Energy flow ∆Usurr > 0 (positive) If the reaction is reversed, energy is absorbed by the system from the surroundings. – The reactants have a lower E than the products, so ΔU for the system is positive. – This energy is lost by the surroundings, where ΔU is negative. ΔU > 0 (positive) The difference , ∆U is positive and energy glows into the system and out of surroundings System ∆Usys > 0 (positive) Surroundings Energy flow ∆Usurr < 0 (negative) Summarizing: if the reactants have a higher internal energy than a products, ∆Usys is negative and energy flows out of the system into the surroundings. if the reactants have a lower internal energy than a products, ∆Usys is positive and energy flows into the system from the surroundings. A system can exchange energy with its surroundings through heat and work: Heat (q) System Surroundings Work (w) According to the first law thermodynamic, the change in the internal energy of the system (∆U) must be the sum of the heat transferred (q) and the work done (w): ∆U = q +w Sign of conventions for q, w, and ∆U q (heat) + system gain thermal energy - System loses thermal energy w (work) + work done on the system - Work done by the system ∆U + energy flows into the system (change in internal energy) - Energy flows out of the system • For an isolated system, with no energy flowing in or out of the system, the internal energy is a constant. – First Law of Thermodynamics (restated): The total internal energy of an isolated system is constant. • It is impossible to completely isolate a reaction from its surroundings, but it is possible to measure the change in the internal energy of the system, ΔU, as energy flows into the system from the surroundings or flows from the system into the surroundings. ∆U = Uf - Ui Enthalpy •Most reactions are not done in sealed containers: they are carried out in open vessels at constant pressure, with the volume capable of changing freely, especially if the reactants or products of the reaction involve gases. • In these cases, ΔV ≠ 0, and the energy change may be due to both heat transfer and PV work. • In order to eliminate the contribution from PV work, a quantity called enthalpy, H, is defined as internal energy (U) plus the product of pressure and volume: H = U + pV p: pressure, V:volume Because p,V,U are all state function, the enthalpy is a state function too. • The change in enthalpy (ΔH) is: ∆H = qP The Measurement of Enthalpy Change 1) Calorimeter Monitoring the temperature change that accompanies a physical or chemical change occurring at constant pressure. Example: thermally insulated vessel open to the atmosphere: the heat released in the reaction is monitor by measuring the change in temperature of the content. 2) Bomb Calorimeter Measuring the internal energy change. Hm = Um +pVm ≈ Um 3) Differential Scanning Calorimeter The most sophisticated way to measure enthalpy changes. Example 3: When 2.0 mol CO2 is heated at the constant pressure of 1.25 atm, it’s temperature increase from 250 K to 277K. Given the molar heat capacity of CO2 at constant pressure is 37.11JK-1, calculate q, ∆H and ∆U. Adiabatic Changes The change in internal change of a perfect gas when the temperature is change from Vi to Vf. Step 1: The volume changes and the temperature is constant at its initial value. The system expands at the constant temperature; there is no change in internal energy if the system consist of a perfect gas. Step 2: The temperature of the system is reduced at constant volume. Because the expansion is adiabatic, we know that q = 0; because ∆U=q + w , it then follows that ∆U = wad. Therefore, by equating the two expansion we have obtained for ∆U we obtained Wad = Cv ∆T Renungan: “Termodinamik merupakan satu subjek yang aneh. Kali pertama anda mempelajarinya, anda tidak faham langsung. Kali kedua anda mempelajarinya, anda fikir anda memahaminya kecuali satu dua perkara. Kali ketiga anda mempelajarinya, anda tahu bahawa anda tidak memahaminya, akan tetapi anda sudah terbiasa dengan subjek itu maka subjek itu tidak akan menjadi masalah lagi kepada anda” Arnorld Sommerfeld (1868-1951)