* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download chapter 2 properties of fluids
Hemorheology wikipedia , lookup
Coandă effect wikipedia , lookup
Accretion disk wikipedia , lookup
Airy wave theory wikipedia , lookup
Computational fluid dynamics wikipedia , lookup
Magnetohydrodynamics wikipedia , lookup
Navier–Stokes equations wikipedia , lookup
Aerodynamics wikipedia , lookup
Hydraulic machinery wikipedia , lookup
Reynolds number wikipedia , lookup
Derivation of the Navier–Stokes equations wikipedia , lookup
Bernoulli's principle wikipedia , lookup
Fluid thread breakup wikipedia , lookup
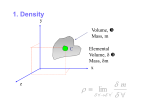
CHAPTER 2 PROPERTIES OF FLUIDS By Ummikalsom Abidin C24-316 FKM, UTM SME 1313 Fluid Mechanics I Introduction Property – any characteristic of a system Intensive properties Properties that are independent of the mass of a system e.g temperature, pressure, density Extensive properties E.g pressure P, temperature T, volume V, and mass m Properties whose values depend on size-or-extent-of the system e.g mass, total volume, total momentum Specific properties Extensive properties per unit mass e.g specific volume (v=V/m) and specific total energy (e=E/m) SME 1313 Fluid Mechanics I Introduction m V T P ρ ½m ½m ½V ½V T T P P ρ ρ Criteria to differentiate intensive and extensive properties SME 1313 Fluid Mechanics I Extensive properties Intensive properties Introduction State postulate – the state of a simple compressible system is completely specified by two independent, intensive properties SME 1313 Fluid Mechanics I Continuum Concept of a Fluid The number of molecules involved is immense, and the separation between them is normally negligible by comparison with the distances involved in the practical situation being studied Although the properties of a fluid arise from its molecular structure,engineering problem are usually concerned with the bulk behavior of fluids Under these conditions, it is usual to consider a fluid as a continuum - a hypothetical continuous substance – and the conditions at a point as the average of a very large number of molecules surrounding that point within a distance which is large compared with the mean intermolecular distance SME 1313 Fluid Mechanics I Density Density is defined as mass per unit volume ρ=m (kg/m3) V Specific volume is defined as volume per unit mass v = V = 1 (m3/kg) m ρ Density of a substance, in general depends on temperature and pressure SME 1313 Fluid Mechanics I Specific Gravity Specific gravity or relative density is defined as the ratio of the density of a substance to the density of some standard substance at a specified temperature (usually water at 4oC, for which ρH O=1000 kg/m3) SG = ρ ρH2O 2 Specific gravity is a dimensionless quantity SME 1313 Fluid Mechanics I Specific Gravity Substance SG Water 1.0 Blood 1.05 Seawater 1.025 Gasoline 0.7 Ethyl Alcohol 0.79 Mercury 13.6 Wood 0.3-0.9 Gold 19.2 Bones 1.7-2.0 Ice 0.92 Air (at 1 atm) 0.0013 Specific gravities of some substances at 0oC SME 1313 Fluid Mechanics I Specific Weight Specific weight is the weight of a unit volume of a substance γs= ρg (N/m3) Where, g = gravitational acceleration, 9.81 m/s2 SME 1313 Fluid Mechanics I Density of Ideal Gas Ideal gas equation Pv = RT or P = ρRT Where, P = absolute pressure v = specific volume T = thermodynamic (absolute temperature) T(K) = T(oC) + 273.15 ρ = gas density R = gas constant SME 1313 Fluid Mechanics I Vapor Pressure and Cavitation Saturation temperature, Tsat – the temperature at which a pure substance changes phase at a given pressure Saturation pressure, Psat – the pressure at which a pure substance changes phase at a given temperature Vapor pressure, Pv of a pure substance – the pressure exerted by its vapor in phase equilibrium with its liquid at a given temperature Partial pressure – the pressure of a gas or vapor in a mixture with other gases SME 1313 Fluid Mechanics I Vapor Pressure and Cavitation Possibility of the liquid pressure in liquid-flow system dropping below the vapor pressure at some location, and resulting unplanned vaporization A fluid vaporizes when its pressure gets too low, or its temperature too high. All centrifugal pumps have a required head (pressure) at the suction side of the pump to prevent this vaporization. Suction cavitation occurs when the pump suction is under a low pressure/high vacuum condition where the liquid turns into a vapor at the eye of the pump impeller. Cavitation must be avoided in flow systems since it reduces performance, generates vibration and noise and causes damage to the equipment SME 1313 Fluid Mechanics I Energy and Specific Heat Energy – mechanical, thermal, kinetic, potential, electric, etc. Microscopic energy – the forms of energy related to the molecular structure of a system and the degree of the molecular activity Internal energy, U – sum of all microscopic forms of energy Macroscopic energy – energy related to motion and the influence of some external effects such as gravity, magnetism, electricity, surface tension E.g potential energy, kinetic energy SME 1313 Fluid Mechanics I Energy and Specific Heat Enthalpy, h h = u + Pv = u + P ρ Where, P = flow energy, energy per unit mass needed to ρ move the fluid and maintain flow SME 1313 Fluid Mechanics I Energy and Specific Heat For ideal gas, the internal energy and enthalpy can be expressed in terms of specific heat ∆u = cv,ave ∆T and ∆h = cp,ave ∆T Where, cv,ave = average specific heat at constant volume cp,ave = average specific heat at constant pressure For incompressible substance, ∆h = ∆u + ∆ P/ρ ≅ cave ∆T + ∆ P/ρ SME 1313 Fluid Mechanics I Coefficient of Compressibility Coefficient of compressibility κ (also called the bulk modulus of compressibility or bulk modulus of elasticity) for fluids as (Pa) κ = - v ∂P = ρ ∂P ∂ρ T ∂V T In term of finite changes κ ≅ - ∆P ≅ ∆P (T=constant) ∆v/v ∆ρ/ρ Large κ, a large change in pressure is needed to cause a small fractional change in volume (incompressible e.g liquids) SME 1313 Fluid Mechanics I Coefficient of Compressibility For an ideal gas, P = ρRT and (∂P/ ∂ρ)T = RT = P/ρ And thus, (Pa) κideal gas = P Coefficient of compressibility of an ideal gas is equal to its absolute pressure and it increases with increasing pressure Substituting κ = P into definition of the coefficient of compressibility and rearranging gives ∆ρ = ∆P (T=constant) ρ P The percent increase of density of an ideal gas during isothermal compression is equal to the percent increase in pressure SME 1313 Fluid Mechanics I Isothermal Compressibility Isothermal compressibility is the inverse of the coefficient of compressibility α = 1 = - 1 ∂V = 1 ∂ρ (1/Pa) κ v ∂P T ρ ∂P T Isothermal compressibility of fluid represents the fractional change in volume or density corresponding to a unit change in pressure SME 1313 Fluid Mechanics I Coefficient of Volume Expansion Coefficient of volume expansion provide information on variation of density of a fluid with temperature at constant pressure = - 1 ∂ρ (1/K) β = 1 ∂v ρ ∂T P v ∂T P In term of finite changes β ≅ ∆v/v ≅ - ∆ρ/ρ (P=constant) ∆T ∆T Large β for a fluid means a large density change in density with temperature SME 1313 Fluid Mechanics I Coefficient of Volume Expansion (∂v/∂T)P (∂v/∂T)P 20oC 100 kPa 1 kg 21oC 100 kPa 1 kg (a) Substance with a large β 20oC 100 kPa 1 kg 21oC 100 kPa 1 kg (b) Substance with a small β The coefficient of volume expansion is a measure of the change in volume of a substance with temperature at constant pressure SME 1313 Fluid Mechanics I Coefficient of Volume Expansion For ideal gas, the volume expansion coefficient at a temperature T is βideal gas = 1 (1/K) T Where, T=absolute temperature SME 1313 Fluid Mechanics I Coefficient of Volume Expansion The combined effects of pressure and temperature changes on volume change of a fluid can be determined by taking the specific volume to be a function of T and P Differentiating v=v(T,P) and using the definitions of compression and expansion coefficient α and β give dv = ∂v dT + ∂v dP =(β dT – α dP) v ∂T P ∂P P The fractional change in volume (or density) due to changes in pressure and temperature can be expressed approximately as ∆v = - ∆ρ ≅ β∆T - α∆P v ρ SME 1313 Fluid Mechanics I Problem 2-32 Problem 2-32 Water at 1 atm pressure is compressed to 800 atm pressure isothermally. Determine the increase in the density of water.Take the isothermal compressibility of water to be 4.80 x 10-5 atm-1 SME 1313 Fluid Mechanics I Example 2-3 Example 2-3 Consider water initially at 20oC and 1 atm. Determine the final density of water (a) if it is heated to 50oC at a constant pressure of 1 atm, and (b) if it is compressed to 100-atm pressure at constant temperature of 20oC. Take the isothermal compressibility of water to be α=4.80x10-5 atm-1 SME 1313 Fluid Mechanics I Viscosity Viscosity is a property that represents the internal resistance of a fluid to motion or the ‘fluidity’ Consider a fluid layer between two very large parallel plates separated by distance l dA N Area A N’ Force F u=V Velocity V dβ l y Velocity profile M u=0 u(y)=(y/l)V x Behavior of a fluid in a laminar flow between two parallel plates when the upper plate moves with a constant velocity SME 1313 Fluid Mechanics I Viscosity A constant parallel force F is applied to the upper plate, the lower plate is held fixed The upper plate moves continuously at constant velocity under the influence of F The shear stress τ acting on the fluid layer is F τ= A Where, A=contact area between the plate and the fluid SME 1313 Fluid Mechanics I Viscosity Fluid in contact with lower plate has zero velocity (no-slip condition) In steady laminar flow, the fluid velocity between the plates varies linearly between 0 and V, and thus the velocity profile and the velocity gradient are y u( y) = V l and du V = dy l Where, y=vertical distance from lower plate SME 1313 Fluid Mechanics I Viscosity The angular displacement or deformation (or shear strain) can be expressed as dβ ≈ tan β = da dt du dt =V = l l dy Rearranging, the rate of deformation dβ du = dt dy SME 1313 Fluid Mechanics I Viscosity The rate of deformation of a fluid element is equivalent to the velocity gradient du/dy Fluids rate of deformation (and thus the velocity gradient) is directly to the shear stress τ dβ τ∝ dt or du τ∝ dy Newtonian fluids for fluids which its rate of deformation is proportional to the shear stress SME 1313 Fluid Mechanics I Viscosity In 1-D shear flow of Newtonian fluids, shear stress can be expressed by linear relationship du τ = µ dy Where, µ=coefficient of viscosity/dynamic(absolute) viscosity of the fluid, N.s/m2 (or Pa.s) Poise=0.1 Pa.s SME 1313 Fluid Mechanics I Viscosity The shear force acting on a Newtonian fluid layer is du F = τA = µA dy (N) The force F required to move the upper plate at constant velocity of V while the lower plate remains stationary is F = µA V l (N) SME 1313 Fluid Mechanics I Viscosity Kinematic viscosity is the ratio of dynamic viscosity to density µ (m2/s) υ = ρ SME 1313 Fluid Mechanics I Viscosity Oil Viscosity=slope Shear stress, τ µ= a b τ a = du dy b Water Air Rate of deformation, du/dy The rate of deformation (velocity gradient) of a Newtonian fluid is proportional to shear stress, and the constant of proportionality is the viscous SME 1313 Fluid Mechanics I Viscosity Bingham plastic Shear stress, τ Pseudoplastic Newtonian Dilatant Rate of deformation, du/dy Variation of shear stress with the rate of deformation for Newtonian and nonNewtonian fluids (the slope of a curve at a point is the apparent viscosity of the fluid at that point) SME 1313 Fluid Mechanics I Viscosity Viscosity is due to the internal frictional force that develops between different layers of fluids as they are forced to move relative to each other Gases Viscosity is caused by molecular collisions Viscosity of gas increases with temperature In a gas, molecular forces are negligible and the gas molecules at high temperatures move randomly at higher velocities This results in more molecular collisions per unit volume per unit time, thus greater resistance to flow SME 1313 Fluid Mechanics I Viscosity of Gas Viscosity of gases is expressed as function by the Sutherland correlation aT 1 / 2 µ= 1+ b T Where, T=absolute temperature (K) a and b = experimentally determined constants SME 1313 Fluid Mechanics I Viscosity of Liquid Liquids Viscosity is due to the cohesive forces between the molecules At higher temperatures, molecules posses more energy, and they can oppose the large cohesive intermolecular forces more strongly The liquid viscosity is approximated as µ = a10 b /(T −c ) Where, T=absolute temperature (K) a, b and c = experimentally determined constants SME 1313 Fluid Mechanics I Viscosity of Gas and Liquid Viscosity Liquids Gases Temperature The viscosity of liquids decreases and the viscosity of gases increases with temperature SME 1313 Fluid Mechanics I Example 2-4 Determining the Viscosity of a Fluid The viscosity of a fluid is to be measured by viscometer constructed of two 40-cm-long concentric cylinders (Fig. 218).the outer diameter of the inner cylinder is 12 cm, and the gap between the two cylinders is 0.15 cm. The inner cylinder is rotated at 300 rpm, and the torque is measured to be 1.8 N.m. Determine the viscosity of the fluid SOLUTION The torque and the rpm of a double cylinder viscometer are given. The viscosity of the fluid is to be determined Assumptions 1) The inner cylinder is completely submerged in oil 2) The viscous effects on the two ends of the inner cylinder are negligible Analysis The velocity profile is linear only when the curvature effects are negligible, and the profile can be approximated as being linear in this case since l/R<<1 SME 1313 Fluid Mechanics I Example 2-4 Determining the Viscosity of a Fluid Stationary cylinder R N=300 rpm Shaft l Fluid Figure 2-18 SME 1313 Fluid Mechanics I Surface Tension Liquid droplets behave like small spherical balloons filled with the liquid, and the surface of the liquid acts like a stretched elastic membrane under tension. The pulling forces that causes this tensions acts parallel to the surface and is due to the attractive forces between the molecules of the liquid. A molecule on the surface A molecule inside the liquid Attractive forces acting on a liquid molecule at the surface and deep inside the liquid SME 1313 Fluid Mechanics I Surface Tension The magnitude of the force per unit length is called surface tension, σs (N/m) SME 1313 Fluid Mechanics I Capillary Effect Capillary effect is the rise or fall of a liquid in a smalldiameter tube inserted into liquid Capillaries is a narrow tubes or confined flow channels The curved free surface of a liquid in a capillary tube is called meniscus Φ Φ a) Wetting fluid b) Nonwetting fluid SME 1313 Fluid Mechanics I Capillary Effect Contact (or wetting) angle Φ, is defined as the angle that the tangent to the liquid surface makes with the solid surface at the point of contact Φ<90o Φ>90o The liquid is to wet the surface The liquid is not to wet the surface Cohesive forces is forces between like molecules (water-water), adhesive forces is forces between unlike molecules (water-glass). Water molecules are more strongly attracted to the glass molecules than they are to other water molecules, and thus water tends to rise along the glass surface SME 1313 Fluid Mechanics I