Download Quantum Monte-Carlo for Non

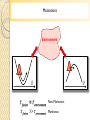
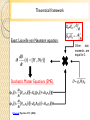
Quantum Monte-Carlo for Non-Markovian
Dynamics
Guillaume Hupin
GANIL, Caen FRANCE
Collaborator
: Denis Lacroix
Overview
1. Motivation in nuclear physics : Fission and Fusion.
2. Non-Markovian effects : Projective methods.
3. Quantum Monte-Carlo.
System
Environment
4. Applications :
A. To the spin-star model.
B. To the spin-boson model.
C. In the Caldeira Leggett model.
Physics case : fission
H. Goutte, J. F. Berger,
P. Casoli, Phys. Rev. C
71 (2005)
Environment
 Nucleons
System:
and
potential
Environment: Nucleons
(intrinsic) motion
Coupling:
response
thermal bath.
 Fast
motion
fission decay.
—› Markovian
vs
Physical case : fusion
Different channels are opened
in a fusion reaction :
Relative distance.
Environment
System : relative distance.
Environment : nucleon motion,
other degrees of freedom
(deformation…).
=> Non-Markovian effects are
expected.
Microscopic evolution can be
mapped to an open quantum
system.
K.Washiyama et al., Phys. Rev. C 79, (2009)
Motivations
Environment
Q
Q
Non-Markovian.
Markovian.
Framework
The total Hamiltonian written as
 (S) is the system of interest
coupled to (E).
 (E) is considered as a general
environment.
Exact Liouville
equation.
von
Neumann
The environment has too
many degrees of freedom.
Standard approaches : projective methods
Exact evolution
System
System only
evolution
I = interaction
picture
Therefore, use projective methods to “get rid” of (E).
First, define two projection operators on (S) and (E).
Project the Liouville equation on the two subspace.
System
Environment
Standard approaches : projective methods
The equation of motion of
the system is closed up to a
given order in interaction.
H. Breuer and F. Petruccione, The Theory of Open
Quantum Systems (Oxford University Press,
Oxford, 2002)
Nakajima-Zwanzig’s method (NZ).
s
t
Time non local method : mixes
order of perturbation. (NZ2,
NZ4..)
Time Convolution Less method (TCL).
s
t
Time local method : order of the
perturbation under control.
(TCL2,TCL4 …)
Comparison between projective techniques
In the CaldeiraLeggett model: an
harmonic oscillator
coupled to a heat
bath.
Q
Using a Drude
spectral density:
Exact
NZ2
NZ4
Exact
TCL2 (perturbation)
TCL4
TCL4 is in any case a
more accurate method.
G.Hupin and D. Lacroix, Phys. Rev. C 81, (2010)
New approach : Quantum Monte Carlo
The exact dynamics is replaced
by a number of stochastic paths
to simulate the exact evolution
in average.
D is complicated : The
environment has too many
degrees of freedom.
 Noise designed to account for
the coupling.
t0
t
Theoretical framework
Exact Liouville von Neumann equation.
Other
stat.
moments are
equal to 0.
Stochastic Master Equations (SME).
D. Lacroix, Phys. Rev. E 77, (2008)
Theoretical framework : proof
SME Proof :
Using our Stochastic
Master Equations.
SME has its equivalent Stochastic Schrödinger Equation
Deterministic evolution
Stochastic Schrödinger equation (SSE):
…
Leads to the equivalence :
L.Diosi and W.T. Strunz Phys. Lett. A 255
(1997)
M.B. Plenio and P.L. Knight, Rev. Mod. Phys.
70 (1998)
J.Piilo et al., PRL 100 (2008)
A. Bassi and L. Ferialdi PRL 103 (2009),
Among many others…..
Independence of the
statistical moments :
Application of the SSE to spin star model
Statistical fluctuation :
A Monte-Carlo simulation
is exact only when the
statistical convergence is
reached.
1000
Trajectories
Noise optimized.
Including the mean field solution
Take the
separable :
density
as
Then, take the Ehrenfest
evolution :
Position & momentum : ok
Width : not ok
Mean field + QMC
D. Lacroix, Phys. Rev. A 72, (2005)
Evolution of the statistical
fluctuation have been
reduced
using
an
optimized deterministic
part in the SME.
Projected Quantum Monte-Carlo + Mean-Field
Exact evolution
The environment response
is contained in :
System
Stochastic
trajectories
Link with the Feynman path integral formalism
J.T. Stockburger and H. Grabert, Phys. Rev. Lett. 88, (2002)
Application to the spin boson model
This method has been applied to spin boson
model.
Exact (stochastic)
TCL2
A two level system
interacting with a
boson bath
Second successful
test.
D. Lacroix, Phys. Rev. E 77,
(2008)
Y. Zhou , Y. Yan and J. Shao,
EPL 72 (2005)
Application to the problems of interest
Environment
Fission/fusion processes
The potential is first locally approximated by
parabola.
Benchmark in the Caldeira-Leggett model
Second moment
evolution.
Q
 QMC.
 Exact.
Convergence is achieved
 for second moments for different temperatures.
 with an acceptable time of calculation.
 with a limited number of trajectories (≈104 ).
Observables of interest
E
Exact.
Quantum Monte Carlo.
Projection 2nd order in interaction.
Projection 4nd order in interaction.
Passing probability
2nd order in
perturbation TCL
Markovian
approximation
E
Monte Carlo
Accuracy of MC simulations
is comparable to the fourth
order of projection.
4th
order in
perturbation TCL
 Accuracy of such calculations
Exact
are of interest for very heavy
nuclei.
Summary
It has been pointed out that TCL4 should be preferred.
New theory based on Monte Carlo technique has been applied and
tested for simple potentials.
This study shows that the new method is effective.
Now, the new technique Monte-Carlo+Mean-Field should be applied
to more general potentials.
Critical issue: diverging path
Possible solutions :
C. Gardiner, “A Handbook of Stochastic
 Remove the diverging trajectories. Methods”
Semi-classic approximations : Initial Value Methods
W. Koch et al. , PRL 100 (2008)