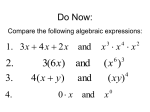Download 6.2 EXPONENTS

6.2 EXPONENTS
Emily is taking an astronomy course and read the following in her textbook:
The circumference of the Earth (the distance around the equator) is approximately 2.49 × 104 miles.
Emily has seen scientific notation before, but only knows that it is a way to
represent very large or very small numbers without writing out all the place
digits. But now that she has learned about exponents, she realizes that this
number is actually just a problem to be solved. She’s pretty sure she even
knows how to solve it! Her goal is to write out the number, showing all the
place values, so she can see how many miles it is.
She knows that she must first calculate the value of 104.
Then she will multiply that value by 2.49. Can you do it?
10,000 × 2.49 = ______________
24,900 miles
104 = ____________
Assess your readiness to complete this activity. Rate how well you understand:
Not
ready
Almost
ready
Bring
it on!
• the terminology and notation associated with exponents
• how to write expressions in exponential notation
• how to evaluate exponential expressions
• how to order a mixed set of numbers and numerical expressions
•
Writing expressions in exponent form
– correct notation
•
Evaluating expressions with exponents
– accuracy
•
Ordering a set of numbers and numerical
expressions
– accurate conversions to the same form
– correct order
257
Chapter 6 — Signed Numbers, Exponents, and Order of Operations
Technique
To evaluate an exponential expression is to simplify the expression to a single number. The
most accurate way to do this is to write out the factors of the expression and then multiply
them.
Model 1
Evaluate each of the following:
(0.06)2
(0.06)2 = 0.06 × 0.06 = 0.0036 Answer
0.06
×0.06
0.0036
(–3)5
(–3)5 = −3 × (–3) × (–3) × (–3) × (–3)
=
=
+9
× (–3) × (–3) × (–3)
−27
=
× (–3) × (–3)
+81
=
× (–3)
− 243
Answer: –243
2
⎛ 2 ⎞⎟
⎜⎜ ⎟
⎝⎜ 5 ⎟⎠
2
⎛ 2 ⎞⎟
⎜⎜ ⎟ = 2 × 2 = 4 Answer
⎝⎜ 5 ⎟⎠
5 5 25
102 + 24
Evaluate each term separately:
102 = 10 × 10 = 100
24 = 2 × 2 × 2 × 2 = 16
102 + 24 = 100 + 16 = 116 Answer
258
OR
Use the shortcut for multiplying
more than two signed numbers. With
five negative factors, the answer will
be negative. Multiply 3×3×3×3×3
and attach a negative sign:
Activity 6.2 — Exponents
Evaluate (−4)2 and −42.
There is an important distinction to be made between (–4)2 and –42.
(−4)2
Because of the parentheses around the −4, the term (–4)2 represents
the base number –4 raised to the second power:
(−4) × (−4) = +16
That is, (−4)2 = +16 Answer
−42
On the other hand, the negative sign in the expression –42, indicates
“the opposite of” the base number 4 raised to the second power:
–42 = the opposite of 42
= the opposite of 4 × 4 or the opposite of 16
That is, –42 = –16 Answer
Evaluate (−4)3 and −43.
Note that, with an odd power, both simplified answers are the same.
(−4)3 = (−4) × (−4) × (−4) = −64 Answer
−43 = the opposite of 4 × 4 × 4, or the opposite of 64, or −64 Answer
Model 2
Combine your knowledge of signed numbers and exponents, and list the following sets of numerical
expressions in order from lowest to highest value.
–2, –42, 12, –10, (–5)2
Original list: –2, –42, 12, –10, (–5)2
Evaluate the expressions
with exponents:
–42 = −(4 × 4) = −16
(–5)2 = (–5) × (–5) = +25
List after evaluating
terms with exponents:
–2, –16, 12, –10,
25
Visualize on a number line (optional).
–16 –10
12
–2
25
–16 < –10 < –2 < 12 < 25
That is, from lowest to highest:
–42, –10, –2, 12, (–5)2
Answer
259
Chapter 6 — Signed Numbers, Exponents, and Order of Operations
32 , −
1
, 0,
2
2
(2.1)
, − 4.2
Original list: 32 , −
Evaluate the expressions
with exponents:
1
, 0,
2
2
(2.1)
, − 4.2
32 = 3 × 3 = 9
(2.1)2 = 2.1 × 2.1 = 4.41
List after evaluating
terms with exponents: 9,
1
, 0, 4.41, − 4.2
2
9, − 0.5, 0, 4.41, − 4.2
Since two are decimals, compare as decimals.
Visualize on a number line (optional).
−
–4.2 –0.5 0
4.41
9
–4.2 < –0.5 < 0 < 4.41 < 9
Using the original numbers,
the list from lowest to highest is:
Make Your Own Model
1
2
2
2
– 4.2, – , 0, (2.1) , 3 Answer
Either individually or as a team exercise, create a model demonstrating
how to solve the most difficult problem you can think of.
Answers will vary.
Problem: _________________________________________________________________________
260
Activity 6.2 — Exponents
1. What is the meaning of an exponent? Provide an example and explain.
In the problem 43= ?
The 3 is the exponent and the 4 is the base. The exponent tells you how many times to use the base as a factor to
evaluate the expression. In this problem you would evaluate 4 × 4 × 4.
2. What kind of number(s) can you use for the base?
Any number can be used as the base. It can be a whole number, a fraction, or a decimal and it can be either positive
or negative.
3. What does it mean to have an exponent of one (1)?
Use the base number as a factor only one time. In other words, the base is the answer to the problem where the
exponent is one.
4. What is the value of one (1) raised to any power?
One raised to any power is 1.
5. What is the result when you evaluate a negative number raised to an even number exponent?
Raising a negative number to an even number exponent is the same as multiplying an even number of negative
numbers together, so the result will be positive.
6. What is the result when you evaluate a negative number raised to an odd number exponent?
Raising a negative number to an odd number exponent is the same as multiplying an odd number of negative
numbers together, so the result will be negative.
7. How can you represent a number added to itself four times versus a number multiplied by itself four
times?
A number x added to itself four times is x + x + x + x = 4x. But x • x • x • x = x4
8. What aspect of the model you created is the most difficult to explain to someone else? Explain why.
Answers will vary.
261
Chapter 6 — Signed Numbers, Exponents, and Order of Operations
1. Write each expression in exponent form and then evaluate it.
Exponent Form
Expression
Evaluation
a) 7 × 7 × 3 × 3 × 3
b) 2 • 2 • 2 • 2 • 5 • 5 • 11
c) 3 × 3 + 5 × 5 × 5
2. Evaluate the following exponential expressions:
a) 43 × 22 × 30
3
⎛1 ⎞
b) ⎜⎜⎜ ⎟⎟⎟
⎝5 ⎠
262
43 = 4 • 4 • 4 = 64
64 ×4 = 256
22 = 4
30 = 1
256 ×1 = 256
1 1 1
1
× × =
5 5 5
125
Answer
Answer
Activity 6.2 — Exponents
2
⎛ 2⎞
c) ⎜⎜⎜− ⎟⎟⎟
−
⎝ 3⎠
d) –112
Answer
–11 • 11 = –121
e) 52 + 103
f) (0.03)3
2
2
4
×− =
3
3
9
Answer
52= 25
25 + 1000 = 1025
3
10 = 10 • 10 • 10 = 1,000
= 0.03 × 0.03 × 0.03
= 0.0009 × 0.03 = 0.000027
g) 157
Answer
= 1
Answer
Answer
3. Which is greater? 53 or 35
4. What number is 1 less than 103?
53 = 5 × 5 × 5 =125
35 = 3 × 3 × 3 × 3 × 3
=
9 ×
9 ×3
=
81 × 3 = 243
243 > 125
35 > 53
Answer: 35 is greater
103= 10 • 10 • 10 = 100 • 10 = 1,000
1,000 – 1 = 999 Answer
1
, − 52 , 12, − 10,
8
5. Order the following from lowest to highest value:
2
(−5)
1
2
, − 52 , 12, − 10, (−5)
8
+25
–25
3
1
4
2
–52, –10, 1 , 12, (–5)2
8
5
Answer
263
Chapter 6 — Signed Numbers, Exponents, and Order of Operations
Evaluate each of the following expressions.
1. Write in exponential notation:
2
3. Evaluate:
9 •2
a) 9 • 9 • 2 • 2 • 2
3
b) 10 × 6 × 6 × 6 × 6 × 3 × 3
10 × 64 × 32
(order could be different)
2. Order the following from lowest to highest value:
2 , –4 , –2 , (–4) , –2
3
2
3
2
5
5
2
3
3
343
(–6)2 36
(0.5)3 0.125
82 + 8 72
402 1,600
4.41
(–9)3 –729
(–1)15 –1
3
⎛ 2 ⎞⎟
8
⎜⎜ ⎟
⎜⎝ 5 ⎟⎠ 125
a) 73
f) (2.1)2
b)
c)
g)
d)
e)
2
–2 , –4 , –2 , 2 , (–4)
h)
i)
Identify the error(s) in the following worked solutions. If the worked solution is correct, write “Correct” in the
second column. If the worked solution is incorrect, solve the problem correctly in the third column.
Worked Solution
What is Wrong Here?
1) Evaluate: 62 • 25
Identify the Errors
Used the exponent as a factor.
2
6 means 6 × 6,
not 2 × 6.
25 means 2 × 2 × 2 × 2 × 2,
not 5 × 2
2
⎛1 ⎞
2) Evaluate: ⎜⎜ ⎟⎟⎟
⎜⎝ 4 ⎠
Multiply across, do not add
the numerators.
3) Evaluate: (–0.02)3
There are six decimal places
needed in the product.
264
Correct Process
62 × 25
=6×6×2×2×2×2×2
4
= 36 ×
= 1152
×
32
4
×2
36
× 32
72
1080
1 1 52