Download Geometry Fall 2011 Lesson 17 (S.A.S. Postulate)

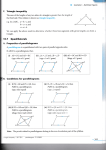
1
Lesson Plan #53
Date: Thursday January 19th, 2017
Class: Geometry
Topic: Rhombus
Aim: What are some properties of rhombi?
Objectives:
1) Students will know the properties of a rhombus.
2) Students will be able to use the properties of a rhombus.
3) Students will be able to prove that a quadrilateral is a rhombus.
HW #53:
Do Now:
1) Identify the figure at right.
2) What is the definition of the figure at right?
As a result, it has all the properties of a parallelogram such as
 Opposite sides parallel
 Opposite sides congruent
 A diagonal divides it into two congruent triangles
 Opposite angles are congruent
 Consecutive angles are supplementary
 The diagonals bisect each other.
What 3 other properties do you notice in this figure?
1.
2.
3.
PROCEDURE:
Write the Aim and Do Now
Get students working!
Take attendance
Give Back HW
Collect HW
Go over the Do Now
Assignment #1: Let’s see how we can construct a rhombus.
http://www.glencoe.com/sites/texas/student/mathematics/assets/animation/ge
ometry/GEOMCIM6-5.swf
Properties of a Rhombus:
1) A rhombus has all the properties of a parallelogram
2) A rhombus is equilateral
3) The diagonals of a rhombus are perpendicular to each other
4) The diagonals of a rhombus bisect its angles.
Methods to prove a quadrilateral is a rhombus:
1) The quadrilateral is a parallelogram with two congruent consecutive sides.
2) The quadrilateral is equilateral.
3) The quadrilateral is a parallelogram whose diagonals are perpendicular to each other.
4) The quadrilateral is a parallelogram, and a diagonal bisects the angles whose vertices it joins.
2
Online Interactive Activity : Let’s go to http://www.mathopenref.com/rhombus.html and see how we can make
different rhombi, but they all still have the properties of a rhombus.
Online Interactive Activity : Let’s go the math warehouse and practice using the properties of a rhombus
http://www.mathwarehouse.com/geometry/quadrilaterals/parallelograms/rhombus.php
Examples:
Sample Test Questions:
1)
2)
3)
4)
3
On Your Own:
12) In rhombus ABOL shown at right, diagonal BL is drawn, H and S are points
LO , respectively, and HS intersects BL at I.
o
o
If m  A  122 , and m  HIB  18 , find m  ISO .
on AB and
4
If enough time:
1)
2)
3)
4)
5)
5
6)
7)
6
8)