* Your assessment is very important for improving the work of artificial intelligence, which forms the content of this project
Download 5.1 Homework Quiz
Survey
Document related concepts
Transcript
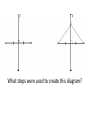
5.1 Homework Quiz 1. What are the 4 ways of knowing that we discussed last time in class? 2. Find the measure of the missing angle in the diagram below assuming the figure is made up of 2 lines: 108 ? 1. What are the minimal conditions necessary to identify that two triangles are congruent (one is just a transformation of the other)? Or in other words, what are the triangle congruence theorems? Do you See What I See Last time we looked at the figure below and imagined how it was constructed and then I showed you how it was constructed. The final diagram we said suggested that the sum of the angles of a triangle is 180 degrees. What can you say about the triangle in the following diagram? What convinces you that you can make this claim? Did you make any assumptions with this claim? List several conjectures that you believe are true about the triangles, quadrilateral, and diagonals of the quadrilateral in the figure below. What have we proven/accept as axioms? Properties of the transformations: rotation, reflection, translation Any angles that together create a straight line, sum to 180 degrees. Triangle congruence theorems Pythagorean Theorem Conjectures to be Proven 1. The base angles of isosceles triangles are congruent 1. The diagonals of a rhombus bisect each other 1. The diagonals of a rhombus are perpendicular *Trick: Prove different triangles are congruent. What steps were used to create this diagram? Hannah and Abi were doing their math homework together. One of the questions asks them to prove the following statement. The points on the perpendicular bisector of a segment are equidistant from the endpoints of the segment. They thought this diagram would be helpful for justification along with descriptions. Given information Just need to pick an arbitrary point C on l. Restating goal Construct line segments AC and BC to create triangles. Thinking. Not necessary for the argument It might be easier to order these statements by talking about the angle measure in between the two sides. We need to name the two triangles that are congruent A and B are equidistant from C What have we proven: -Properties of the transformations -Any angles that create a straight line total 180 degrees. -Triangle congruence theorems -Pythagorean Theorem *The base angles of isosceles triangles are congruent. *The diagonals of a rhombus bisect each other. *The diagonals of a rhombus are perpendicular. *The points on the perpendicular bisector of a segment are equidistant from the endpoints of the segment.