Download Equipment: Rulers, meter sticks, string, tennis balls, transparent tape

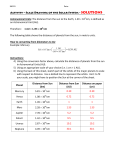
Equipment: Rulers, meter sticks, string, tennis balls, transparent tape, paper, compasses,
calculators, assorted planets.
Introduction: This lab is divided into three parts. In the first part you will draw the nine planets to scale
in order to get some idea as the relative sizes of things. In the second part you will draw the orbits of the
planets to scale so you will get an idea as to the relative distances between the planets and their order
from the sun. In the third part you will go outside and make both the sizes of the planets and their orbits
to the same scale so you can get an overall view of the solar system.
Below is the data that you will use. The distances to the Sun are given in A.U. (Astronomical Units),
which is the average distance between the Earth and the Sun (the earth is the black circle in the upper
right of the first cell of the data able). 1 A.U. is about 1.5 x 108 km (~93 Million miles). The diameters of
the planets are given in terms of Earth's diameter. The average diameter of the earth is about 12,756 km
(~8000 miles). We will abbreviate the Earth's diameter as ED
Data Table
Example – The actual diameter Neptune is
49,528 km. The diameter of the earth is
12,756 km – so the diameter of Neptune is
3.88 times greater than the diameter of the
earth.
Part One: Drawing the sizes of the planets to scale
Note: In this section we ignore the orbits of the planets and concentrate on their size. Disregard the
A.U. distances in this part.
Let the Earth's diameter be set equal to one centimeter. Drawn to this scale, Neptune would be about 3.8
cm in diameter, or 1.9 cm in radius.
Tape two pieces of paper together and draw a light, thin line through the middle. See the figure below.
Use a compass, or in the case of the smaller planets freehand, to draw the planets. Remember, if you use a
compass that you should measure the radius on the ruler, not the diameter. The Sun is so large you will
need to use a piece of string as a compass to sketch its shape. It will not fit on the paper. Place the planets
close together so that they will fit on the paper. Label each planet.
Part Two: Drawing the orbits of the planets to scale.
Note: In this section we consider the size of the orbits, on this scale the size of the planets would be
smaller than your pencil point. Do not draw the planets for this part of the lab.
On the other side of your taped paper draw the orbits of the planets to a scale of I cm (centimeter) to 1
A.U. You will be able to use a compass for some of the inner planets but you will need to use string on
some of the outer ones. Note: The distances to the Sun is the radius of the orbit, not the diameter. Start
with a dot representing the Sun located about 10 cm (centimeters) from the left edge. Some orbits are too
large to fit entirely on the paper. Label each orbit. See figure.
Part Three: Putting it all together.
Now we will build a solar system where every thing is at the same scale. In this scale the Sun will be the
size of a tennis ball and the sizes of the planets and the sizes of the orbits will be calculated accordingly.
For this exercise, you will work in groups of 6-9 students, each responsible for 1planet or up to 3 inner
planets. If one team member is doing multiple planets (fewer than 9 team members), they should be
Mercury, Venus and Earth, in that order, if they have 1,2 or 3 planets, respectively.
Using the size of the Sun, the data table and the diameter of the tennis ball, calculate the diameter for the
model planet. (example: the Earth model object should be 1/108 the diameter of the tennis ball) Find
objects of the approximate size for each planet (supplied by the instructor).
If the Sun was the size of a tennis ball then 0. 1 A.U. would be about 70 cm (0.7 meters) or about one
average step. Rather than measure the orbit distances with a ruler you should "pace" the distance off.
(Count how many of your steps it takes to pace off 10 meters, marked on the floor of the classroom with
a measuring tape)
Now you and your partners should go outside and build your own solar system, placing a tennis ball
labeled "Sun" at the chime tower and each team member pacing off the distance to their planet, where
they stand with their card and model object. We will construct our model outside in the center quad,
starting at the chime tower (giant fountain pen) and extending down the center toward McGloughlin
Blvd.
Questions:
1.
Look in your text for pictures of each planet. Write a short one or two word description of
each. But you can't use the same words twice! The word should not apply to all planets,
like round or spherical!
Mercury
Venus
Earth
Mars
Jupiter
Saturn
Uranus
Neptune
Pluto
2. How many times larger is Jupiter's diameter than the Earth's?
3. The volume of a planet is proportional to it's diameter cubed (D3). Take the result of question 2
and cube it to see how many Earth's would fit inside of Jupiter.
4. Use a similar calculation to find how many Earth's would fit inside the Sun.
5.
A jet airplane typically travels at a speed of about 600 miles per hour, how long would it
take, if possible, to fly from the: (a) Sun to the Earth? (Use the actual, not scale, distance.) Give
your answers in years. (b) The Sun to Pluto? Give your answers in years.
Hint: First find the distance in miles by multiplying the distance in A.U. by 93,000,000. Time in
hours is the distance in milesdivided by the speed in mph, the time in years is the time in hours
divided by both 24 and then 365.
Sun to Earth ______________
Sun to Pluto ______________
6.
The star nearest to our Sun is Alpha Centauri, which is 4.3 light years away. A light year
is the distance that light travels in one year. 1 light year is about 9,500,000,000,000 kilometers.
How many astronomical units is it to Alpha Centauri? ____________
On the scale of the model we built in part three (1AU = 7m), about how far would you have
to walk to put a second tennis ball the right distance away from the sun, to stand for Alpha
Centauri? Give your answer in kilometers: _____________________
For purposes of comparison, it is about 15 km from Clark College to downtown Portland and
about 230 km from Vancouver to Seattle and around 1600 km from Vancouver to San Diego.